01 분류 문제
회귀, 분류
분류는 정해진 값 중 예측. 회귀는 연속적이 값 예측.
예컨대 집 값을 예측하는 것은 회귀 문제이지만 이 이메일이 스펨메일인지 아닌지는 분류 문제이다. 그러나 분류 문제도 다음과 같이 선형 회귀로 나타낼 수 있기는 하다.
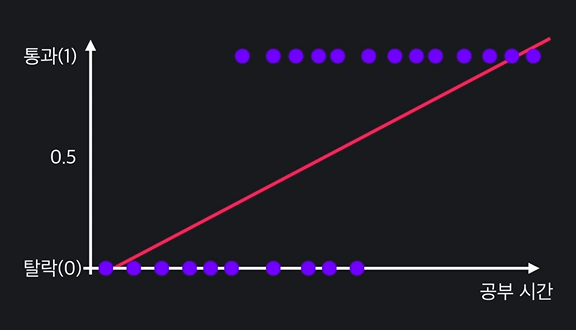
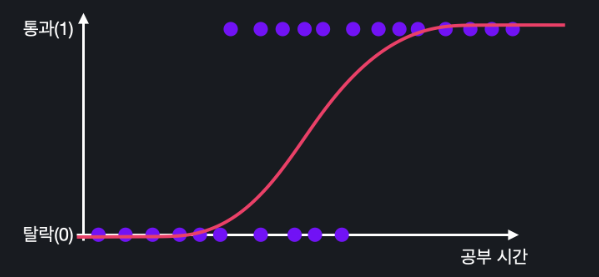
0과 1로 아예 나누고, 선을 그어 다음 데이터에 대해 판단하면 되기 때문이다. 그러나 선형 회귀는 특정 아웃라이어에 대해 민감하게 반응하기 때문에 분류로 사용하지 않는다. 지금 이 그래프에서도 만약 공부 시간이 특출난 데이터가 있다면 그래프 자체의 기울기가 변하면서 다음데이터에 대한 예측이 변한다.
02 분류 문제 노트
03 로지스틱 회귀
Logistic Regression
분류 문제를 풀기 위한 회귀.
로지스틱은 데이터에 가장 잘 맞는 시그모이드 함수를 찾는다.
식과 그래프는 다음과 같다.
✅ 시그모이드 함수
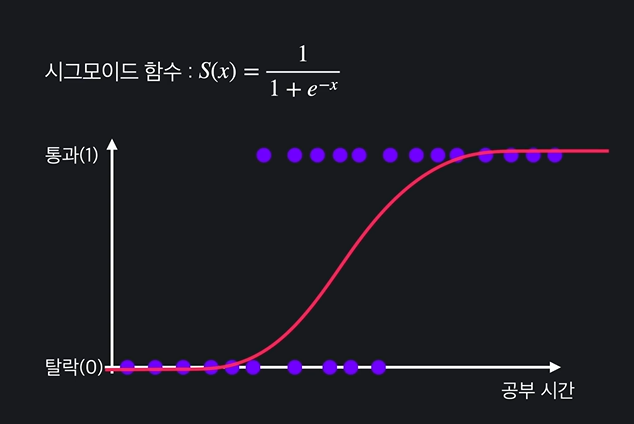
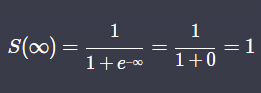
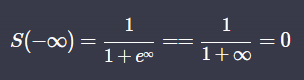
- 무조건 0과 1 사이에서 움직인다.
- x가 클수록 1, 작을수록 0에 가까워진다.
- 따라서 분류를 할 때 유용하게 사용할 수 있다
- 데이터 하나에 민감하게 반응하는 문제를 해결한다
그런데 왜 분류를 하는 함수를 회귀라 부를까?
결국 로지스틱 회귀함수 S(x) 의 값도 연속적(=회귀)이기 때문이다.
그러나 그러한 특성 외에 0과 1 사이 값으로 로지스틱은 분류하기에 적합하며, 각 실수 값이 0.5보다 큰지 작은지를 기준으로 분류**한다.
04 로지스틱 회귀 노트
05 로지스틱 회귀 가설 함수
가설함수 : 입력 변수를 받아 목표 변수를 예측해주는 변수.
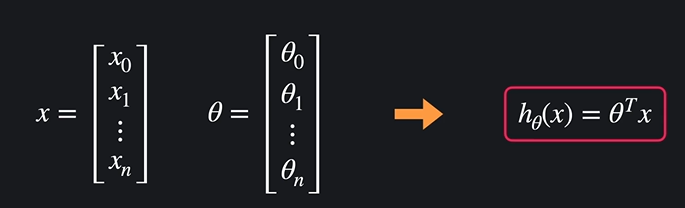
빨간 박스와 같이 간결하게 표현하는 것이 가능하다.
다음 빨간 박스의 아웃풋 (세타.T와 X의 곱)을 시그모이드 함수 안에 대입한다.
이렇게 대입하는 이유는 아웃풋을 어떻게든 0과 1사이의 값으로 만들어주기 위함이다.
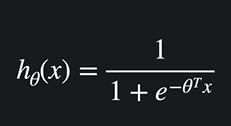
다음과 같은 함수가 된다!
x를 잘 넣고, 나온 값을 그래프에 표시하고, 값이 0.5가 넘으면 통과, 못넘으면 탈락과 같은 방법으로 분류하면 된다.
06 로지스틱 회귀 가설 함수 노트
07 로지스틱 회귀에서 하려는 것
다음과 같은 로지스틱 회귀의 가설함수는 실제로 어떤 의미일까?
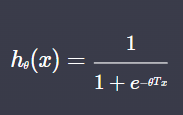
(e 위의 지수는 -(선형 회귀 가설함수)이다.)
결국 로지스틱 회귀의 가설함수 또한 주어진 데이터에 가장 잘 맞는 함수를 찾는 것이고, 이것은 세타값 2개의 조절을 통해 완성된다.
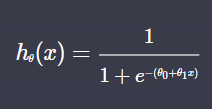
위의 함수에서 세타.T 와 X의 곱을 펼치면 다음과 같다.
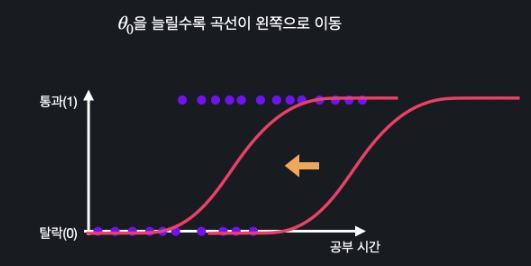
✅ 세타0의 영향
세타0이 늘어날수록 곡선이 왼쪽으로 움직인다.
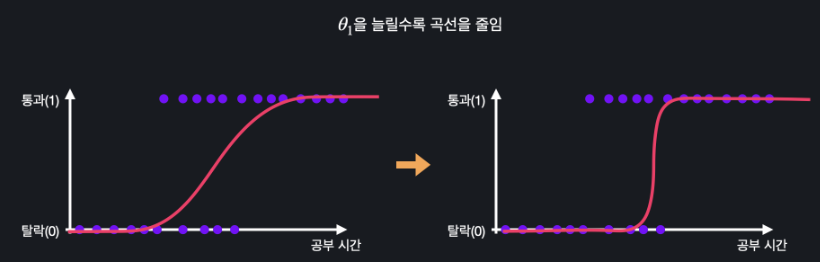
✅ 세타1의 영향
세타1이 늘어날수록 곡선의 모양이 조여진다.
결국 두 개의 값을 데이터에 맞게 가장 잘 조절하는 것이 로지스틱 회귀, 분류의 목적이다.