01 다항 회귀
이전에 학습했던 선형 회귀는 직전의 가설 함수를 가진다. (x의 차수가 1)
그러나 이렇게 데이터를 예측한다고 해서 항상 정확한 것은 아니다.
오히려 데이터의 분포에 맞게 가설 함수를 곡선으로 구성하는 것이 데이터에 더 잘 맞는 예측선일 수 있다.
이처럼 가설 함수를 일차식이 아닌 다항 함수로 구성하는 것을 다항 회귀, Polynomial Regression 이라고 한다.
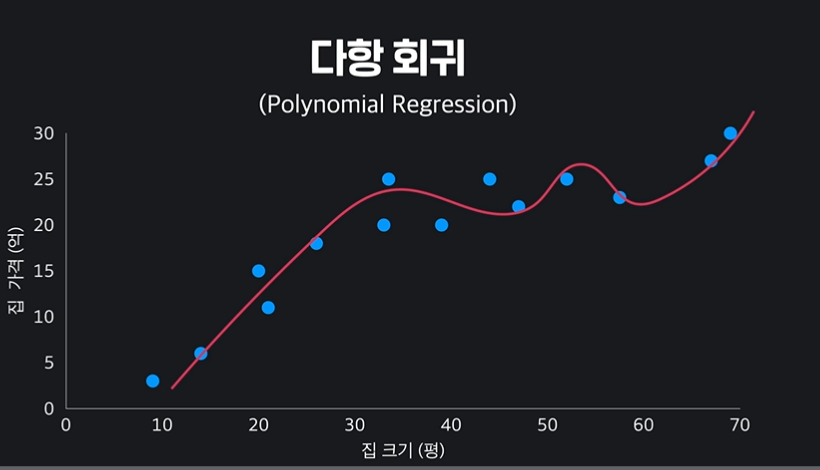
02 다항 회귀 노트
03 단일 속성 다항 회귀
회귀에는 속성이 여러 개인 것과 속성이 1개인 것이 있다. 지금은 속성이 하나인 것만 보자.
선형 회귀에서 중요한 것은 일차식의 파라미터와 상수항, 즉 세타 값의 최적값을 찾는 것이었다. (손실이 최소가 되도록 업데이트)
역시나 다항회귀에서도 마찬가지다. x의 차수가 올라가더라도, 세타값들의 최적값만 찾으면 된다. 사진을 보자.
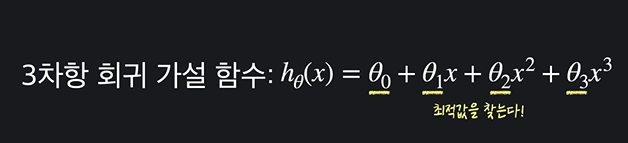
그런데 이러한 다항 회귀함수는 선형 회귀 중 다중 선형과 굉장히 비슷해보인다.
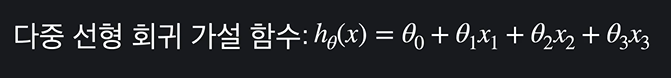
나머지 x 가 제곱, 세제곱만 된 것이 다항 회귀 함수이며, 예를 들면 다음과 같다.
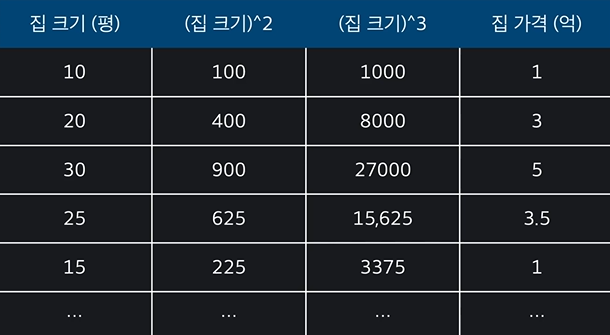
앞에 세타를 제외하고 입력변수 x 만 보자. 선형 회귀는 무조건 집 크기가 들어가지만, 다항 회귀는 집크기^2, 집크기^3 이 된다. 그것 외에 차이는 없다!
입력 변수가 하나인 다항 회귀는 다중 선형 회귀에서 x의 차수만 늘린 것이다.
04 단일 속성 다항 회귀 노트
05 다중 다항 회귀
입력 변수 3개, 목표 변수 1개인 다중 다항 회귀 상황을 보자.
각각의 입력변수를 x1, x2, x3, 라 하자.

입력변수가 3개이고, 가설함수를 2차함수라고 해야할 때,
(상수항 + 일차항 + 이차항, 이차항은 x1^2 도 이차항이지만 x1x2 도 이차항이다.)
가능한 이차항은 다음과 같다.

최종적으로 식은 다음과 같다.
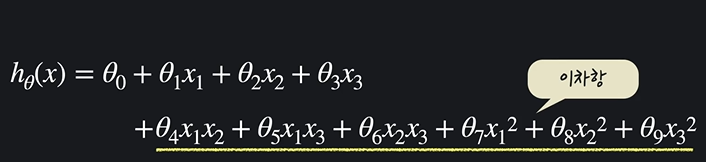
그러면 어떻게 생각해야 할까? 이를 다중 선형 회귀의 관점에서 보면 입력변수는 총 9개다.
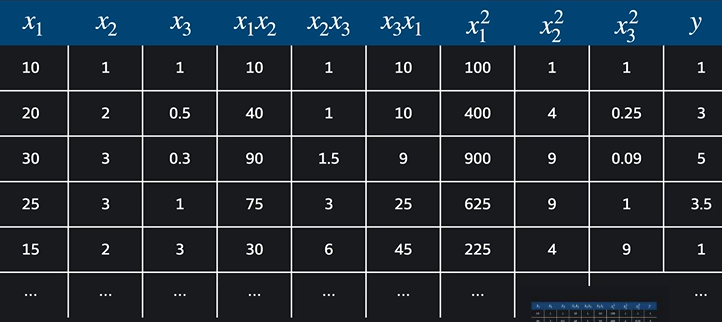
일차항 3개와 이차항 6개가 잘 들어갔다.
따라서 입력변수 여러 개인 다중 다항 회귀 역시 입력 변수가 많은 다중 선형 회귀이다.
06 다중 다항 회귀 노트
07 다항 회귀의 힘
다항 회귀는 왜 사용하는 것일까?
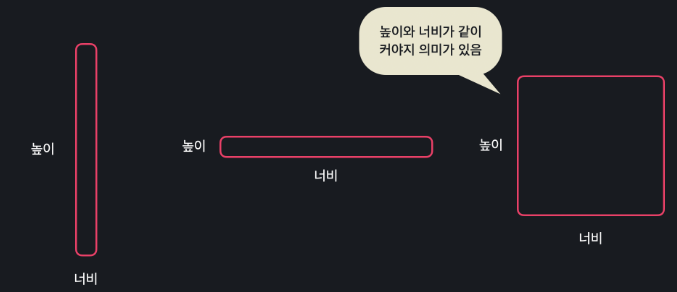
단순 선형 회귀를 사용하면 높이와 넓이 변수가 서로 독립적이므로 (입력 변수끼리 곱해지지 않음) 위와 같은 상황에서 "높이와 너비가 같이 커야지만 집 값도 커진다" 라는 관계를 학습할 수 없다.
높이 > 집 값, 너비 > 집 값 관계만 찾는 것이다.
그러나 다항 회귀는 높이 * 너비 데이터도 사용함으로서 속성들 사이에 있을 수 있는 복잡한 관계들을 프로그램에 학습시킬 수 있다.
08 scikit-learn 으로 다항 회귀 문제 만들기
다항회귀를 준비하는 방법은 다음과 같다.
✅ 라이브러리
from sklearn.datasets import load_boston
from sklearn.preprocessing import PolynomialFeatures
import pandas as pd
boston_dataset = load_boston()✅ .shape 와 .feature_names 로 확인
boston_dataset 에는 506행 13열 짜리의 집 값 데이터가 들어가 있다.
.feature_names 는 열 이름을 확인할 수 있는 메서드다.

✅ PolynomialFeatures() 로 다항식 생성
PolynomialFeatures() 안에 정수를 써넣게 되면 해당 차수의 식이 만들어진다. 이차식을 만들어보자.
polynomial_transformer = PolynomialFeatures(2)
polynomial_data = polynomial_transformer.fit_transform(boston_dataset.data)
polynomial_data트랜스포머 변수는 이제 다항변형기로 다항 회귀를 위해 데이터를 가공할 수 있다.
.fit_transform 안에 우리 데이터를 넣어준다.
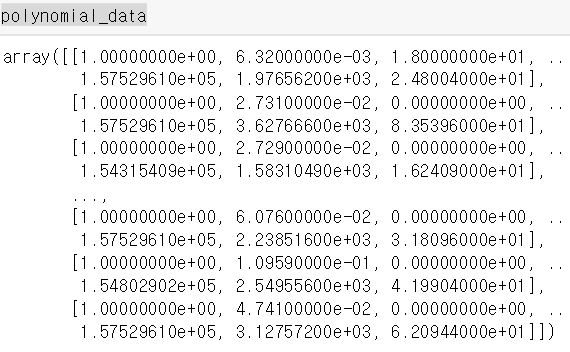
역시나 .shape 을 찍어보자.
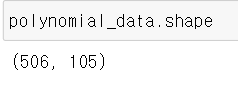
13개였던 열이 105개가 되었다. 항들끼리 서로 곱해지면서 다차항을 만들었기 때문이다.
get_feature_names 안에 데이터 이름들을 넣어보자.
polynomial_feature_names = polynomial_transformer.get_feature_names(boston_dataset.feature_names)
polynomial_feature_names
105개의 수많은 열이 확인된다.
이를 열로 삼아 데이터 프레임을 만들자.
X = pd.DataFrame(polynomial_data, columns = polynomial_feature_names)import pandas as pd
X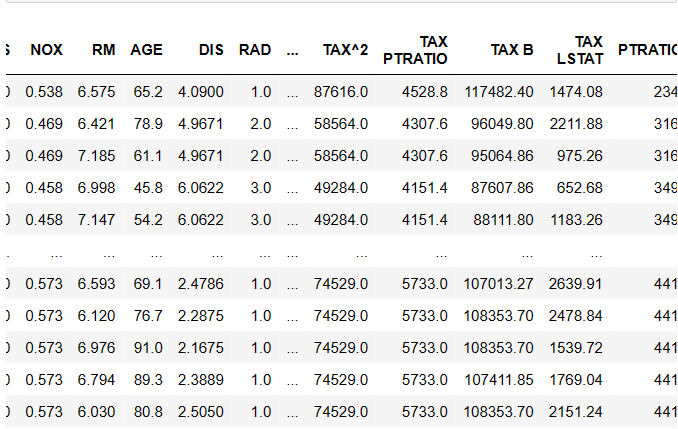
09 사이킷런으로 다항 회귀 구현
✅ 목표변수 y 도 데이터프레임으로 저장하기
y = pd.DataFrame(boston_dataset.target, columns = ["MEDV"])MEDV 는 해당 자료에서 집값에 해당하는 목표변수이다.

✅ 모듈 불러오기 (합쳐서 정리)
from sklearn.datasets import load_boston
from sklearn.preprocessing import PolynomialFeatures
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error정리
train_test_split : 트레인변수와 테스트 변수 분리
LinearRegression : 모델 만드는
mean_squared_error : 평균 제곱 오차 (근을 위해선 0.5)
코드
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2, random_state = 5)
model = LinearRegression() #선형 회귀 모델
model.fit(X_train, y_train) #학습시키기
model.coef_ #세타값
model.intercept_ #세타0분리하고 > 모델 만들고 > 만든 모델로 학습 > 세타값들 출력

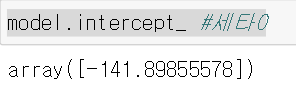
y_test_prediction = model.predict(X_test) #모델의 예측값
mean_squared_error(y_test, y_test_prediction) ** 0.5 #에측값과 실제 아웃풋 괴리
#test의 실제 아웃풋, 예측된 아웃풋. 그것의 평균제곱근 오차. 3.196527651588392
모델로 테스트 예측 > 실제 아웃풋(점들)과 모델 예측(이차곡선)의 차이 확인.
차이가 지금까지 학습한 모델 중 가장 적었던 것을 확인했다!
10 다항 회귀로 당뇨병 예측하기
from sklearn import datasets
from sklearn.preprocessing import PolynomialFeatures
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
import pandas as pd
# 여기에 코드를 작성하세요
diabetes_dataset = datasets.load_diabetes() # 데이터 셋 갖고오기
polynomial_transformer = PolynomialFeatures(2)
polynomial_data = polynomial_transformer.fit_transform(diabetes_dataset.data)
polynomial_feature_names = polynomial_transformer.get_feature_names(diabetes_dataset.feature_names)
X = pd.DataFrame(polynomial_data, columns = polynomial_feature_names)
# 테스트 코드
X.head()다항변환기와 프레임 코드 사이 2줄을 잘 보자! 그것 말고는 없다.
11 다항 회귀로 당뇨병 예측하기 (2) 학습시키기
# 목표 변수
y = pd.DataFrame(diabetes_dataset.target, columns=['diabetes'])
# 여기에 코드를 작성하세요
X_train, X_test , y_train, y_test = train_test_split(X, y, test_size = 0.2, random_state= 5)
model = LinearRegression()
model.fit(X_train, y_train)
y_test_predict = model.predict(X_test)
mse = mean_squared_error(y_test, y_test_predict)
mse ** 0.5X_train, X_test, y ... 등의 순서가 바뀌지 않도록 주의하자.