01 함수
수학 에서의 함수
input을 받고output을 돌려주는 것.
y = 3x + 6
하나의 인풋에 대해서 하나의 아웃풋만.
-고차 함수: 고차 함수로 올라갈 수 있음
-다변수 함수: 인풋이 여러 개일 수 있음. f(x,y) = x + 2y
- d(거리) = 60t(시간)
- BMI = 몸무게 / 키 * 키
02 그래프
수학 식을 시각적으로 표현하는 방법
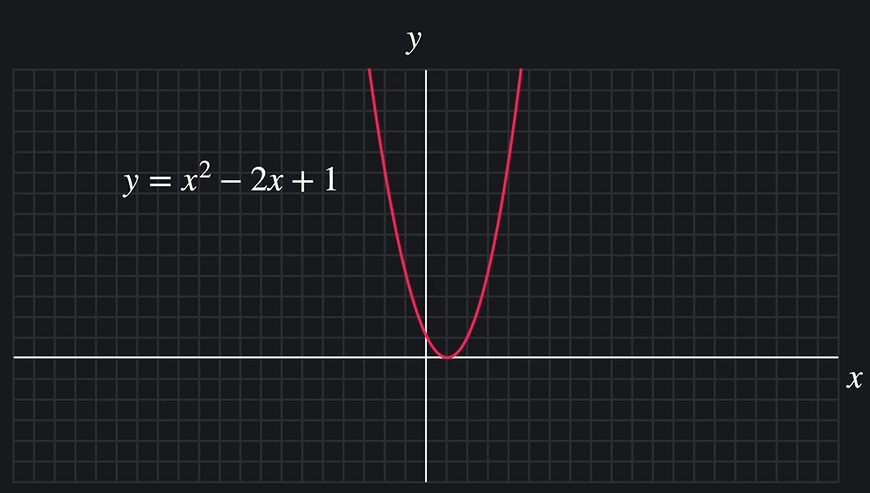
그래프를 그리는 이유 : 함수의 다양한 특징을 시각적으로 확인하기 위함.
머신러닝 역시 그래프의 도움이 필요!
03 평균 변화율
y = 2x + 1
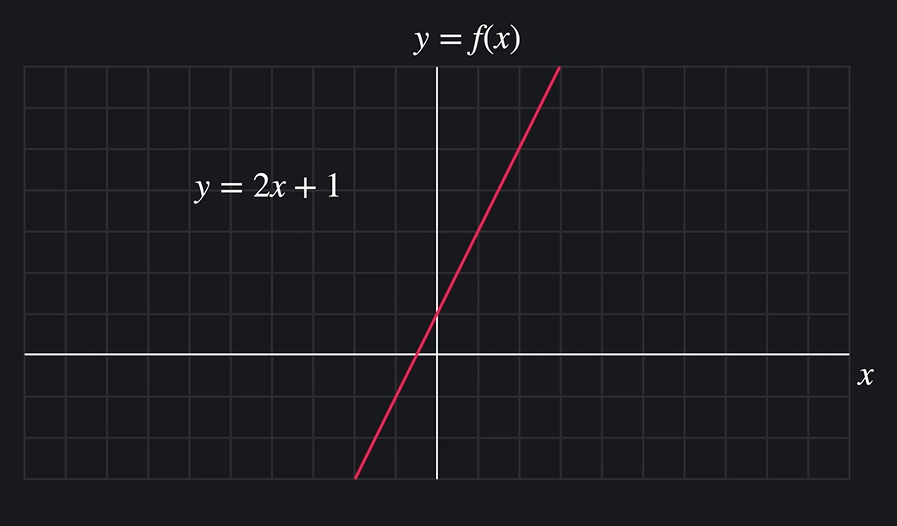
y = x^2 -2x + 1
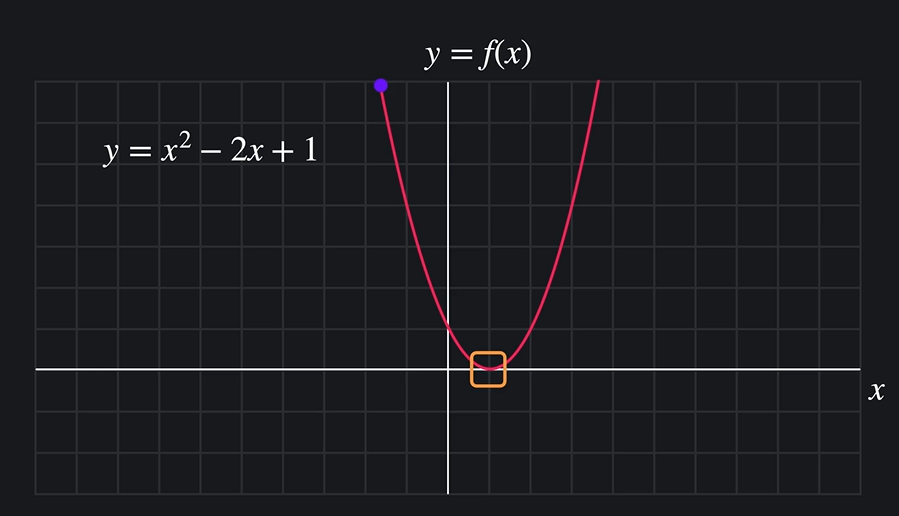
기울기: x 가 변화할 때 y는 얼마나 빠르게 변하는지
첫 사진에서 그래프는 어떤 지점에서든지 기울기는 2이다.
두 번째 사진에서는 순간 변화율 의 계산이 필요.
평균변화율
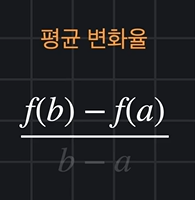
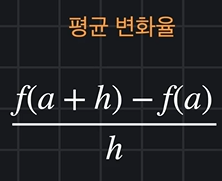
04 순간 변화율
✅ 순간변화율은 평균변화율의 극한이다.
직선이 아닌 함수는 위치에 따라 기울기가 다르다.
x = 2 일 때 y = x^2 -2x + 1 의 순간변화율

리미트 h 는 0으로 간다
05 미분
✅ 미분은 순간변화율의 일반화된 형태이다.
**함수 f(x) = x^2 -2x + 1 미분해보기

f'(x) 로 표기한다(미분)
a 가 x 로 일반화되었다.
06 미분 노트
07 가장 가파른 방향 (2차원)
기울기는 해당 지점에서 얼마나 기울어져 있는지 도 알려주지만,
어떤 방향으로 가야 가장 가파르게 올라갈 수 있는지 도 알려준다.
08 가장 가파른 방향 노트
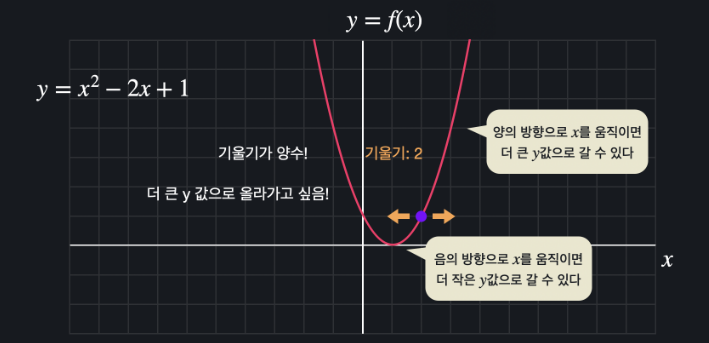
예를 들어 기울기가 -2라는 건, 왼쪽으로 움직이면 더 큰 y 값으로 올라가고, 오른쪽으로 움직이면 y 값이 감소하는 지점이라는 뜻이다.
반대로 기울기가 2라는 건, 오른쪽으로 움직여야 가파르게 올라가고, 왼쪽으로 움직이면 작아진다는 뜻이다.
09 극소점 극대점
순간변화율이 0이라는 것은 x가 변해도 y가 그대로라는 것.
- ✅ 극소점 : 기울기가 음수에서 양수로 전환할 때. (극소가 최소점인 것은 아님)
_ ✅ 극대점 : 왼쪽으로는 기울기 양수, 오른쪽으로는 음수.(극대가 최대점인 것은 아님)
- ✅ 안장점: 기울기는 계속 양수인데 0을 찍고 다시 가팔라지는 경우.
10 극소점, 극대점 노트
11 고차원에서 미분
input 변수가 두 개일때.
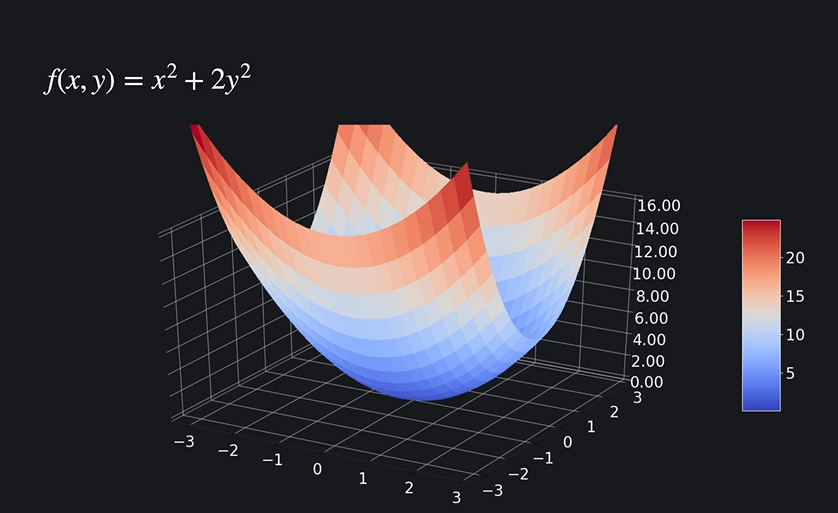
위의 함수와 같을 때 편미분이 필요하다.
편미분 : 변수를 하나에 관해서만 미분. (델 이라고 읽음)
x에 대해 미분: 나머지는 상수 취급
델f(x,y) = 2x
y에 대해 미분: 나머지는 상수 취급
델f(x,y) = 4y
두 결과를 벡터로 나타내어 기울기 를 표현하고, 역세모로 표현한다.

만약 x,y 특정 지점에서 기울기를 알고 싶으면 위 벡터에 대입을 하면된다.
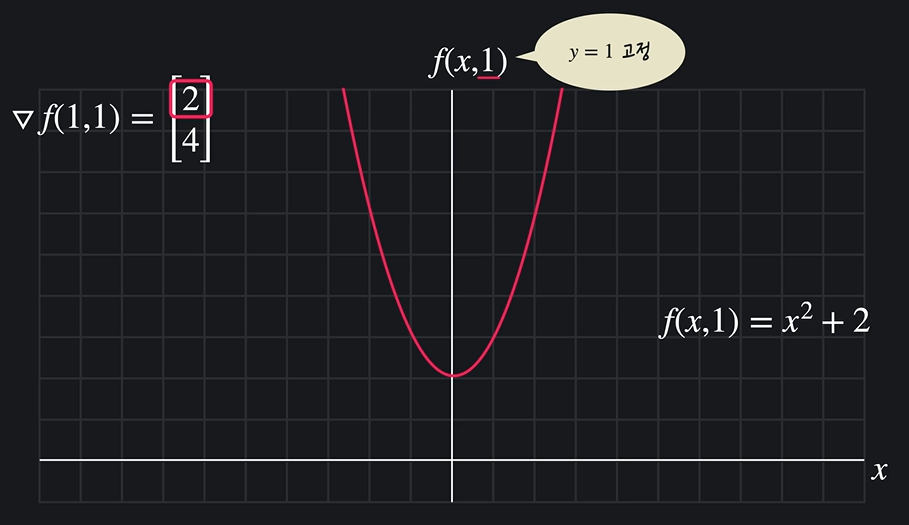
x = 1, y = 1 을 대입하면 기울기가 벡터 2, 4 이다. 무슨 의미일까?
2의 의미
y = 1로 고정되어 있고, f(x, 1) = x^2 + 2
x = 1 일 때의 함수 f 의 기울기는 2
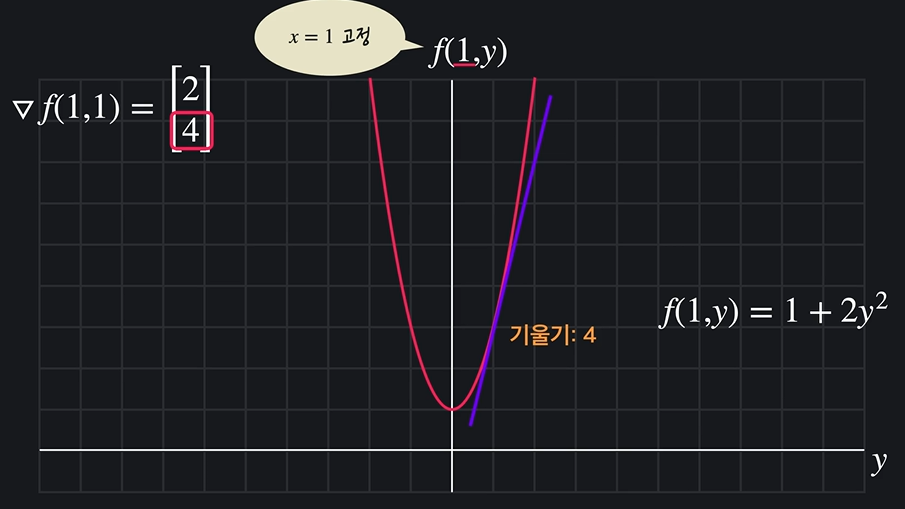
4의 의미
x = 1이 고정되어 있고, f(1,y) = 1 + 2y^2
y = 1일때 함수 f 기울기는 4.
12 고차원에서의 미분
13 가장 가파른 방향 (고차원)
가장 가파르게 올라가는 방법 (기울기 벡터에 대입 한 방향)
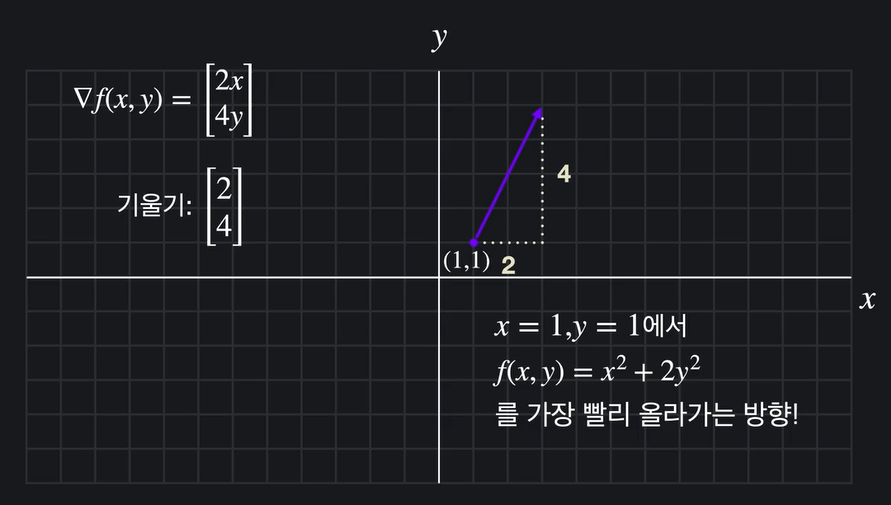
x = 1, y = 1 에서 가장 가파르게 올라가는 방법은 숫자를 대입한 벡터 2, 4만큼 좌표에서 움직인 방향이다.
가장 가파르게 내려가는 방법 (기울기 벡터에 -1 곱한 방향)
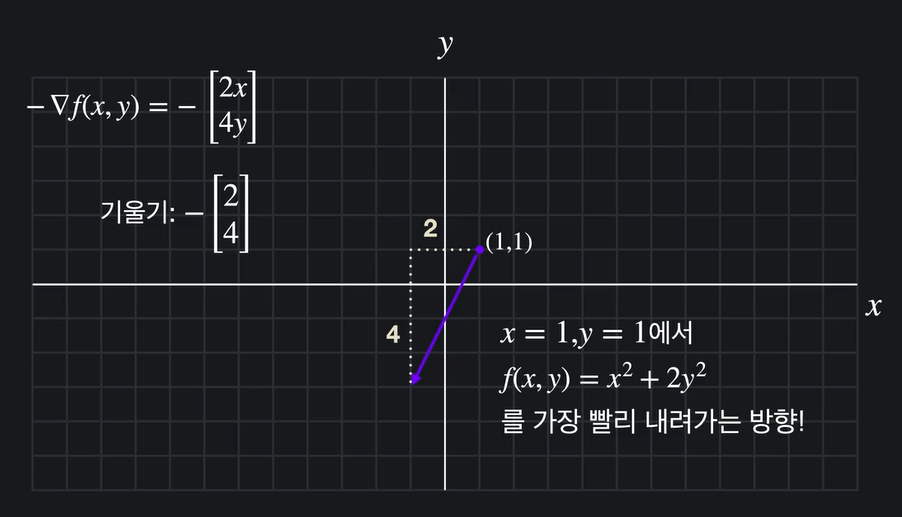
가장 가파르게 내려가는 방법은 벡터에 일단 -1 을 스칼라곱, 그 후에 좌표를 대입한 방향으로 이동하는 것이다.
input이 3개 이상이면 시각적으로 이해하기 힘듦.
🎈편미분 > 기울기 벡터 > 함수에서 가장 가파르게 올라가는 방향
을 기억하자.
편미분을 하고 둘을 수합하면 기울기 벡터를 만들 수 있고, 해당 좌표를 대입한 방향이 가파르게 올라가는 / 내려가는 방향이다.
14 가장 가파른 방향 노트
15 머신 러닝에 미분이 필요한 이유
순간변화율 = 그 점에서의 기울기 (극소, 극대, 어디서 증가? 감소?)
머신러닝 모델의 성능 평가, 최적화 에 사용된다.
f(x) = x^2 -2x - 3 의 복잡도.
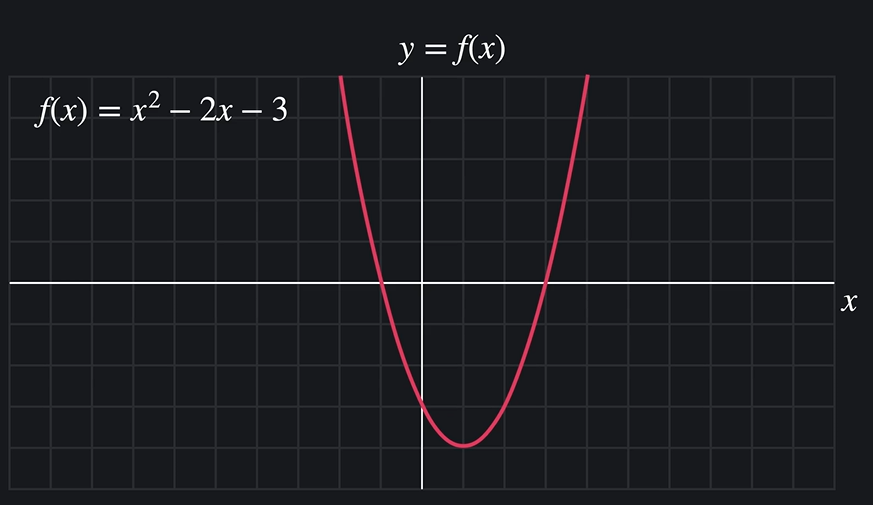
x = 1 에서 최적화 할 수 있다.
머신러닝 모델의 최적화에서 함수의 극대, 극소를 찾아야 하므로 미분 개념이 필요한 것.