지난 포스팅에 이어서 행렬을 더 다뤄보자.
13 numpy 로 행렬 연산하기
일반 덧셈은
스칼라 곱은
행렬 간 곱은 @ 을 사용한다.
import numpy as np
A = np.array([
[1,-1,2],
[3,2,2],
[4,1,2]
])
B = np.random.rand(3,3)A + B
5 * A
A @ Barray([[ 1.0577951 , -0.13165319, 2.35157507],
[ 3.97207041, 2.27187225, 2.98398792],
[ 4.39755681, 1.68019447, 2.49748949]])
array([[ 5, -5, 10],
[15, 10, 10],
[20, 5, 10]])
array([[-0.1191617 , 1.95686351, 0.36256612],
[ 2.91263975, 4.50917388, 4.01768005],
[ 1.99836444, 5.10564845, 3.3852672 ]])행렬의 곱은 * 이 아닌 @ 임에 유의하자. np.dot(A,B) 로도 계산할 수 있다.
14. numpy 로 행렬 연산 연습하기
15. 전치행렬, 단위행렬, 역행렬
✅ 전치행렬 (Transposed matrix)
A의 행렬의 열과 행을 바꾼 행렬 을 뜻한다. T를 써서 표기한다.
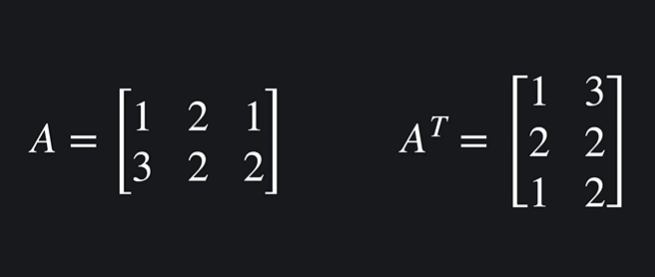
행렬의 모양을 맞추기 위해 사용한다.
✅ 단위 행렬 (identity matrix)
어떤 행렬과 곱하여 기존 행렬 유지를 만드는 행렬 이다.
정사각형 모양이며, 왼쪽에서 오른쪽 대각선으로 1을 채우고 나머지는 0으로 채운다.
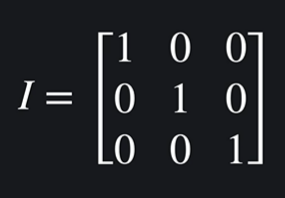
이 행렬과 어떤 행렬을 곱해도 그 어떤 행렬의 기존 값이 유지된다.
3 X 3 뿐 아니라 정사각형 어떤 모양이라도 규칙만 지키면 단위행렬이라 할 수 있다.
✅ 역행렬
특정 A 행렬과 곱했을 때 단위행렬이 나오는 행렬이다.
- 역행렬 역시 정사각형이다.
- 모든 행렬이 역행렬을 가지는 것은 아니다. (어떤 것을 곱해도 단위행렬이 나오지 않는 행렬이 있다.)
16 전치행렬, 단위행렬, 역행렬 노트
17 numpy 로 전치, 단위, 역행렬 연습
array([[ 1, -1, 2],
[ 3, 2, 2],
[ 4, 1, 2]])
주어진 A 행렬에서 전치, 단위, 역행렬을 코드로 작성해보자.
전치행렬 코드
np.transpose(A)
array([[ 1, 3, 4],
[-1, 2, 1],
[ 2, 2, 2]])행과 열이 뒤바뀌었다.
단위행렬 코드
I = np.identity(3)
A @ I
array([[ 1., -1., 2.],
[ 3., 2., 2.],
[ 4., 1., 2.]])단위행렬 I 를 생성하고 기존 행렬 A 와 곱했더니 A 와 일치하는 행렬이 나왔다.
역행렬 코드
A_inverse = np.linalg.pinv(A)
A_inverse = np.linalg.pinv(A)
A @ A_inversearray([[ 1.00000000e+00, 6.66133815e-16, -1.11022302e-15],
[-2.22044605e-16, 1.00000000e+00, -6.66133815e-16],
[ 0.00000000e+00, 2.22044605e-16, 1.00000000e+00]])그런데 역행렬을 곱하면 값이 1과 0으로 잘 나와야 하는데 왜이럴까? pinv 메서드는 역행렬이 존재하지 않아도 최대한 비슷한 값을 반환하기 때문이다. 알아두자.
18 numpy 로 실습
19 선형대수학과 행렬/벡터
선형대수학은 행렬, 벡터, 일차식, 일차함수의 개념을 모두 포함한다.
그런데 일차식, 함수와 벡터/행렬 사이 관계는 무엇인가?
왼쪽의 일차식들이 모여있는 것을 선형 시스템 이라고 한다.
그런데 복잡해 보이는 선형 시스템을 행렬 사이의 곱으로 오른쪽 같이 표현할 수 있다.
(실제로 곱하면 같다.)
이처럼 아무리 복잡한 일차식이어도 행렬/벡터로 간단히 표현할 수 있다 는 게 선형대수학이 바라보는 목표이다.
20 선형대수학이 머신러닝에 필요한 이유
21 선형대수학 실습
