15 선형 회귀 가설 함수 구현하기
import numpy as np
def prediction(theta_0, theta_1, x):
"""주어진 학습 데이터 벡터 x에 대해서 예측 값을 리턴하는 함수"""
# 여기에 코드를 작성하세요
result = theta_0 + theta_1 * x
return result
# 테스트 코드
# 입력 변수(집 크기) 초기화 (모든 집 평수 데이터를 1/10 크기로 줄임)
house_size = np.array([0.9, 1.4, 2, 2.1, 2.6, 3.3, 3.35, 3.9, 4.4, 4.7, 5.2, 5.75, 6.7, 6.9])
theta_0 = -3
theta_1 = 2
prediction(theta_0, theta_1, house_size)
딱히 생각하고 넘어갈 부분이 없다.
16. 선형 회귀 예측 오차 구현하기
import numpy as np
def prediction(theta_0, theta_1, x):
"""주어진 학습 데이터 벡터 x에 대해서 모든 예측 값을 벡터로 리턴하는 함수"""
# 지난 실습의 코드를 여기에 붙여 넣으세요
def prediction_difference(theta_0, theta_1, x, y):
"""모든 예측 값들과 목표 변수들의 오차를 벡터로 리턴해주는 함수"""
return prediction(theta_0, theta_1, x) - y
# 입력 변수(집 크기) 초기화 (모든 집 평수 데이터를 1/10 크기로 줄임)
house_size = np.array([0.9, 1.4, 2, 2.1, 2.6, 3.3, 3.35, 3.9, 4.4, 4.7, 5.2, 5.75, 6.7, 6.9])
# 목표 변수(집 가격) 초기화 (모든 집 값 데이터를 1/10 크기로 줄임)
house_price = np.array([0.3, 0.75, 0.45, 1.1, 1.45, 0.9, 1.8, 0.9, 1.5, 2.2, 1.75, 2.3, 2.49, 2.6])
theta_0 = -3
theta_1 = 2
prediction_difference(-3, 2, house_size, house_price)예측오차를 구현하면 위과 같다.
17. 선형 회귀 경사 하강법 구현하기
import numpy as np
def prediction(theta_0, theta_1, x):
"""주어진 학습 데이터 벡터 x에 대해서 모든 예측 값을 벡터로 리턴하는 함수"""
# 지난 실습의 코드를 여기에 붙여 넣으세요
result = theta_0 + theta_1 * x
return result
def prediction_difference(theta_0, theta_1, x, y):
"""모든 예측 값들과 목표 변수들의 오차를 벡터로 리턴해주는 함수"""
return prediction(theta_0, theta_1, x) - y
def gradient_descent(theta_0, theta_1, x, y, iterations, alpha):
"""주어진 theta_0, theta_1 변수들을 경사 하강를 하면서 업데이트 해주는 함수"""
for _ in range(iterations): # 정해진 번만큼 경사 하강을 한다
error = prediction_difference(theta_0, theta_1, x, y) # 예측값들과 입력 변수들의 오차를 계산
# 여기에 코드를 작성하세요
theta_0 = theta_0 - alpha * error.mean()
theta_1 = theta_1 - alpha * (error * x).mean()
return theta_0, theta_1
# 입력 변수(집 크기) 초기화 (모든 집 평수 데이터를 1/10 크기로 줄임)
house_size = np.array([0.9, 1.4, 2, 2.1, 2.6, 3.3, 3.35, 3.9, 4.4, 4.7, 5.2, 5.75, 6.7, 6.9])
# 목표 변수(집 가격) 초기화 (모든 집 값 데이터를 1/10 크기로 줄임)
house_price = np.array([0.3, 0.75, 0.45, 1.1, 1.45, 0.9, 1.8, 0.9, 1.5, 2.2, 1.75, 2.3, 2.49, 2.6])
# theta 값들 초기화 (아무 값이나 시작함)
theta_0 = 2.5
theta_1 = 0
# 학습률 0.1로 200번 경사 하강
theta_0, theta_1 = gradient_descent(theta_0, theta_1, house_size, house_price, 200, 0.1)
theta_0, theta_1경사 하강법을 코드로 구현하면 다음과 같다.
18 경사 하강법 구현 시각화
경사하강법 구현을 시각화하기 위해선 손실함수를 계산하여 다음과 같이 gradient_descent 함수를 고쳐본다.
def gradient_descent(theta_0, theta_1, x, y, iterations, alpha):
m = len(x)
cost_list = []
"""주어진 theta_0, theta_1 변수들을 경사 하강를 하면서 업데이트 해주는 함수"""
for i in range(iterations): # 정해진 번만큼 경사 하강을 한다
error = prediction_difference(theta_0, theta_1, x, y) # 예측값들과 입력 변수들의 오차를 계산
# 여기에 코드를 작성하세요
cost = error@error / 2*m
cost_list.append(cost)
theta_0 = theta_0 - alpha * error.mean()
theta_1 = theta_1 - alpha * (error * x).mean()
if i % 10 ==0:
plt.scatter(house_size, house_price)
plt.plot(house_size, prediction(theta_0, theta_1, x), color = 'red')
plt.show()
return theta_0, theta_1, cost_list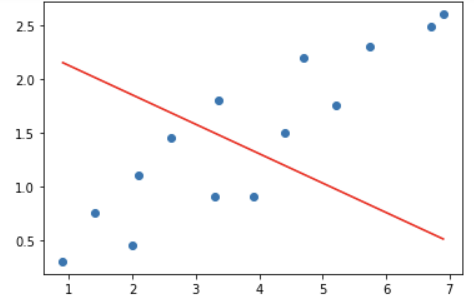
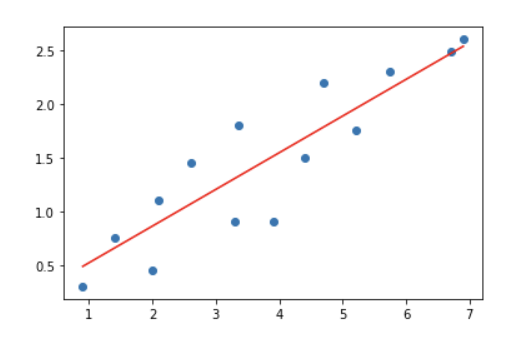
후에 gradient_descent 함수를 호출했을 때 10개의 그래프가 나왔으며, 시간이 지날수록 점점 손실이 개선되는 것을 확인할 수 있었다.
cost_list 를 출력하면 점점 줄어드는 손실을 확인할 수 있다.
19 학습률 알파
경사하강법을 한다는 것은 세타를 업데이트 한다는 것이다.
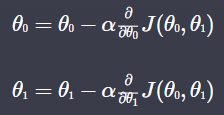
세타0에 대한 편미분, 세타1에 대한 편미분 값을 알파 에 곱하여 기존 값에서 빼는 것이 경사하강법이다.
그렇다면 알파는 어떻게 정할까?
✅ 알파가 너무 큰 경우
-알파가 너무 큰 경우에는 경사 하강법을 할 때마다 세타의 값이 너무 많이 바뀐다.
- 성큼성큼 움직인다
- 너무 크다면 오히려 손실함수 J 의 최소점에서 멀어질 수 있다
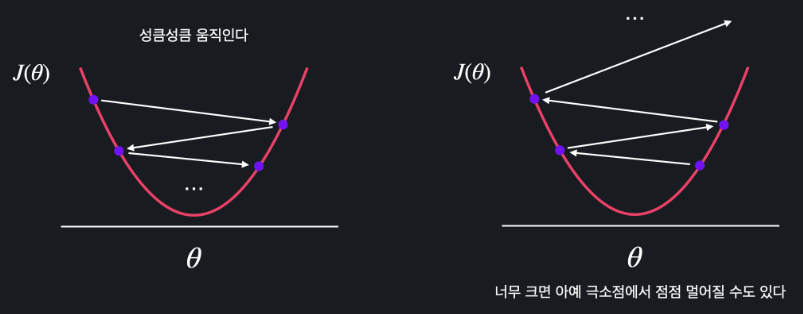
✅ 학습률 알파가 너무 작은 경우
- 너무 작게 움직인다
- 시간이 오래 걸린다
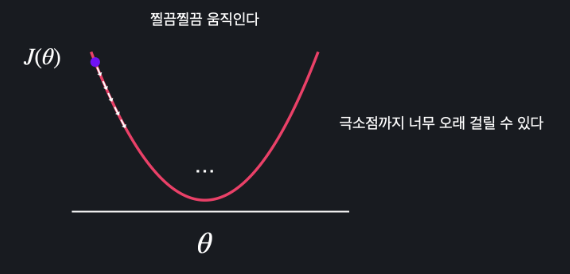
✅ 적절한 알파?
따라서 적절한 알파란 빠르고 정확하게 최소점까지 가는 학습률이다.
학습률이 너무 크면 경사 하강법을 할수록 손실 그래프가 커질 것이고,
학습률이 너무 작으면 Iteration 수가 너무 많아질 것이다.
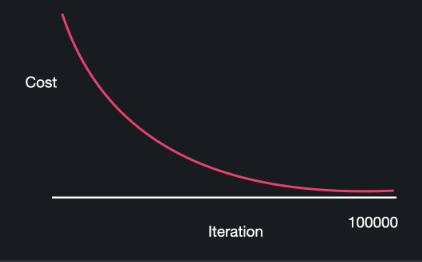
일반적으로 1.0 - 0.0 사이의 숫자를 정하고 여러개를 실험하면서 선택한다.
20 모델 평가하기
가설함수 > 최적선
가설함수 =모델: 세상에 있는 무언가를 표현하고자 하는 것.
데이터를 사용해 모델을 개선하는 것을 모델을 학습시킨다! 라고 함.
가설함수를 평가하는 방법 중 또 하나.
✅ 평균 제곱근 오차 (RMSE)
평균 제곱 오차의 루트.
본래 데이터와 원을 맞춰주기 위해서.
- 학습과 평가를 위한 데이터를 나눈다 (training set, test set)
- 학습 데이터에 가장 잘 맞는 최적선을 평가 데이터를 이용해 평균제곱근 오차를 구하고, 평가한다.
21 모델 평가하기 노트
22 scikit-learn 소개 및 데이터 준비
사이킷런은 머신러닝을 공부하는 사람들이 만든 라이브러리이자 데이터들을 모아둔 것이다.
sikit-learn 에 저장된 데이터를 통해 학습을 시켜보자. 그 전에 load_boston() 에 있느 보스턴 집값의 자료에 대해 살펴보자.
#sikit-learn
from sklearn.datasets import load_boston
boston_data = load_boston()
MEDV 가 집값이다.

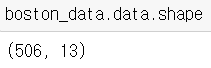
506, 13 짜리 행렬이다.
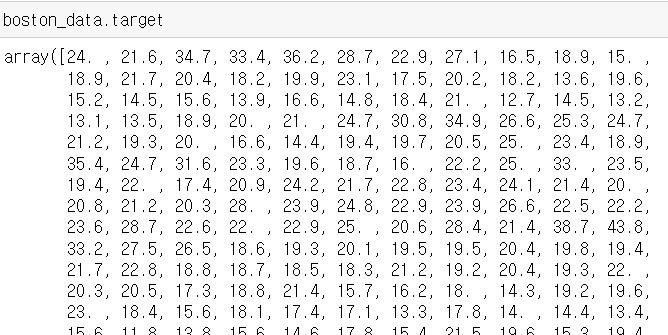
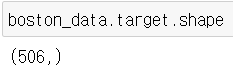
목표변수가 될 집값이다. 506짜리 벡터이다.
각각 .data 와 .target 을 x 와 y 변수로 삼아보자 (입력변수, 목표변수로 만들어보자, 데이터프레임으로!)
import pandas as pd
x = pd.DataFrame(boston_data.data, columns = boston_data.feature_names)
x = x[['AGE']]
y = pd.DataFrame(boston_data.target, columns = ['MEDV'])x에는 너무 많은 변수들이 있어 그 중 나이에 관한 열을 쓰기로 했다.
23 scikit-learn 데이터셋 나누기
우리가 함수를 평가하기 위해선 트레이닝 셋과 테스트 셋을 분리하여 따로 관리해야 한다고 했다. 이 역시 코드로 구현해주는 부분이 필요하다.
from sklearn.model_selection import train_test_split
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size = 0.2, random_state = 5)
기존 코드에 임포트 하나가 추가적으로 더 필요하다.
파라미터는 다음과 같다.
tain_test_split(입력변수, 목표변수, 테스트를 몇 퍼센트 비율로, 랜덤하게 고를 것인지 일정하게 고를것인지)
random_state 에 정수를 할당해주면 랜덤하게 고르지 않고 같은 값만 반복해서 고른다. 어떤 정수든지 상관은 없다. test_size = 0.2 라는 것은 테스트 변수의 비율을 20, 트레인 변수는 80 으로 하겠다는 것.
24 scikit-learn 으로 선형 회귀 쉽게 하기
코드는 다음과 같다.
from sklearn.linear_model import LinearRegression
model = LinearRegression()
model.fit(x_train, y_train)
model.coef_
model.intercept_
coef 는 x 앞의 계수를, intercept 는 상수를 말한다. 따라서 함수는
f(x) = 31.046174133 - -0.12402883x 와 같은 꼴이다.
model_fit 으로 선형 회귀의 함수를 찾았다면 (최적선을 찾았다면 새 데이터에 대한 예측을 해야한다. 이는 model.predict 로 한다.
y_test_prediction= model.predict(x_test)
y_test_prediction
test set 에 대한 예측값들이다.
y_test 에는 테스트들의 실제 목표값들이 들어가 있다. 평균 제곱오차(평균제곱근 오차)를 구해보자.
from sklearn.metrics import mean_squared_error
mean_squared_error(y_test, y_test_prediction)**0.5
print(y_test)8.23 이라는 숫자가 나왔다. 이는 training 셋으로 예측한 모델과 실제 값들의 오차를 뜻한다.
# 필요한 라이브러리 import
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
import pandas as pd
# 보스턴 집 데이터 갖고 오기
boston_house_dataset = datasets.load_boston()
# 입력 변수를 사용하기 편하게 pandas dataframe으로 변환
X = pd.DataFrame(boston_house_dataset.data, columns=boston_house_dataset.feature_names)
# 목표 변수를 사용하기 편하게 pandas dataframe으로 변환
y = pd.DataFrame(boston_house_dataset.target, columns=['MEDV'])
# 여기에 코드를 작성하세요
x = X[['CRIM']]
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size = 0.2, random_state = 5)
model = LinearRegression()
model.fit(x_train, y_train)
y_test_predict = model.predict(x_test)
# 테스트 코드 (평균 제곱근 오차로 모델 성능 평가)
mse = mean_squared_error(y_test, y_test_predict)
mse ** 0.5범죄율로 집값을 예측하는 코드는 다음과 같다.
하나하나 따라가면, 어렵지 않음!