다중 선형 회귀

박경민·2023년 1월 29일
0

[Machine Learning]

목록 보기
7/35

1 다중 선형 회귀

다중 선형 회귀 (Mutiple Linear Regression) 은 이전에 입력변수 하나였던 선형 회귀와 달리 입력변수를 여러개로 추가하는 것이다.
예컨대 집값을 예측하기 위해선 나이 뿐 아니라 훨씬 더 다양한 변수들이 동원된다.

다중 선형 회귀에선 세타값과 x 변수 값이 많아져 시각화를 하기가 굉장히 어렵고, 더 어렵게 느껴질 수 있으나, 사실 벡터로 이를 표현한다는 것 외에는 달라질 게 없다.

02 다중 선형 회귀 표현법

입력변수가 여러개이고 목표변수가 하나인 다중 선형 회귀는 다음과 같이 표현한다.

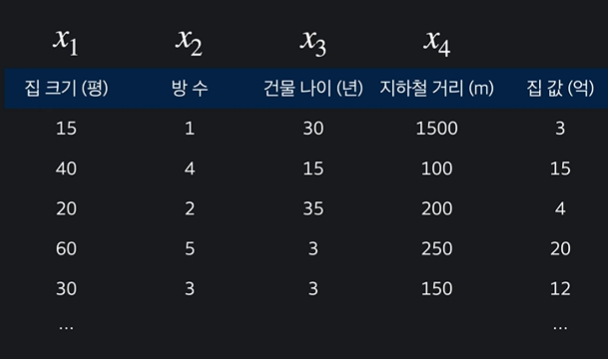
속성 여러 입력 변수를 모아 다른 말로 속성이라고 한다.
n 속성의 개수를 n 이라고 한다. 각각 x1, x2, x3, x4 이렇게 표시한다.
m 학습데이터는 하나의 행을 뜻하고, 학습 데이터의 개수를 m 이라고 한다.
벡터 위와 같은 학습 데이터들을 다음과 같이 하나로 묶어서 표현할 수 있다.

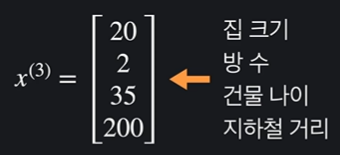
x(i) i 번째 학습 데이터이다. 괄호는 위에 표기.
x(i) j i 번째 학습 데이터의 j 번째 속성. 각각 위와 아래에 표기.

03 다중선형회귀 용어 노트

04 다중 선형 회귀 가설 함수

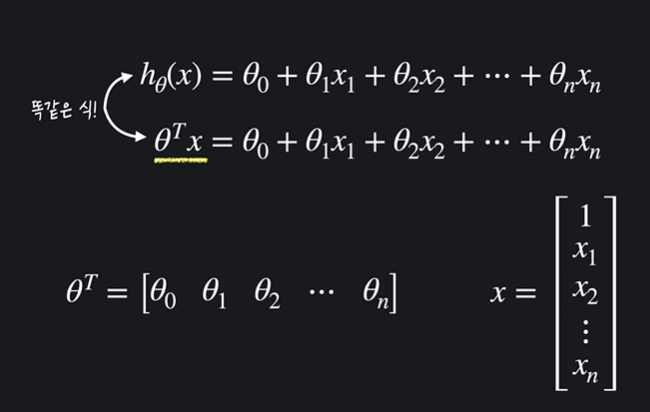
다중 선형 회귀 가설함수를 표현하는 방법은 크게 두 가지다.

✅ 기존 방법

세타0부터 n 까지와, x 변수 1부터 n까지로 사진의 위처럼 표현할 수 있다.
x 는 속성값으로, x 앞에 있는 계수는 해당 속성의 영향력 을 뜻한다.

✅ 새로운 방법

새로운 방법으로 아래와 같이 세타 벡터와 x 벡터의 곱으로 나타낼 수 있다. 벡터 사이의 곱이므로, 자리끼리 하나씩 곱하고 모두 더하면 기존 선형 회귀 식과 같다.

05 다중 선형 회귀 가설 함수노트

06 다중 선형 회귀 경사 하강법

선형회귀에서 함수들의 연결은 다음과 같다.

가설함수 : 점들을 가로지르는 함수 중 가장 정확한 것. 세타 값 두 개를 구함. (1차원 직선)
손실함수ㅕ3차원) : 오차 제곱의 평균으로 (1/2 곱) 손실함수가 작을수록 가설함수가 좋다고 할 수 있음. 이러한 손실함수를 개선하기 위해
경사하강법 : 개선하기 위해 경사하강법을 사용. 손실함수의 세타값을 업데이트 하는 것.

이렇게 정리할 수 있는데, 사실 그림으로는 다중 선형 회귀가 나타내기 어렵지만 식으로는 세타의 개수가 증가한 것을 빼곤 모두 같다.

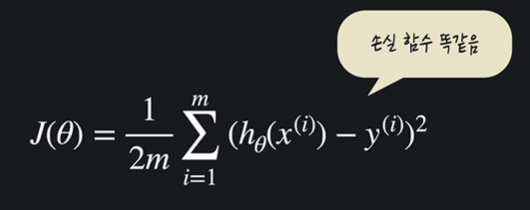
이렇게 다중 선형 회귀에서의 손실함수도 같다.

경사하강법은 어떨까? 세타 두개가 아닌 여러개를 업데이트 하는 것이다.

이를 좀 단순하게 정리하면 다음과 같다.

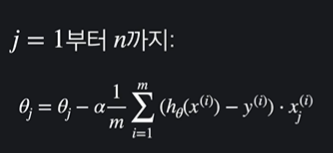
세타 값을 잘 업데이트 하면(경사하강법으로) 손실함수가 최적화되고, 이는 데이터에 가장 잘 맞는 최적선을 찾았음을 의미한다.

07 다중 선형 회귀 경사 하강법 노트

08 다중 선형 회귀 구현

가설 함수를 생각하며 선형 회귀를 구현해보자.

✅ 입력변수

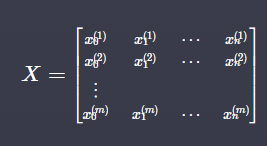
✅ 파라미터 (x 의 계수)

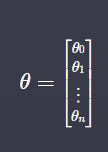
✅ 오차

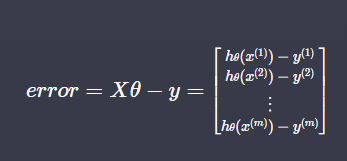
✅ 경사하강법

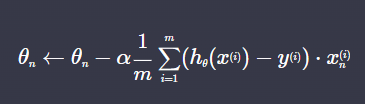
다음과 같은 세타 업데이트는 따라서

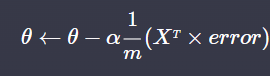
또는

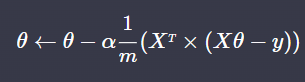
이렇게 표현할 수 있다. 어렵지 않음!

09 가설함수 구현하기

가설함수를 구현하려면 파라미터와 각 x 값을 곱하고 더해주기만 하면 된다. 주의해야 할 것은 모든 자리의 앞에 1값을 추가해줘야 한다는 것이다. 코드를 보자 

import numpy as np

def prediction(X, theta):
    """다중 선형 회귀 가정 함수. 모든 데이터에 대한 예측 값을 numpy 배열로 리턴한다"""
    # 여기에 코드를 작성하세요
    return X @ theta
# 입력 변수수
house_size = np.array([1.0, 1.5, 1.8, 5, 2.0, 2.5, 3.0, 3.5, 4.0, 5.0, 6.0, 7.0, 8.0, 8.5, 9.0, 10.0])  # 집 크기
distance_from_station = np.array([5, 4.6, 4.2, 3.9, 3.9, 3.6, 3.5, 3.4, 2.9, 2.8, 2.7, 2.3, 2.0, 1.8, 1.5, 1.0])  # 지하철역으로부터의 거리 (km)
number_of_rooms = np.array([1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 3, 4, 4, 4, 4])  # 방 수

# 설계 행렬 X 정의
X = np.array([
    np.ones(16),
    house_size,
    distance_from_station,
    number_of_rooms
]).T

# 파라미터 theta 값 정의
theta = np.array([1, 2, 3, 4])

prediction(X, theta)

np.ones() 때문에 X 행렬은 1, 1.0, 5, 1.0 이렇게 각 줄마다 앞에 1 이 들어가게 된다. m = 16이다.

10 다중 선형 회귀 경사 하강법 구현

import numpy as np

def prediction(X, theta):
    """다중 선형 회귀 가정 함수. 모든 데이터에 대한 예측 값을 numpy 배열로 리턴한다"""
    # 지난 실습의 코드를 여기에 붙여 넣으세요
    return X @ theta

def gradient_descent(X, theta, y, iterations, alpha):
    """다중 선형 회귀 경사 하강법을 구현한 함수"""
    m = len(X)  # 입력 변수 개수 저장
    
    for _ in range(iterations):
        # 여기에 코드를 작성하세요
        error = X @ theta - y
        theta = theta-alpha * (1/m) * X.T @ error 
    return theta
    

# 입력 변수
house_size = np.array([1.0, 1.5, 1.8, 5, 2.0, 2.5, 3.0, 3.5, 4.0, 5.0, 6.0, 7.0, 8.0, 8.5, 9.0, 10.0])  # 집 크기
distance_from_station = np.array([5, 4.6, 4.2, 3.9, 3.9, 3.6, 3.5, 3.4, 2.9, 2.8, 2.7, 2.3, 2.0, 1.8, 1.5, 1.0])  # 지하철역으로부터의 거리 (km)
number_of_rooms = np.array([1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 3, 4, 4, 4, 4])  # 방 수

# 목표 변수
house_price = np.array([3, 3.2, 3.6 , 8, 3.4, 4.5, 5, 5.8, 6, 6.5, 9, 9, 10, 12, 13, 15])  # 집 가격

# 설계 행렬 X 정의
X = np.array([
    np.ones(16),
    house_size,
    distance_from_station,
    number_of_rooms
]).T

# 입력 변수 y 정의
y = house_price

# 파라미터 theta 초기화
theta = np.array([0, 0, 0, 0])

# 학습률 0.01로 100번 경사 하강
theta = gradient_descent(X, theta, y, 100, 0.01)

theta

11 정규 방정식

✅ 정규 방정식

정규방정식은 기존의 손실함수에서 경사하강법으로 세타를 찾았던 지난 방법과는 달리 한 번에 미분하여 세타를 찾는 것이다.

손실함수를 미분했을 때 기울기가 0이 되는 지점 (손실이 최소가 되는 지점) 은 다음과 같다.

12 정규 방정식 도출하기

13 다중 선형 회귀 정규 방정식 구현하기

import numpy as np

def normal_equation(X, y):
    """설계 행렬 X와 목표 변수 벡터 y를 받아 정규 방정식으로 최적의 theta를 구하는 함수"""
    # 여기에 코드를 작성하세요
    
    return np.linalg.pinv(X.T @ X) @ X.T @ y
# 입력 변수
house_size = np.array([1.0, 1.5, 1.8, 5, 2.0, 2.5, 3.0, 3.5, 4.0, 5.0, 6.0, 7.0, 8.0, 8.5, 9.0, 10.0])  # 집 크기
distance_from_station = np.array([5, 4.6, 4.2, 3.9, 3.9, 3.6, 3.5, 3.4, 2.9, 2.8, 2.7, 2.3, 2.0, 1.8, 1.5, 1.0])  # 지하철역으로부터의 거리 (km)
number_of_rooms = np.array([1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 3, 4, 4, 4, 4])  # 방 수

# 목표 변수
house_price = np.array([3, 3.2, 3.6 , 8, 3.4, 4.5, 5, 5.8, 6, 6.5, 9, 9, 10, 12, 13, 15])  # 집 가격

# 입력 변수 파라미터 X 정의
X = np.array([
    np.ones(16),
    house_size,
    distance_from_station,
    number_of_rooms
]).T

# 입력 변수 y 정의
y = house_price

# 정규 방적식으로 theta 계산
theta = normal_equation(X, y)
theta

normal_equation 부분을 고치는 것인데,
X를 만들때 .T 는 먼저 4,16 으로 써주고 16.4 의 형태로 X 를 만들기 위해 (쉽게 만들기위해) 써준 것이다.

따라서 방금 봤던 식으로 쓰면 되고, 역행렬은 np.linalg.pinv() 로 계산.

14. 경사하강법 VS 정규 방정식

✅ 경사 하강법

  • 적절한 학습률 알파를 찾아야 한다
  • 반복문 사용
  • n 이 커도 효율적으로 연산 가능

✅ 정규 방정식

  • 학습률 알파 정할 필요 없음
  • 단 한단계로 계산 끝
  • n 이 커질수록 비효율적
  • 계산 과정 중 역행렬이 존재하지 않을 수 있다. (문제는 안됨)

n 이 1000개를 넘느냐 안넘느냐 기준으로 정할 때가 많음. 1000개 넘으면 경사 하강법 쪽으로!

15 Convex 함수

손실함수의 최소 지점을 경사하강법 정규방정식 으로 완벽히 찾을 수 있을까?

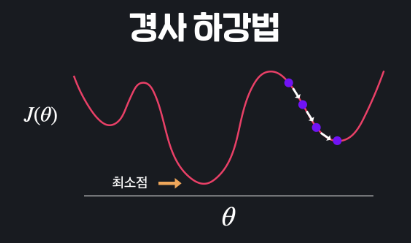
보라색 지점에서 시작한 경사하강법이 찾은 최소지점은 사실은 최저점이 아니다.

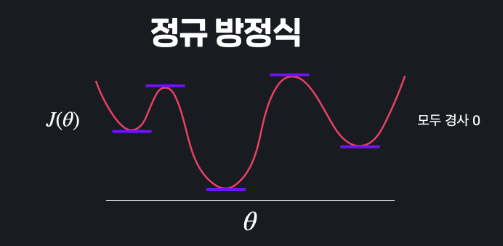
기울기가 0이 되는 지점이 너무 많아 정규 방정식으로도 최저점을 찾지 못한다.

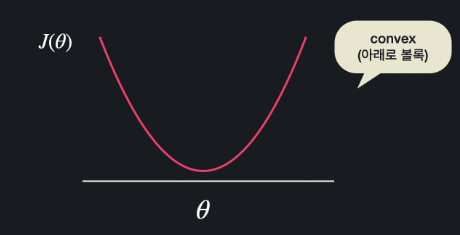
그러나 이렇게 생긴 함수는 경사 하강으로도, 정규 방정식으로도 최소점을 찾는다.

이렇게 아래로 볼록한 함수를 convex 라고 한다.
위의 함수는 non-convex 라 한다.

16 Scikit-learn 데이터 준비

from sklearn.datasets import load_boston
import pandas as pd
boston_dataset = load_boston()
X = pd.DataFrame(boston_dataset.data, columns =  boston_dataset.feature_names)
y = pd.DataFrame(boston_dataset.target, columns =['MEDV'])

✅ feature_names : 속성 확인
✅ .data : 속성 안의 데이터
✅ .target : 결괏값

x 와 y 는 다음과 같은 데이터프레임 상태가 된다. 


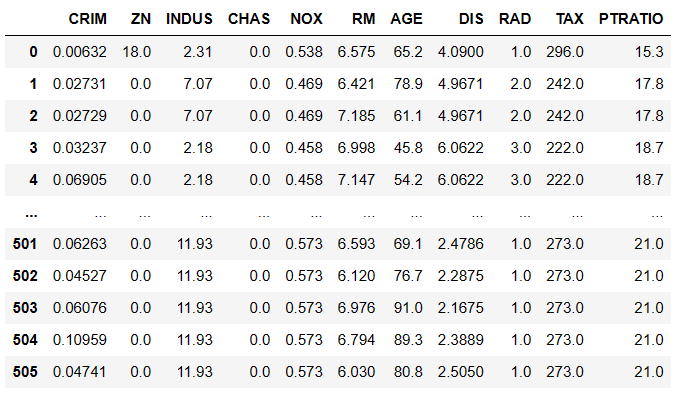
from sklearn.datasets import load_boston
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error

from sklearn.model_selection import train_test_split : 트레이닝용, 테스트용 데이터 나눠준다.
from sklearn.linear_model import LinearRegression : 선형 회귀 모델 확정
from sklearn.metrics import mean_squared_error : 모델 평가시 사용하는 평균 제곱 오차 함수.

17 사이킷런으로 다중 선형 회귀 쉽게 하기

✅ 테스트 데이터로 가설 함수 구하기 

x_train, x_test, y_train, y_test = train_test_split(X, y, test_size = 0.2, random_state = 5)
model = LinearRegression()
model.fit(x_train, y_train)
model.coef_
model.intercept_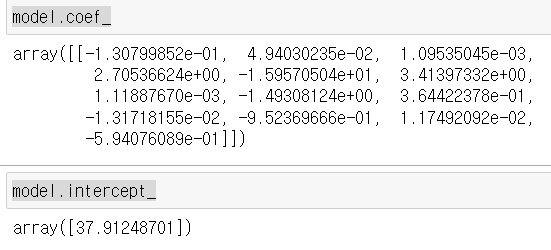

model 은 선형 회귀를 할 수 있게 하는 변수이고, .fit 을 사용함으로서 트레이닝을 통해 모든 세타값들을 확인할 수 있게 한다.

.coef_ : 세타 1부터 n 까지 확인
.intercept_ : 세타0 확인

✅ 테스트 데이터를 통해 실제 예측값 구하기

model.predict() 함수를 사용한다.

✅ 트레인 데이터와 테스트 데이터 오차 구하기

평균제곱오차의 루트를 통해 평균제곱 오차 제곱근을 구한다.

mean_squared_error() 사용

18 scikit-learn 으로 당뇨수치 예측하기

# 필요한 라이브러리 import
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error

import pandas as pd  

# 당뇨병 데이터 갖고 오기
diabetes_dataset = datasets.load_diabetes()

# 입력 변수를 사용하기 편하게 pandas dataframe으로 변환
X = pd.DataFrame(diabetes_dataset.data, columns=diabetes_dataset.feature_names)

# 목표 변수를 사용하기 편하게 pandas dataframe으로 변환
y = pd.DataFrame(diabetes_dataset.target, columns=['diabetes'])

# 여기에 코드를 작성하세요
x_train, x_test, y_train, y_test = train_test_split(X, y, test_size = 0.2, random_state = 5)
model = LinearRegression()
model.fit(x_train, y_train)

y_test_predict = model.predict(x_test)


# 평균 제곱 오차의 루트를 통해서 테스트 데이터에서의 모델 성능 판단
mse = mean_squared_error(y_test, y_test_predict)

mse ** 0.5
profile
박경민
Mathematics, Algorithm, and IDEA for AI research🦖
이전 포스트

선형 회귀 (2)

다음 포스트

다항 회귀

0개의 댓글