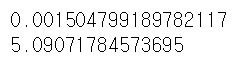정규화 (Regularization)

01 편향과 분산 (Bias, Variance)

편향 : 주어진 데이터를 모델이 얼마나 잘 반영하는지.
예컨대 하나의 점에서 이를 이어 버리는 곡선이 직선보다 편향이 낮을 수 있다.

분산 : 데이터 셋 별로 모델이 얼마나 일관된 성능을 보여주는지.
(하나의 가설함수, 여러 데이터 셋 안에서)
예를들어 곡선이 직선보다 다른 데이터에선 성능이 낮아져서 일관되지 못해, 분산이 클 수 있다.

편향과 분산은 작은 게 좋은 것! (기존 데이터에 잘 맞음, 일관된 성능임)

02 노트

03 편향 - 분산 Tradeoff (Bias - Variance Tradeoff)

직선 : 복잡도가 떨어지므로 곡선 관계를 학습할 수 없다
그러나 어떤 데이터가 주어져도 일관성이 있어 분산이 낮다. (과소적합, underfit)

곡선 : 데이터 자체를 외워 Training 데이터에 대한 성능은 높아 편향은 낮고,
처음보는 test 데이터에서는 성능이 떨어진다. (과적합, overfit)

이를 trade-off 관계 라 한다. 따라서 둘 사이의 적당한 밸런스를 찾아내는 것이 중요하다.

04 노트

05 Scikit-learn 으로 과적합 문제 직접 보기

from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
from sklearn.preprocessing import PolynomialFeatures

from math import sqrt 

import numpy as np
import pandas as pd

admission_df = pd.read_csv('downloads/admission_data.csv').drop('Serial No.', axis = 1)
admission_df.head()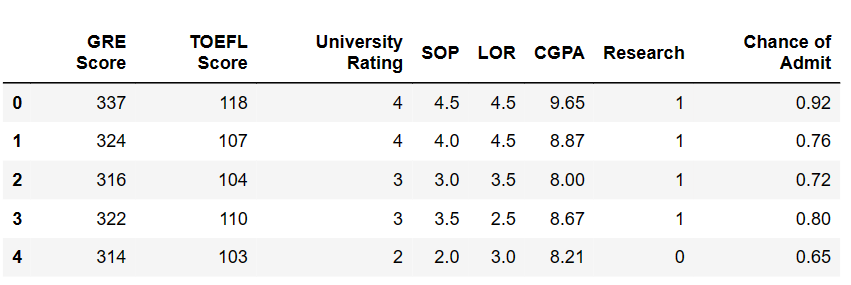

X = admission_df.drop(['Chance of Admit '], axis=1)

polynomial_transformer = PolynomialFeatures(6)
polynomial_features = polynomial_transformer.fit_transform(X.values)
features = polynomial_transformer.get_feature_names(X.columns)

X = pd.DataFrame(polynomial_features, columns = features)
X.head()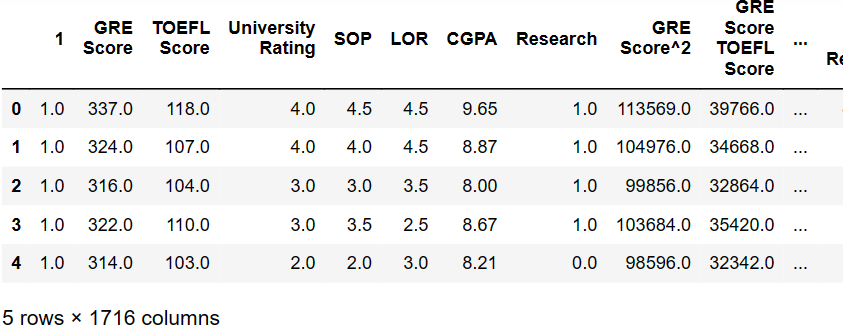

y = admission_df[['Chance of Admit ']]
y.head()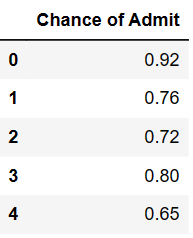

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.3, random_state = 5)
model = LinearRegression()
model.fit(X_train, y_train)
y_train_predict = model.predict(X_train)
y_test_predict = model.predict(X_test)
mse = mean_squared_error(y_train, y_train_predict)
print(sqrt(mse))

mse = mean_squared_error(y_test, y_test_predict)
print(sqrt(mse))