지난 번 학습한 과적합 (overfit) 현상을 방지해주는 정규화에 대해서 알압보자.
06 정규화 개념
정규화 : 세타 값들이 너무 커지는 걸 방지하는 방법.
따라서 과적합을 예방할 수 있다.
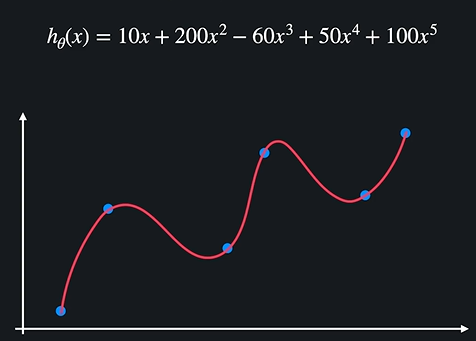
다음 식에서 식이 데이터에 과적합된 까닭은 5차항이어서가 아니라 세타값들이 너무 커져서 과적합 된 것이다. (세타값들이 커지면 각 변수의 영향이 커진다.)
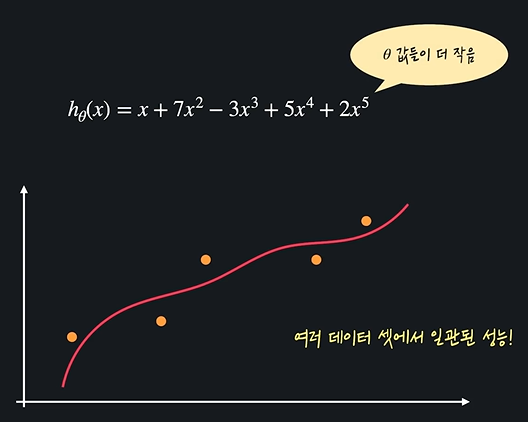
이를 다음과 같이 좀 낮춰줌으로서 해결할 수 있다. 이를 정규화라 한다.
07 노트
08 L1, L2 정규화
정규화 : 손실함수 + 정규화 항
정규화 항이란 무엇일까? : 가설함수를 평가하는 기준을 바꾸는 것이다. 정규화 항의 종류에 따라 L1 (람다 X 절댓값 세타) L2 (람다 X 세타 제곱) 정규화가 있다. 알아보자.
손실함수(J) 는 평균제곱오차 mse 에 1/2 한 것이다. (계산의 편의를 위해)
손실함수는 가설함수를 평가하기 위한 함수라는 것은 기본이다!
오차는 굉장히 작아도 (training 데이터에 맞아도) 세타 값이 너무 클 때 과적합이 일어난다고 했다.
따라서 좋은 가설함수를 평가하는 새로운 기준을 잡을 수 있다. 오차도 작으면서 세타 값도 작아야 한다는 것!
이를 식으로 표현하려면 손실함수를 설정할 때 세타값도 표현한 식을 만들면 된다.
세타값이 커지면 안좋은, 작아지면 좋은 손실함수는 다음과 같이 표현한다.
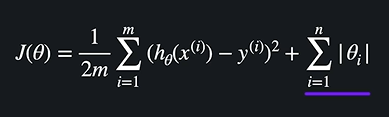
절대값으로 세타를 각각 더하기 때문에 위를 만족시킬 수 있다.
여기서 람다를 곱해준다.
✅ L1정규화
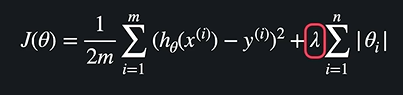
람다는 세타 값들에 대한 페널티이다. 람다가 클수록 세타를 줄이는 게 중요하다는 것, 작을수록 MSE 를 줄이는 게 중요하다는 것이다. L1정규화가 이것이다. L1 정규화를 활용한 것이 Lasso 모델이다.
✅ L2 정규화
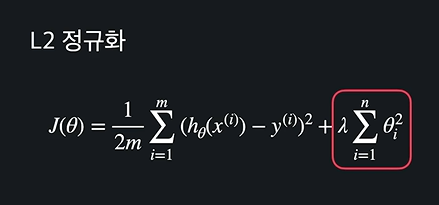
L2는 절댓값 대신 ^2를 한다. L2 정규화를 활용한 것을 Ridge 모델 이라 한다.
09 노트
10 Scikitlearn 으로 과적합 문제 해결
코드는 다음과 같다. 지난 코드에서 import LinearRegression 을 import Lasso 로, model = LinearRegression() 을 model = Lasso() 로 바꿔주는데, 라쏘 모델 안의 파라미터가 좀 있다.
Lasso 파라미터
model = Lasso(alpha = 람다 값, max_iter = 경사하강법 횟수 지정, normalize = True)
normalize = True 는 정규화를 위한 것이고, 나머지는 수를 넣어주면 끝.
from sklearn.linear_model import Lasso
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
from sklearn.preprocessing import PolynomialFeatures
from math import sqrt
import numpy as np
import pandas as pd
admission_df = pd.read_csv('downloads/admission_data.csv').drop('Serial No.', axis = 1)
admission_df.head()
X = admission_df.drop(['Chance of Admit '], axis=1)
polynomial_transformer = PolynomialFeatures(6)
polynomial_features = polynomial_transformer.fit_transform(X.values)
features = polynomial_transformer.get_feature_names(X.columns)
X = pd.DataFrame(polynomial_features, columns = features)
X.head()
y = admission_df[['Chance of Admit ']]
y.head()
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.3, random_state = 5)
model = Lasso(alpha = 0.001, max_iter = 1000, normalize = True)
model.fit(X_train, y_train)
y_train_predict = model.predict(X_train)
y_test_predict = model.predict(X_test)
print('##### train 성능')
mse = mean_squared_error(y_train, y_train_predict)
print(sqrt(mse))
print('##### test 성능')
mse = mean_squared_error(y_test, y_test_predict)
print(sqrt(mse))
지난 번에는 과적합 문제로 train 성능은 과도하게 좋았고, test 는 많이 안좋았다. 그러나 lasso 모델로 적절하게 세타 값이 커지는 걸 방지했더니 trian 성능과 test 성능이 비슷하게 좋아진 것을 확인했다!
11 L1 정규화 직접 해보기
from sklearn.linear_model import Lasso
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
from sklearn.preprocessing import PolynomialFeatures
from math import sqrt
import numpy as np
import pandas as pd
# 데이터 파일 경로 정의
INSURANCE_FILE_PATH = './datasets/insurance.csv'
insurance_df = pd.read_csv(INSURANCE_FILE_PATH) # 데이터를 pandas dataframe으로 갖고 온다 (insurance_df.head()를 사용해서 데이터를 한 번 살펴보세요!)
insurance_df = pd.get_dummies(data=insurance_df, columns=['sex', 'smoker', 'region']) # 필요한 열들에 One-hot Encoding을 해준다
# 입력 변수 데이터를 따로 새로운 dataframe에 저장
X = insurance_df.drop(['charges'], axis=1)
polynomial_transformer = PolynomialFeatures(4) # 4 차항 변형기를 정의
polynomial_features = polynomial_transformer.fit_transform(X.values) # 4차 항 변수로 변환
features = polynomial_transformer.get_feature_names(X.columns) # 새로운 변수 이름들 생성
X = pd.DataFrame(polynomial_features, columns=features) # 다항 입력 변수를 dataframe으로 만들어 준다
y = insurance_df[['charges']] # 목표 변수 정의
# 여기에 코드를 작성하세요
X_train , X_test, y_train , y_test = train_test_split(X, y, test_size = 0.3, random_state = 5)
model = Lasso(alpha = 1, max_iter = 2000, normalize = True)
model.fit(X_train, y_train)
y_train_predict = model.predict(X_train)
y_test_predict = model.predict(X_test)
# 테스트 코드
mse = mean_squared_error(y_train, y_train_predict)
print("training set에서 성능")
print("-----------------------")
print(f'오차: {sqrt(mse)}')
mse = mean_squared_error(y_test, y_test_predict)
print("testing set에서 성능")
print("-----------------------")
print(f'오차: {sqrt(mse)}')12 L2 정규화 직접 해보기
from sklearn.linear_model import Ridge
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
from sklearn.preprocessing import PolynomialFeatures
from math import sqrt
import numpy as np
import pandas as pd
INSURANCE_FILE_PATH = './datasets/insurance.csv'
insurance_df = pd.read_csv(INSURANCE_FILE_PATH)
insurance_df = pd.get_dummies(data=insurance_df, columns=['sex', 'smoker', 'region'])
# 기존 데이터에서 입력 변수 데이터를 따로 저장한다
X = insurance_df.drop(['charges'], axis=1)
polynomial_transformer = PolynomialFeatures(4) # 4 차항 변형기를 정의한다
polynomial_features = polynomial_transformer.fit_transform(X.values) # 데이터 6차 항 변수로 바꿔준다
features = polynomial_transformer.get_feature_names(X.columns) # 변수 이름들도 바꿔준다
# 새롭게 만든 다항 입력 변수를 dataframe으로 만들어 준다
X = pd.DataFrame(polynomial_features, columns=features)
y = insurance_df[['charges']]
# 여기에 코드를 작성하세요
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.3 , random_state = 5)
model = Ridge(alpha = 0.01, max_iter = 2000, normalize = True)
model.fit(X_train, y_train)
y_train_predict = model.predict(X_train)
y_test_predict = model.predict(X_test)
# 테스트 코드
mse = mean_squared_error(y_train, y_train_predict)
print("training set에서 성능")
print("-----------------------")
print(f'오차: {sqrt(mse)}')
mse = mean_squared_error(y_test, y_test_predict)
print("testing set에서 성능")
print("-----------------------")
print(f'오차: {sqrt(mse)}')13 일반화
L1, L2 정규화는 어떤 모델에서든지 중요한 정규화로 다양한 모델에 적용 가능하다. 우리가 살펴본 것은 다중 회귀, 다중 다항 회귀, 로지스틱 회귀 등 다양하게 그 회귀의 가설함수의 뒤에 + 절댓값 세타 / 세타 제곱 의 합을 더해주면 된다.
이때 로지스틱 회귀 에 관해서는 다음과 같이 실행한다.
LogisticRegression(penalty='none') # 정규화 사용 안함
LogisticRegression(penalty='l1') # L1 정규화 사용
LogisticRegression(penalty='l2') # L2 정규화 사용
LogisticRegression() # 위와 똑같음: L2 정규화 사용보통 회귀 이름을 model = Lasso, Ridge 라 하지만 로지스틱은 포함되어 있어 그렇지 않고, 저렇게 파라미터로 표시한다. 만약 적지 않더라도 자동으로 L2 정규화를 사용한다.
14 L1, L2 정규화 차이점
L1 정규화와 L2 정규화는 뒤에 더하는 정규화 항 으로 인해 구하는 세타 값들에 약간의 차이가 생긴다.
L1 정규화는 여러 세타를 0으로 만들어 버린다. 계수가 0이 되므로 필요없는 항들이 삭제가 된다.
L2 정규화는 0까지 아니고 세타를 굉장히 작은 값으로 만들어준다. 왜 이런 차이가 발생할까?
L1 정규화에서 뒤에 더하는 세타를 2차항에서는 세타1, 세타2 두 개가 될 것이다. 따라서 절댓값 세타1, 절댓값 세타2 의 합을 t 라 하면 다음과 같다.
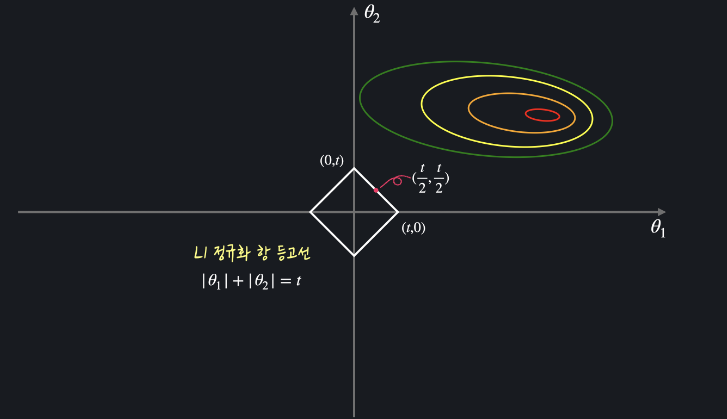
이렇게 마름모꼴인 t가 평균제곱오차 등고선과 만나는 점이 세타들의 최종 좌표인데, 세타 중 하나가 0이 되는 지점에서 자주 만난다.
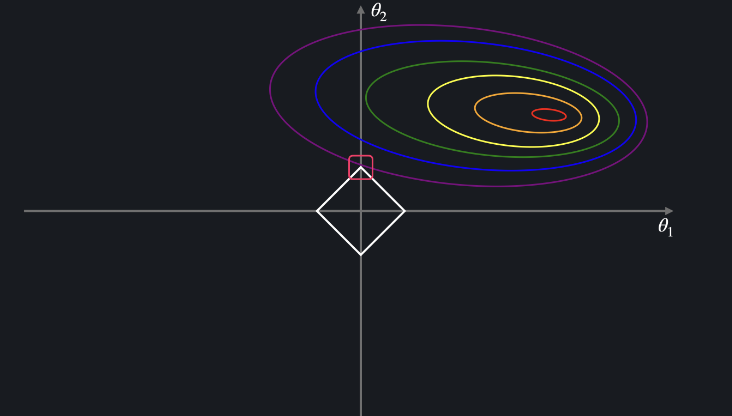
그러나 L2 정규화는 이 t 의 그래프가 원이다. 이유는 제곱의 합이므로 t 자체가 이차식이기 때문이다.

따라서 원으로 세타가 0에서 만나지 않고 좌표 위에서 부드럽게 접한다. 그게 세타의 좌표이다.