[핸즈온 머신러닝] 9. 비지도 학습

비지도 학습은 현재의 대부분 머신러닝 애플리케이션에서는 소외받는 느낌이지만 현실은 다르다. 실제 세계에 존재하는 데이터 중 대부분의 데이터가 라벨이 없는 일반적인 데이터이므로 알고리즘 자체도 레이블이 없는 데이터를 바로 사용할 수 있을 경우 활용 분야가 클 것.

이제 다음과 같은 문제들을 살펴보자.

• 군집
• 이상치 탐지
• 밀도 추정

이를 할 수 있기 위해 k-평균, DBSCAN, 가우시안 혼합 모델과 같은 알고리즘을 사용한다.

9.1 군집

군집이란 비슷한 샘플을 가려내 하나의 클러스터 또는 비슷한 샘플의 그룹으로 할당하는 과정이다.

그렇다면 분류와는 무엇이 다를까? 분류와 군집은 모두 각 샘플이 특정 그룹에 할당되지만, 분류의 그룹은 라벨이 있고 군집의 그룹은 라벨이 없다. (그림에서 왼쪽이 분류, 오른쪽이 군집)

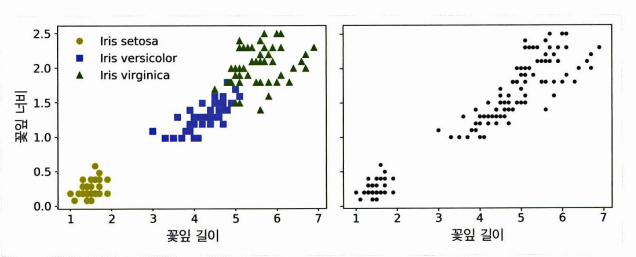
군집은 다음과 같이 적용할 수 있다.🔽
고객 분류 / 데이터 분석 / 차원 축소 기법 / 이상치 탐지 / 준지도 학습 / 검색 엔진 / 이미지 분할

클러스터에 대한 딱 하나의 정의는 없다. 왜냐? 각 알고리즘마다 클러스터를 다르게 정의하기 때문. (클러스터를 찾는 방식이 모두 다르다.) 여러 군집 알고리즘 중 K-평균, DBSCAN, 비선형 차원 축소, 준지도 학습, 이상치 탐지를 알아보자.

9.1.1 k-평균

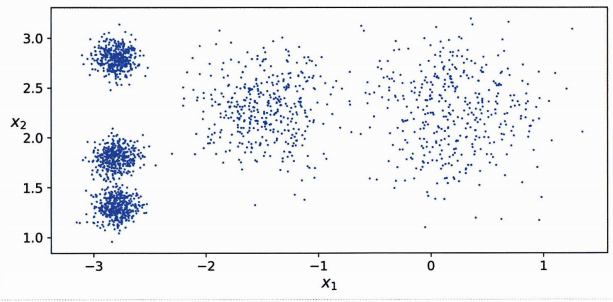
위 데이터는 레이블이 없어도 5개의 덩어리로 클러스터를 묶을 수 있어보인다. 먼저 코드를 보자.

from sklearn.cluster import KMeans 
k = 5
kmeans = KMeans(n_clusters=k, random_state=42)
y_pred = kmeans.fit_predict(X)

k = 5 라는 것은 군집 5개에 각 샘플을 할당하겠다는 것이다. 따라서 X값 인풋을 주면 0-4까지의 군집 중 하나의 군집에 할당된 예측을 반환한다.

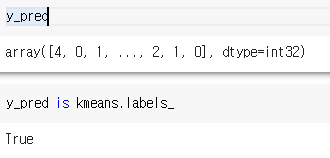
.cluster_centers_ 는 각 군집의 중심인 센트로이드도 확인할 수 있다.

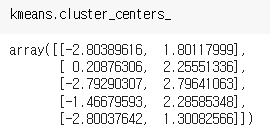
이제 새로운 샘플을 넣으면 해당 샘플의 클러스터를 확인할 수 있다.

X_new = np.array([[0, 2], [3, 2], [-3, 3], [-3, 2.5]])
kmeans.predict(X_new)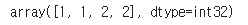

클러스터의 결정 경계는 보로노이 다이어그램이라고 한다. 위 데이터 셋의 결정 경계를 그려보자. (왼쪽 위의 몇 개의 샘플은 가운데 클러스터와 왼쪽 위 클러스터 사이에 잘못 부여되어있다.)

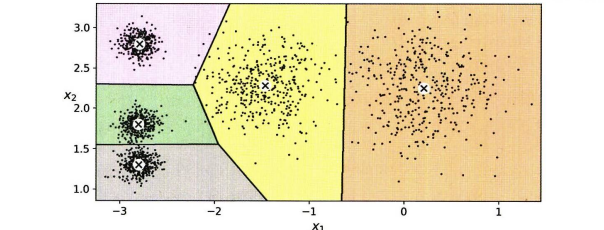
여기서 하드 군집이란 샘플을 하나의 클러스터에 할당하는 것을 말하고, 소프트 군집 이란 클러스터마다 샘플에 점수를 부여하는 것이다. 소프트 군집에서 매기는 점수는 샘플과 군집의 중심 사이의 거리가 된다. 또한 가우시안 방사기저 함수같은 유사도 점수도 점수의 후보이다. .transfomr() 메서드는 샘플과 군집 중심 사이 거리를 반환한다.

kmeans.transform(X_new)

transform 메서드는 결과적으로 각 샘플에 대해 k차원의 데이터셋을 반환하기에 효율적인 비선형 차원 축소 기법이 될 수 있다.

k평균 알고리즘
알고리즘의 작동 과정을 알아보자.

1. 무작위로 k개의 샘플을 뽑아 군집의 중심으로 본다.
2. 각 샘플을 군집에 할당한다
3. 각 클러스터에 속한 샘플의 평균이 새로운 군집의 중심이 된다
4. 군집의 중심에 변화가 없을 때까지 2,3 을 반복.

간혹 군집의 중심이 너무 잘못되었다면 적절한 수렴이 이루어지지 못할 수 있다. 따라서 센트로이드의 초기화 방법이 중요한데, 이 방법을 알아보자.

센트로이드 초기화 방법

• 또다른 군집 알고리즘을 먼저 실행하여 센트로이드 위치를 근사하게 알 수 있다면 init 매개변수에 이 리스트를 담고, n_init = 1 로 설정한다.

good_init = np.array([[-3, 3], [-3, 2], [-3, 1], [-1, 2], [0, 2]])
kmeans = KMeans(n_clusters=5, init=good_init, n_init=1, random_state=42)
kmeans.fit(X)
kmeans.inertia_

inertia_ 는 이너셔라 부르며 각 샘플과 가장 가까운 센트로이드 사이의 제곱 거리의 합이다. 이 이너셔 값이 작을수록 당연히 최적의 솔루션 모델이라고 할 수 있다. score() 메서드는 그냥 이너셔 값에 - 를 붙인 것이다. 점수로 따지면 거리가 작을 수록 높아야 하기 때문.

기본적으로 k-평균 알고리즘 내부에서는 바실비스키가 제안한 k-평균++알고리즘의 초기화 방법 을 사용한다.

k-평균 속도 개선과 미니배치 k-평균
모든 샘플과 중심과의 거리는 계산 시간이 오래 걸려 알고리즘을 속도를 높이기 위해 여러 방법이 제안되었다.

• 찰스 엘칸의 논문에선 삼각부등식을 사용(두 점 사이의 직선은 항상 가장 짧은 거리)

• 스컬리의 논문에선 전체 데이터셋이 아닌 반복마다 미니배치를 사용 (속도는 빠르나 이너셔는 나쁠 여지가 있음)

최적의 클러스터 개수는 어떻게?
단순히 k = 5 가 아니라 올바른 클러스터의 개수는 어떻게 찾을까?

이너셔는 당연하게도 k가 증가함에 따라 작아지므로 무작정 좋은 지표가 아니다.

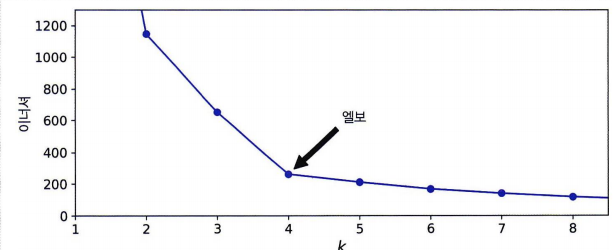
• k와 이너셔에 대한 시각호를 진행했을 때 그래프가 꺾이는 지점을 엘보라고 부르며 이를 클러스터 개수로 지정할 수 있다.
• 또 하나의 방법으로 실루엣 점수가 있으며, 이는 모든 샘플에 대한 실루엣 계수의 평균이다. (b-a)/max(a,b)
• 이때 a는 같은 클러스터에 있는 다른 샘플까지 평균 거리이며, b는 가장 가까운 클러스터까지 평균 거리이다.
• 이 값이 1에 가까우면 자신의 클러스터 안에는 잘 속해 있고 다른 클러스터와 멀리 떨어져 있다는 것
• -1 에 가까우면 잘못된 클러스터에 할당

silhouette_score() 함수를 사용할 수 있다.

from sklearn.metrics import silhouette_score()
silhouette_score(X, kmeans.labels_)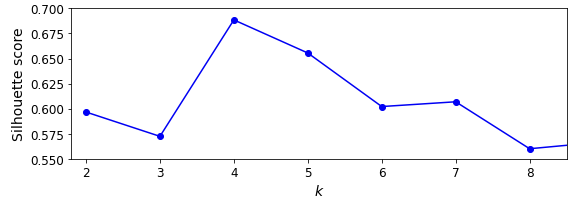

이 점수는 1과 가까울 수록 좋다.

9.1.2 k-평균의 한계

k평균은 장점이 많으나 다음과 같은 한계가 있다.

• 알고리즘을 여러 번 실행해야 한다
• 클러스터 개수를 지정해야 한다
• 크기나 밀집도가 다르거나 원형이 아닐 경우 성능이 떨어진다

9.1.3 군집을 사용한 이미지 분할

• 이미지분할: 이미지를 부분 여러개로 분할하는 과정
• 시맨틱 분할: 동일한 물체의 픽셀은 같은 부분에 할당 > 합성곱 신경망

위 기법 두 가지가 자주 사용하는 이미지 분할의 기본이지만 여기서는 색상 분할을 배워보자. 픽셀이 동일한 색상을 가졌다면 같은 부분으로 할당하는 것!

from matplotlib.image import imread
image = imread(os.path.join('images', 'unsupervised_learning', 'ladybug.png'))
image.shape

impread 로 이미지를 읽을 수 있다.

shape 을 찍어보면 553, 800, 3 이 출력되는데 순서대로 높이, 너비, 컬러 채널 개수이고 컬러가 3인 이유는 RGB이기 때문이다. 따라서 각 픽셀에는 빨, 초, 파랑의 강도가 담긴 3D벡터가 담긴다.

X = image.reshape(-1, 3)
kmeans = KMeans(n_clusters=8, random_state=42).fit(X)
segmented_img = kmeans.cluster_centers_[kmeans.labels_]
segmented_img = segmented_img.reshape(image.shape)

reshape(-1, 3) 을 해줄 때 왜 -1일까? -1은 행의 숫자를 명시적으로 부여하겠다는 것이 아니라 열 숫자에 맞춰 배열하겠다는 것이다. 따라서 R, G, B로 정리된 깔끔한 배열을 얻게되고 k-평균을 써서 색상을 클러스터로 모은다.

• 모든 초록색을 하나의 클러스터로 만든다
• 이 클러스터의 평균 컬러를 찾는다
• 다시 리스트를 이미지로 복구
  

9.1.4 군집을 사용한 전처리

군집은 학습 알고리즘을 적용하기 전 전처리 단계에서도 사용 가능하다.

from sklearn.datasets import load_digits
X_digits, y_digits = load_digits(return_X_y=True)

해당 데이터셋에서는 1797개의 8X8 이미지이며, 각 픽셀은 0-9까지 숫자를 나타내고 있다. 전처리를 하지 않은 상태에서의 훈련 코드만 보자.

from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X_digits, y_digits, random_state=42)

from sklearn.linear_model import LogisticRegression
log_reg = LogisticRegression(multi_class="ovr", solver="lbfgs", max_iter=5000, random_state=42)
log_reg.fit(X_train, y_train)
log_reg_score = log_reg.score(X_test, y_test)
log_reg_score

일반적인 훈련 코드이며, 정확도는 96.9%였다.

이제 k-평균을 전처리 단계로 사용하자. k-평균을 전처리로 사용한다는 것은, 훈련 세트를 k개의 클러스터로 모은 후 이미지를 k개 클러스터까지 거리로 환산한 새로운 데이터셋을 만든다는 것이다.

from sklearn.pipeline import Pipeline
pipeline = Pipeline([
    ("kmeans", KMeans(n_clusters=50, random_state=42)),
    ("log_reg", LogisticRegression(multi_class="ovr", solver="lbfgs", max_iter=5000, random_state=42)),
])
pipeline.fit(X_train, y_train)
pipeline_score = pipeline.score(X_test, y_test)
pipeline_score

출력된 정확도는 97%였다.

물론 여기서도 k개의 적절한 군집 수를 찾기 위해 그리트 탐색을 이용할 수 있다. 그러면 정확도는 더 올라간다.

9.1.5 군집을 사용한 준지도 학습

준지도 학습에서도 군집을 사용할 수 있다. 레이블된 데이터가 레이블이 없는 데이터보다 부족할 때 사용할 수 있다.

n_labeled = 50
log_reg = LogisticRegression(multi_class="ovr", solver="lbfgs", random_state=42)
log_reg.fit(X_train[:n_labeled], y_train[:n_labeled])
log_reg.score(X_test, y_test)

정확도는 83%로 낮게 형성된다. 이럴 경우 훈련 세트를 50개의 클러스터로 모은 후 각 클러스터에서 중심에 가까운 이미지를 찾는다. (대표이미지 찾기)

k = 50
kmeans = KMeans(n_clusters=k, random_state=42)
X_digits_dist = kmeans.fit_transform(X_train)
representative_digit_idx = np.argmin(X_digits_dist, axis=0)
X_representative_digits = X_train[representative_digit_idx]

이런 식으로 대표 이미지 50개를 찾을 수 있다.

y_representative에는 수동으로 정답을 주고 대표이미지를 넣고 훈련한 모델의 성능을 측정해보자.

y_representative_digits = np.array([
    0, 1, 3, 2, 7, 6, 4, 6, 9, 5,
    1, 2, 9, 5, 2, 7, 8, 1, 8, 6,
    3, 1, 5, 4, 5, 4, 0, 3, 2, 6,
    1, 7, 7, 9, 1, 8, 6, 5, 4, 8,
    5, 3, 3, 6, 7, 9, 7, 8, 4, 9])
log_reg = LogisticRegression(multi_class="ovr", solver="lbfgs", max_iter=5000, random_state=42)
log_reg.fit(X_representative_digits, y_representative_digits)
log_reg.score(X_test, y_test)

정확도가 92%로 올라간 것을 확인할 수 있었다. 이런 식으로 라벨 데이터가 부족할 땐 오히려 대표를 찾고 대표에만 정답을 주면 정확도를 높일 수 있다. (해당 군집에 대표의 정답을 다 줘도 좋다.)

9.1.6 DBSCAN

밀집된 연속 지역을 클러스터로 정의한다.

• 엡실론 내에 몇 개의 샘플이 놓여 있는지 센다. (e-이웃)
• e 이웃 내 적어도 min_samples 개 샘플이 있다면 이를 핵심 샘플로 간주
• 핵심 샘플의 이웃에 있는 모든 샘플은 동일한 클러스터로. 이웃에는 다른 핵심 샘플도 포함될 수 있으므로 계속해서 클러스터 확장
• 핵심, 이웃 둘 다 아니라면 이상치

from sklearn.cluster import DBSCAN
from sklearn.datasets import make_moons

X, y = make_moons(n_samples=1000, noise=0.05, random_state=42)
dbscan = DBSCAN(eps=0.05, min_samples=5)
dbscan.fit(X)

9.1.7 다른 군집 알고리즘

병합 군집 / BIRCH / 평균 - 이동 / 유사도 전파 / 스펙트럼 군집 등이 있다.

9.2 가우시안 혼합

다음 글에서 알아보자!