이번 글에선 가우시안 혼합 에 대해서만 정리할 예정이다.
가우시안 혼합 모델은 밀집도 추정, 군집, 이상치 탐지에 사용할 수 있다.
가우시안 혼합
가우시안 혼합 모델은 샘플이 파라미터가 알려지지 않은 여러 개의 혼합된 가우시안 분포에서 생성되었다고 가정하는 확률 모델이다. 따라서 하나의 가우시안 분포에서 나온 모든 샘플은 하나의 클러스터를 형성한다.
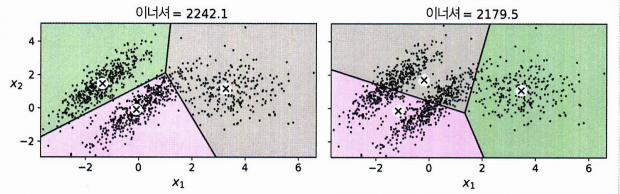
- 클러스터는 대부분 타원 모양이나 클러스터의 크기, 밀집도, 방향, 모양은 다 다르다
- 가우시안 분포에서 샘플이 나온다
- 분포의 파라미터를 알지는 못한다.
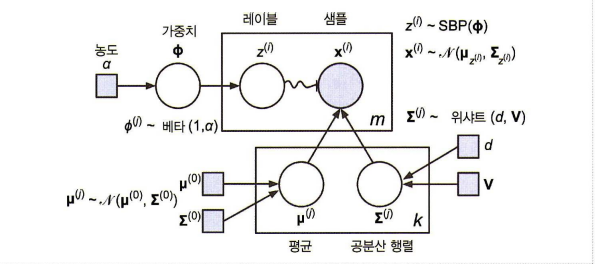
GaussianMixture 클래스는 GMM 의 변종으로 가우시안 분포의 개수 k를 알아야 한다. 데이터셋은 다음과 같이 생성된다.
- 샘플마다 k개의 클러스터에서 한 클러스터가 선택된다.
- 이때 j번째 클러스터를 선택할 확률은 클러스터의 가중치 파이(j)이다.
- i번째 샘플의 클러스터 인덱스는 z(i) 이다.
- i 번째 샘플이 j번째 클러스터에 할당되었다면 z(i) = j 이며, 해당 샘플은 가우시안 분포에서 랜덤하게 샘플링된다.
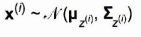
- 클러스터의 평균, 클러스터의 공분산 분포를 따르는 위치 x
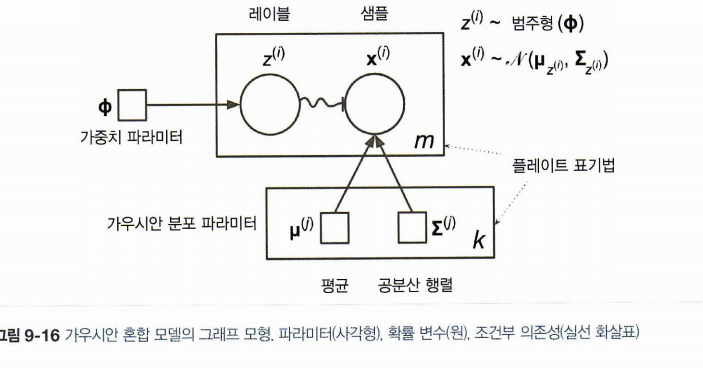
데이터셋 X가 주어지면 가중치 파이, 전체분포의 파라미터(평균과 공분산)를 추정한다. 코드를 보자.
from sklearn.mixture import GaussianMixture
gm = GaussianMixture(n_components=3, n_init=10, random_state=42)
gm.fit(X)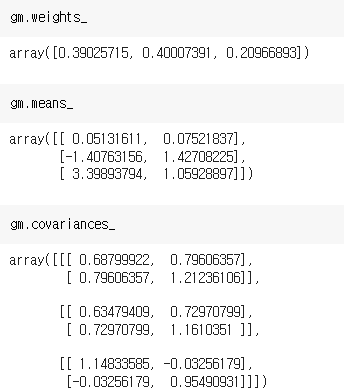
가우시안 혼합 모델을 훈련하고 추정한 파라미터를 확인하는 과정이다. 실제 데이터의 가중치도 0.2, 0.4, 0.4 이므로 잘 추정했다. 이외에도 평균과 분산을 찾는데 기댓값-최대화(EM) 알고리즘을 사용한다. 샘플을 클러스터에 할당하는 것이 기댓값 단계, 클러스터를 업데이트(이 경우 평균, 분산, 클러스터 가중치를 찾아나간다)하는 최대화 단계를 말한다.
훈련시킨 가우시안 혼합 모델은 새로운 샘플을 클러스터에 할당하거나, 새로운 샘플을 만들거나(생성모델의 역할!), 밀도를 추정할 수 있다.
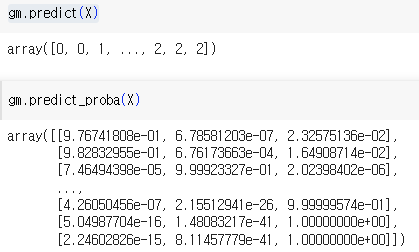
이와 같이 .predict() 나 .predict_proba() 를 사용해 샘플을 클러스터에 할당 또는 클러스터에 속할 확률을 예측하고

.sample() 를 통해 샘플을 생성하고 또다시 예측에 사용할 수 있다.

score_samples() 를 이용하면 밀도를 추정할 수 있다.
1. 가우시안 혼합을 사용한 이상치 탐지
가우시안 혼합을 이용해 이상치를 탐지하는 간단한 방법은 앞서 보았던 score_samples() 메서드를 이용해 밀도를 추정하고, 밀도가 낮은 지역은 이상치로 간주하는 것이다. (이 경우 tradeoff 를 감안한 밀도 임곗값을 정하는 것이 필요.)
densities = gm.score_samples(X)
density_threshold = np.percentile(densities, 4)
anomalies = X[densities < density_threshold]- 이상치는 densities < densitiy_threshold 인 X이다
- density_threshold에는 매개변수로 밀도와 백분위수(여기서는 4%)를 임곗값으로 준다.
2. 클러스터 개수 선택하기
가우시안 혼합 모델 역시 특정 가우시안 분포에서 샘플이 나온다고 가정했을 때, 이 클러스터의 개수를 선택해야 하나 기존 실루엣 점수와 같은 지표를 사용할 수 없다. (클러스터 타원, 크기에 따라 불안정)
대신 이론적 정보 기준을 최소화하는 모델을 찾는다. BIC(Bayesian information criterion), AIC(Akaike information criterion) 과 같은 기준을 찾는다.
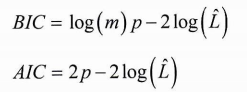
- m: 샘플의 개수
- p: 모델이 학습할 파라미터 개수
- L_hat: 모델의 기능도 함수(likelihood function) 의 최대값
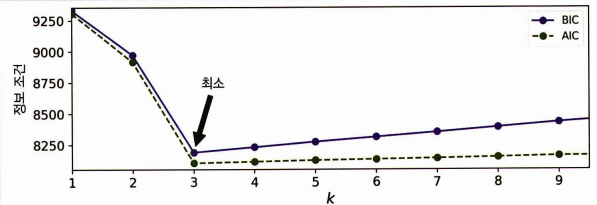
BIC, AIC 의 값은 최소화의 대상이며 이 값이 최소화되는 모델을 찾는다. 학습할 파라미터가 많은 모델(p의 값이 높은 모델)에게 페널티를 가하고, 데이터에 잘 학습하는 모델에게(L이 높은 모델) 보상을 더한다. 따라서 클러스터 개수에 있어 적절한 모델이란 파라미터가 적고, 데이터에 잘 맞는 모델만을 선택하는 것이다. (어찌보면 당연하다!)
클러스터 개수 k가 커질수록 결국은 모델의 수가 증가한다는 것이며 자연히 불필요한 모델도 증가할 것이다.(여기서는 파라미터만 많고 기능은 떨어지는) 그림으로 보듯이 BIC, AIC 가 최소가 되는 k 값을 선택하면 된다!
3. 베이즈 가우시안 혼합 모델
기존 GauusianMixture 을 사용할 때 각 클러스터에 할당된 가중치에 대해 불필요한 가중치를 아예 0 으로 만드는 것이 BayesainGaussianMixture 클래스이다.
가중치를 0으로 만든다는 건 결국 필요한 모델만 한정해 사용하겠다는 것 = 필요한 클러스터 개수를 자동으로 찾는 과정이 가능해진다.
from sklearn.mixture import BayesianGaussianMixture
bgm = BayesianGaussianMixture(n_components=10, n_init=10, random_state=42)
bgm.fit(X)
np.round(bgm.weights_, 2)
다른 값은 모두 0으로 수렴했으므로 3개 정도의 클러스터면 충분하다는 것을 감지했다.
베이지안 + 가우시안 혼합 모델에선 이처럼 클러스터 파라미터(가중치 / 평균/ 공분산)이 고정이 아닌 잠재 확률 변수이다. (z가 클러스터 파라미터, 클러스터 할당을 포함한다.)
4. 이상치 탐지와 특이치 탐지를 위한 알고리즘
PCA, Fast-MCD, 아이솔레이션 포레스트 , LOF, one-class SVM 등이 있다.