Effective active learning in digital pathology: A case study in tumor infiltrating lymphocytes
논문 정리

본 포스팅은 제가 읽었던 논문을 간단하게 정리하는 글입니다. 논문의 모든 내용을 작성하는 것이 아닌, 일부분만 담겨 있으므로 자세한 내용은 원본 논문을 확인해 주시기를 바랍니다. 또한, 논문을 잘못 이해한 부분이 있을 수 있으므로, 양해 바랍니다.
Overview
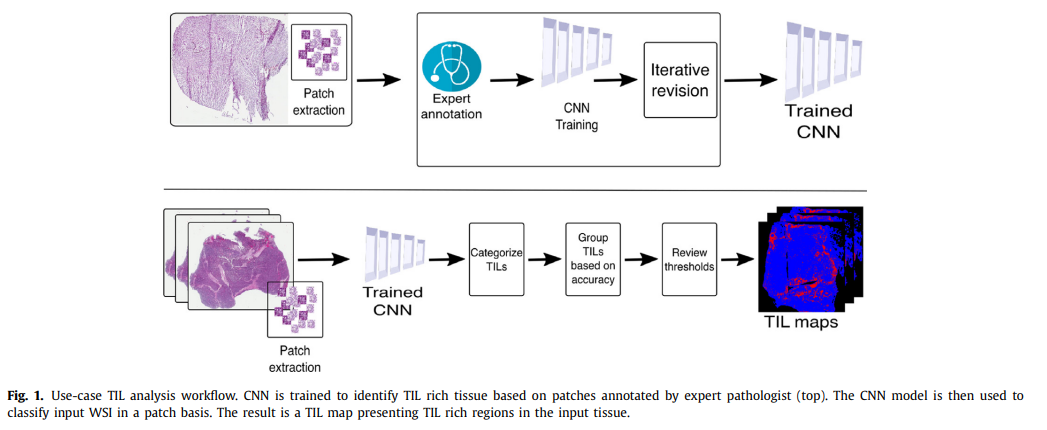
하나의 WSI에는 만 개 단위의 patch가 생성될 수 있음. 모든 patch에 대해 레이블링 작업을 수행하는 것은 매우 어려운 일임. 또한, 작업의 난이도 상 크라우드소싱을 사용한 레이블링 작업 또한 어려움이 있음.
레이블 획득 작업이 어려움에 따라 모델 학습에 사용할 수 있는 그럴듯한 합성 이미지 생성 연구 또한 진행되고 있으나, 이미지 생성 과정 또한 어려움이 있음.
본 논문에서는 레이블 획득이 어려운 문제 상황에 적용하기 위한 active learning 알고리즘인 Diversity-Aware Data Acquisition(DADA) 알고리즘을 제안함. 해당 알고리즘은 active learning의 query 과정에서, 데이터 샘플의 uncertainty와 diversity를 모두 고려함.
Active Learning
Active Learning에도 다양한 종류가 있겠지만, 본 논문에서는 pool-based active learning 방법을 소개함.
Pool-based active learning에서는 전체 unlabeled data points 과 초기의 labeled data points 을 사용함. 번째 각 AL 반복마다 모델은 개의 unlabeled data points를 oracle에게 query 함.
이때 oracle은 patch 단위의 레이블링 작업을 수행할 수 있는 expert이며, query된 data point의 label을 판단하여 모델에게 전달함.
에서 개의 샘플을 선택하는 것이 active learning의 중요한 부분임.
Query Sample Acquisition
모델이 맞추기 쉬운 데이터를 query 하는 것은 의미가 없음. 모델이 헷갈려 하는, 다른 말로 하면 uncertainty가 높은 샘플을 oracle에게 전달해야 함.
CNN에서 uncertainty를 계산하는 방법은 Monte-Carlo Dropout (or Bayesian)과 Ensembles of CNN이 있음. MC Dropout의 경우 test phase에서도 dropout 기능을 활성화하여 동일한 테스트 샘플이라도 다른 결과를 얻도록 하는 것을 의미하며, 이를 통해 예측에 대한 분산 및 disagreements를 계산할 수 있음(번의 반복 입력이 필요함).
앙상블의 경우, 동일 데이터에서 다른 가중치 초기화를 사용한 개의 모델을 사용함. 한 샘플에 대해 개의 예측 결과를 얻을 수 있으므로, 예측에 대한 분산 및 disagreements를 계산하여 이 값을 uncertainty로 사용할 수 있음.
다른 방법으로는 geometric apporach가 있음. CoreSet으로 소개된 이 방법은, 전체 데이터셋을 가장 잘 표현할 수 있는 샘플을 찾아 oracle에게 query 하는 전략임. 해당 알고리즘의 도식을 그림으로 표현하면 아래와 같음.
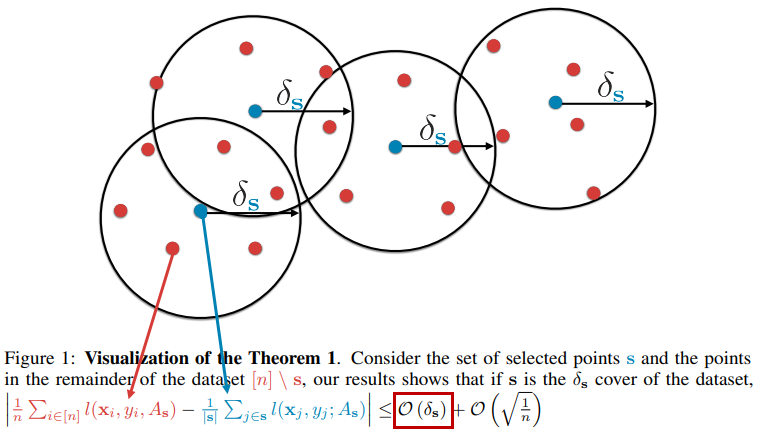
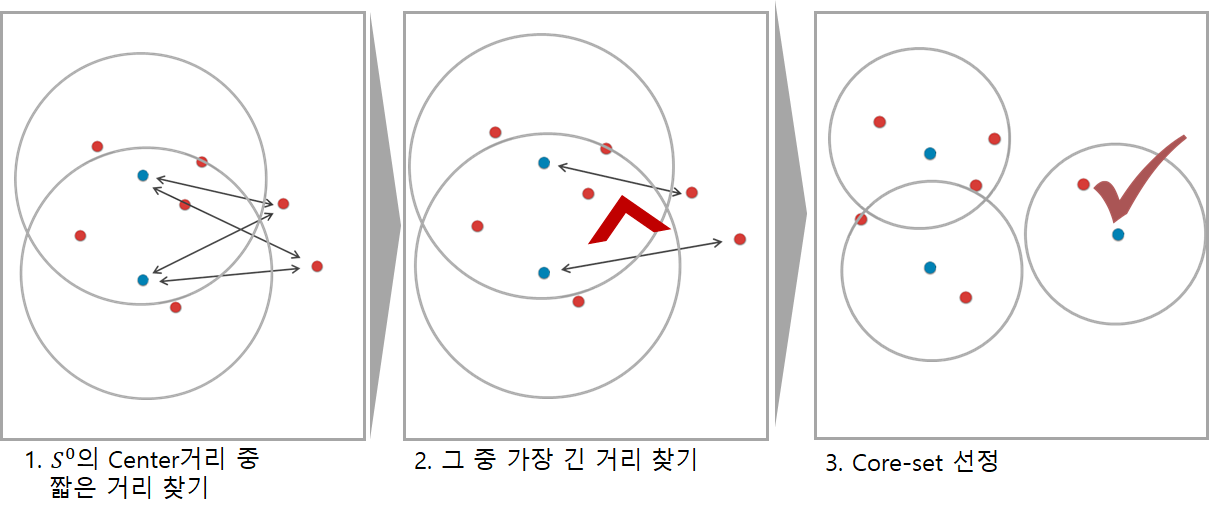
[이미지 출처 : https://kmhana.tistory.com/6]
CoreSet의 경우 Uncertainty보다 Diversity에 집중하는 경향이 있음. 즉, 모델이 헷갈리는 데이터를 찾기보다 데이터의 분포를 커버할 수 있는 다양한 데이터를 찾고자 함.
Uncertainty 기반의 샘플 선택은 선택되는 샘플이 유사해질 수 있음. 직관적으로 생각했을 때, uncertainty 기반의 방법은 모델이 헷갈려 하는 샘플을 query 하는 것이므로, 비슷한 샘플을 계속 query 할 것임.
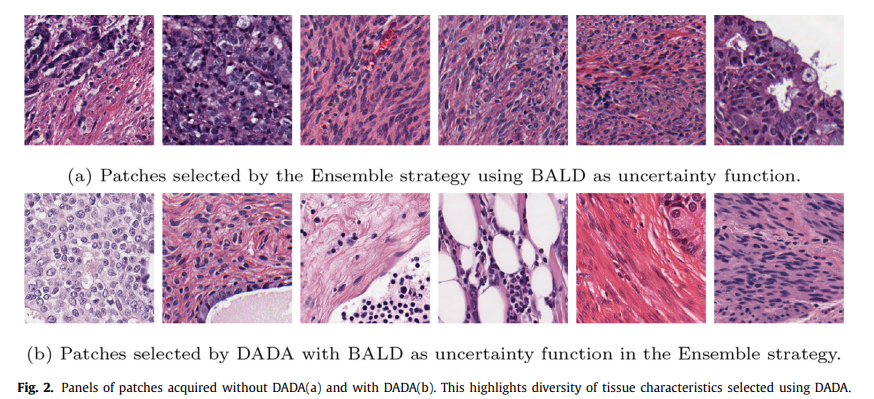
위의 이미지를 보면, uncertainty 기반의 방법은 유사한 patch를 선택함. 본 논문에서 제안하는 DADA 알고리즘(아래 이미지)은 diversity를 고려하여 보다 다양한 patch가 선택된 것을 확인할 수 있음.
Diversity-Aware Data Acquisition (DADA)
Algorithm
DADA 알고리즘은 다음의 과정을 따름.

Line 1
Unlabeled data를 훈련된 CNN(backbone)에 입력하면, 해당 데이터에 대한 deep features(DF)를 얻을 수 있음. 앞서 언급한 MC Dropout / Ensemble 기반의 uncertainty 계산을 통해 해당 데이터에 대한 uncertainty(PU) 또한 계산할 수 있음.
동일 입력에 대한 분산 정도(VR) 혹은 출력의 불일치(disagreements, BALD)를 uncertainty로 사용할 수 있음
Line 2, 3, 4
이후 계산된 DF에 PCA를 적용하여 차원 축소함. 차원 축소된 데이터(DFR)에, 개의 클러스터를 가지는 KMeans 알고리즘을 적용함. 클러스터 내 각 데이터의 uncertainty를 기반으로 클러스터 내 데이터 순서를 정렬함.
Line 5, 6, 7
각 번째 클러스터마다 개의 샘플을 선택함. 는 각 클러스터마다 달라지며, 평균 uncertainty가 높은 클러스터가 많은 샘플을 선택할 수 있도록 처리함(PR()). 각 클러스터는 데이터의 uncertainty로 정렬되었으므로, 상위 개의 샘플을 선택하여 최종 query 집합 A를 얻음.
AL with subpooling
훈련에 사용하는 모든 patch에 대해 차원 축소, 클러스터링, 정렬 작업 등을 수행하는 것은 많은 시간이 필요할 수 있음. 이 부분을 보완하기 위하여 전체 unlabeled data points 에서 일부를 선택(subpooling)하여 DADA 알고리즘을 적용함.
Result
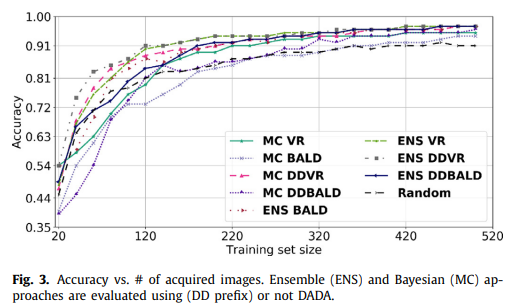
MNIST 데이터와 tumor infiltrating lymphocyte (TIL) regions in whole slide tissue images 데이터를 사용하여 실험하였음.
다른 알고리즘에 비해 기준 AUC 달성을 위해 더 적은 샘플을 사용하였으며, Active Learning execution time 또한 향상되었음. 보다 자세한 실험 결과는 논문을 참고.
