---

본 포스팅은 제가 읽었던 논문을 간단하게 정리하는 글입니다. 논문의 모든 내용을 작성하는 것이 아닌, 일부분만 담겨 있으므로 자세한 내용은 원본 논문을 확인해 주시기를 바랍니다. 또한, 논문을 잘못 이해한 부분이 있을 수 있으므로, 양해 바랍니다.

ABSTRACT

시계열 데이터의 예측 방법에 대한 연구가 많은 관심을 받고 있음. 다양한 분야에서 점점 더 많은 시계열 데이터가 생산되고 있으며, 이러한 시계열 데이터들은 시계열 연구의 발전을 촉진함.

매우 복잡하고 대규모의 시계열 데이터가 생성됨에 따라 시계열 데이터에 대한 예측 모델을 구축하는 것이 더 어려워지고 있음. 시계열 데이터 모델링의 주요 과제는 시계열 데이터의 높은 복잡성, 예측 모델의 낮은 정확도 및 낮은 일반화 능력임.

본 논문에서는 시계열 데이터에 대한 기존의 모델링 방법들을 살펴보고 이를 분류하고자 함. 또한 다양한 방법들을 비교하고 시계열 예측이 나아가야 할 방향을 제시함.

1. INTRODUCTION

시계열 데이터는 특정 프로세스를 일정한 간격의 시간 동안 주어진 샘플링 속도로 관찰한 결과를 말함. 시계열 데이터는 농업, 산업, 금융, 기상 등 다양한 분야에서 빠른 속도로 생성되고 있음.

시계열 분석의 핵심은 데이터에서 법칙을 발견하고 과거의 관찰 결과를 바탕으로 미래 가치를 예측하는 것임. 전통적인 시계열 예측 방법은 확률과 통계에 기반하였으며, 기상, 금융, 산업 등의 분야에서 큰 성과를 이루었음.

그러나 빅데이터 시대가 도래함에 따라 다양한 분포에 속하는 방대한 비선형 시계열 데이터가 지속적으로 생성되고 있으며, 시계열 예측에 큰 어려움이 되고 있음.

따라서 사람들은 매우 복잡한 시계열 데이터 예측 방법에 머신러닝과 딥러닝을 적용하였고, 큰 성과를 거둠. 본 논문에서는 기존의 다양한 시계열 예측 방법을 분류하고자 함.

2. PREDICTION ISSUE OF TIME SERIES

시계열 예측 방법 연구에는 큰 발전이 있었지만, 여전히 몇 가지의 문제가 존재함. 이번 섹션에서는 데이터 측면과 모델 측면에서 몇 가지 문제를 소개함.

2.1 IN TERM OF DATA

데이터의 품질은 데이터 분석과 모델링에서 큰 영향을 주며 결정적인 역할을 함. 그러나, 현실 세계의 데이터는 완벽하지 않음.

시계열 데이터는 센서, 스마트 단말 장치, 수집 시스템 및 기타 실험 기기에서 생성됨. 데이터 수집 장비의 안정성 등 다양한 요인으로 인해 데이터에는 노이즈, 결측치 등 비정상적인 요소가 포함되어 있음.

샘플 데이터의 분포 패턴에 따라 이상값과 결측값을 처리하는 방법은 대규모 시계열 데이터 전처리 방법에서의 중요한 과제임.

2.2 IN TERM OF MODEL

과거 데이터를 기반으로 예측 모델을 구성하고 미래 데이터를 예측하는 것이 일반적인 방법임. 그러나, 실제 현장에서 시간이 지남에 따라 예측 모델의 정확도와 성능이 점차 저하되는 것을 확인함.

이러한 성능 저하의 원인은 과거 데이터와 실시간 데이터 간의 격차 때문임. 또한 새로운 데이터는 모델에 의해 점진적으로(incrementally) 학습되지 않고 예측에 사용됨.

Online incremental data를 기반으로 한 시계열 예측의 수정 모델에 대한 연구는 중요한 문제가 되었음.

2.3 IN TERM OF REAL_TIME CALCULATION

다양한 분야의 시계열 데이터의 급속한 증가와 데이터의 적시성에 대한 요구(demand for timeliness of data)로 실시간 온라인 시계열 분석이 개발 요구 사항이 되었음.

이제 시계열 분석 모델은 일반적으로 독립형 모드(stand-alone mode)를 채택하며, 고성능 GPU 서버를 사용하여 운영 효율을 향상시킴.

한편으로는 GPU 서버는 고가이므로 더 많은 연구 비용이 필요하게 됨. 컴퓨팅 리소스와 데이터 규모의 영향으로 실시간 컴퓨팅을 실현할 수 없다는 문제점 또한 존재함.

3. TAXONOMY OF THE PREDICTION APPROACHES FOR TIME SERIES

시계열 예측 방법의 발전 과정에 따라 기존에 널리 사용되는 시계열 예측 방법을 1) 고전적 시계열 예측 방법, 2) 머신러닝 및 딥러닝 예측 방법, 3) 하이브리드 시계열 예측 방법의 세 가지로 분류함.

3.1 EQUATIONS CLASSICAL FORECASTING METHOD OF TIME SERIES

시계열의 고전적인 예측 방법은 수학적, 통계적 모델링을 기반으로 함. 고전적인 선형 모델에는 주로 autoregressive (AR) 모델, moving average (MA) 모델, autoregressive moving average (ARMA) 모델 autoregressive integrated moving average (ARIMA) 모델이 포함됨.

고전적인 비선형 모델에는 주로 Threshold Autoregressive (TAR) 모델, Constant Conditional Correlation (CCC) 모델, conditional heteroscedasticity 모델이 포함됨.

추가로, 다음과 같은 exponential smoothing에 기반한 몇 가지 중요한 고전적 예측 방법이 존재함: Simple Exponential Smoothing (SES), Holt’s linear trend method, Holt-Winters’ multiplicative method, Holt-Winters’ additive method and Holt-Winters’ damped method.

3.1.1 THE CLASSIC LINEAR MODELS

PREDICTION MODEL FOR STATIONARY DATA

Stationary 시계열 데이터 예측을 위해 Yule은 시계열에 randomness 개념을 도입하고 각 시계열을 random process의 구현으로 간주하여 Auto regressive(AR) 모델을 제안하였음.

이후 연구자에 의해 Moving Averaging (MA) 모델이 제안되었고 Wold는 유명한 Wold decomposition theorem을 제안하였음. Wold decomposition theorem는 시계열 예측 연구의 토대를 마련하였음.

AR, MA, ARMA 모델이 제안되었으며 이 모델들은 stationary 시계열 모델링에 널리 사용됨.

ARMA 모델은 stationary 시계열을 예측하는 데 가장 일반적인 모델임. 이 모델은 시계열 데이터를 랜덤 시퀀스로 간주하며, 이러한 랜덤 변수의 종속성은 시간에 따른 원본 데이터의 연속성을 반영함.

예를 들어, 입력 변수 $x_1, x_2, \cdots, x_p$ 가 주어졌을 때 다음의 회귀식을 얻을 수 있음.

$Y_t = \beta_1x_1 + \beta_2x_2 + \cdots + \beta_px_p + Z$

여기서 $Y$는 예측 대상의 관측값이고 $Z$는 오차임.

예측의 대상인 $Y_t$는 자체 변화의 영향을 받으며, 영향을 받는 법칙은 다음과 같은 공식으로 표현할 수 있음.

$Y_t = β_1Y_{t−1} + β_2Y_{t−2} + \cdots + β_pY_{t−p} + Z_t$

오차(에러) $Z_t$는 기간에 따라 종속 관계가 있으며 그 관계는 다음의 공식으로 표현할 수 있음.

$Z_t = ε_t + α_1ε_{t−1} + α_2ε_{t−2} + \cdots + α_qε_{t−q}$

그러므로, ARMA 모델은 다음의 수식으로 표현됨.

$Y_t = β_0 + β_1Y_{t−1} + β_2Y_{t−2} + \cdots + β_pY_{t−p} + ε_t + α_1ε_{t−1} + α_2ε_{t−2} + \cdots + α_qε_{t−q}$

시계열 $y_t$가 위의 공식을 만족하는 경우, 시계열 $y_t$는 ARMA(p, q)를 따름.

현재 ARMA 모델은 다양한 분야의 시계열 예측에 널리 사용되고 있으며 훌륭한 결과를 얻었음. 다음과 같은 적용 결과가 있음.

• Standard & Poor’s 500 Index와 the London Stock Exchange의 시계열 주식 수익률에 대한 월별 및 연간 예측
• 발전 시스템의 단기 전력 부하 예측
• 대기오염 변수 기반 결핵 발생률 예측

순서를 알 수 없는 ARMA 모델의 예측 구간 구축을 목표로 부트스트랩 분포(p, q)를 기반으로 한 예측 구간 부트스트랩 알고리즘이 제안되었으며, 이는 사전 추정된 순서 값을 사용한 방법에 비해 예측 구간의 coverage 정확도를 크게 향상 시켰음.

Inoue는 다변량 ARMA 프로세스의 유한 예측 계수에 대한 close-form expression을 도출하고 이 식을 적용하여 autoregressive 모델 피팅 및 부트스트랩에 나타나는 합의 점근적 거동(asymptotic behavior of a sum that appears in the autoregressive model fitting and the autoregressive sieve bootstrap)을 결정하였음.

범주형(nominal or ordinal) 시계열을 모델링하기 위한 ARMA의 이산형 확장 모델이 WEISS C H.에 의해 제안되었음. 이 모델은 관측 기반 regimeswitching 메커니즘을 사용하며 RS-DARMA 모델군으로 이어짐.

RS-DAR(1) 모델은 해석하기 쉬운 데이터 생성 메커니즘을 가지고 있으며 negative forms of serial dependence 또한 처리할 수 있음.

Granger causality가 제안됨에 따라 일변량 시계열 모델이 다변량 시계열 분석으로 확장되었음. ARMA 모델을 기반으로 한 multivariate promotion 모델 Vector Autoregressive Moving Average (VARMA)이 제안되었고, 이 모델은 Vector Autoregressive (VAR) 과 Vector Moving Average (VMA) 모델을 유연하게 표현할 수 있음.

VARMA 모델을 구성할 때는 시계열 데이터가 stationary 해야 함. 만약 데이터가 non-stationary 하다면 1차 차분을 통해 stationary 데이터를 얻어야 함.

데이터 존재하는 추세(trend) 정보는 차분 처리에서 무시됨. 이러한 문제를 해결하기 위해 시계열 간의 공적분 관계를 잘 고려할 수 있는 Vector Error Correction Model (VECM)이 제안되었음.

요약하면, ARMA 모델은 stationary 시계열 예측에서 큰 성과를 거두었음. 그러나 실시간 시계열 데이터에는 순수하게 stationary 데이터가 거의 존재하지 않음. 따라서 ARMA 모델의 적용은 데이터의 특성에 따라 제한되며 범용성이 떨어짐.

PREDICTION MODEL FOR NONSTATIONARY DATA

추세, 계절성, 주기성과 같은 특성을 포함하는 시퀀스를 non-stationary 시퀀스라 함. non-stationary 시계열은 local level이나 추세를 제거한 후 homogeneity를 나타낸다는 의미임.

Non-stationary 시계열은 차분 처리 후 stationary 시계열로 변환할 수 있음. ARIMA(p, d, q)는 잘 알려진 non-stationary 시계열 모형으로, 다양한 데이터 패턴의 변화를 반영할 수 있으며 적은 매개변수를 필요로 함.

ARIMA 모델은 다음 식으로 설명됨. $∇$을 차분 연산자로 표시하면, 다음의 결과를 얻음.

$∇^2y_t = ∇(y_t − y_{t−1}) = y_t − 2y_{t−1} + y_{t−2}$

$B$를 delay 연산자로 하면 다음과 같음.

$y_{t−p} = B^py_t, \quad (∀p ≥ 1)$
$∇^k = (1-B)^k$

$y_t$가 차수 $d$의 second non-stationary 시계열이면 $∇^dy_t$는 stationary 시계열이며 다음과 같이 ARMA(p, q) 모델로 설정할 수 있음.

$\lambda(B)(\nabla^dy_t)=\theta(B)ε_t$

이때 $λ(B) = 1− λ_1B −λ_2B^2 − \cdots - λ_pB^p$인 autoregressive coefficient polynomial이며, $θ(B) = 1 − θ_1B − θ_2B^2 − \cdots − θ_pB^p$인 moving average coefficient polynomial임. $ε_t$는 zero-mean인 white noise sequence임.

위의 조건이 만족되면, 이 모델을 autoregressive integrated moving average (ARIMA(p, d, q)) 모델이라고 부름. $d=0$이면 ARIMA 모델은 ARMA 모델과 동일함. 따라서, $d$ 값이 0인지 여부에 따라 해당 시퀀스가 stationary 인지 아닌지 판단할 수 있음.

ARIMA 모델을 구성하기 전에 order(p, q)를 결정해야 함. Autocorrelation Function(ACF)과 Partial Autocorrelation Function (PACF)이 order 결정에 주로 사용됨. 또한, Akaike Information Criterion (AIC)과 Bayesian Information Criterion (BIC)도 레퍼런스용으로 사용됨.

Information criterion은 예측 잔차를 고려할 뿐만 아니라 과적합에 대한 페널티를 추가함. 모델의 order를 결정한 후, Least Squares Estimation (LSE), Maximum Likelihood Estimation (MLE), Bayesian estimation과 같은 방법으로 ARIMA 모델의 파라미터를 추정함.

현재 ARIMA 모델은 비교적 간단한 시계열 예측에 좋은 성과를 거두었음. 다음과 같은 예시가 있음.

• 50년간의 강우량 데이터를 기반으로 이란 주요 지역의 강우량 예측
• PM2.5 농도에 대한 예측과 추세 분석
• 수위 변화 예측
• 코로나19의 종식 가능 시점과 2차 유행 가능 시점 예측
• 각종 의료비 지출을 예측하여 정책 조정의 근거 제공

동시에 연구자들은 ARIMA 모델을 개선하거나 다른 모델과 통합하였음.

• visceral leishmaniasis 예측을 위한 ARIMA-EGARCH 모델
• 디지털 텔레비전 송신기 근처 수직 경로의 전기장을 예측하기 위한 ARIMA와 신경망 기반의 하이브리드 모델
• ARIMA와 adaptive filtering 기반의 하이브리드 모델

요약하면 ARIMA 모델은 간단한 구조를 가지고 있으며, 입력되는 시계열 데이터가 stationary하거나 차분 후 stationary 해야 함. ARIMA는 선형 관계만 포착할 수 있고 비선형 관계는 포착하지 못함.

3.1.2 THE CLASSIC NONLINEAR MODELS

선형 예측 모델은 이해하기 쉽고 구현이 간단하지만, 선형 모델은 linear assumption을 전제로 구축해야 하므로 비선형 시계열 데이터에는 효율성이 떨어짐.

고전적인 비선형 모델에는 Threshold Autoregressive (TAR) 모델, Autoregressive Conditional Heteroscedasticity (ARCH) 모델, Constant Conditional Correlation (CCC) 모델 등이 있음.

Threshold Autoregressive (TAR) 모델은 different intervals의 autoregressive models를 사용하여 전체 구간의 비선형 변화 특성을 설명함.

핵심 아이디어는 관측 시퀀스 $\{x_i\}$의 값 범위에 $L-1$ 개의 임계값 $r_j(j = 1, 2, 3, ... , L-1)$을 도입하고 이를 $L$ 간격으로 나누는 것임.

number of delay steps $d$에 따라, $\{x_i\}$는 $\{x_i - d\}$ 값에 따라 다른 임계값 간격에 할당되고, 다른 간격의 $x_i$는 다른 autoregressive 모델에 의해 설명됨. 이러한 autoregressive 모델의 합은 전체 $\{x_i\}$의 비선형 dynamic 표현임.

모델 구축 단계가 복잡하고, 임계값의 수와 각 임계값을 먼저 결정해야 하기 때문에 초창기에 TAR 모델을 주로 사용되지 않았음. Tsay가 임계값 수와 임계값 추정 방법을 제시하고 나서 TAR 모델이 널리 사용됨.

TAR 모델의 파라미터는 임계값에 따라 변화됨. 임계값 변수를 시계열 자체의 delay로 선택하면 모델은 self-exciting threshold autoregressive (SETAR) 모델이라는 특수한 종류의 임계값 모델이 됨.

TAR 모델을 기반으로 한 Multivariate Threshold Autoregressive (MTAR) 모델이 제안되었으며, TAR 모델의 여러 단계 간의 discontinuous dynamic transitions 문제를 해결하기 위해 Terasvirta에 의해 평활 전이 자동 회귀 (STAR) 모델이 제안되었음.

금융 분야의 시계열 데이터는 큰 변동 뒤에는 큰 변동이, 작은 변동 뒤에는 작은 변동이 뒤따르는 등 volatility clustering의 특성을 가지고 있음. 이러한 특성을 감안하여, Engle은 조건부 분산이 과거 수익률의 제곱의 함수인 Autoregressive Conditional Heteroscedasticity (ARCH) 모델을 제안하였음.

ARCH 모델을 기반으로 generalized autoregressive conditional heteroscedasticity (GARCH) 모델이 제안되었으며, 이후로 EGARCH (Exponential GARCH) 모델, APGARCH 모델, GJR-GARCH 모델, FIGARCH 모델 등이 제안되었음.

Bollerslev는 비선형 시계열 예측을 위한 Constant Conditional Correlation (CCC) 모델을 제안하였음. CCC 모델은 조건부 공분산 행렬을 조건부 분산과 조건부 상관 행렬의 두 부분으로 분리하며, 이후 최대 우도 추정 방법을 통해 파라미터를 추정함. CCC 모델은 파라미터가 적고 조건부 분산의 positive definiteness를 보장하는 데 이점이 있음.

이후 CCC에 기반한 Dynamic Conditional Correlation (DCC) 모델이 제안되었음. DCC는 조건부 상관행렬을 모델링하고 시간에 따라 조건부 상관행렬이 변화하도록 함.

요약하면, 초기 비선형 시계열 예측에는 전통적인 비선형 예측 방법이 사용되었음. 연구자들은 특정 분야에서 더 복잡한 시계열 데이터를 처리하기 위해 일반화된 모델을 많이 제안하였음.

3.2 MACHINE LEARNING FORECASTING MODEL OF TIME SERIES

고전적인 시계열 예측 모델은 시계열의 선형 관계를 잘 포착할 수 있으며 데이터 세트가 작을 때 좋은 결과를 얻을 수 있음. 그러나 대규모의 복잡한 비선형 시계열에 적용하면 그 효과가 떨어지게 됨.

multi-layer perceptrons (MLPs) networks, radial basis function (RBF) networks는 adaptive and self-organizing learning mechanisms을 가지고 있으며 이 모델들은 비선형 시계열 예측에 사용된 가장 초기의 신경망 모델로 좋은 효과를 얻었음.

fuzzy theory, Gaussian process regression, decision tree, support vector machine, LSTM 등 다양한 모델들이 시계열 예측에 사용되며, 이 모델들은 양호한 비선형 시계열 예측 능력을 가지고 있음.

3.2.1 FUZZY TIME SERIES FORECASTING METHOD

Fuzzy time series forecasting은 비선형 문제를 해결할 수 있으며, 작은 데이터 집합 또는 결측치가 있는 데이터 집합의 시계열 예측에 자주 사용됨.

Song과 Chissom은 퍼지 집합 이론을 기반으로 퍼지 시계열 예측 방법을 제안하였음. 그 후, 계산이 복잡하고 계산 시간이 긴 문제를 해결하기 위하여 Chen은 퍼지 시계열 모델을 구축하기 위한 간단하고 효과적인 방법을 제안함.

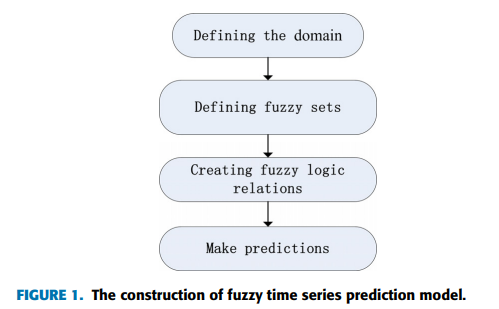
Fuzzy time series forecasting의 특성과 장점으로 인해 다양한 분야에서 연구되고 널리 활용되고 있으며, 연구자들은 모델의 정확성과 해석성을 향상시키기 위해 연구하고 있음.

3.2.2 ARTIFICIAL NEURAL NETWORK (ANN)

Artificial Neural Network (ANN)은 데이터 기반 예측 모델임. strong self-organization, self-learning and good nonlinear approximation capabilities를 가지고 있기 때문에 시계열 예측 분야에서 많은 관심을 받고 있음.

실제 훈련 데이터가 제한적이므로 ANN 모델은 과적합 현상을 보이는 경우가 많으며, 특히 소규모 데이터 학습에서는 모델의 성능 저하가 더욱 뚜렷함.

다음의 식으로 ANN을 공식화 함.

$t = f(WA' + b)$

$W$는 가중치 벡터, $A'$는 입력 벡터 $A$의 전치 벡터임. 내적을 계산한 후 비선형 변환 함수를 사용하여 최종 결과를 얻음.

ANN 모델은 현재 시계열 예측 분야에 널리 사용되고 있음. 다음과 같은 적용 예시가 있음.

• 수문 월별 유출량을 예측하기 위한 하이브리드 모델
• 폐수 유입 예측을 위한 ARIMA와 ANN의 혼합 모델

요약하면, ANN은 시계열 예측에서 좋은 결과를 얻었지만 데이터의 규모에 영향을 받아 과적합이 발생할 수 있음. 따라서 ANN은 소규모 데이터 샘플의 시계열 예측에 적합하지 않음.

또한, classic linear models와 ANN을 혼합한 혼합 모델이 단일 모델보다 예측에서 더 우수한 성능을 보이는 경우가 존재하였음.

3.2.3 GAUSSIAN PROCESS REGRESSION

Gaussian process (GP)는 Bayesian neural network를 기반으로 하는 기계 학습 방법임. GP는 확률 변수의 집합이며, 집합에 있는 임의의 변수는 joint Gaussian distribution을 따르며 평균 함수와 공분함 함수에 의해 고유하게 결정됨. 그 공식은 다음과 같음.

$\begin{cases} m(x) = E[f(x)] \\ k(x, x') = E[(f(x) - m(x))(f(x') - m(x'))] \end{cases}$

$x, x' \in R^d$는 random variable factor이고, GP는 $f(x) \sim GP(m(x), k(x, x'))$로 표현될 수 있음.

Gaussian Process Regression (GPR)은 데이터에 회귀 분석을 수행하기 위한 Gaussian Process (GP) priors를 사용한 비모수 모델임. GPR 모델 가정에는 노이즈(회귀 잔차)와 가우시간 프로세스 prior가 포함되며, 베이지안 추론에 따라 해결됨.

GPR은 compact 공간에서 임의의 연속 함수의 보편적 근사치이며, GPR은 결과를 예측하기 위해 posterior를 제공할 수 있음. likelihood가 정규 분포를 따르면, posterior는 analytical form을 가짐. 따라서, GPR은 versatility와 resolvability를 가진 확률적 모델임.

현재 Gaussian process regression 모델은 도구 손실 예측, 모집단 모델 비모수 식별, 회귀 및 분류 등 많은 분야에 적용되고 있음. 다음과 같은 추가 적용 예시가 있음.

• 월별 지하수 수위 변동 확률 예측
• 다양한 slope displacement 예측
• 배터리 상태 예측

더 나은 시계열 예측 결과를 달성하기 위해 연구자들은 GPR의 일부 개선 또는 통합 모델을 제안함. 다음과 같은 예시가 있음.

• GPR과 multiple imputation 방법을 기반으로 한 multivariate forecasting 모델
• Gaussian mixture model (GMM)과 particles swarm optimization (PSO)의 변형을 사용한 hybrid GMM-IGPR 모델
• 계산 복잡도와 예측 정확도를 향상시킨 변형 GPR 모델

요약하면, GPR(Gaussian Process Regression)은 베이지안 머신 러닝 방법임. GPR의 높은 계산 비용으로 인해 주로 저차원 및 적은 데이터의 회귀 문제에 사용됨.

또한, GPR은 모델링을 위한 매개변수가 적고 사용 가능한 커널 함수가 더 많아 ANN, SVM과 같은 방법에 비해 더 유연함.

3.2.4 SUPPORT VECTOR MACHINE

Support Vector Machine (SVM)은 작은 표본과 비선형 문제에 장점을 가진 분류 알고리즘이며, 분류, 패턴 인식, 시계열 예측 등 널리 사용되는 알고리즘임.

SVM의 핵심 아이디어는 분류 정확도를 바탕으로 최적의 초평면을 찾는 것임.

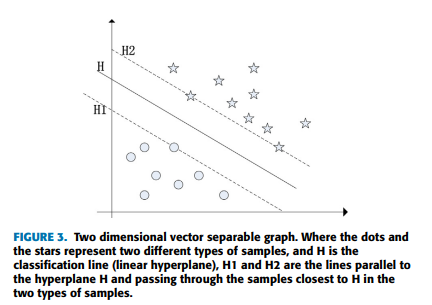
위 그림의 직선 $H$를 classification line (linear hyperplane)이라하고, $H1, H2$는 $H$와 평행하고 두 종류의 샘플에서 $H$에 가장 가까운 샘플을 통과하는 직선임. $H1$과 $H2$ 직선의 샘플을 서포트 벡터라고 함.

$H1$과 $H2$ 사이의 거리를 classification interval이라고 하며, SVM 알고리즘으로 검색할 최적의 초평면은 maximum classification interval을 가지는 $H$를 의미함.

두 클래스를 구분하는 linear discrimination 함수는 다음과 같음.

$f(x) = \omega \cdot x + b$

classification hyperplane (H)는 다음의 식으로 표현됨.

$\omega \cdot x + b = 0$

주어진 데이터들은 다음과 같이 분류될 수 있음.

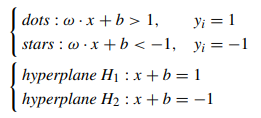
Classification interval은 $\vert H1H2 \vert = \frac{2}{\Vert \omega \Vert}$ 이고, classification interval를 최대화하는 것은 $\Vert \omega \Vert$를 최소화하는 것과 동일한 문제임.

SVM은 전통적인 시계열 예측 모델에 비해 성능이 좋지 않음. seasonal autoregressive integrated moving average (SARIMA) 모델, SVM, data processing grouping method (GMDH) 모델을 서로 비교하였을 때 SARIMA와 GMDH 모델이 SVM보다 우수한 성능을 기록하였음.

연구자들은 SVM을 다른 방법과 결합하였으며, residual-based deep least squares support vector machine (RBD-LSSVM) 등을 제안하며 비선형 시계열 모델링 및 예측에서 우수한 성능을 증명하였음.

요약하면, SVM의 주된 장점은 데이터 분류임. 분류의 경우 소규모 샘플 데이터 세트에 적합함. SVM의 계산 복잡도는 서포트 벡터의 수에 따라 결정되므로 "차원의 저주"를 피할 수 있음. 또한, 이상치에 민감하지 않아 주요 샘플을 잘 포착할 수 있으며 강건함과 일반화 성능이 좋음.

그러나 단일 SVM 모델은 시계열 예측에 효과적이지 않으며, 시계열 예측을 위해 mixed 모델이 일반적으로 사용됨.

3.2.5 RECURRENT NEURAL NETWORKS

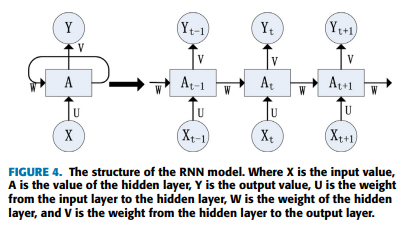
Recurrent Neural Networks (RNN)은 시퀀스 데이터를 입력으로 받아 재귀적으로 처리하고 모든 노드가 연쇄적으로 연결되어 있어 시퀀스 및 Correlation 데이터 처리에 효과적인 모델임.

RNN은 시계열에 더 민감하고 data transmission에 있어 메모리를 가지고 있음. 예를 들면, 시간 $t$에서의 입력은 시간 $t-1$의 결과를 참조함.

RNN의 그림을 보면 시간 $t$에서의 입력값, 은닉값, 출력값은 $X_t, A_t, Y_t$임을 확인할 수 있음. 현재 은닉값 $A_t$는 현재 입력값 $X_t$와 이전 순간의 은닉값 $A_{t-1}$에 의해 결정됨.

출력값 $Y_t$는 입력 $A_t$와 이전 입력 $A_{t-1}, A_{t−2}, A_{t−3}, ...$에 의해 영향을 받음. 따라서, RNN은 입력 시퀀스에 길이에 상관 없이 모든 시퀀스를 입력 받을 수 있음.

그러나, 시퀀스의 길이가 길어짐에 따라 더 깊은 네트워크와 많은 훈련 시간이 필요하게 됨. 또한, 시퀀스의 길이가 길 경우 그래디언트가 이전 시퀀스로 다시 전파되기 어려워 gradient vanishing 문제가 발생하여 long-term dependence 문제를 해결할 수 없음.

RNN의 vanishing and exploding gradient 문제를 해결하기 위하여, long short-term memory (LSTM) 모델이 제안되었음. LSTM은 RNN의 특수한 한 종류로, gradient vanishing 문제를 효과적으로 방지함.

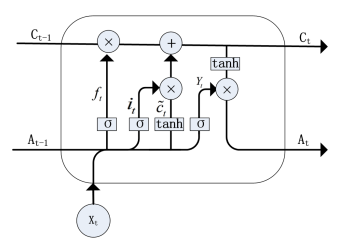
LSTM은 transmission state를 제어하기 위해 input gate, output gate, forget gate 총 3개의 gate를 사용함.

LSTM은 RNN에 비해 중요한 정보는 더 오래 기억할 수 있고, 불필요한 정보는 삭제할 수 있음. 이러한 특성을 기반으로 LSTM은 긴 시계열 예측에서 더 나은 성능을 가짐.

LSTM은 다양한 기상 변수(온도, 습도, 구름의 cover 정도 등)를 사용하여 전역 일사량 예측하는 등, 현재 시계열 예측에 널리 사용되고 있음.

또한, 연구자들은 데이터의 특성을 기반으로 LSTM을 개선하였음. 다음과 같은 예시가 있음.

• 인근 샘플의 큰 영향을 기반으로 하는 transfer LSTM (T-LSTM)
• 유전 알고리즘을 사용하여 최적화한 deep long short-term memory (DLSTM)
• AdaBoost-LSTM 앙상블 학습 등 모델 통합

요약하면, LSTM 모델은 시계열 예측 분야에서 널리 사용되고 있으며, 그래디언트 문제를 최적화하기 때문에 긴 시계열 데이터 분석에 적합함. 연구 결과에 따르면 통합 LSTM 모델의 성능이 단일 모델보다 보통 더 우수한 것으로 나타남.

3.2.6 TRANSFORMER

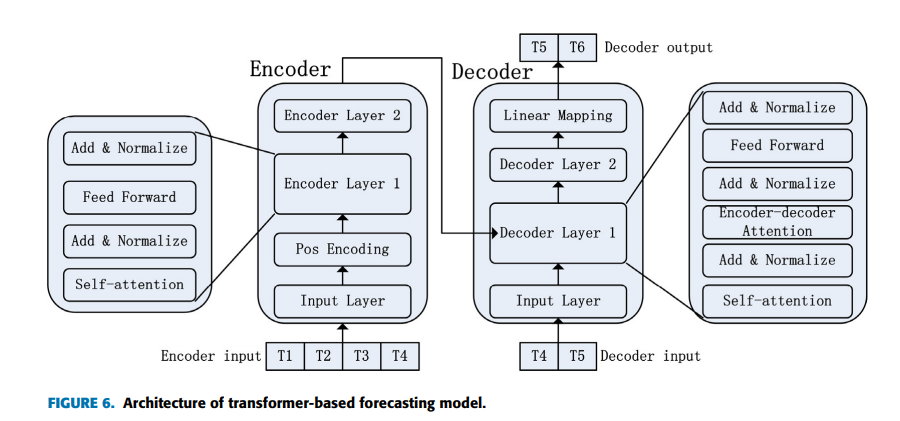
Transformer는 Google에서 제안한 NLP 모델임. RNN의 순차적 구조 대신 Self-Attention 메커니즘을 사용하여 모델을 병렬적으로 훈련하고 global information를 얻을 수 있음. Transformer의 구조는 크게 인코더와 디코더로 구성되어 있음. 인코더 부분은 과거 시계열을 입력으로 하고 디코더 부분은 자기 회귀성을 기반으로 미래 값을 예측함.

디코더는 인코더에 어텐션 메커니즘을 가지고 연결되어 있음. 이 방법으로 디코더는 예측을 하기 전에 시계열의 과거 값 중 가장 유용한 부분에 "주의를 기울이는(pay attention)" 것을 학습함. 또한 디코더는 masked self-attention를 사용함. 이 방법으로 디코더는 훈련 중에 미래 값을 얻지 못하며, 미래의 정보 유출을 피할 수 있음.

현재 Transformer는 시계열 예측 분야에서 자주 사용되고 있음. self-attention mechanisms을 사용하여 시계열 데이터의 복잡한 패턴을 학습함으로 좋은 성능을 보여줌. 또한, 시계열 임베딩뿐만 아니라 일변량 및 다변량 시계열 데이터에도 적용할 수 있음.

이외에도, 다음과 같은 Transformer의 개선 모델이 존재함.

• Generative Adversarial Networks (GANs) 기반의 Adversarial Sparse Transformer (AST). AST는 Sparse Transformer를 generator로 사용하여 시계열 예측을 위한 sparse attention map을 학습하고, 시퀀스 레벨의 예측 성능을 높이기 위해 discriminator를 사용함
• 데이터 불균형 문제를 완화하기 위해 main embedding space를 사용하여 시간과 공간에 걸친 상호 의존성을 포착하는 hierarchically structured Spatial-Temporal Transformer network (STtrans)

요약하면, Transformer는 시계열 예측에 사용되며 좋은 결과를 얻었음. Transformer는 시계열 간의 복잡한 의존 관계를 잘 포착할 수 있고 병렬로 계산할 수 있음. 그러나 Transformer는 시퀀스 간의 long-distance information을 포착할 수 없고 계산량이 많음.

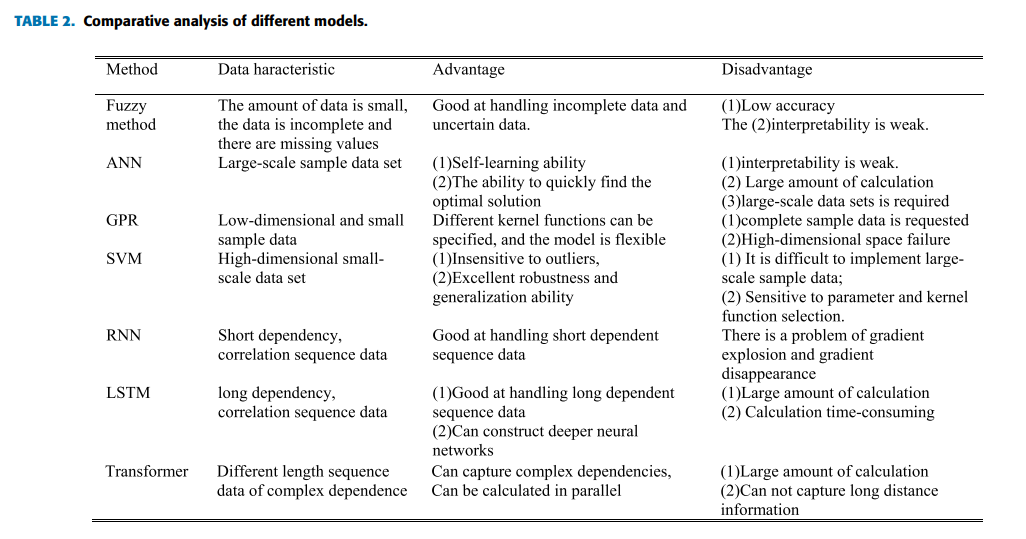
아래 TABLE 2는 서로 다른 기계 학습 방법론의 특성을 정리한 것임.

3.3 HYBIRD FORECASTING MODEL

시계열 예측 분야에서는 고전적인 방법과 기계 학습의 예측 방법이 각각의 장점을 가지고 있음. 실시간 시계열 데이터에는 다음과 같은 특성이 있어, 하나의 모델만을 선택하기 어려움이 있음.

• 시계열 데이터가 선형인지 비선형인지 판단하기 어렵고, 데이터에 대한 특정 모델의 타당성 판단이 불가능할 수 있음
• 실제로, 순수하게 선형이거나 비선형인 시계열 데이터는 거의 없으며, 시계열 데이터는 일반적으로 선형 데이터와 비선형 데이터의 조합임.
• 하나의 모델이 모든 상황에 적합할 수 없음. 단일 모델로는 서로 다른 시계열 패턴을 동시에 포착할 수 없음.

따라서, 데이터의 서로 다른 분포 패턴을 포착하기 위해 고전적인 방법과 머신 러닝을 결합한 하이브리드 모델이 발전 추세에 있음. 하이브리드 모델은 시계열의 복잡한 분포 패턴을 포착할 수 있으며, 모델의 정확성과 일반화 성능을 향상시킬 수 있음.

3.3.1 HYBRID MODEL BASED ON ARMA AND MACHINE LEARNING

ARMA와 머신러닝을 결합한 하이브리드 알고리즘은 다양한 분야에 적용되어 좋은 성과를 거두었음.

ARMA 모델과 PSO-SVM(particle swarm optimization SVM) 모델 기반의 clustering hybrid prediction model: C-PSO-SVM-ARMA 모델이 제안되었으며, 높은 연산 효율과 예측 성능을 가짐을 실험으로 확인하였음.

추가로, EMD-GM-ARMA, VMD-PRBF-ARMA-E 등 예측 정확도가 더 높은 ARMA 기반 하이브리드 모델들이 제안되었음.

3.3.2 HYBRID MODEL BASED ON ARIMA AND MACHINE LEARNING

ARIMA와 머신 러닝을 결합한 하이브리드 방법 또한 시계열 예측 분야에서 널리 사용됨. 다음과 같은 예시가 있음.

• primary energy consumption economy 예측을 위한 integrated empirical mode decomposition (EEMD) 기반의 EEMD-ARIMA-GA-SVR 모델
• 강우량 예측을 위한 SSA-ARIM-ANN 모델. ARIMA는 stationary 성분을, ANN은 non-stationary 성분을 모델링함.
• dense urban forest 지역의 전자기파의 전파를 예측하기 위한 ARIMA, ANN 기반의 하이브리드 모델
• global solar 예측을 위한 non-linear AR, ANN 기반의 하이브리드 모델
• 옥수수 가격 예측을 위한 ARIMA, SVM 기반의 하이브리드 모델
• 병원 내 외래 방문 횟수 예측을 위한 ARIMA, LSTM 기반의 하이브리드 모델
• hydrological time series 예측을 위한 wavelet denoising, ARIMA-LSTM 기반의 하이브리드 모델

3.3.3 HYBRID MODEL BASED ON MACHINE LEARNING

연구자들은 머신러닝과 딥러닝 기반의 통합 모델을 제안하였고, 실제 애플리케이션에 매우 잘 작동함을 입증하였음. 다음과 같은 예시가 있음.

• 단기 부하 예측을 위한 CNN, SVM 기반의 하이브리드 모델
• 금의 가격과 추세를 예측하기 위한 CNN-LSTM 모델

빅데이터의 발달로 여러 분야에서 방대한 시계열 데이터가 빠르게 생산되고 있으며, 데이터는 복잡한 비선형 데이터로 서로 다른 분포 패턴을 따름. 복잡한 시계열 데이터를 단순 통계 모델이나 머신 러닝 모델로 처리할 경우 예측 성능이 떨어지고 일반화 성능이 부족함.

단일 모델보다는 하이브리드 모델이 정확도와 일반화 성능 면에서 더 우수하기 때문에 어떤 모델이 적합한지 모를 때는 하이브리드 시계열 예측 모델이 가장 좋은 선택이 될 수 있음.

이 외에도 complex networks에 기반한 시계열 분석 모델, fuzzy interval time-series forecasting 모델 등 시계열 분석을 위한 다른 흥미로운 알고리즘들이 존재함.

4. FUTURE DIRECTIONS AND OPEN ISSUES

최근 시계열 예측 연구가 큰 성과를 거두고 있지만, 데이터 규모의 급속한 성장과 복잡한 시계열 데이터의 생성으로 인해 기존 예측 방법에 큰 어려움이 초래되고 예측 방법의 계산 효율성에 영향을 미치고 있음.

향후 시계열 예측 연구의 잠재적 연구 방향과 동향을 몇 가지로 정리하면 다음과 같음.

4.1 DATA PREPROCESSING

대량의 시계열 데이터를 생성하는 과정에서 일부 누락된 데이터가 있을 수 있음. 결측 데이터 문제에 대한 일반적인 방법은 위의 TABLE 3와 같음. 이러한 방법들은 대개 인접한 시계열 데이터 간의 상관관계를 무시함. 데이터를 맹목적으로 채울 경우 표본 데이터의 분포 패턴을 파괴할 수 있음.

딥러닝은 샘플 데이터의 패턴 분포 정보를 캡처하고 샘플 데이터의 패턴 정보를 기반으로 누락된 데이터를 보완하는 효과적인 방법이 될 수 있음.

예를 들어, generative adversarial neural network를 기반으로 표본 데이터 분포 패턴에 따라 결측 데이터를 채우면 원래 데이터와 가능한 한 유사한 완전한 시계열을 얻을 수 있으므로 이후 시계열 분석 작업에 도움이 될 것임.

현재 시계열에서 누락된 값을 채우기 위한 정밀하고 효율적인 방법을 찾지 못하였음. 시계열 데이터 분석의 필요성과 함께, 원본 데이터 분포 패턴을 기반으로 누락된 값을 채우는 것은 매우 유망한 연구 분야가 될 것으로 생각함.

4.2 MODEL CONSTRUCTION

Real-time incremental data의 특성을 모델과 결합하여 모델의 정확성과 강건성을 향상시킬 수 있음.

현재 사람들은 주로 과거의 시계열 데이터를 기반으로 예측 모델을 구축하여 미래의 데이터 예측에 활용하고 있음. 그러나, 시간의 흐름과 다양한 objective factor의 영향으로 새로운 데이터의 특성과 분포 패턴을 바탕으로 모델을 수정하여 정확성과 강건성을 높일 필요가 있음.

그렇지 않으면 시간이 지남에 따라 모델의 예측 정확도와 성능이 우리의 요구를 충족시키지 못할 것임. incremental data를 기반으로 수정된 시계열 예측 모델은 잠재적인 연구 방향이 될 것임.

현재까지 online incremental data를 기반으로 한 수정된 시계열 예측 모델을 찾지 못하였음. 대규모 시계열이 축적되고 예측 분석에 대한 수요가 증가함에 따라 매우 유망한 연구 분야가 될 것으로 판단됨.

4.3 PARALLEL COMPUTING

시계열 데이터의 급속한 성장에 따라 컴퓨팅 자원이 한계에 도달하고 실시간 예측 분석을 구현할 수 없다는 문제가 생김. 따라서, 빅데이터 기술 기반의 시계열 데이터 병렬 컴퓨팅은 잠재적인 연구 방향이 될 것임.

5. CONCLUSION

빅데이터 시대의 발전에 따라 시계열 데이터를 기반으로 한 예측 연구가 각광받고 있음. 다양한 분야에서 점점 더 많은 시계열 데이터가 생산되고 있으며, 이는 시계열 분석 분야의 발전을 촉진하고 있음.

대규모 시계열 데이터의 복잡한 패턴 분포로 인해 보다 나은 예측 정확도와 성능을 얻기 위해 하이브리드 예측 모델을 기반으로 복잡한 시계열 분포 패턴을 포착하는 연구자들이 증가하고 있음.

본 논문에서는 먼저 시계열의 개념을 제시하고, 현재 시계열 예측 연구 분야에서의 관련 이슈를 정리한 후 분류별로 시계열 예측 방법을 소개하였음. 또한, 데이터 전처리, incremental data 모델, 병렬 컴퓨팅 등 몇 가지 잠재적인 연구 방향과 해결되지 않은 문제를 정리하였음.

기존 시계열 예측 방법에 대한 종합적인 조사를 통해 시계열 예측 분야 연구에 참고가 될 것으로 기대함.