
본 포스팅은 제가 읽었던 논문을 간단하게 정리하는 글입니다. 논문의 모든 내용을 작성하는 것이 아닌, 일부분만 담겨 있으므로 자세한 내용은 원본 논문을 확인해 주시기를 바랍니다. 또한, 논문을 잘못 이해한 부분이 있을 수 있으므로, 양해 바랍니다.
Overview
본 논문에서는 image tag(label)만 주어진 상황에서 object detection task를 수행하는 Weakly Supervised Object Detection(WSOD) task를 다룸.
지금까지 WSOD 분야에 많은 발전이 있었지만, 해결해야 할 여러 문제가 아직 남아있음. 이전 Pseudo Mask Generation 논문에서도 언급하였지만, CNN 모델의 경우 가장 discriminative feature에 집중하는 경향이 있으므로 아래 왼쪽의 그림처럼 객체의 일부(박스 A)만을 중요하게 여길 수 있음.

바람직한 detection box는 오른쪽의 D임. 객체만을 포함하는 최대의 bounding box를 찾아야 함. 본 논문에서는 multi-stage refinement 과정을 추가하여 이를 구현하고자 함.
아래의 이미지를 통해 여러 번의 refinement 과정이 수행됨에 따라 객체 탐지 결과가 어떻게 달라지는지 확인할 수 있음.

Method
아래 이미지는 논문에서 제안하는 아키텍처를 설명함.
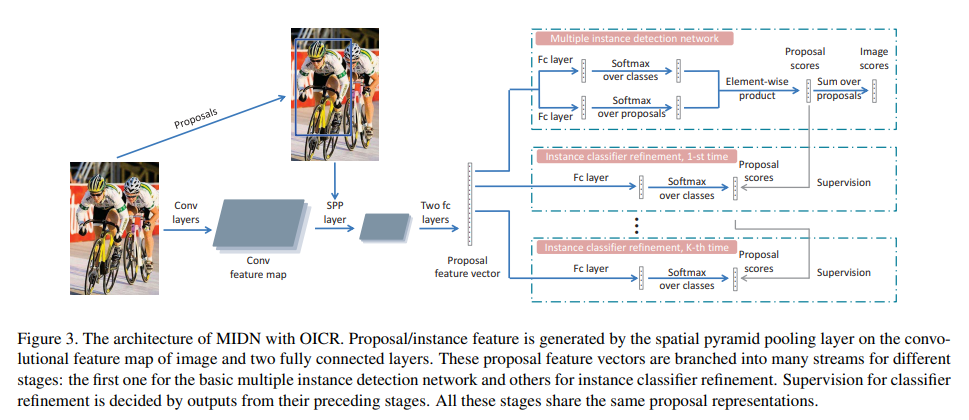
본 논문에서 제안하는 아키텍처는 크게 두 가지의 단계로 이루어져 있음. 첫 번째 단계는 Multiple Instance Detection Network(MIDN) 단계, 두 번째 단계는 Online Instance Classifier Refinement(OICR) 단계임.
기존 object detection의 Fast R-CNN과 같이, 입력 이미지 내의 ROI를 찾기 위해 Selective Search(SS)를 사용하였음. SS를 통해 2,000개의 object proposals를 얻으며, 이후 Spatial Pyramid Pooling(SPP) layer를 사용하여 각 proposal을 고정된 길이의 벡터로 변환함. 고정된 길이로 변환된 벡터는 이후 2개의 fully connected(fc) layer를 거친 후(proposal feature vector) MIDN과 OICR로 입력됨.
여러 개의 단계(stage)를 가지는 OICR의 경우, 이전 단계의 출력을 supervision 정보로 사용함. 첫 번째 stage의 경우 MIDN의 출력 값을 사용함.
supervision of refined classifier depends on outputs from th refined classifier.
본 논문에서의 핵심 아이디어는 top-scoring proposal과 해당 proposal과 인접한 proposal은 동일한 label(image tag)로 생각할 수 있다는 것임.
Multiple Instance Detection Network
본 논문에서는 MIDN을 basic instance classifier로 표현하기도 하였음.
MIDN는 2가지의 branch를 가지고 있으며, fc layer를 통해 각각 을 계산함. 는 전체 클래스 개수를 의미하며 는 proposal의 개수(2,000)를 의미함.
다음으로 에 softmax 함수를 적용하며, 함수를 적용하는 방향(axis)을 다르게 함.
의 경우 proposal 의 클래스 확률 분포를 의미하며(proposal 는 어떤 클래스에 속하는지), 의 경우 클래스 에 대한 proposal 확률 분포를 의미함(클래스 는 어떤 proposal에 속하는지).
계산된 두 결과를 element-wise product하여 proposal score를 계산함.
클래스 c에 대한 image score 는 전체 proposal의 합으로 계산됨. 는 (0, 1) 사이 값을 가짐.
이미지 레이블의 경우, 해당 이미지 안에 특정 객체가 포함되어 있는지를 나타냄. 이미지 레이블은 아래와 같이 주어짐. 클래스 가 존재하면 임.
계산된 proposal score와 이미지 레이블을 기반으로 MIDN의 loss를 계산함. 가 높을수록 네트워크는 해당 클래스 가 입력 이미지 내에 존재한다고 더욱 확신함. 따라서 와 이미지 레이블 를 사용하여 cross-entropy loss를 계산할 수 있음.
Online Instance Classifier Refinement
MIDN에서 계산된 결과만으로는 객체의 위치를 추정하기에는 부족한 부분이 많음. Figure 2. 의 가장 첫 번째 row와 같이 객체의 위치를 전부 포착하지 못하는 문제가 발생할 수 있음. 전체적인 객체의 위치를 찾아낼 수 있도록, Multi-stage classifier refinement 과정을 수행함.
stage에서 proposal 의 output score vector를 라 하면, 는 차원의 벡터임.
는 번째 refinement stage를 의미하며, 는 전체 refinement 횟수를 의미함. 번째 클래스는 background에 대한 클래스임. 일 때의 output score vector는 MIDN의 출력 값을 사용함. Output score vector는 proposal feature vector를 하나의 fc에 입력하여 얻음.
stage에서, 하나의 proposal 에 대한 label vector 는 이전 stage의 출력 값을 기반으로 생성함. stage에서, 클래스 에 대한 highest score proposal()을 계산함(이미지 내 클래스 가 존재한다고 가정).
Proposal 의 경우 클래스 일 확률이 가장 높기에, 해당 proposal의 클래스를 로 설정함.
비슷한 영역을 포함하는 proposal은 같은 클래스일 확률이 높으므로, proposal 과 많이 겹치는(high overlap) proposal 또한 클래스 로 설정함. 즉, 과 과 인접한 proposal의 stage label을 로 설정함. Proposal 간 겹치는 정도는 두 proposal 사이의 IoU를 사용하며, 본 논문에서는 실험적으로 결정된 threshold 를 사용함.
어떤 클래스의 top scoring proposal과도 겹치지 않은 proposal은 background로 설정되며, 해당 이미지 내 클래스 가 없다면 모든 를 0으로 설정함.
이러한 제약 사항을 고려하여, 아래의 loss function을 사용할 수 있음. 여러 번의 refinement 과정을 통해 detector는 객체의 더 큰 부분을 점진적으로 탐지할 수 있음.
학습 초반의 refining classifier는 매우 noisy 할 수 있으며, 결과적으로 unstable solution을 얻을 수 있음. 이를 고려하여 위의 loss function에 가중치 를 추가함.
학습 초기에는 이 작아 loss 또한 작아 unstable solution을 회피할 수 있음.
최종적으로 모든 loss function을 더하여 최종 loss를 얻을 수 있음.
아래는 본 논문에서 제안하는 OICR의 알고리즘 설명임.

Line 6
이미지 내 클래스 가 있다면 아래의 과정을 수행
Line 9
Proposal 과 top-scoring proposal 사이의 IoU 계산
Line 10, 11
에는 Proposal 과 top-scoring proposal 사이의 최대 IoU가 저장되며, 그때의 확률 값()을 가중치 로 사용
Line 12, 13
이 threshold 보다 크다면 해당 proposal의 레이블을 로 설정
Top-scoring proposal과 인접한 proposal이 하나의 class로 지정되므로, 다음 stage의 classifier는 인접하는 영역을 모두 포함하는(더 넓은) proposal을 선택하게 됨. 이 과정을 통해 객체의 더 넓은 부분을 점진적으로 찾아낼 수 있음.
Experiments
Experimental setup
PASCAL VOC 2007, 2012 데이터셋에서 실험을 수행하였음. 평가 지표로 mAP(mean of Average Precision)와 CorLoc(Correct Localization)을 사용하였음.
ImageNet에서 pre-train 된 VGG_M과 VGG16을 사용하였으며, 각 모델의 마지막 max-pooling layer를 SPP layer로 교체한 후 fc layer를 추가하였음. 마지막 feature map 크기를 키우기 위해 dilated conv layer 등을 사용하였음. Total refinement times 는 3으로 설정하였음.
추가적인 모델 세팅은 원본 논문을 참고.
Ablation experiments
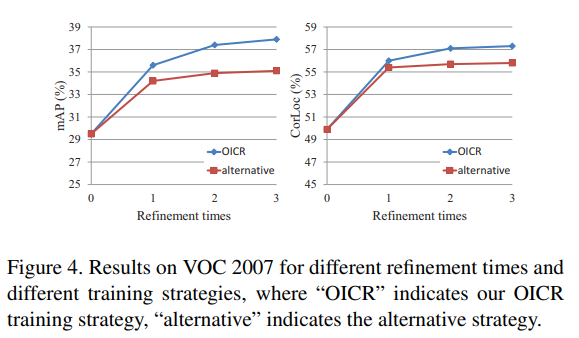
본 논문에서 제안하는 OICR 과정을 진행했을 때, 단 한 번의 refinement 과정만으로도 모델의 성능이 향상되는 것을 확인할 수 있었음.
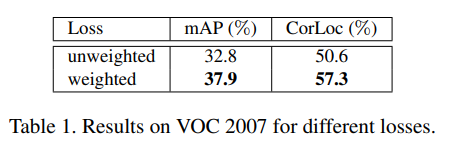
학습 초기의 불안정함을 조절하기 위한 가중치 를 추가하였을 때, 모델의 성능이 향상됨을 확인하였음.
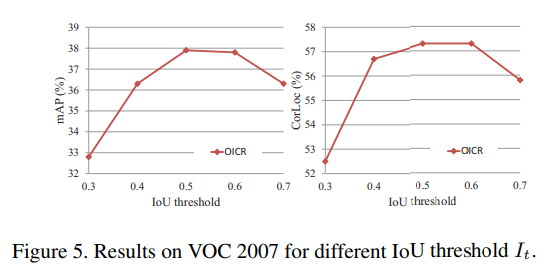
실험적으로, threshold 는 0.5일 때 가장 좋은 성능을 달성함을 확인하였음.
추가적인 실험 결과 및 한계점은 원본 논문을 참고.
