WSOD2 : Learning Bottom-up and Top-down Objectness Distillation for Weakly-supervised Object Detection
논문 정리

본 포스팅은 제가 읽었던 논문을 간단하게 정리하는 글입니다. 논문의 모든 내용을 작성하는 것이 아닌, 일부분만 담겨 있으므로 자세한 내용은 원본 논문을 확인해 주시기를 바랍니다. 또한, 논문을 잘못 이해한 부분이 있을 수 있으므로, 양해 바랍니다.
Overview

지금까지 Weakly-supervised Object Detection(WSOD)에는 CNN 기반의 classification 모델을 사용하여 객체의 위치를 추정하였음. OICR, PCL 등 WSOD를 위한 다양한 아키텍처가 제안되었으나, 위의 Figure 1과 같이 객체의 bounding box(bbox)가 작거나(partial) 너무 큰(oversized) 문제가 발생하였음.
이러한 문제가 발생하는 이유 중 하나는 이전 논문들에서 언급하였듯 CNN 모델이 가장 discriminative feature에 집중하기 때문임. Classification 모델은 종종 객체의 존재 여부에만 집중하기 때문에, 객체의 위치, 크기, 객체의 수 등을 탐지하는 것에는 어려움이 있을 수 있음.
However, a classification model often targets at detecting the existence of objects for a category, while it is not able to predict the location, size and the number of objects in images.
지금까지의 WSOD 관련 많은 연구들은 CNN의 feature map을 기반으로 객체의 boundary를 탐지하였음. 본 논문에서는 이러한 방식을 top-down fashion이라고 명명함. Top-down classifier인 CNN은 주어진 이미지에서 discriminative feature를 매우 잘 찾아내지만, 해당 feature만으로는 객체의 위치(bbox)를 정확히 찾아내기는 어려움.
CNN 이전에도 객체의 존재를 확인하려는 다양한 연구가 있었음. What is an object? 논문에서는 Multi-scale Saliency, Color Contrast, Edge Density, Superpixels Straddling 등 low-level feature를 사용하여 특정 영역 내 객체가 존재하는 정도(objectness)를 측정하였음. 본 논문에서는 이러한 low-level feature를 bottom-up evidence라 명명함.
본 논문에서는 WSOD를 위한 프레임워크 를 제안함(WSOD framework with Objectness Distillation). WSOD2에서는 bottom-up evidence와 top-down CNN을 결합하여 보다 정확한 객체의 위치를 추정할 수 있음. 해당 연구는 WSOD task에 bottom-up evidence를 사용한 최초의 연구임.
Approach
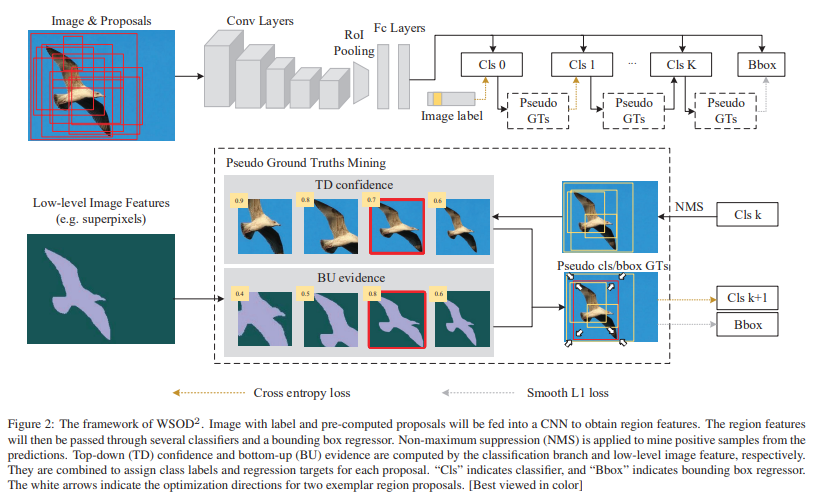
Figure 2를 통해 WSOD2의 전체적인 구조를 확인할 수 있음. 지난 OICR 논문에서와 같이 multiple instance detector(Cls 0)과 개의 refinement classifier(Cls 1 ~ Cls K)를 확인할 수 있음.
Cls 0을 사용하여 initial detected object bounding을 얻고, 각 proposal 마다 계산된 bottom-up evidence를 사용하여 번의 refinement stage를 통해 보다 정확한 bbox를 얻음.
Based Multiple Instance Detector
Based Multiple Instance Detector(MID)는 OICR 논문의 MIDN과 동일함. Selective Search(SS)를 통해 개의 region proposal을 얻고, CNN backbone을 사용하여 해당 region에 대한 feature 를 얻음.
는 두 개의 fc layer를 지난 후, 두 개의 feature matrix 로 계산됨. 는 클래스의 개수, 은 proposal의 개수를 의미함.
이후 2개의 softmax 함수가 에 적용되어, 아래의 값을 얻음.
의 경우 proposal 의 클래스 확률 분포를 의미하며(proposal 는 어떤 클래스에 속하는지), 의 경우 클래스 에 대한 proposal 확률 분포를 의미함(클래스 는 어떤 proposal에 속하는지).
계산된 두 결과를 element-wise product하여 proposal score를 계산함.
클래스 에 대한 image-level score 는 전체 proposal의 합으로 계산됨. 는 (0, 1) 사이 값을 가짐.
가 높을수록 MID Network는 해당 클래스 가 입력 이미지 내에 존재한다고 더욱 확신함. 따라서 와 이미지 레이블 를 사용하여 cross-entropy loss를 계산할 수 있음.
은 이미지 내에 클래스가 존재하는 것을 의미함.
Bottom-up and Top-Down Objectness
CNN 모델의 출력 값, classification confidence를 objectness score로 사용할 수 있음. 하지만, 이러한 Top-down 정보(confidence)만으로는 객체의 위치를 정확히 찾아내기는 어려움.
객체가 잘 정의된 경계와 중심을 가지므로, 정확히 맞는 bbox는 더 크거나 작은 bbox에 비해 보다 높은 objectness score를 가질 것이라 예상할 수 있음. Bottom-up evidence는 객체의 boundary 정보를 요약하므로, CNN 기반의 top-down feature의 부족한 부분을 보완할 수 있음.
Bottom-up evidence - Superpixels Straddling
이번 섹션의 내용은 Bottom-up evidence에 대한 이해를 높이고자 What is an object? 논문의 내용을 일부 가져온 것임. 해당 논문에서는 4가지의 low-feature를 다루나, 이후 실험에서 가장 좋은 성능을 보였던 Superpixels Straddling에 대해서만 알아봄.
Superpixel이란, 비슷한 pixel끼리 묶어 커다란 pixel을 만드는 것을 의미함. 아래의 이미지를 보면 쉽게 이해할 수 있음.

[이미지 출처]
이러한 superpixel을 활용하여, 특정 영역 내 객체가 존재하는 정도를 측정하는 방법이 바로 Superpixels Straddling(SS)임. SS는 다음의 식으로 계산됨.
는 segmentation scale 를 사용하여 얻은 superpixel의 집합을 의미함. 각각의 superpixel 마다, 영역 안에 속하는 넓이 , 영역 밖에 속하는 넓이 를 계산함.
직관적으로 생각했을 때, 객체가 어떤 영역 에 완전히 속해있다면 값은 크게 계산됨. 객체를 포함하는 superpixel 의 값이 0이 되기 때문임. 반대로, 특정 영역 가 객체의 절반만을 포함한다면, 값이 모두 존재하므로 값이 작아지게 됨.
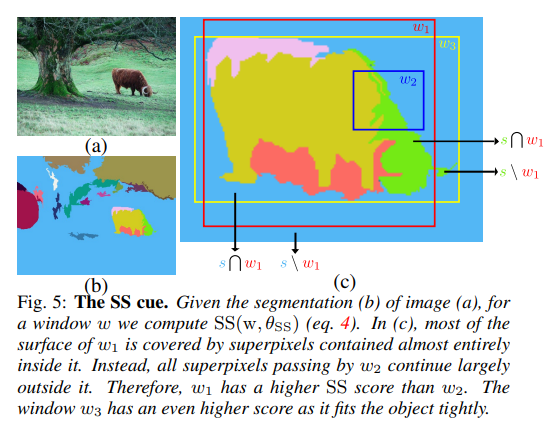
Fig. 5를 보면, 영역 에 대한 SS를 확인할 수 있음. 의 경우 값이 작게 계산되며, superpixel을 완전히 포함하는 의 경우 값이 크게 계산될 것임.
논문에서는 SS 외에도 Multi-scale Saliency, Color Contrast, Edge Density 방법을 소개함. 자세한 것은 해당 논문 참고.
Refinement Stage
다시 WSOD로 돌아와서, OICR 논문에서와 같이 번의 refinement를 수행함. Refinement 과정을 수행할 때 앞서 설명한 bottom-up evidence를 활용함.
개의 instance classifier를 정의한 후, output을 supervision으로 사용함. 각 classifier는 fc layer 이후 카테고리에 대한 softmax layer로 연결됨. 0번째 클래스를 background로 정의함.
classifier는 다음의 loss function으로 refinement 작업을 수행함.
은 proposal 에 대한 차원의 output class probability이며, 은 proposal 의 ground truth one-hot label vector임. 는 일반적인 cross-entropy 함수를 의미함.
각 proposal 에 대한 label이 존재하지 않으므로, 훈련 과정에서 pseudo ground truth label을 생성함. 이 생성 과정은 아래에서 자세히 설명함.
은 proposal 의 objectness에 대한 가중치를 의미함. 에 객체가 있을 확률이 높을수록 가중치 값이 증가함. 은 아래의 식으로 계산됨.
는 proposal 에 대한 bottom-up evidence이며, 본 논문에서는 Superpixels Straddling(SS)을 사용하였음. 는 classifier에서 생성된 proposal 의 class confidence(top-down confidence)를 의미함. 아래의 식으로 계산됨.
지난 stage의 출력 값 을 사용함. 은 생성된 pseudo label이며, one-hot vector이므로 계산에는 하나의 값만이 사용됨.
Proposal 에 대해, 가장 높은 confidence를 가지는 class의 확률 값을 사용한다고 이해하시면 됩니다.
Proposal 에 대해 얻은 bottom-up evidence 과 top-down confidence 값을 조합하여 가중치 을 계산함. 가 커질수록 bottom-up evidence를 더 많이 사용함. 본 논문에서는 값을 점점 줄여가며 top-down confidence의 영향이 커지도록 설정하였음.
Bounding Box Regression
번의 refinement 과정이 끝나면 마지막으로 output을 사용하여 bbox regression을 수행함. 비록 bbox에 대한 label 정보는 존재하지 않지만, WSOD task에서 pseudo ground truth 기반의 bbox regression을 사용하여 성능을 향상시켰던 연구가 다수 존재함.
본 논문에서는 Fast R-CNN의 bbox regressor를 사용하였음.
Fast R-CNN - Bounding Box Regressor
Ground truth bbox를 , 계산된 bbox를 라고 하면, Bbox regression의 목표는 를 에 가깝게 이동시키는 함수 를 찾는 것임.
Transformation 함수 는 다음과 같이 정의함.
는 학습 가능한 가중치이며, 는 conv layer의 출력 feature map을 의미함.
학습된 를 기반으로, Bbox 를 다음과 같이 이동시킴.
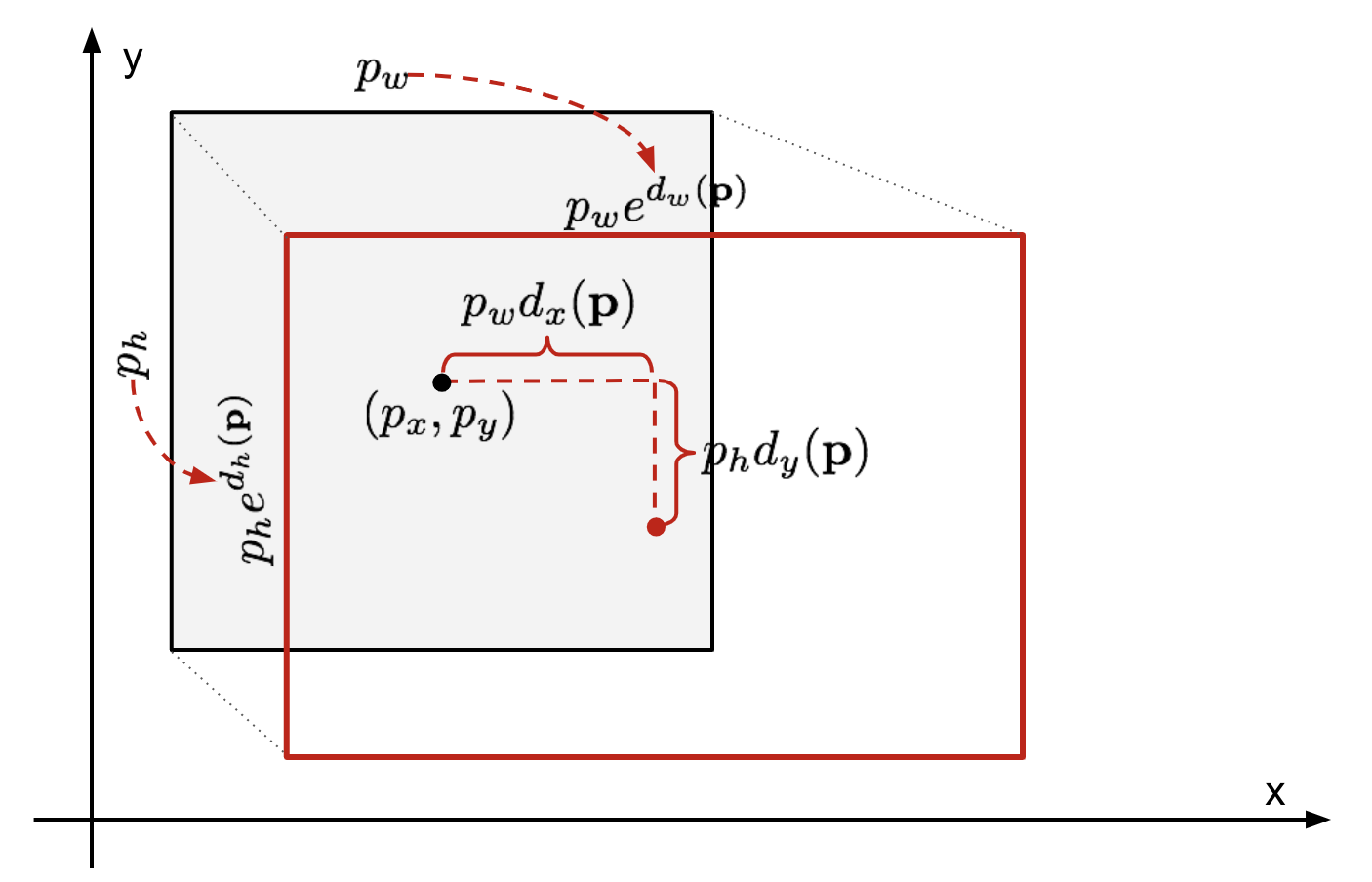
[이미지 출처]
이때, target offset은 다음과 같이 정의됨.
각 proposal 에 대하여, 이 이동해야 하는 정도(offset)인 을 정의한 후 이 값을 target으로 설정함. Bbox regression을 위해 아래의 loss를 추가함.
은 다음의 함수를 의미함.
Fast R-CNN과 다른 것이 있다면, WSOD에서는 bbox의 ground truth가 없다는 것임. 은 과 사이의 차이를 의미하며, 은 pseudo regression reference를 의미함. 는 positive(non-background) proposal을 의미하며, 이를 계산하는 방법은 아래에서 설명함.
Pseudo regression reference 은 번째 가중치 를 기반으로 결정됨. 는 refinement stage에서, proposal 의 objectness를 의미함. 아래의 식을 통해 을 결정함.
Reference 후보 proposal 은 에 속함. 과 이상 겹치는 중에서, objectness 이 가장 큰 proposal을 의 pseudo regression reference로 사용함. 즉, 각 proposal 이 근처의 objectness가 가장 높은 proposal 으로 이동하도록 학습됨.
훈련 도중, bbox regression 결과를 가중치 계산에 사용할 수 있도록 계산 식을 다음과 같이 수정함.
은 에 의해 이동된 을 의미함. 의 경우, RoI feature warping 연산이 존재하므로 proposal 을 바꾸지 않았음.
Objectness Distillation
이번 섹션에서는 pseudo ground truth label을 생성하는 방법, 를 얻는 방법 등에 대해서 다룸.
Objectness Distillation
훈련 초기에는, top-down classifier의 성능이 좋지 않으므로 bottom-up evidence가 dominant 하기를 바람. Bottom-up evidence의 지도에 따라, CNN은 top-down classifier의 confidence 분포를 조절함. 논문의 저자들은 이러한 과정을 objectness distillation이라 명명함.
훈련이 진행되고 의 신뢰성이 증가하면, 는 의 boundary decision ability를 상속받음. 따라서, 값을 점진적으로 줄여 top-down confidence에 더욱 집중하도록 조절함. 논문에서는 다양한 weight decay function을 사용하여 를 조절하였음.
Pseudo Labels
Pseudo ground truth 는 다음의 단계를 통해 이전 output을 기반으로 생성됨.
- 전체 proposal set 에 Non-Maximum Suppresion(NMS)를 적용함. 사전 정의된 임계값 를 사용하며, 각 proposal 에 대해 이전에 계산된 class probability 을 사용함. NMS 이후 남은 proposal 집합을 이라 명명.
- Background가 아닌 클래스 에 대하여 다음을 계산함. 이미지 내 클래스 가 있을 경우() 에서 에 대한 class confidence가 보다 큰 proposal을 찾고, 해당 proposal의 label을 로 설정함. 보다 큰 proposal이 없다면 highest score를 가지는 하나의 proposal의 label을 로 설정함. 이렇게 찾은 proposal의 집합을 이라 명명.
- 의 proposal(seed proposal)과 가까운 이웃 proposal을 찾음. IoU 값이 보다 높은 이웃 proposal을 찾고, 이 집합을 로 설정함. 모든 이웃 proposal은 seed proposal과 동일한 클래스 레이블을 가짐. 선택되지 못한 non-seed, non-neighbor proposal은 background로 여겨짐. 이 정보를 기반으로 one-hot label vector 을 계산함.
- 과 를 positive proposal로 정의함. 즉, .
계산 시 사용했던 함수 은 refinement stage에서 positive proposal set 를 반환하는 함수임.
Training and Inference Details
Overall learning target은 아래와 같이 표현됨.
는 하이퍼파라미터로, 본 논문에서는 을 사용하였음.
Classifier를 일차적으로 훈련시키기 위하여 초기 2,000번의 epoch 동안에는 으로 설정하였으며, 이후 값을 조정하였음. 를 사용하였음.
모델 훈련 이후, 추론 환경에서는 각 proposal에 대한 개의 출력 값을 평균 내어 class confidence를 계산하고, bbox regression을 진행함. 마지막으로, NMS(임계값 0.3)을 적용하여 중복되는 box를 제거하여 최종 추론 결과를 얻음.
Experiments
Experimental Setup
PASCAL VOC 2007 & 2012, MS COCO 데이터셋에서 실험을 진행하였음. 성능 지표로는 mean average precision(mAP)와 correct localization(CorLoc)을 사용함.
ImageNet에서 pre-trained 된 VGG16을 backbone으로 사용하였으며, Selective Search를 사용하여 각 이미지마다 약 2,000개의 proposal을 추출하였음. 추가적인 실험 세팅은 원본 논문을 참고.
Ablation Study
Bottom-up evidences
를 계산하는 방법을 다르게 하며 모델의 성능을 실험하였음. Multi-scale Saliency(MS), Color Constrast(CC), Edge Density(ED), Superpixels Straddling(SS)을 사용하였으며 각 방법의 하이퍼파라미터는 논문을 참고. 이 실험을 진행할 때는 로 설정하여 bottom-up evidence의 정보만을 활용하였음.
실험 결과는 아래와 같음.

Bottom-up evidence를 사용하였을 때, N/A 대비 유의미한 성능 향상이 있음을 확인하였음.
Impact factor α
Weight decay function을 다르게 하며 모델의 성능을 실험하였음.

Bottom-up evidence를 사용할 때, 으로 고정되었을 때(Bottom-up evidence를 사용하지 않음) 보다 유의미한 성능 향상이 있음을 확인하였음.
Effect of each component
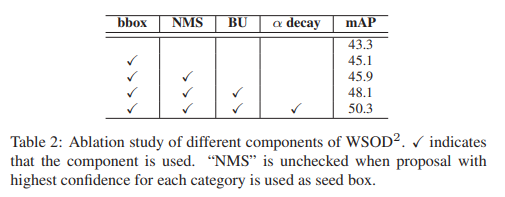
각 component의 효과를 확인할 수 있음.
Comparisons with State-of-the-Arts
다른 WSOD 아키텍처와의 성능 비교를 수행한 결과는 아래와 같음.
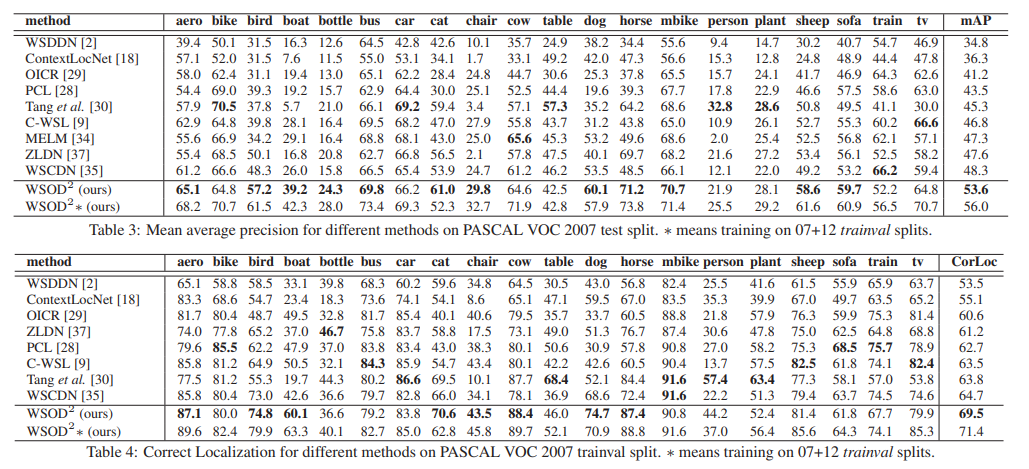
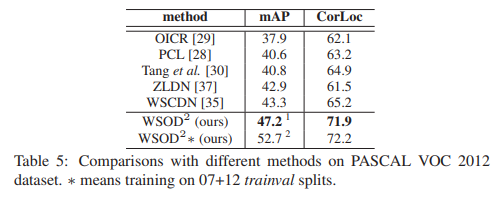
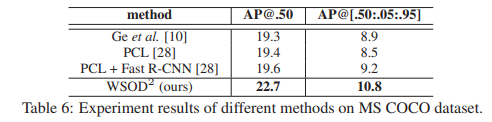
다른 아키텍처 대비 유의미한 성능 향상을 확인할 수 있음.
Visualization and Case Study
conv5 layer의 feature map을 시각화하여 WSOD2의 객체 탐지 능력을 질적으로 평가함.
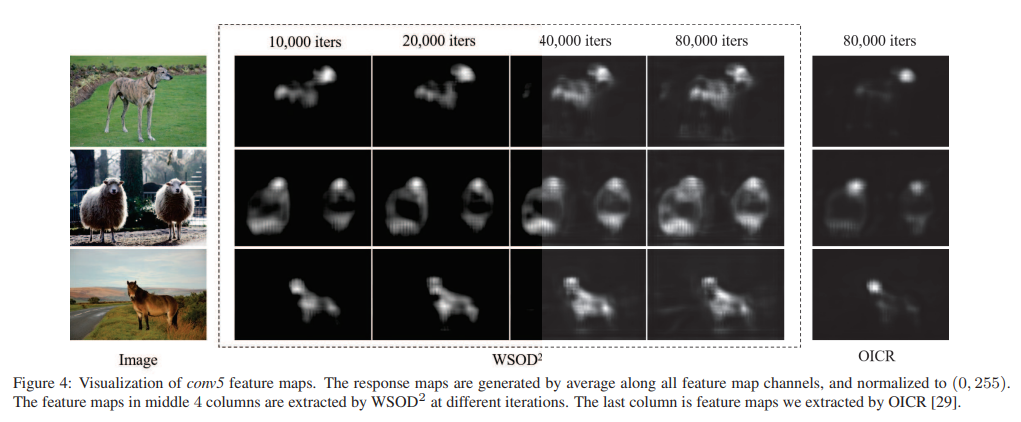
WSOD2는 OICR 대비 전체적인 객체의 위치를 잘 찾는 것을 확인할 수 있음.
WSOD2 can gradually transfer the response area from discriminate parts to complete objects.
마지막으로, 해결해야 할 문제를 하나 소개함.

“Person” class의 경우, 대부분의 WSOD 아키텍처가 사람의 얼굴만을 탐지하는 문제가 있음. 이는 현재 데이터셋의 person class가 다른 부분(팔, 몸통 등)은 누락되어도 human face만은 포함하기 때문에 발생한 문제로 보임.
이러한 문제를 해결하기 위해, human structure prior 등을 사용할 수 있음.
