Introduction

Limitation of MLP

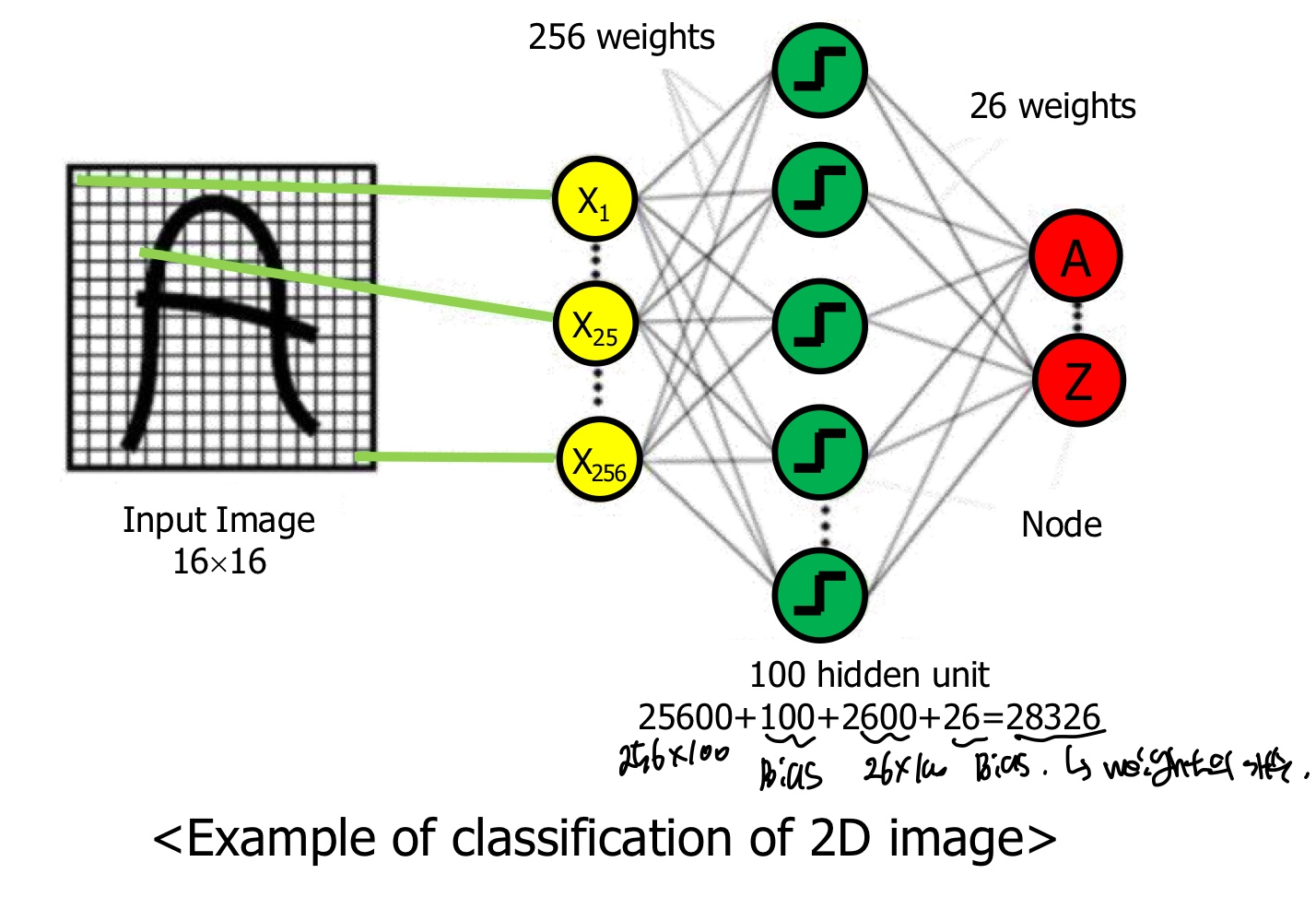
gray-scale인 2D image를 classification하기에는 너무 많은 parameter의 개수가 필요하다. 위의 예시를 든 MLP에서 단순히 2layer인 것에 불구하고 무려 28,326개의 parameter가 필요하다.

Intro CNN

CNN의 가장 흔한 pipeline은 다음과 같다.
1. 2D Image Input
2. Feature Extraction
3. Shift & distortion invariance
4. Classification
5. Output

Feature Extraction에서는 Image에 Convolution연산을 적용하여 feature를 추출한다. 이때 convolution연산을 하기 위해서는 filter가 필요한데 filter의 element는 parameter로 학습하면서 update된다.

Shift & distortion invariance는 아무리 data가 이동과 공간에 대한 왜곡이 있더라도 CNN을 통해 feature를 계층적으로 추출하고 이러한 과정에서 불변성을 달성하게 된다.

Classification은 Feature Extraction에 대한 정보를 MLP에서 학습하여 output을 출력하게 된다. 이때의 output은 classification이기 때문에 확률이 각 class별로 확률값이 나오게 된다.

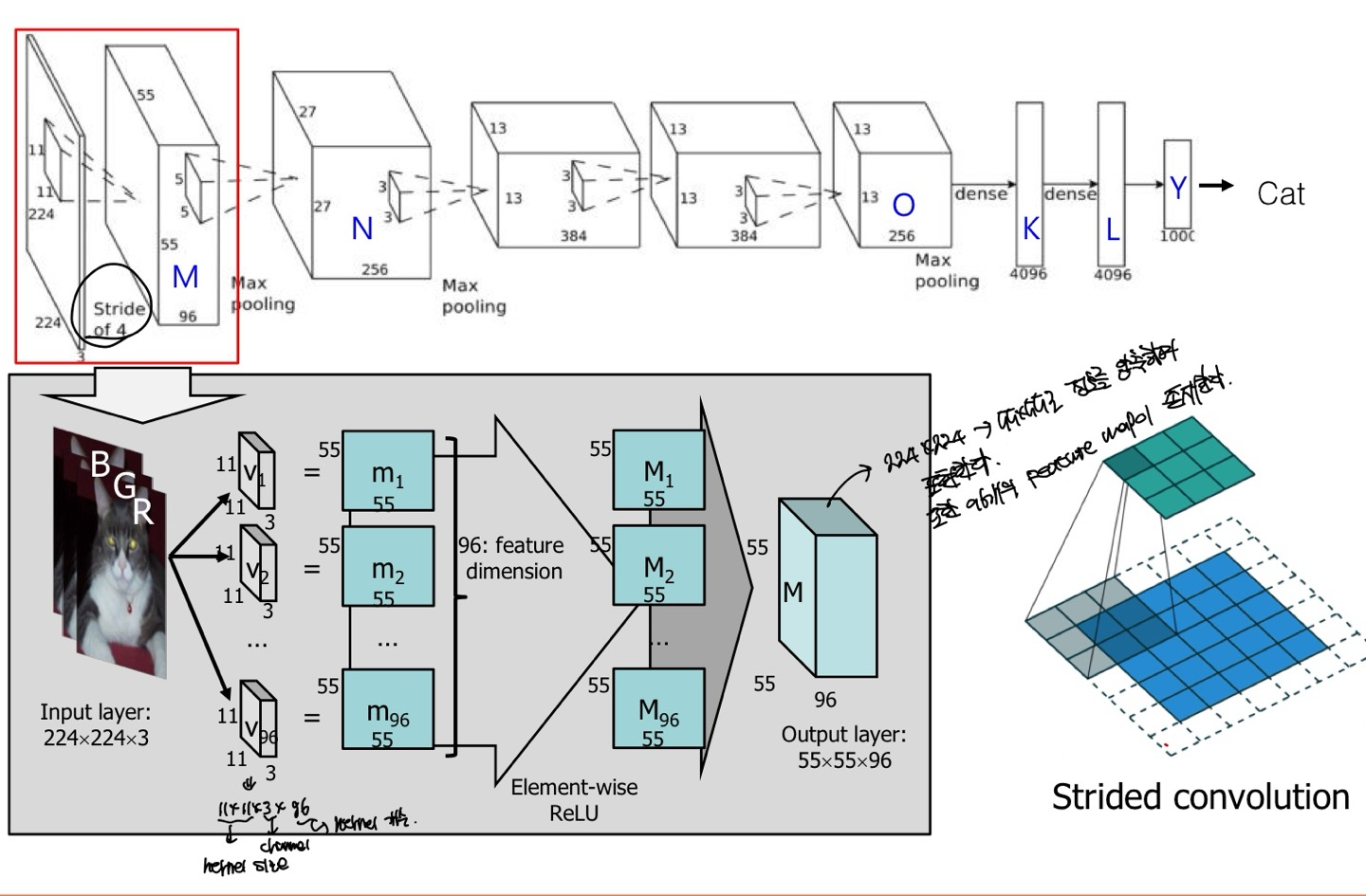
CNN의 대표적인 모델인 AlexNet의 첫번째 conv layer로 설명해보자면, 일단 Input Image로 224x224x3으로 224x224크기의 RGB Image가 들어온 것이다.
이것을 stride가 4이고, kernel size가 11x11인데 이것을 적용하면 output으로 55x55x96이 나온다고 한다.

padding의 유/무는 잘 모르겠지만 stride가 4이고 kernel size가 11x11이면 Image의 크기가 줄어든다는 것은 짐작할 것이다. 하지만, output의 channel이 96은 이해가 안될수 있는데, 이것은 filter의 개수가 96개이기 때문에 output의 channel이 96개가 되는 것이다.

더 자세히 말하자면, 먼저 filter의 channel은 항상 input image의 channel과 같아야한다. 그래야 convolution 연산이 가능하다. 따라서 filter의 channel은 input image에 종속적이며 filter의 개수는 hyperparameter로 사용자가 직접 적용할 수 있다. filter의 개수는 output의 channel의 크기인 것을 잊지 말도록 하자.

Spatial Pooling (sub-Sampling)

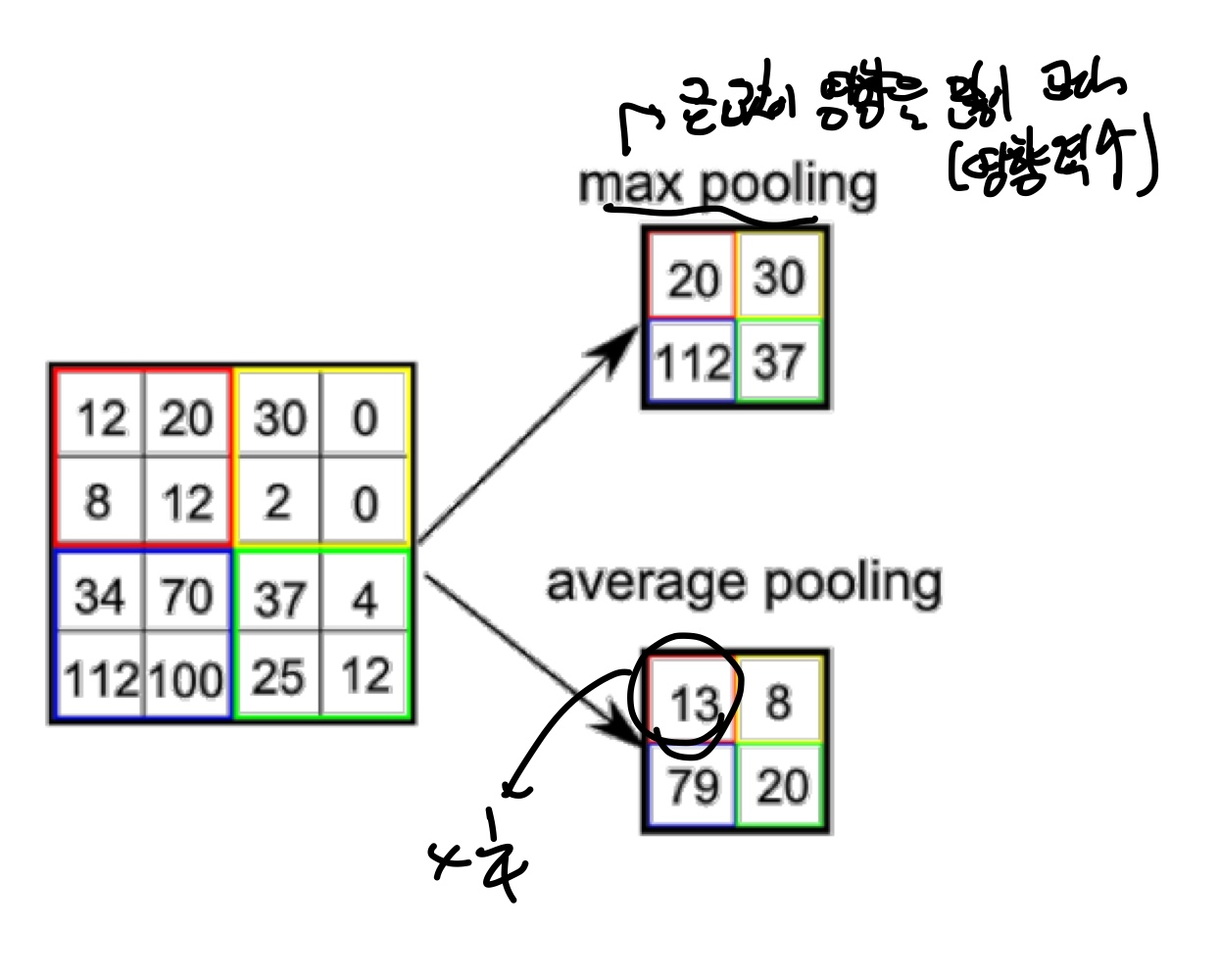
Spatial Pooling은 sub-sampling이라고도 불리우며 다음과 같은 특징을 가진다.

• 대표적으로 Max-pooling과 Average-pooling이 있다.

• 대표적인 효과로 classification하는ㄷ scale과 position에 invariance하다는 것이다.

• Image data를 작은 size의 image로 줄이는 과정으로 pooling을 하는 이유는 output feature map의 모든 data가 필요하지 않기 때문에 Inference 하는데 있어, 적당량의 data만 있어도 된다.

• parameter(weight)의 수가 줄어들어, overfitting을 억제한다.

• memory를 절약할 수 있다.

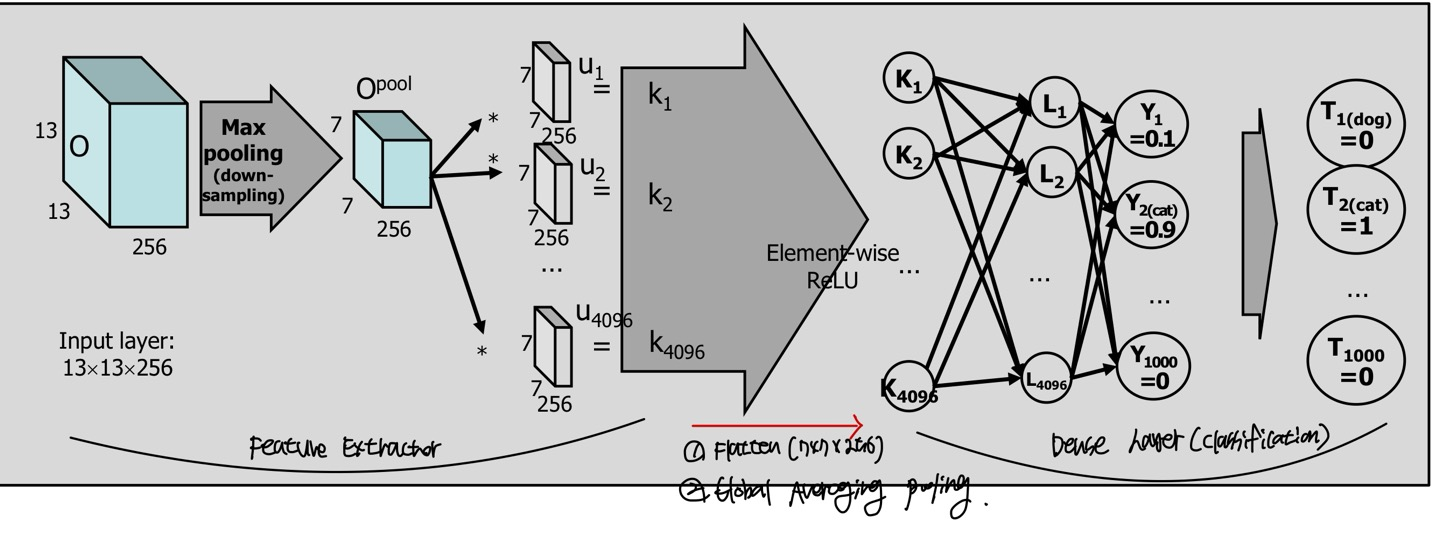
Featuer Extractor에서 Dense Layer(Classification)으로 넘어갈때를 그래프로 나타낸 것이다.
넘어갈때 MLP는 1D를 input으로 받기 때문에 feature에 대한 정보를 1D로 고쳐야하는데 이때의 방법은 Flatten과 GlobalAveraging pooling이 존재한다.

Flatten은 단순히 filter를 적용한 output의 filter를 1D로 고치는데, 예를 들어 7x7x256이 있다고 한다면 1D로 고치기 위해 7x7x256을 vectorization을 한다.

GlobalAveraging pooling(GAP)은 같은 channel의 feature들을 모두 평균을 내고 channel의 개수만큼 element 개수를 가지게 된다. GAP은 FC layer를 없애기 위해 만들어졌으며 FC layer는 마지막 feature와 matrix곱을 하여 feature전체를 연산에 대상으로 삼아서 결과를 출력하기 때문에, image전체를 보고 출력을 만들어내는 것과 같다. 이에 따른 결과로 위치에 대한 정보가 없어지기 마련이다.
또한 FC는 input image의 size가 정해져있고, GAP은 정해져 있지 않으며 GAP을 output layer에도 쓸 수 있다.

위 그림에서는 GAP이 아닌 Flatten을 적용한 예시이다.

---

BackPropagation of CNN

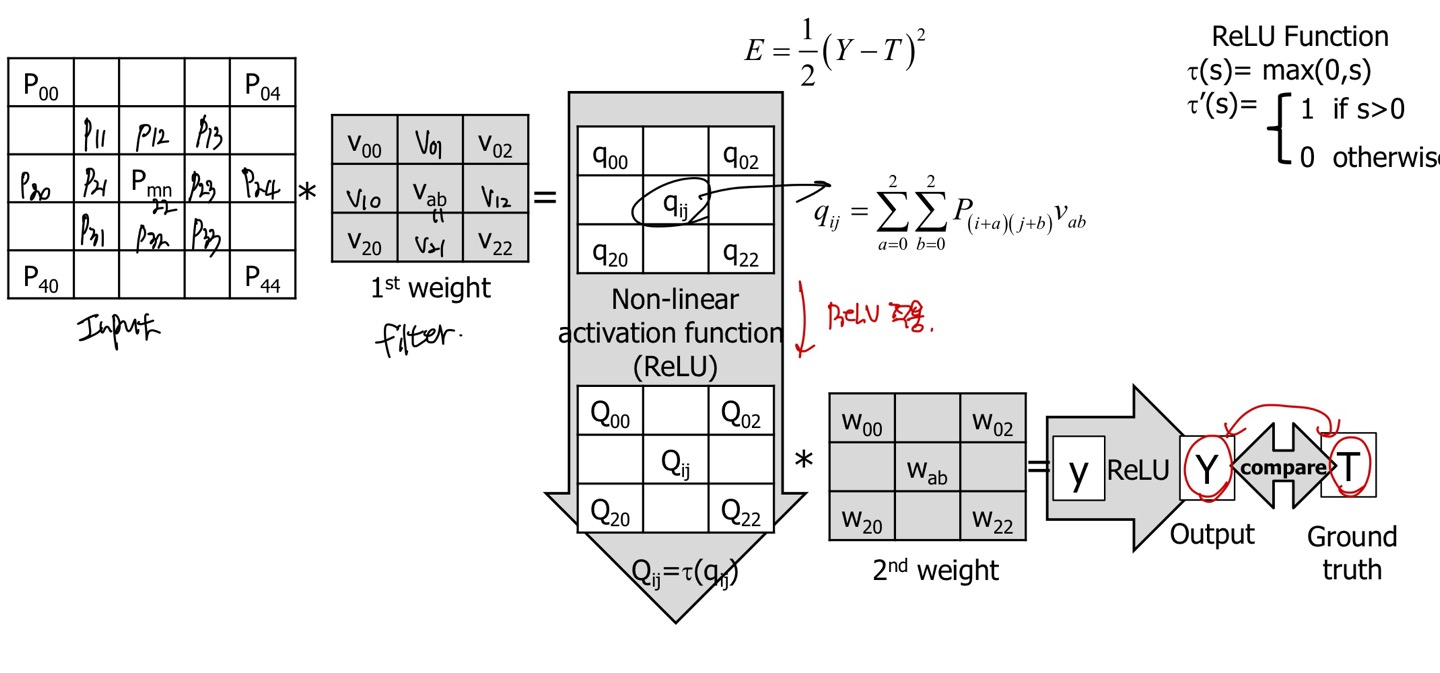
위 그림은 수식과 내용이 복잡해보이지만, 우리가 알고 있는 backward를 MLP가 아닌 CNN에서 적용하는 것이기 때문에 별로 어렵지 않다.

1 channel과 stride, pooling, padding이 없다고 가정하고 설명하겠습니다.

처음 Input Image를 넣고 filter를 적용할때 output의 특정 $q_{ij}$를 얻기 위해서 위의 시그마 수식을 넣으면 되는데, 단순한 convolution연산을 나타낸 것이다.

conv 연산을 하고 ReLU를 적용한 것이 τ($q_{ij}$)이며, 이것을 $Q_{ij}$라고 치환했다고 한다.
이것을 또 conv연산을 한 것이 y이고 ReLU를 적용한 output값이 Y(대문자 y)이다.

우리는 predict값과 real값의 차이를 줄이기 위해서 backward pass를 진행한다. 이때 predict값은 Y이고, ground-truth값은 T이다.

이제 backward pass를 해보자.

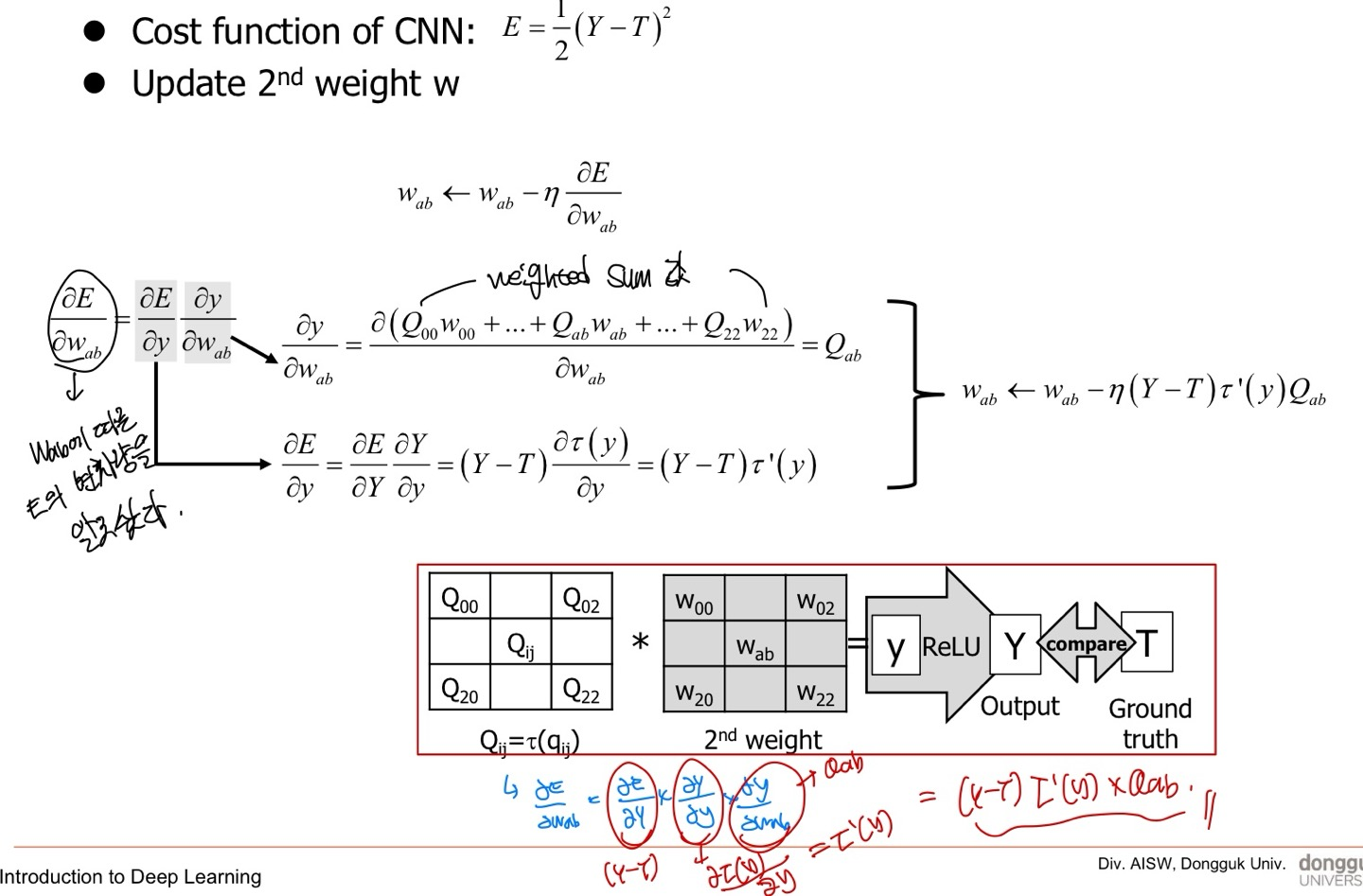
먼저 Loss function에 대한 정의와 $E / w_{ab}$를 알고 싶다고 한다.
즉, 손실함수 $w_{ab}$에 따른 E의 변화량을 알고 싶다는 뜻이다.

식을 보게 되면 단순히 ∂E/∂y x ∂y/∂$w_{ab}$ 로 나누어서 계산하는 것을 보여준다.

$w_{ab}$값을 update하기 위해서는 gradient descent를 이용해야하며 위의 그림에서 식을 나타내고 있다.
내가 여기서 놓친 점은 y에서 ReLU를 적용한 Y가 τ(y)로 표시되었다는 것 이다.
내가 파란색으로 쓴 식을 보면 더 이해가 잘 될 것이다.

하지만 2번째 weight만 구해서는 재미가 없다.
나는 손실함수 E가 $v_{11}$에 따른 변화량을 보고 싶다.

수식은 다음과 같다.

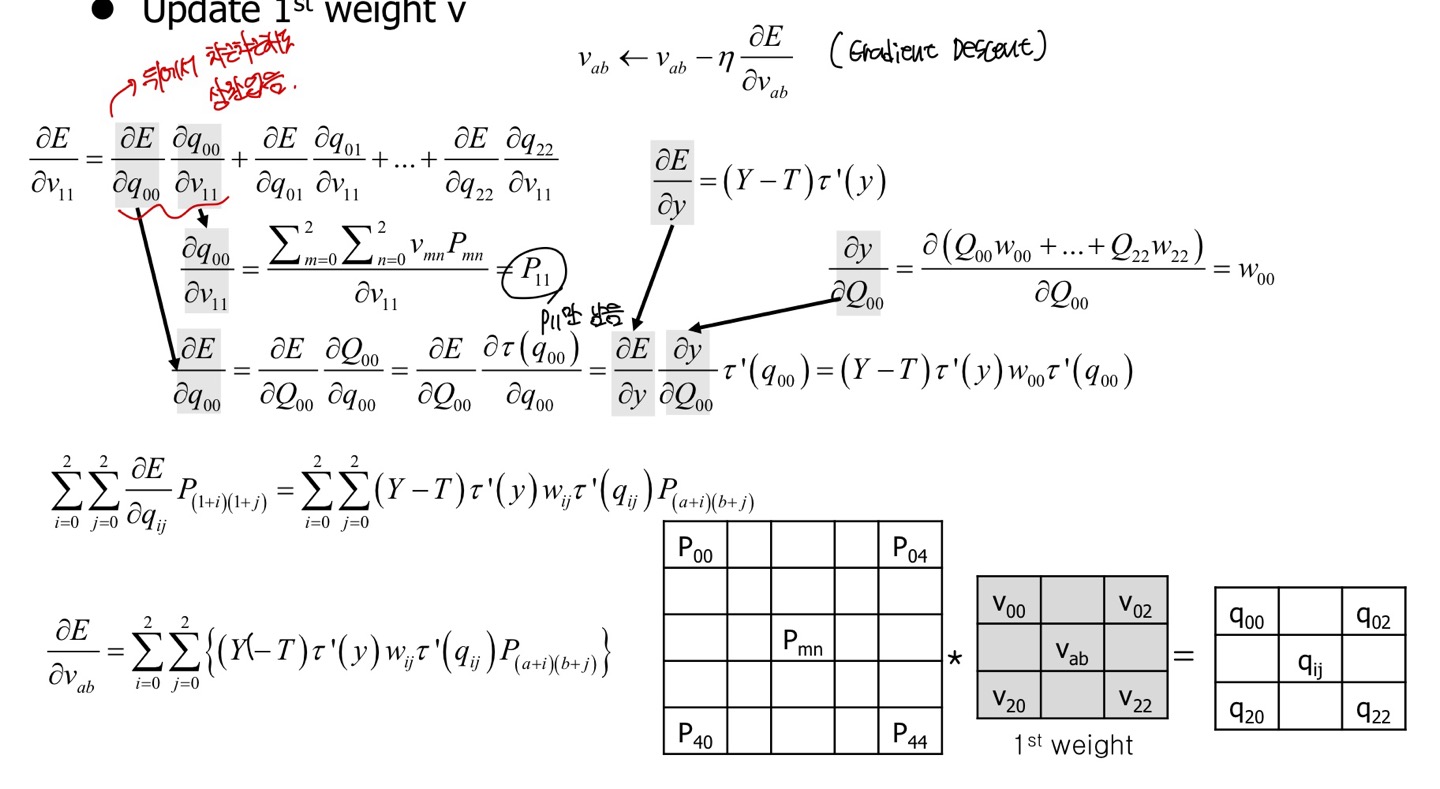
솔직히 나는 ∂E / ∂$q_{00}$ x ∂$q_{00}$ / ∂$v_{11}$ ~ 에서부터 시작하는지 잘은 모르겠지만, 나는 뒤에서부터 차근차근 했다.

내가 backward pass를 적용한 식은 다음과 같다. 결과는 위와 당연히 같다.

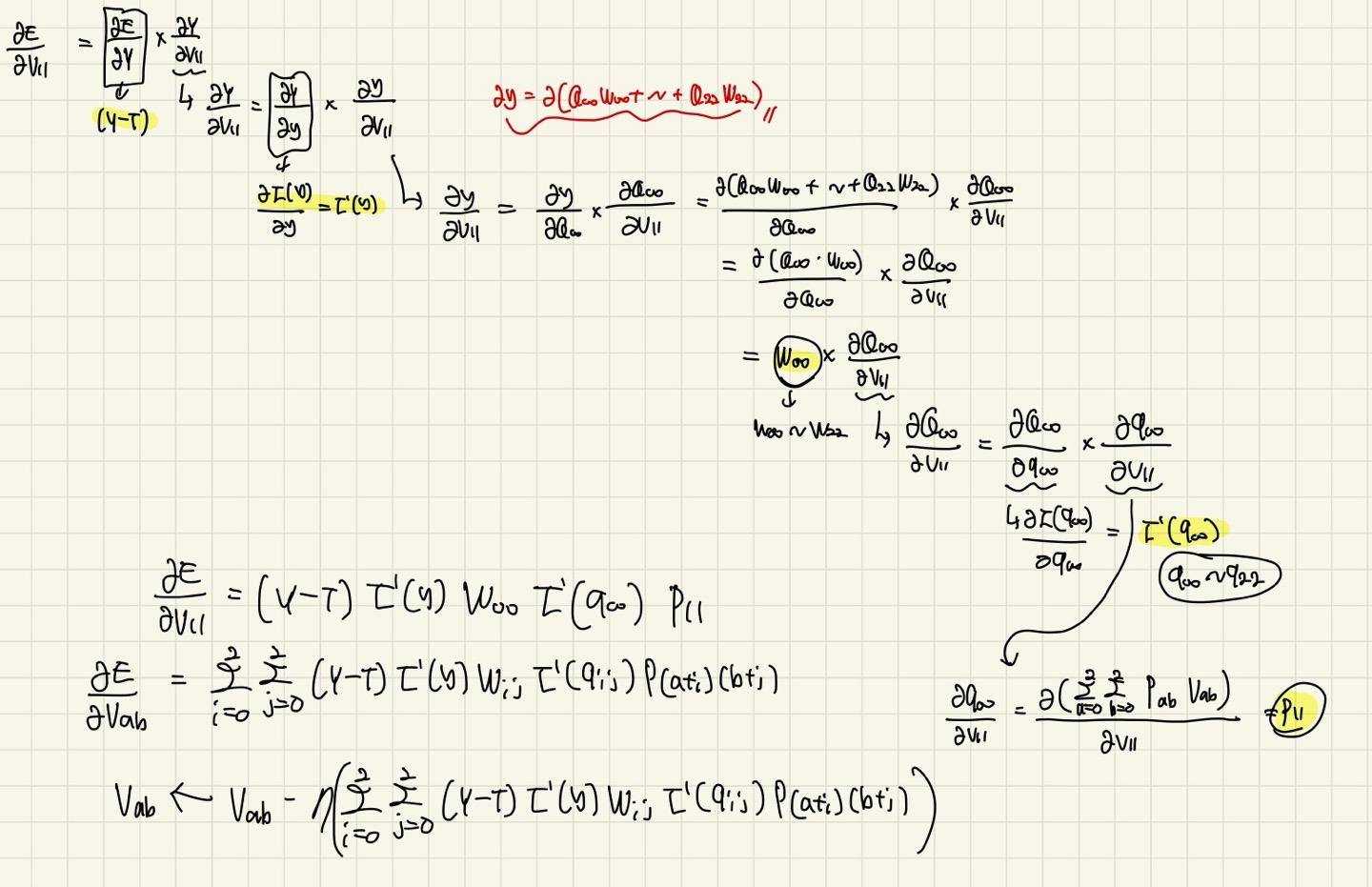
convolution의 연산이 있기 때문에 모든 element에 대해서 ∑가 필요하다.
먼저 처음에 나타낸 수식을 차근차근 따라가다보면 내가 쓴 식을 제대로 이해할 수 있을 것이다.
마지막 gradient descent를 통해 $v_{11}$에 국한하지않고 일반화한 식을 나타냈다.

---

Image Classification

Confusion Matrix

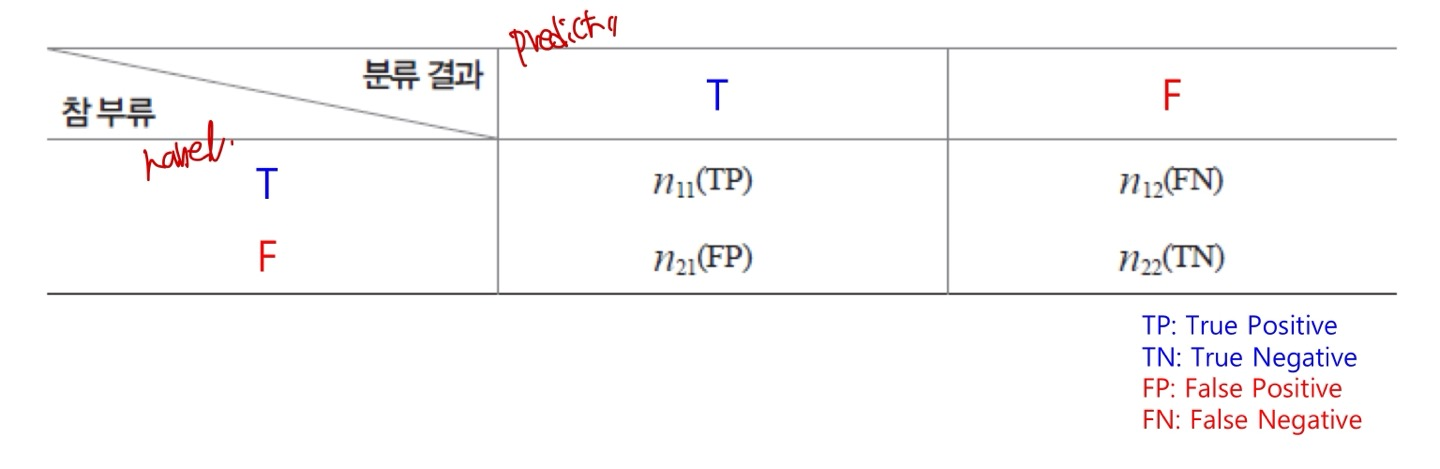
먼저 Image Classification은 딥러닝 모델이 실제로 Image를 분류하는 작업을 말한다. 예를들어, 강아지와 고양이를 구별해야하는 binary classification이 대표적인 예시이다.

위의 confusion matrix는 강아지와 고양이를 잘 구별했는지에 따른 성능지표를 나타낸다. 물론 정확도(Accuracy)만으로 모델의 성능을 판별할 수도 있겠지만, overfitting의 문제점 등과 관련해 정확히 알기 어려워 다양한 성능지표 중 1개라고 보면 된다.

먼저 Precision(정밀도)는 TP / (TP+FP)이며, 모델이 긍정(정답)이라고 판단(Predict)한 것 중에서 실제로 긍정(정답)인(label) 비율을 뜻한다.

Recall(재현율)은 TP / (TP+FN)이며, 실제로 긍정(정답,label)인 것 중에서 모델이 정확하게 식별한 긍정(정답,predict)의 비율이다.

$F_B$은 f-1 score의 일반화 된 형태이며, 식은 {(1+$B^2$) x (precision x recall)} / ($B^2$ x precision + Recall) 이다.
B값에 따라 precision과 recall의 상대적인 중요성을 조절할 수 있으며, B > 1이면, precision이 recall보다 중요, B = 1이면 동일한 중요성, B < 1이면, recall이 precision보다 중요하다는 뜻이다.

ResNet

Residual Learning

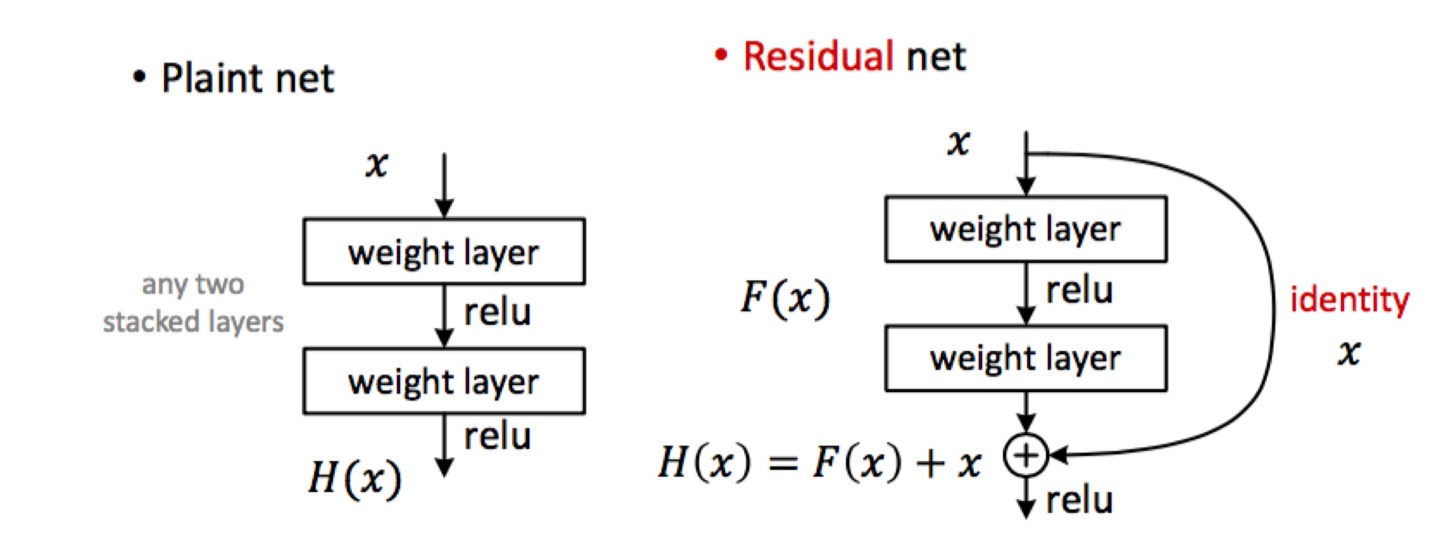
ResNet의 핵심인 Residual Learning에 대해서 알아보자.
먼저 해석해보면 차이만을 이용해서 학습한다고 한다. 이 학습은 backwardpass를 할 때의 학습을 의미하는 것이다.

더 자세히 살펴보자.

오른쪽 Residual net의 2 stack layer를 봐보자, 편하게 layer라고 부르겠다. 이 layer는 단순히 output F(x)를 똑같은(identity)값 X를 더해서 ReLU를 통과시키자는 것이다.
식에서 H(x)는 Layer에 들어온 X를 받아서 만들고 싶은 이상적인 output이고, 이 H(x)를 F(x) or X+F(x) 중에서 후자가 더 좋다는 결론이 나왔다는 것이다.

이러한 결론을 알기 위해 다음과 같은 가정을 하겠다.
H(x)가 x와 비슷하다.
이때 skip-connection이 없는 MLP라면, 가중치 초기화는 x가 되어야한다.
만약 skip-connection이 있는 MLP라면, 가중치 초기화는 0, 즉 영행렬이 되어야한다.
하지만 가중치는 0근처로 초기화가 된다는 것을 우리는 잘 알고 있다. 그렇다면, 가중치를 0 근처로 학습하고 LOSS를 줄일 수 있다면 얼마나 좋을까? (0근처로 학습하면 H(x)와 x가 비슷한 값을 가지게 되는 것)

앞에서 가정한 이유는 다음과 같다. 만약 layer가 엄청 깊다고 한다면, layer마다의 output값은 조금씩 바꿔 나가는 것이 이상적이다. 왜냐하면 layer마다 variance가 매우 심하면 overfitting이 일어난다. 즉, 모델의 generalization이 매우 어려워진다.
그래서 우리는 layer마다 output값을 조금씩 바꿔나가는 것이 매우 이상적이면 variance값이 크지 않다는 것을 의미하고 이는 overfitting을 억제하는 효과도 일어나게 된다. 그래서 우리는 "H(x)와 x가 비슷하다"라고 가정한 것이다.(이는 왼쪽 Plaint net을 기준으로 설명한 것)

우리는 skip-connection이 있다면 H(x)는 x와 비슷한 값을 얻기가 쉬울 것이며, 이는 모델에게 H(x)와 x가 비슷할테니 layer 1개에서 모든 것을 다 바꾸려하지말고 조금씩만 바꿔 나가라 라고, 모델에게 알려주는 것이다.
그래서 내릴 수 있는 결론은 layer마다 값을 조금만 빠구는 것이 좋은 Network가 되는 것이다.

논문에서는 실제로 skip-connection이 없는 것은 layer의 output마다 variance가 있는 것보다 크다는 것을 증명했다고 한다.

정리하자면, 기존 Plaint net이 x가 H(x) 방향으로 학습하였다면, Residual net은 x가 F(x) + x로 이상적인 값으로 학습하는 것이다. 이는 단순히 H(x) = F(x) + x 이므로, F(x) = H(x) - x가 되는데 F(x)를 학습시키는 것이 되어버리므로 이를 "Residual learning"이라고 부르게 되었다.

Architecture

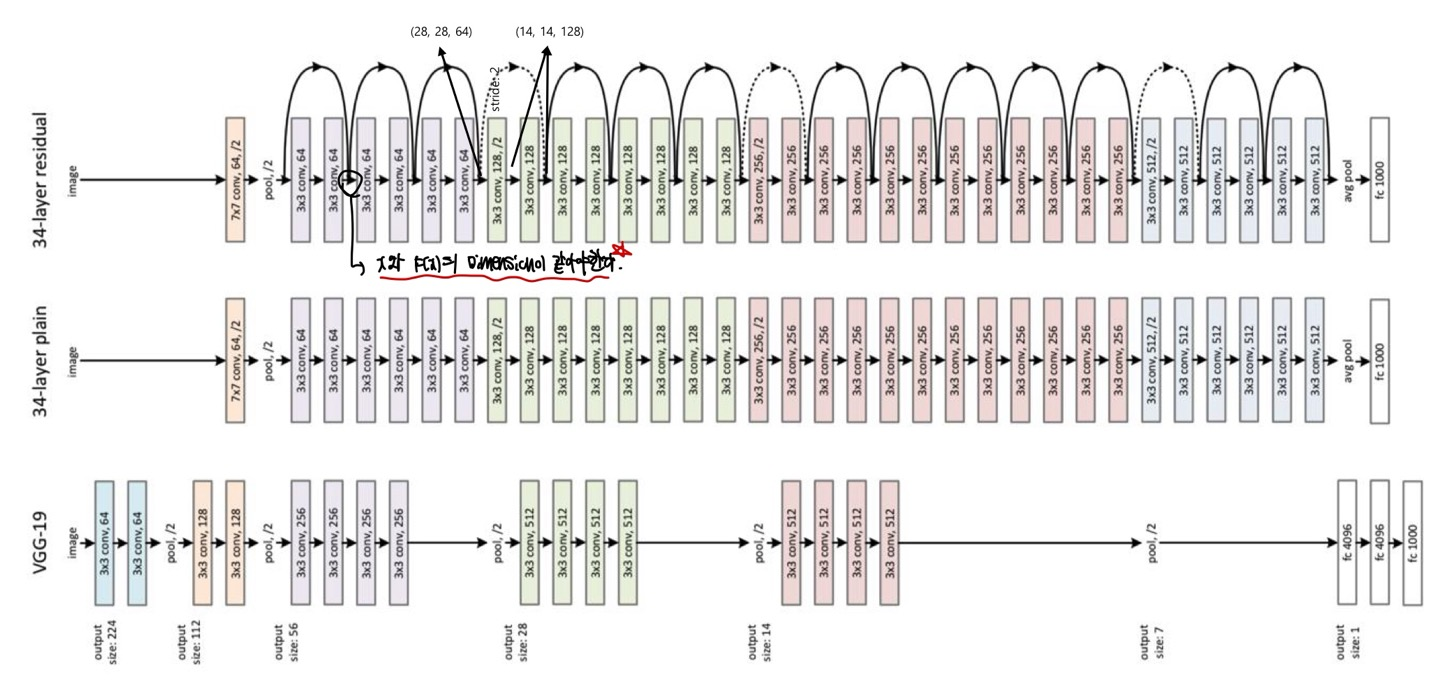
ResNet의 구조인데, residual learning이 있는 것과 없는 것이 있고, VGG-19와 비교할때 Resnet이 layer가 skip-connection을 통해 layer가 더 깊다는 것을 한 눈에 알 수 있다.

34-layer residual에서 주의할 점은 당연히 x와 F(x)의 dimension이 같아야함에 잊지말고, 실선은 identity mapping, 점선은 downsampling으로 Resnet은 stride를 2로 설정하여 downsampling을 한다고 한다.

BackPropagation

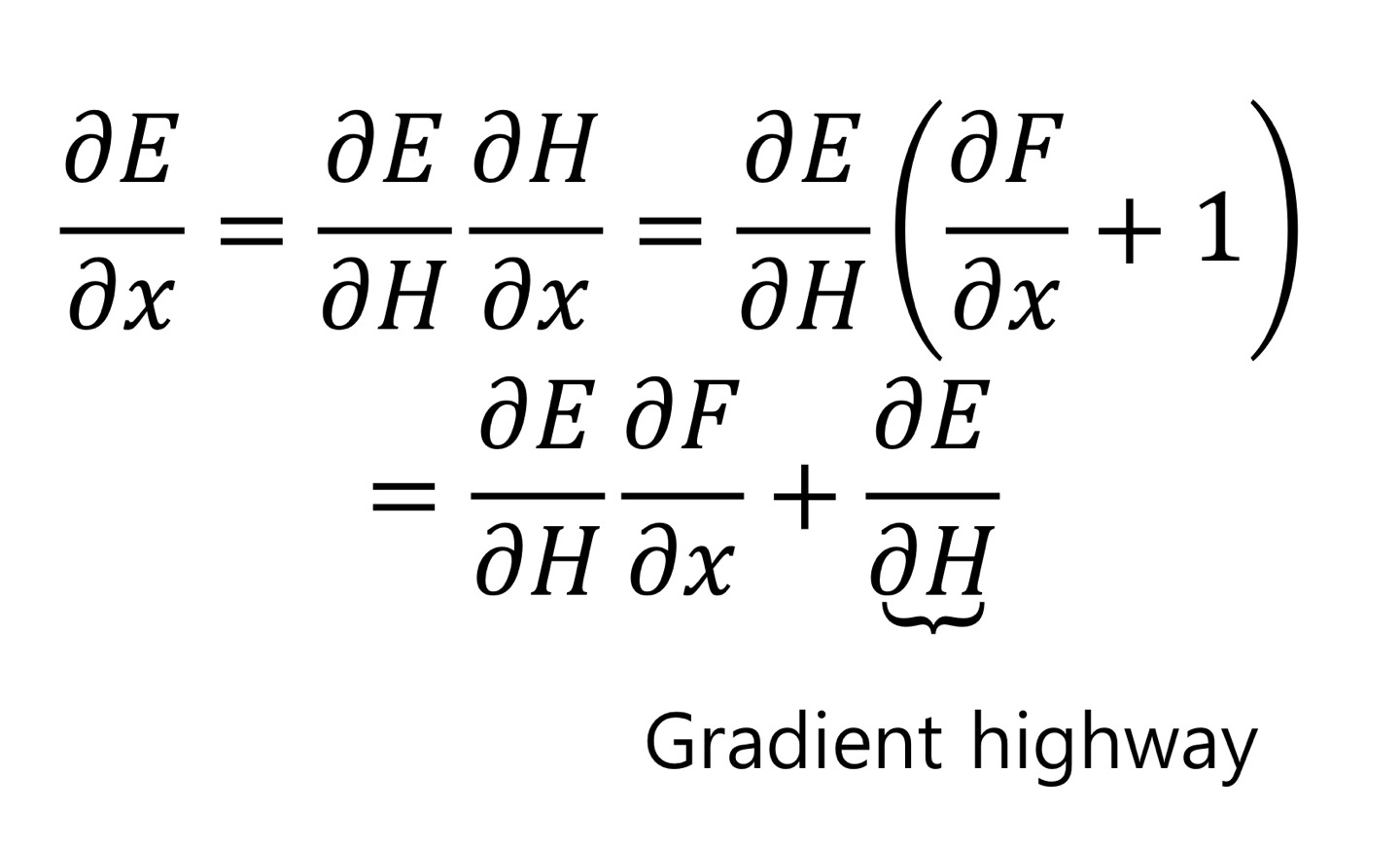
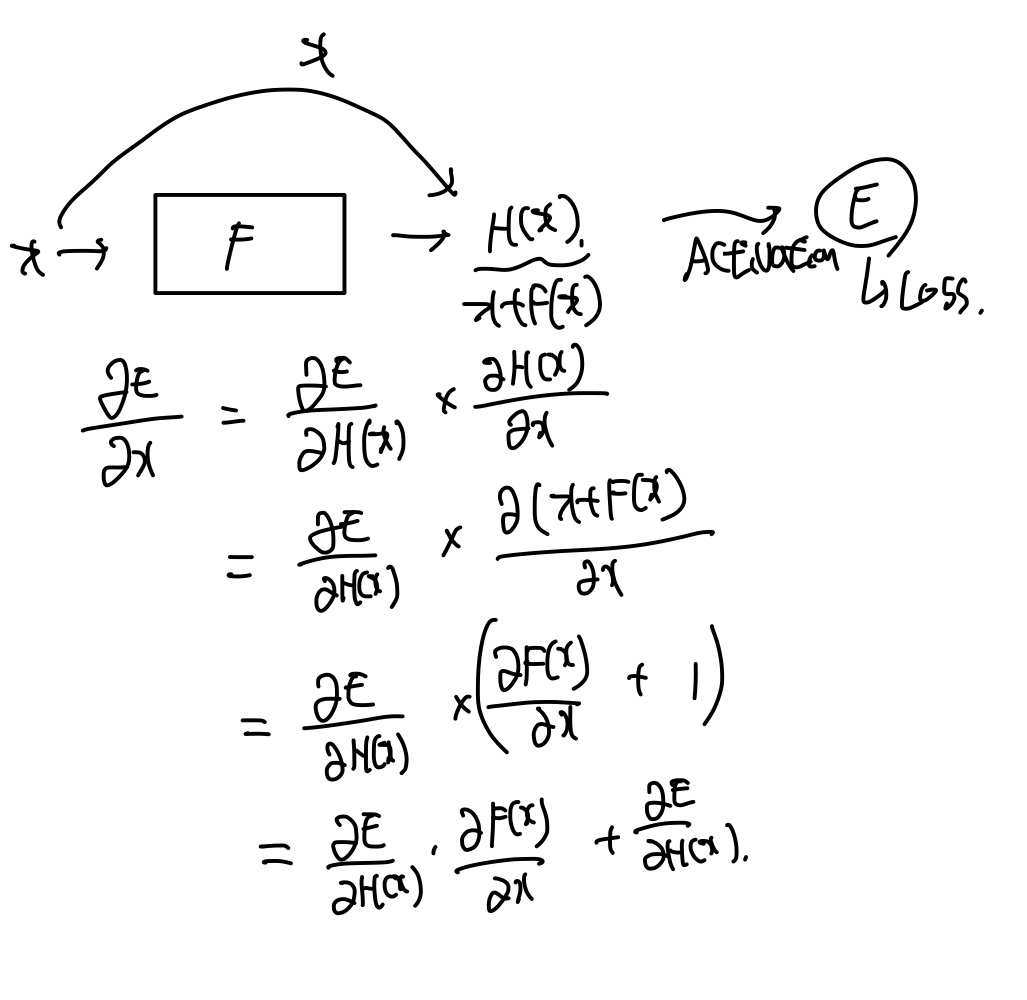
위의 식이 이해가 되지 않을 것 같아, 도식화 해보았다.
이 skip-connection에 있는 layer를 backward하게 되면 1의 값이 남게 되는데 이는 gradient vanishing 현상을 막아준다. 이는 gradient highway로 인한 현상인데 이도 이해가 잘 되지 않을 것 같아 직접 예시를 만들어보았다.

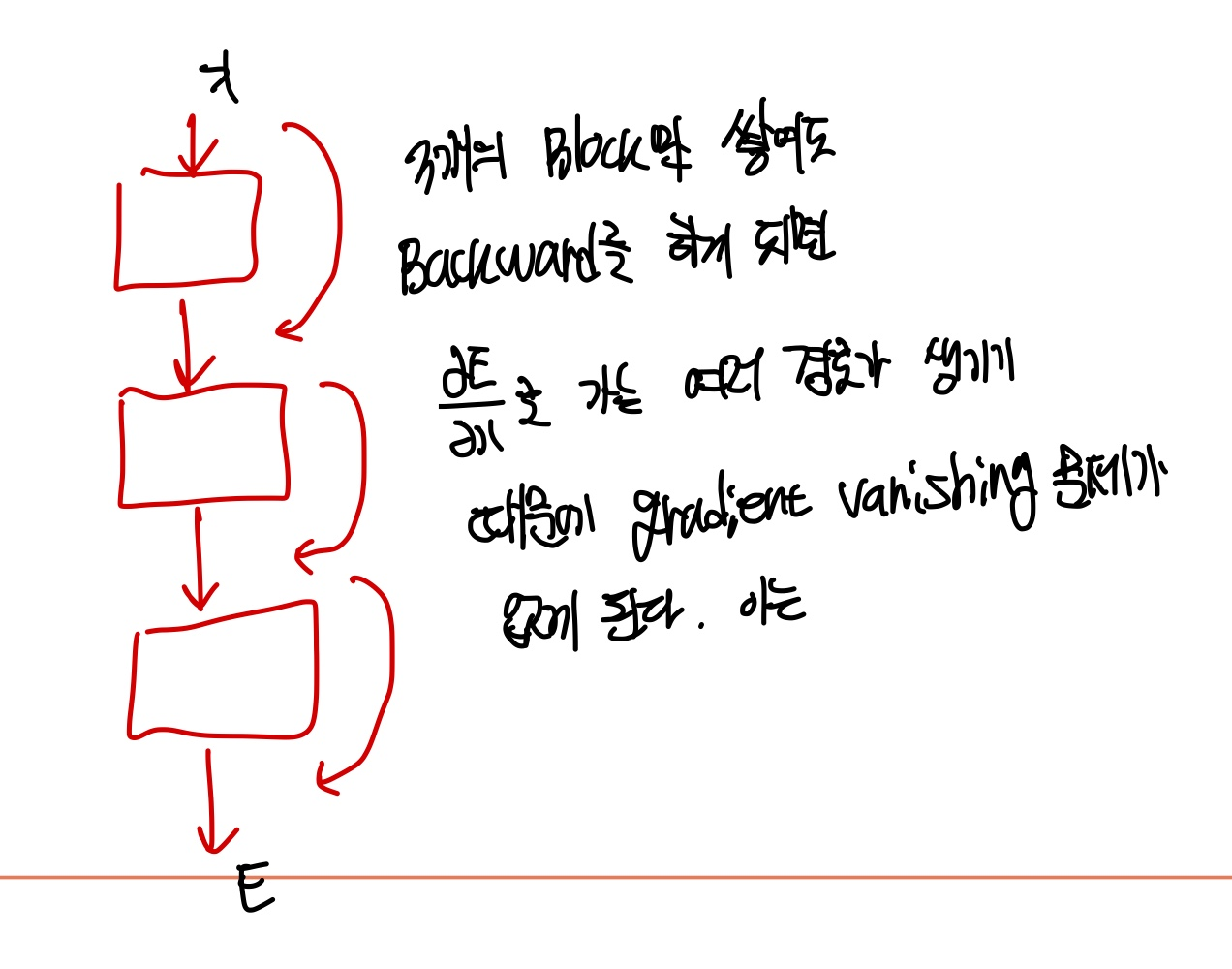
위에서 단순히 3개의 layer 즉, 3개의 block만 쌓게 되어도 backward를 하게 되면 ∂E / ∂x로 가는 여러 경로가 생기게 된다. 여기서 ∂E / ∂x로 가는 경로만 해도 8개가 되기 때문에 gradient가 vanishing이 되지 않도록 1의 값을 ∂E / ∂x에 8번 더해주는 셈이다.

EfficientNet

Compound Scaling

우리는 모델의 성능이 좋아지기 위해서 layer를 더 깊게한다든지, feature map를 더 늘린다든지, Input data의 resolution을 더 늘리는 방법으로 모델의 성능이 좋아질 수 있었다.

위 3가지의 방법으로 EfficientNet은 3가지의 scaling factor를 동시에 고려하는 compound scaling기법을 제안했다.

layer의 depth를 늘리는 방법은 가장 흔한 scale-up방법으로 깊은 모델은 더 높은 성능을 내는 것은 이미 잘 알려진 사실이다. 그러나 layer를 계속 깊게 쌓는 것은 한계가 존재하기 마련이다. 이에 따른 증명은 ResNet-1000과 ResNet-101과 거의 비슷한 성능을 내는 것을 확인할 수 있었다.

feature의 width를 넓게 할수록 우리는 미세한 정보, 즉 fine-grained feature들을 더 많이 담을 수 있다.

필자도 Input data의 더 큰 image를 넣을수록 성능이 올라간다는 것을 처음 알게 되었지만, 실제로 input image의 크기가 224x224인 모델보다 331x331 이미지를 사용했을 때 더 좋은 성능을 낸다는 것을 증명했다.
실제로 object-detection영역에서는 600x600을 사용하면 더 좋은 성능을 보임을 확인했다.

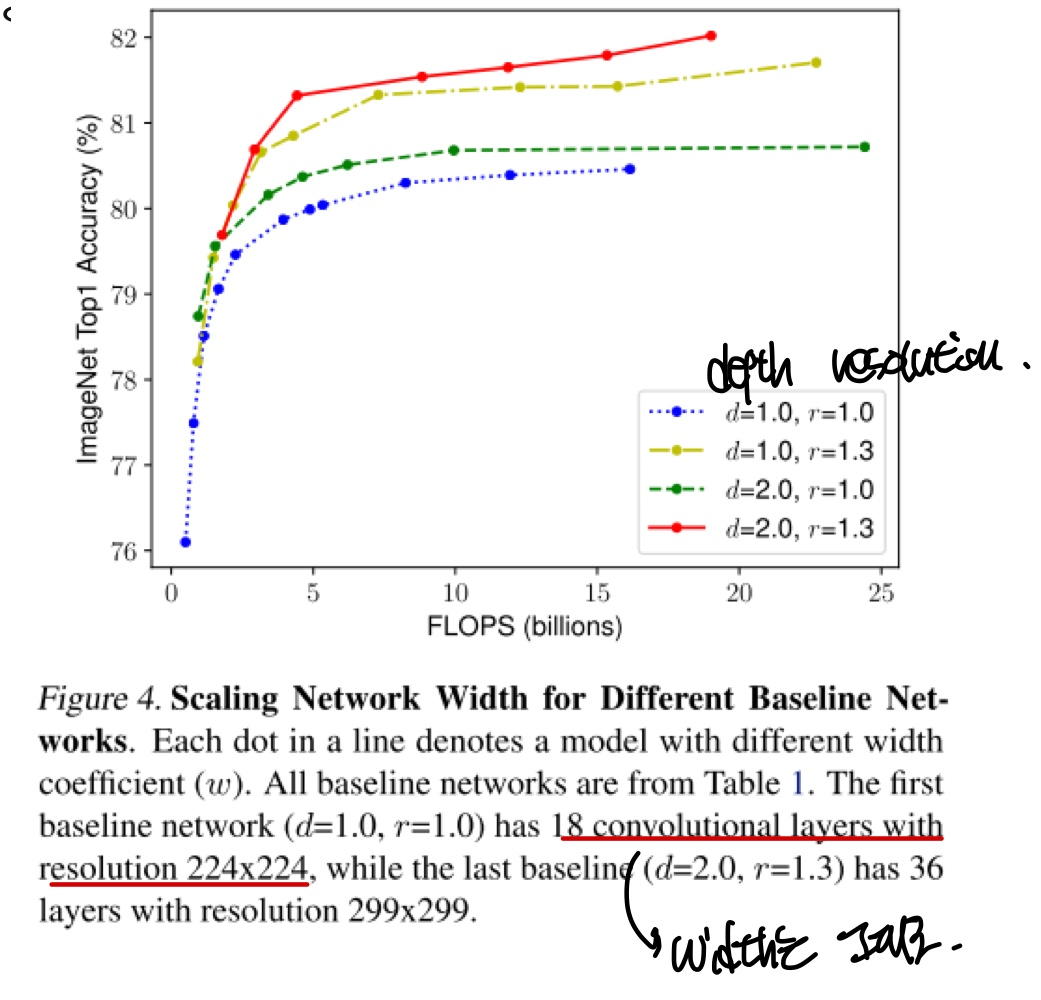
blue line과 yellow line을 비교해보았을때, resolution을 증가해주니 실제로 accuracy가 높아지는 것을 볼 수 있다. 하지만 layer의 depth와 resolution, feature의 width를 동시에 증가시켜준 것이 red line에서 보여졌고 각각의 값에 따른 지수값은 gridsearch를 통해 최적의 값을 도출한다고 한다.

Architecture

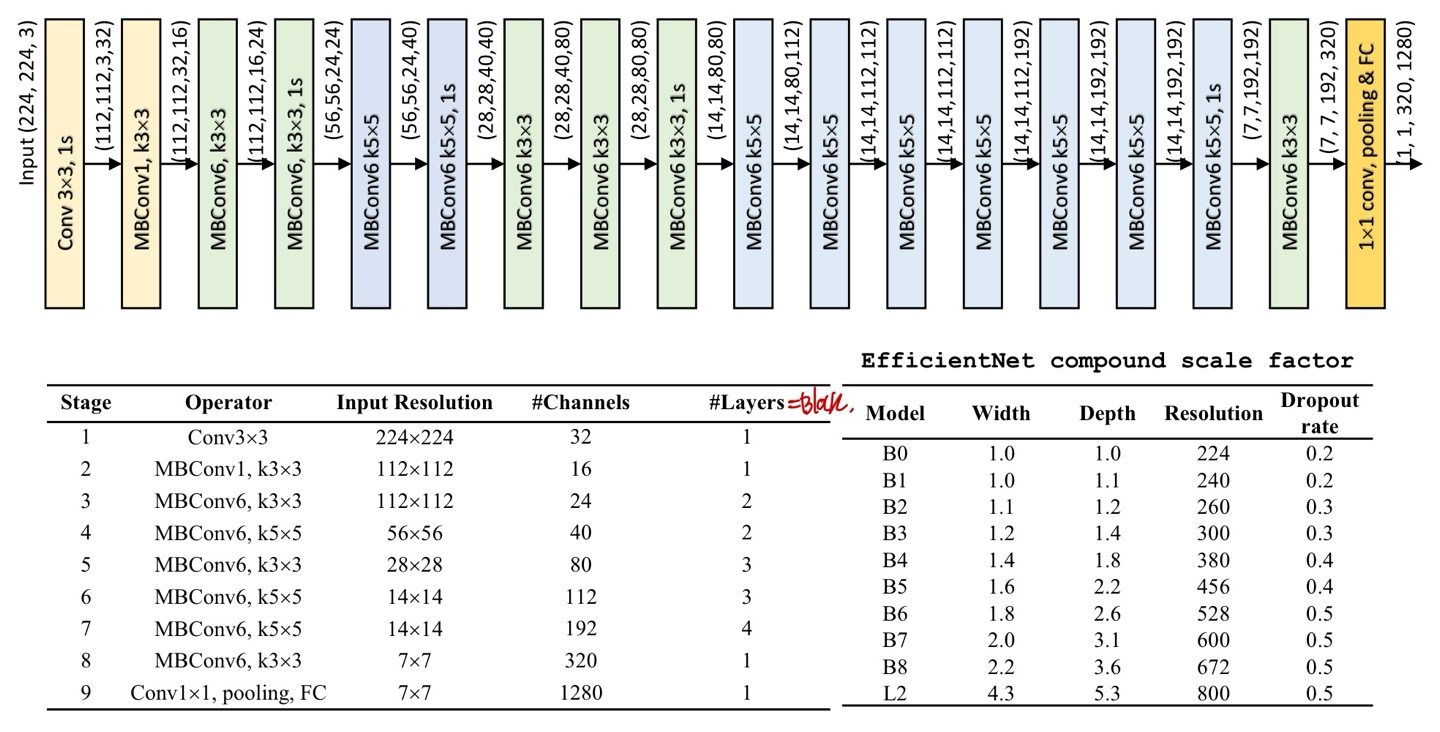
구조는 위와 같은데, 여기서 MBConv(숫자)가 걸린다.

MBConv는 Mobile inverted bottleneck convolution으로 Depthwise Separable Convolution과 pointwise convolution의 개념을 알아야한다.

Depthwise Separable Convolution은 feature map에서 각 feature별로 쪼개서 conv연산을 적용하는 것이다. 일반적인 conv연산은 모든 feature map에 conv연산을 하였다면, 이는 feature map별로 conv연산을 해주는 것이다. 이를 통해 우리는 parameter수를 줄일 수 있다고 한다.

Pointwise convolution은 kernel의 크기가 1로 고정되어 있는 1D Convolution으로 여러 개의 channel을 1개의 새로운 channel로 합치는 역할을 한다.

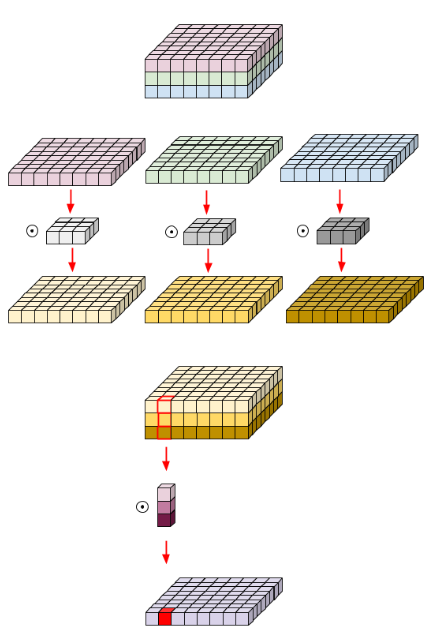
위의 설명을 도식화하면 위와 같다.

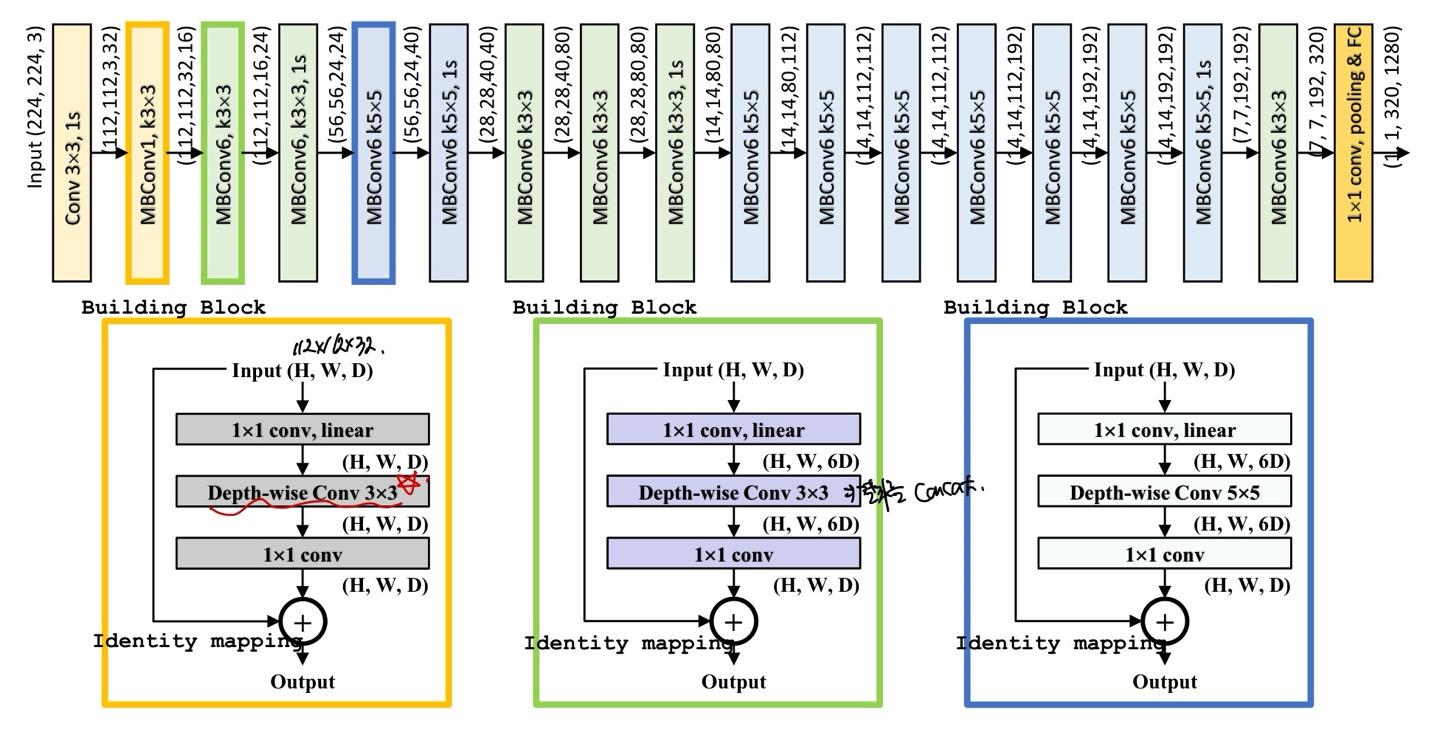
위에서 단순히 MBConv1과 MBConv6로 나타내져 있는 부분을 설명하겠다.

노란색으로 박스쳐져 있는 MBConv1을 보게되면 1x1 convolution의 output channel이 D로 input의 channel과 똑같다. 그래서 MBConv1인 것이다.

그러나 초록색과 파란색을 보면 1x1 convolution에서는 input과 1x1 conv의 output channel이 다르다. 이는 1x1 conv연산을 통해 output channel수를 조절할 수 있음에 가능한 것이다.
또 다시 1x1을 통해 input과 최종 output channel의 수를 똑같이 만들어줌으로써 concat이 가능하게 된다.
이를 통해 우리는 6배 더 높은 차원으로 mapping하고 그 다음 다시 1/6으로 줄여줌으로써 더 다양한 feature를 학습할 수 있게 해준다.

SENet

SENet이 나온 이유는 Input data를 conv연산을 하게 되면 각 channel들은 서로 맥락적인 정보를 알 수 없다는 것에서부터 시작된다.

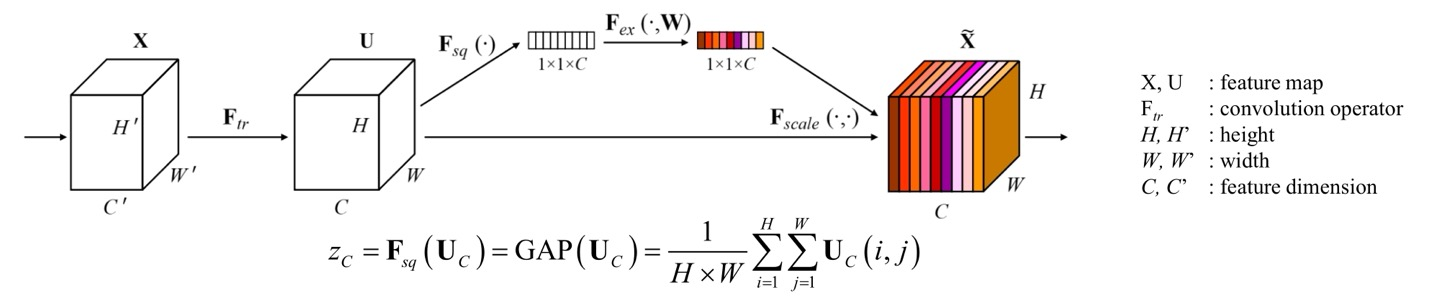
위의 구조를 보면, Input data X에서 U로 conv연산을 때리는 $F_{tr}$함수의 filter들은 각자 목표하는바가 다르다는 것이다. 목표하는바가 다르니, 정보 활용이 매우 제한적이게 되므로 SENet은 이러한 feature들을 non-mutually exclusive하게 사용한다는 것이다.

그러면 핵심을 알았으니 어떻게 가능한지 살펴봐야할 것이다.

위의 수식이 해석하기 어려우면 말로 해주겠다.
먼저 $Z_c$는 GAP(Global Averaging Pooling)을 각 channel마다 적용해준 값이고 vectorization이 된 값이다. 이것을 초기화된 가중치 $w_1$과 함께 Fully connected layer를 만들고 그 결과들을 ReLU에 넣게 된다.

ReLU에 넣은 결과를 다시 초기화된 가중치 $w_2$와 함께 FC를 만들고 그 결과를 다시 sigmoid함수로 넣어주게 된다.

필자도 밑의 $F_{scale}(U_c, S_c) = s_cU_c$가 매우 궁금했는데, 고민해보니 각 $U_c$의 channel간에 중요도를 $S_c$에 값에 따라 조절하는데 이 중요도를 가중치로 부여하게 되는 것이다. 즉, $S_c$의 값의 비율에 따라 중요한 channel에 더 높은 가중치를 부여하게 되는것이다.

그러면 수식을 다 살펴봤는데, 어떻게 가중치를 출력하여 중요도를 추출하는지 궁금하지 않은가?? 그래서 알아보겠습니다.

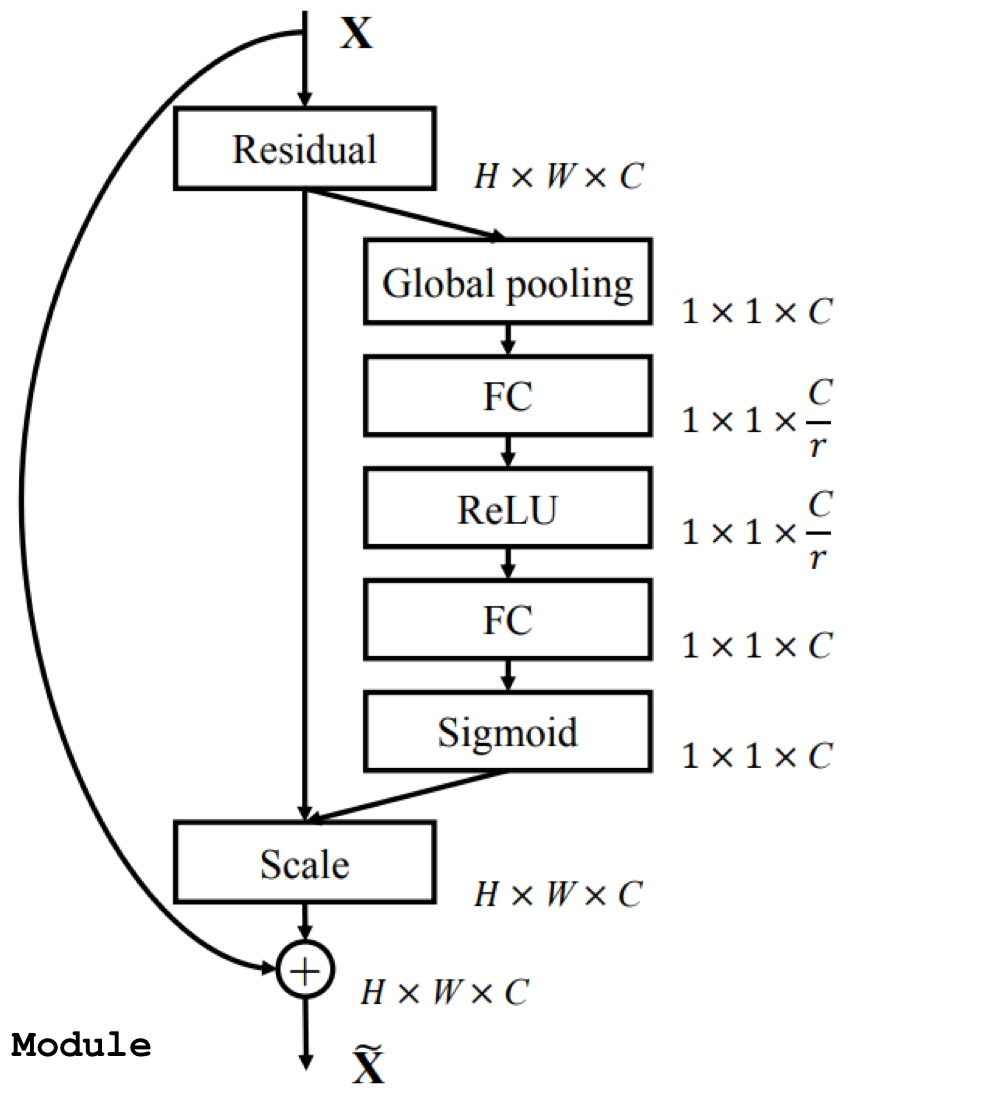
도식화한 것을 설명하자면, Residual은 conv연산을 취한 output값이다. 이 값을 차원 축소를 하기 위해 GAP을 적용하고 FC에 넣는다. FC의 output node는 Residual의 output channel C를 scale factor r로 나누어줌써 output node는 c/r이 되는 것이다.

다시 FC에 들어가서 residual의 output channel값과 맞춰주기 위해 output node개수를 C개수로 맞추어주고 FC의 output값은 softmax를 지나니 확률값이되는데 이 값을 다시 sigmoid함수를 넣음으로서 scale해준다고 한다.

근데, 나는 여기서 왜 첫번째 FC의 output값을 ReLU로 넣는지 이해가 되지 않아 찾아봤더니 channel간에도 반드시 비선형성을 가해주는 것을 의도했다고 하는데, 축소시킨 channel에서 ReLU로 channel간의 관계를 살펴본 것인데 이 값의 범위가 0~1값으로 나오니 channel별로 Input data와의 상호관계를 알 수 있는 것이다.

예를들어 축구공의 data가 들어오면, 어떤 filter는 모양을 체크하고, 다른 filter는 무늬를 체크하는 filter일 수 있다.
그러면 여러개의 filter중에서 저 2개의 filter가 학습하는데 중요한 filter의 역할이니 더 높은 가중치를 부여하게 되는 것이다.

ResNeXt

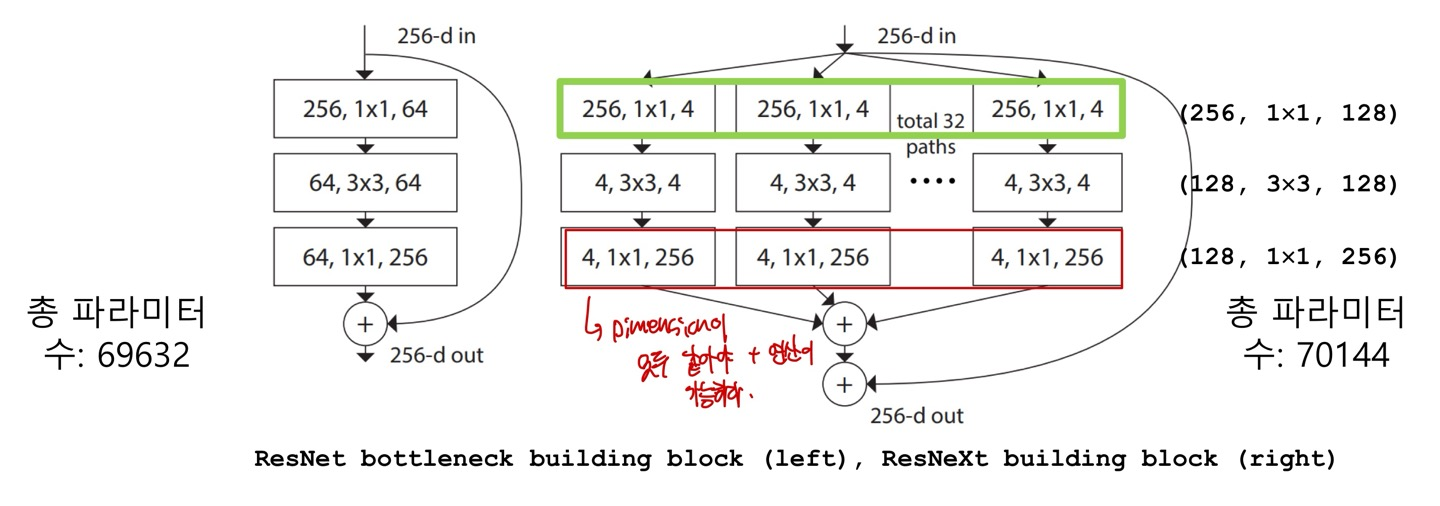
ResNeXt는 기존 ResNet의 block 개수를 C개로 늘려서 학습한다. 이때 C를 Cardinality라고 하며 Hyperparameter이기 때문에 사용자가 직접 입력해줘야한다.

왼쪽이 ResNet이고 오른쪽이 ResNeXt인데 (256, 1x1, 4)는 (input channels, filter size, output channels)를 의미한다. layer마다 다르겠지만 여기서는 32개의 block(path)가 존재한다고 하며 이후 ResNet과 마찬가지로 입력값 x를 더해주게 된다.
이때 각 path에서는 나중에 concat해야하기 때문에 이후 1x1 conv연산을 통해 channel수를 맞춰주게 된다.

여기서는 입력 channel 256개를 32개로 분할하여서 group conv연산을 해줬다고 한다.
group convolution로 했으니 각 channel수가 8개 있는 (h,w,8) 32개를 group conv연산 해줬다는 것이다. 이를 통해 parameter를 줄일 수 있다고 한다.