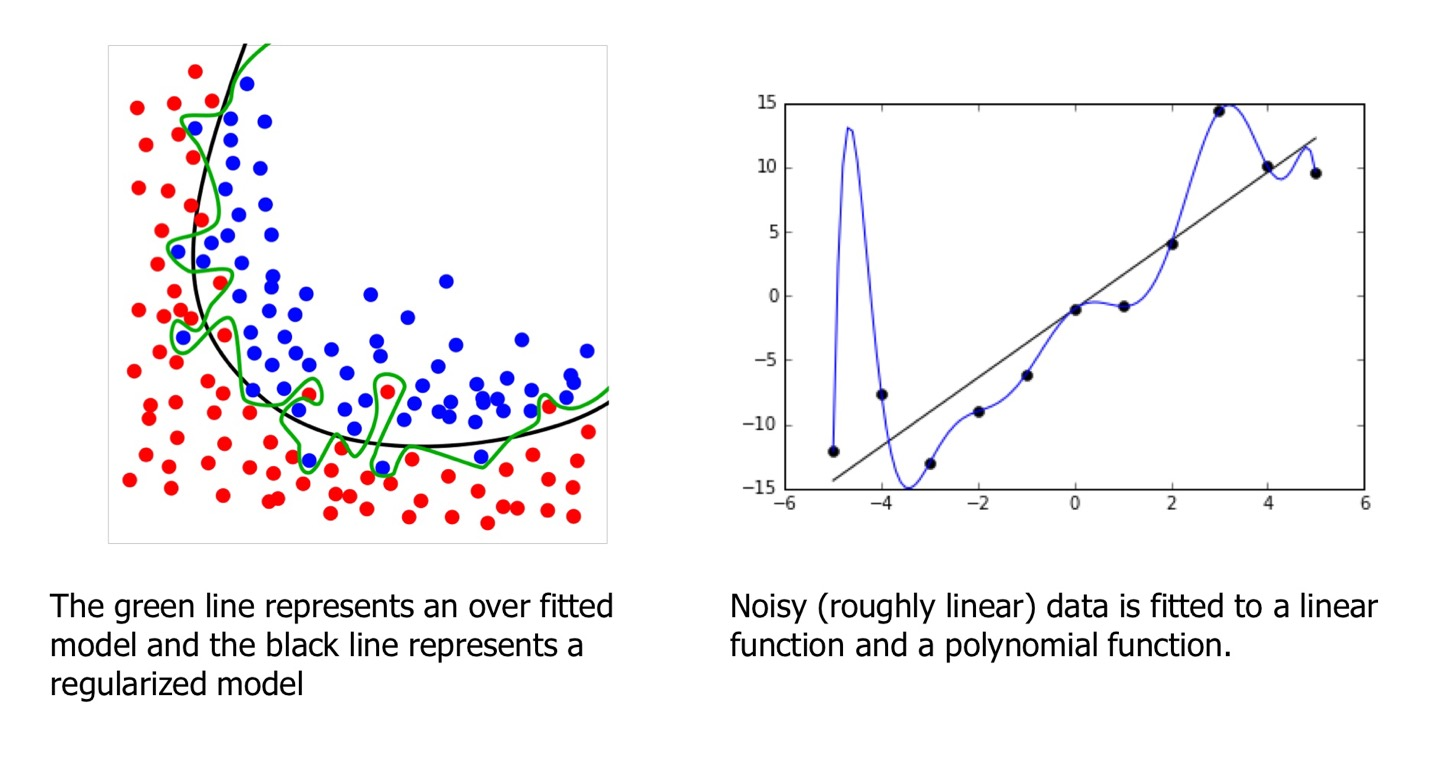
Overfitting이란, 신경망이 훈련 데이터에만 지나치게 적응되어, 그 외의 데이터에는 제대로 대응하지 못하는 상태를 말합니다.
훈련 데이터에 지나치게 적응되었다는 말은, 훈련 데이터에 있는 Noise와 Detail한 내용까지 세세하게 학습하기 때문에 훈련 데이터 외의 다른 데이터를 inference한다면 성능 예측이 떨어지게 된다.

---

Bayesian

시대가 발전해가면서 큰 모델을 더 많은 데이터로 학습을 진행합니다.
하지만, 모델이 커질수록 해석하기 어렵고 모델의 출력값을 얼마나 신뢰할 수 있는지 알 수 있는지 알기 어렵습니다.

우리는 모델을 학습시키고 Inference할때 입력값으로 학습하지 않는 데이터가 입력으로 들어오는 경우에는 모델이 학습하지 않은 데이터를 추론할 이유가 없다. 즉, 학습하지 않은 데이터가 입력으로 들어오는 것을 모델이 안다는 것이 매우 중요한 문제이다.

이러한 알지 못하는 데이터, 즉 잘 모르는 상황을 사전에 알고 있다면 이러한 Over-confidence와 같은 문제를 방지할 수 있게 된다.

Over-confidence란, 모델이 예측을 매우 확신하고 불확실성을 고려하지 않은 것을 말한다.

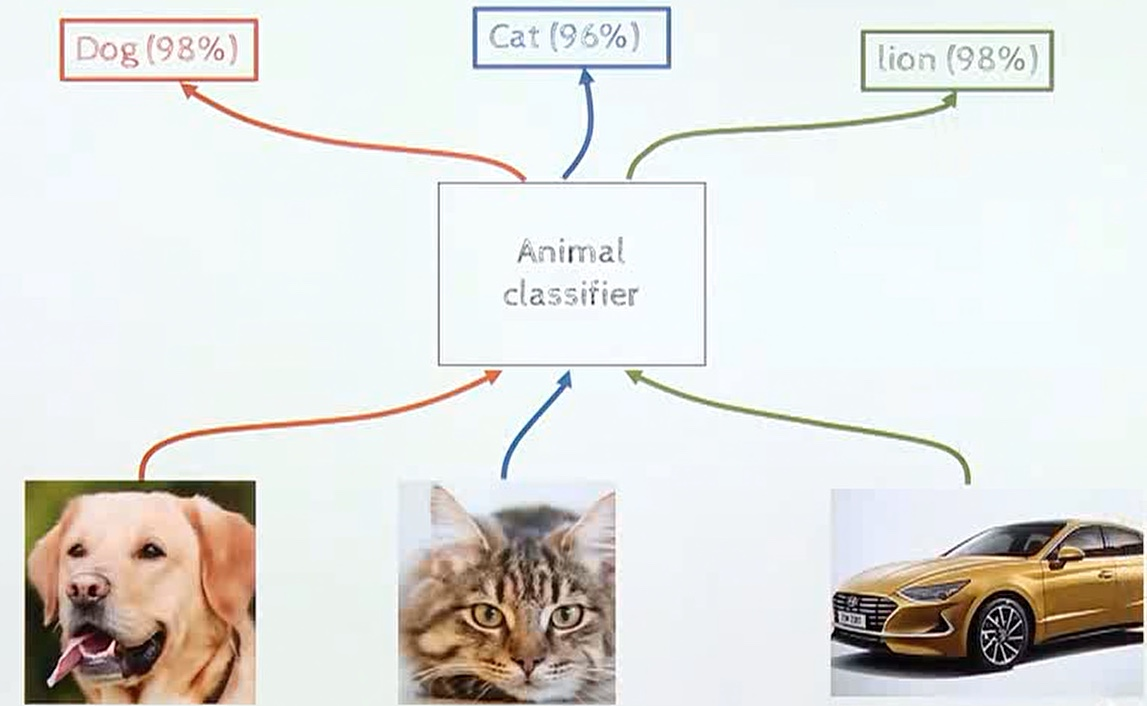
위 그림을 보게 되면, 동물 데이터로 학습한 Neural Network가 자동차를 입력값으로 주게 되면 Inference의 출력값을 Lion(98%)로 답변한다. 이러한 문제는 앞서 딥러닝 기반 인식 시스템의 over-confidence의 문제가 있다.

따라서 over-confidence의 문제는 불확실성(Uncertainty)를 고려하지 않았으므로, 불확실성을 고려할 수 있는 딥러닝 시스템을 구축하는 것이 매우 중요하다.

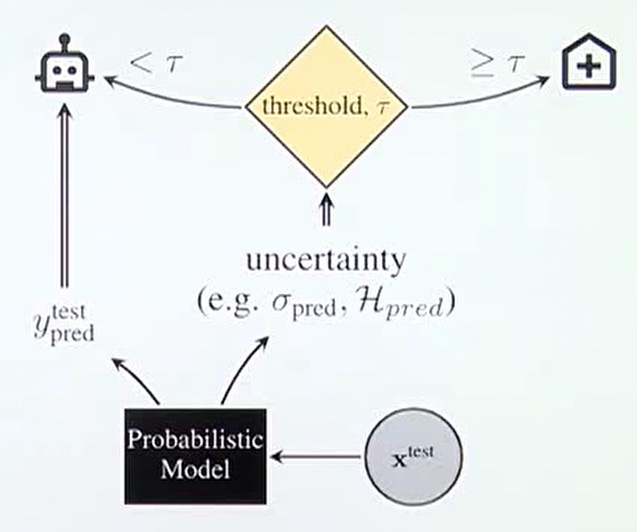
모델이 입력을 받을때 y(test pred)의 출력값과 uncertainty(불확실성)까지 출력하게 합니다. 만약 불확실성이 어떤 임계치(T)의 값을 넘는다면 출력값 y에 대한 별도의 검토가 이루어지게 합니다. 이러한 불확실성을 검토하게 되면서 자율주행, 의료 등의 불화실성에 매우 민감한 System에 사고를 예방할 수 있게 됩니다.

빈도주의 관점 VS 베이지안 관점

동전을 던지는 문제가 있다고 하자

빈도주의 관점에서는 동전을 무한히 던지면 앞면이 나올 확률은 0.5에 수렴하게 된다. 왜냐하면 무한히 던졌을때 나온 횟수가 전체의 50%에 수렴하기 때문이다.

수식으로 나타내면 p(θ) = $\frac{1}{2}$ 이다.

빈도주의 관점에서는 횟수를 세는 접근 방식으로 확률을 측정하는 방법인데 고정된 참 값의 확률을 찾아가게 된다.

베이지안 관점에서는 확률 자체를 "불확실성"으로 바라봅니다.
위의 빈도주의 관점에서는 앞면이 나올 확률을 50%라고 단정 짓지만, 베이지안 관점에서는 앞면 나올 가능성이 50%정도 라고 결론 짓습니다.
불확실성을 내포합니다.

따라서 베이지안은 불확실성을 내포한 확률 분포를 찾는 것이 목적입니다.

빈도주의에서는 확률값이 고정되어 있어서 어떤 확률값에 variance가 없이 고정 되지만, 베이지안에서는 정해진 확률값이 없이 분포로 나타내고 이 분포에는 variance가 존재하므로 불확실성을 내포한다.

즉, variance를 통해서 불확실성을 정량화(수치적으로 표현)한다.

동전의 앞면이 나올 확률이 0.5의 사전 지식으로 앞면 나올 확률이 0.5에서 가장 높은 likelihood를 가지게 됩니다.(Prior Distribution)

앞면 3번 뒷면 2번이 나오게 되면 확률 분포의 가장 큰 likelihood가 0.5보다 큰 쪽으로 옮겨지도록 업데이트 된다.(Posterior Distribution)

베이지안의 핵심은 불확실성을 나타내는 확률분포로 업데이트 된다는 것 입니다.

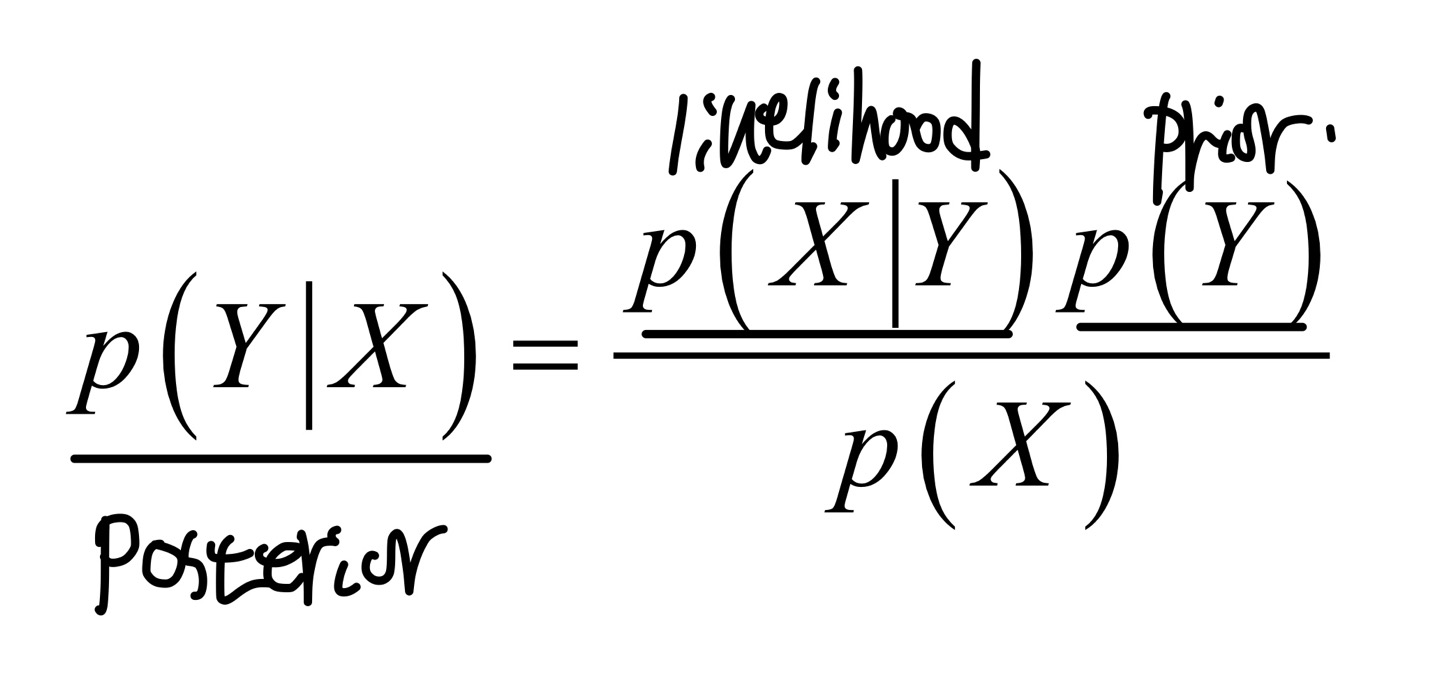
p(Y|X)[Posterior] : likelihood값을 이용하여 prior->posterior로 업데이트 한다.
p(Y)[Prior] : 새로운 데이터 X를 관찰하기 전에 알고 있는 사전 분포이다. 앞에서 상식적으로 알고 있는 앞면 나올 확률 0.5를 의미한다.
P(X|Y)[Likelihood] : 현재 모델이 얼마나 데이터를 잘 설명하는지 나타내는 정량화 된 값이다. 빈도주의에서 살펴본 확률 표현 방법과 같다. 3/5를 의미한다.

문제

건빵 2봉지를 샀다. 그래서 별사탕도 2봉지다. 첫번째 봉지에는 하얀별사탕이 10개, 분홍별사탕이 30개 들었고, 두번째 봉지에는 각각 20개씩 들었다. 두봉지의 별사탕을 하나의 접시에 담고, 눈을 감은채 별사탕하나를 집어들었다. 눈을 뜨고 집어든 별사탕을 지그시 살펴보니 분홍별사탕이다. 이 별사탕이 첫번째 봉지에서 나왔을 확률은?

별사탕이 첫번째 봉지에서 나올 확률이니 P(Y|X)에서 X를 별사탕이 나올 확률, Y를 첫번째 봉지를 고를 확률로 정의하면 된다.

그렇다면 P(Y|X) = $\frac{P(X|Y)P(X)}{P(X)}$ 가 된다.

P(X) = $\frac{50}{80}$ = $\frac{5}{8}$
P(Y) = $\frac{40}{80}$ = $\frac{1}{2}$
P(X|Y)는 첫번째 봉지를 고르고 별사탕을 뽑을 확률이니 P(X|Y) = $\frac{30}{40}$ = $\frac{3}{4}$ 이 된다.

베이지안 공식에 넣어 대입하게 되면 결과는 0.6이 나온다.

---

L2 Regularization(Ridge)

L2는 기존에 있는 손실함수에서 L2 norm을 적용한 변형된 손실함수이다.

Ridge를 나타내면 다음과 같다.

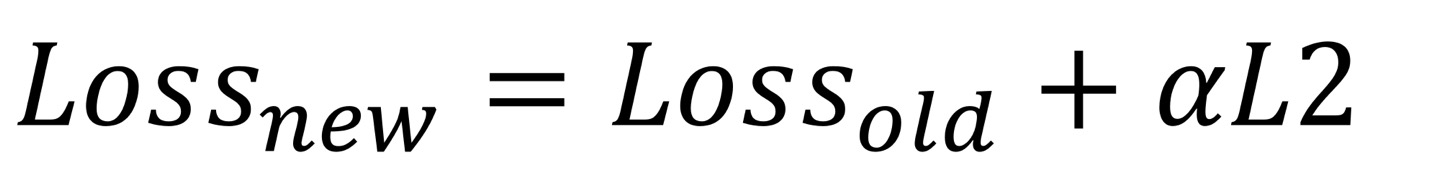
기존 손실함수 값을 구하고, 그 값에서 신경망에 있는 모든 가중치를 제곱하여 더해서 새로운 LOSS값이 나오게 된다. 이 식을 Ridge라고 한다.

경사하강법을 통해서 가중치를 업데이트하는 과정을 보자
여기서 ε는 학습률(Learning Rate)를 의미하고 α는 hyperparamter로 조절할 수 있는 변수이다.

이러한 L2를 이용하면 weight decay(가중치 감소)와 같은 효과를 얻을 수 있다.
이 효과는 다음과 같다.

• Variance의 크기를 작게 하여 overfitting 완화한다.
• 가중치의 크기에 따라 가중치 값이 큰 값을 더 빠르게 감소시킨다.
• 가중치의 크기에 따라 가중치의 penalty 정도가 달라지기 때문에 가중치가 전반적으로 작아져서 학습 효과가 L1대비 더 좋게 나타난다.

---

L1 Regularization(Lasso)

L1은 기존에 있는 손실함수에서 L1 norm을 적용한 변형된 손실함수이다.

Lasso를 나타내면 다음과 같다.

기존 손실함수 값을 구하고, 그 갑셍서 신경망에 있는 모든 가중치의 절대값을 더해서 새로운 Loss값이 나오게 된다. 이 식을 Lasso라고 한다.

경사하강법을 통해서 가중치 업데이트 과정을 보자
여기서 α는 hyperparameter이다.

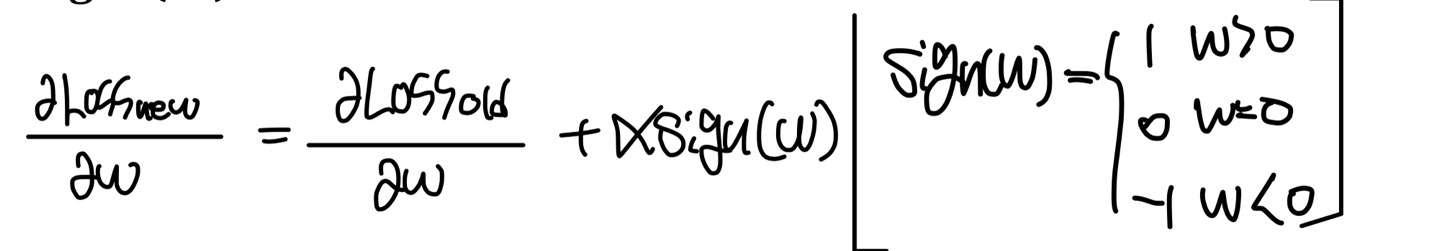
sign(w)는 |w|을 미분한 값(기울기)를 의미합니다.

이러한 L1을 이용하면 L2와 마찬가지로 weight decay(가중치 감소)와 같은 효과를 얻는다.
이 효과는 다음과 같다.

• 원하는 가중치만 남길 수 있는 feature selection 역할을 할 수 있다.
• 가중치의 크기에 상관없이 부호에 따라 일정한 상수 값을 빼거나 더해준다.

---

Dropout

Dropout은 신경망의 hidden layer의 일부 노드를 생략하여 학습합니다.
신경망이 복잡해지면 weight decay만으로 대응하기 어렵기 때문에 dropout기법을 사용합니다.

다음 아래의 내용은 블로그를 보고 설명과 함께 덧붙여 작성하였습니다.

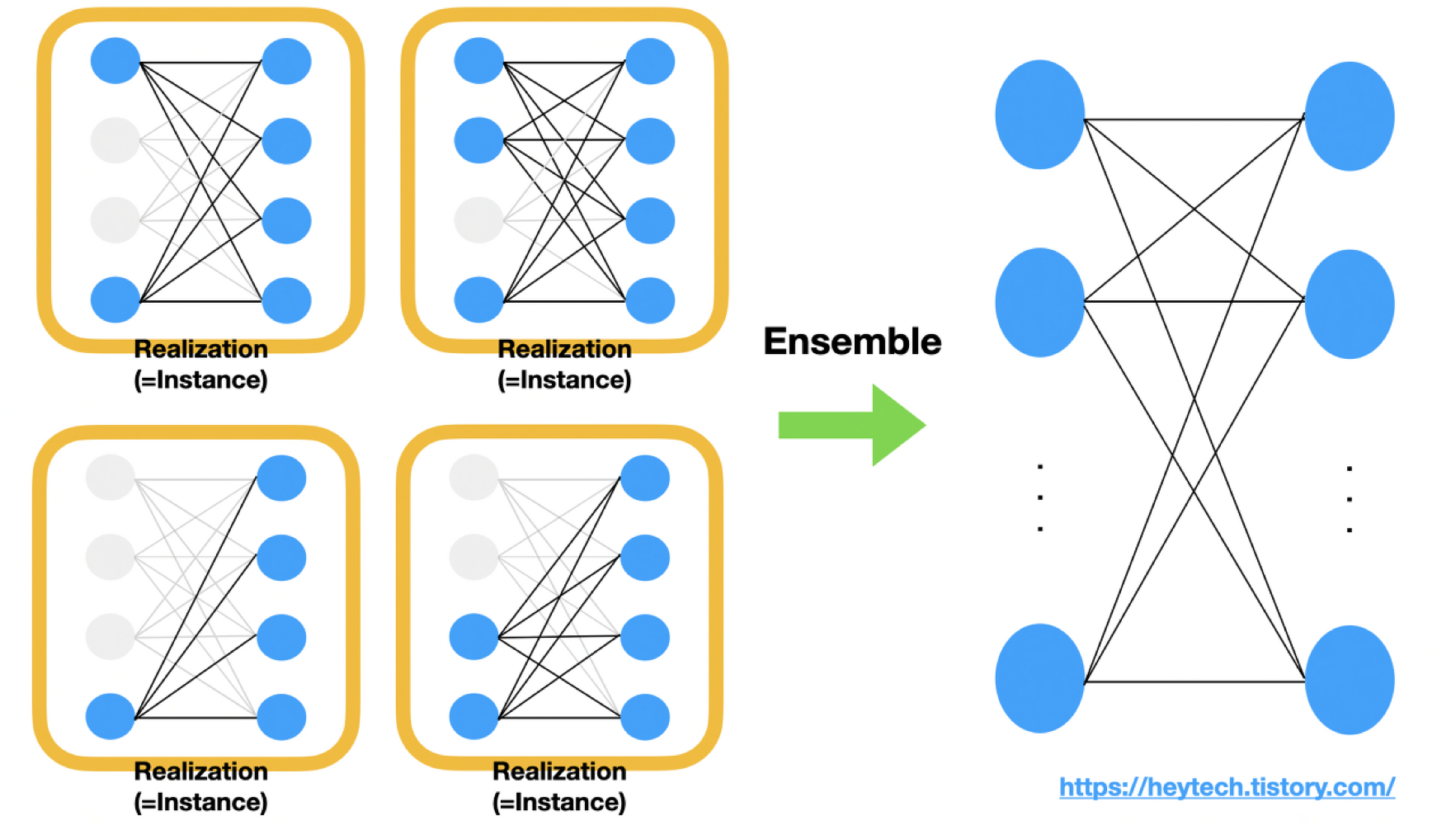
위의 노란색 박스로 있는 신경망은 Realization or Instance라고 불리우는데, 이 신경망은 dropout이 random한 확률로 노드가 지워진 것을 볼 수 있다.

만약 위의 4개의 Realization이 optimal한 출력값을 낸다고 가정하고 각 Realization 출력값의 평균을 매기면 오른쪽과 같은 최적화된 전결합층을 얻을 수 있다. 즉, 가중치 어느 하나 편향되지 않고 학습된 데이터의 일반화 된 값을 얻을 수 있다는 것이다.

한가지 예시를 들어보겠다.

어느 특정 가중치가 출력값에 가장 큰 상관관계가 있다고 가정해보자
만약 dropout을 적용하지 않는다면 상관관계가 큰 가중치가 가장 크게 설정되어 나머지 가중치는 제대로 학습하지 못하게 된다
하지만 dropout을 적용하였고 출력값과 상관관계가 큰 가중치를 지우고 모델이 optimal한 출력값을 얻는다면 해당 상관관계가 큰 가중치만으로 출력값을 좌지우지하는 overfitting을 방지하고 나머지 가중치도 종합적으로 확인이 가능하기 때문에 모델의 일반화(Generalization)이 가능하게 된다.

이렇게 dropout을 통해 가중치들의 co-adaption완화가 가능하다.
정확히 말하자면, 어떤 노드가 다른 특정 노드에 의존적으로 변화하는 것으로 어떤 가중치의 상관관계가 크게 되면 그 상관관계가 큰 가중치만을 크게 학습하게 된다. 그러면 다른 영향력이 낮은 가중치들은 상관관계가 큰 가중치에 의존적으로 변화하게 되어 불필요하게 되어버린다.(Computing power와 Memory 등의 낭비가 일어난다.)

Mini-batch 학습 시 dropout을 적용하게 되면 각 batch(batch_size)별로 dropout이 적용되게 된다.(매우 중요)

위에서 각각 Realization의 출력값의 평균을 매기면 최적화된 전결합층을 얻을 수 있다고 말씀드렸는데, 이것은 "앙상블 학습" 합니다.

앙상블 학습은 개별적으로 학습시킨 여러 모델의 평균을 내어 추론하는 방식인데, 이 학습을 수행하면 신경망의 정확도가 몇% 정도 개선된다는 것이 실험적으로 알려져 있습니다.

앙상블 학습은 dropout과 매우 밀접합니다. dropout을 통해 random하게 노드를 삭제하기 때문에 batch마다 새로운 모델을 학습시키는 것으로 해석할 수 있게 됩니다.(batch마다 dropout을 적용한 모델 생성한다고 생각하면 된다.)
테스트(Test)때에는 노드의 출력에 삭제한 비율을 가중치에 곱하기 때문에 앙상블 학습에서 여러 모델의 평균을 내는 것과 같은 효과를 얻습니다.
더 정확히 말하자면 dropout은 steps에 따라 모델이 새롭게 생성되고 이 모델을 통하는 것과 더불어 테스트 때 노드의 출력에 삭제한 비율을 가중치에 곱하는 것으로 여러 모델의 평균을 내는 것과 같은 효과를 얻는 것 입니다.

즉, dropout은 앙상블 학습과 같은 효과를 하나의 모델로 구현했다고 생각할 수 있습니다.
(앙상블 기법도 overfitting을 예방하는 한가지 방법입니다. 머신러닝 시리즈에 설명되어있습니다.)

---

Data Augmentation

• Data Augmentation이란, 부족한 훈련데이터셋을 여러가지 방법으로 augment하여 실질적인 학습 데이터의 규모를 키우는 방법이다.

• 데이터를 늘린다는 것은 overfitting을 줄일 수 있다는 것을 의미한다. 예를들어 가지고 있는 데이터셋이 실제 상황에서의 입력값과 다른 경우, augmentation을 통해 실제 입력값과 비슷한 데이터 분포를 만들 수 있다.

• 모델이 실제로 환경에서 잘 동작할 수 있도록 도와준다.

• CV의 성능을 향상시키는 기술의 일종이다.

Data Augmentation기법은 다음과 같습니다.

• Translation
• Rotation
• Stretching
• Shearing
• Flip
• Random crop
• Scale
• Color jittering : 명도, 채도 등의 random 변화
• Elastic distortion : 다양한 displacement vector(이동 벡터)를 이용하여 이미지의 Pixel의 위치를 이동하는 것으로 이미지를 왜곡한다.

---

Batch Normalization

다음 Batch Normalization의 설명은 이 JINSOL KIM(Batch Normalization)을 정리하여 설명합니다.

Batch

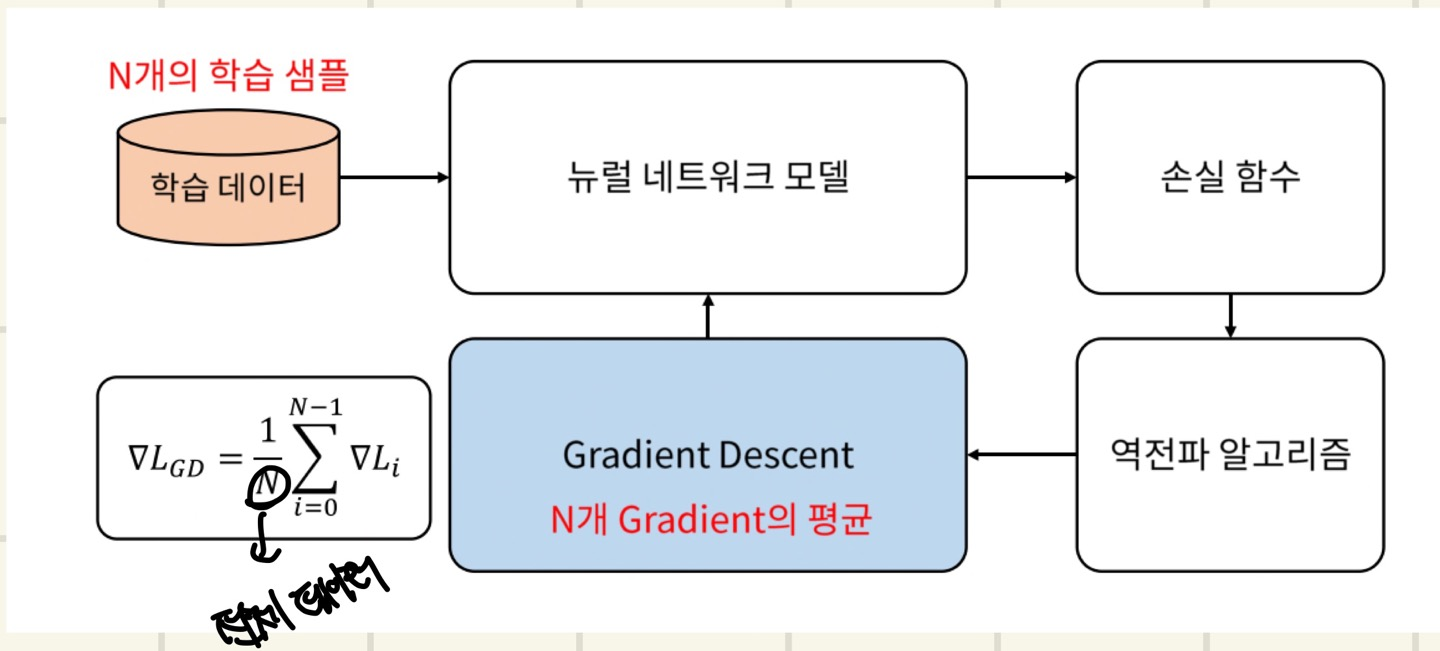
경사하강법에서는 gradient를 1번 update하기 위하여 모든 학습 데이터를 사용합니다. 하지만 데이터가 무수히 많을때는 현실적으로 불가능하기 때문에(대표적으로 메모리 문제) batch 단위별로 나눠서 학습을 하는 방법이 일반적입니다.

위 식의 N은 데이터의 개수를 뜻하고 손실함수 값의 N을 나누어 평균을 구한다.
모든 데이터를 사용해서 1개의 w개의 차원의 손실함수 그래프를 얻어, 학습을 진행하게 된다.

모든 학습 데이터로 가중치를 업데이트 하지 못하기 때문에, batch단위로 나눠서 학습을 하는 것이 일반적인 방법이다.
steps만큼의 손실함수 그래프가 존재하고, 학습을 진행하게 된다.

SGD(Stochastic gradient descent)

앞서 설명한대로, 모든 학습데이터를 사용하여 가중치를 update하는 것은 현실적으로 한계에 부딪히게 된다. 그러므로 우리는 학습데이터를 일정하게 자른 batch단위별로 학습을 진행하게 된다.

우리는 이것을 SGD라고 부르게 되며, 1번 update하기 위해서 batch_size만큼만 사용하여 가중치를 업데이트하게 된다.
(batch : gradient를 구하는 단위)

Purpose of Batch Normalization

Internal Covariant Shift

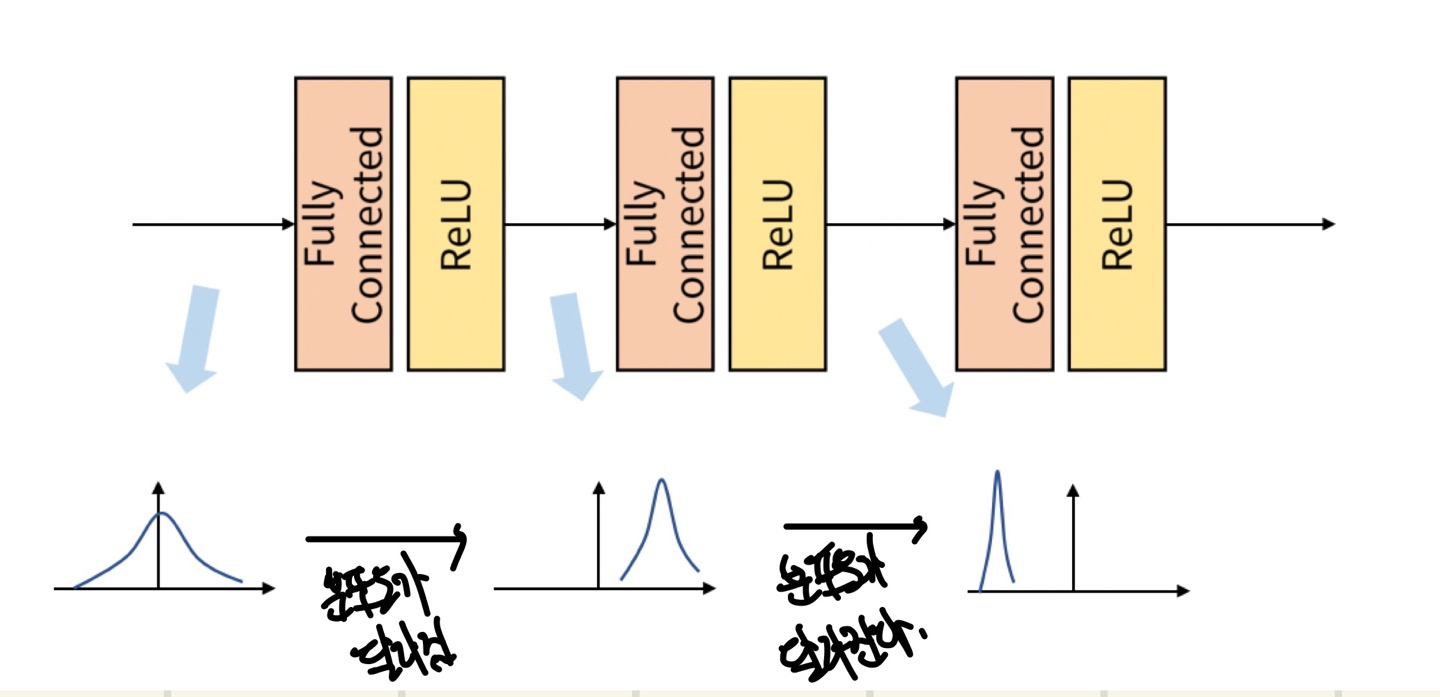
batch 단위로 학습을 하게 되면 논문에 나와 있는 Internal Covariant shift 문제가 일어나게 된다.

Internal Covariant shift란, 학습 과정에서 Layer별로 입력의 데이터 분포도가 달라지는 현상이다.
이는, 각 Layer에서 노드마다 입력값을 받게 되고 연산을 거치게 되면 연산 전/후에 데이터 간 분포도가 달라질 수 있게 된다.
이와 유사하게 batch단위로 학습을 하게 되면 batch 단위간에 데이터 분포의 차이가 발생할 수 있다.

만약, 학습을 진행하면서 데이터의 분포도의 변형이 누적되어가다보면 각 Layer에서는 입력되는 값이 전혀 다른 유형의 데이터라고 받아들일 수 있게된다.

데이터의 분포도가 달라지는 원인은 오차역전파의 과정에서 gradient vanishing으로 원인을 규정하고 있다.

우리는 이러한 문제를 Batch Normalization을 통해 문제를 해결할 수 있다.

Gradient Vanishing / Gradient Exploding

경사하강법의 식을 보겠습니다.

w <- w - α$\frac{∂L}{∂w}$가 되는데, 만약 MLP라면 $\frac{∂L}{∂w}$에서는 오차 역전파(Backpropagation)을 통해서 가중치가 Update 됩니다.

이 가중치는 신경망의 출력에 영향을 미치는 parameter이며, 이 w값의 변화량에 따른 출력값의 변화가 작다면 w의 학습은 제대로 이루어지지 않고, 또한 너무 크거나 작다면 gradient vanishing 또는 gradient exploding이 일어날 수 있습니다.

예시를 들어보겠습니다.

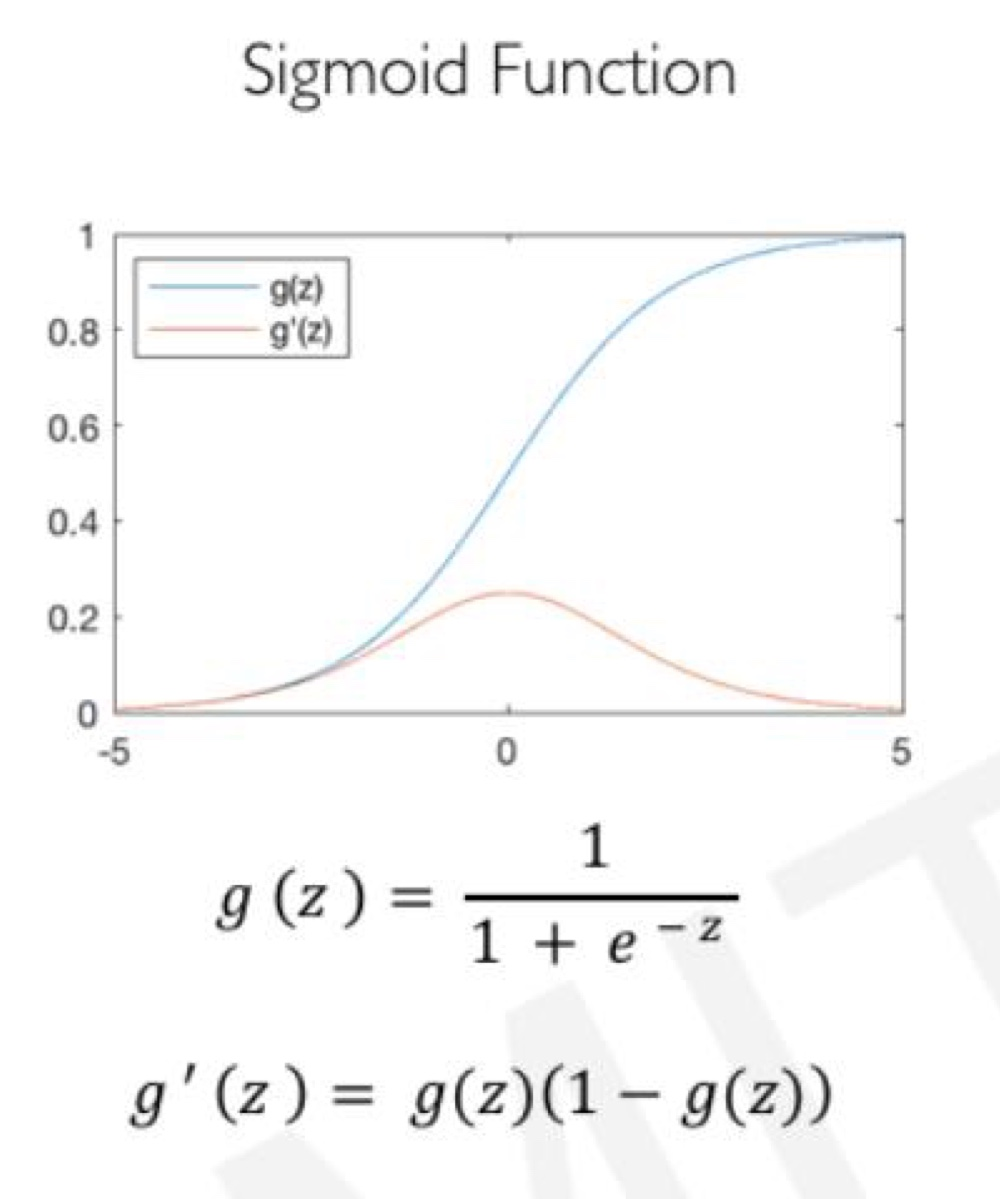
위의 그래프는 sigmoid 활성화 함수입니다.
sigmoid 함수의 치역은 [0,1]의 범위가 됩니다. 즉, 입력값이 아무리 크거나 작더라도 [0,1]에 mapping되어 출력값이 [0,1]의 값을 가지게 됩니다.

만약 MLP에서 첫번째 Layer에 입력값이 너무 크게 주게 된다면 오차역전파 과정에서 변화량의 값(기울기 값)이 0이 나오게 됩니다. 즉, 가중치가 update가 되지 않아서 학습이 제대로 이루어지지 않을 수 있게 됩니다. 이러한 변화량의 값이 0에 가깝게 나오는 것을 gradient vanishing현상이라고 불리웁니다.

이러한 문제점으로 우리는 ReLU의 활성화 함수를 쓰지만, 학습하는 전체 과정을 안정화 시키기 위하여 Batch Normalization기법도 함께 사용합니다.

Whitening

Batch Normalization이 있기 전에 최초의 해결 방안으로 각 layer에 들어가는 입력을 whitening할 수 있다.
whitening이란, 입력을 평균 : 0, 분산 : 1로 정규화 시키는 방식이다.

하지만 whitening을 진행하면서의 문제점이 존재한다.

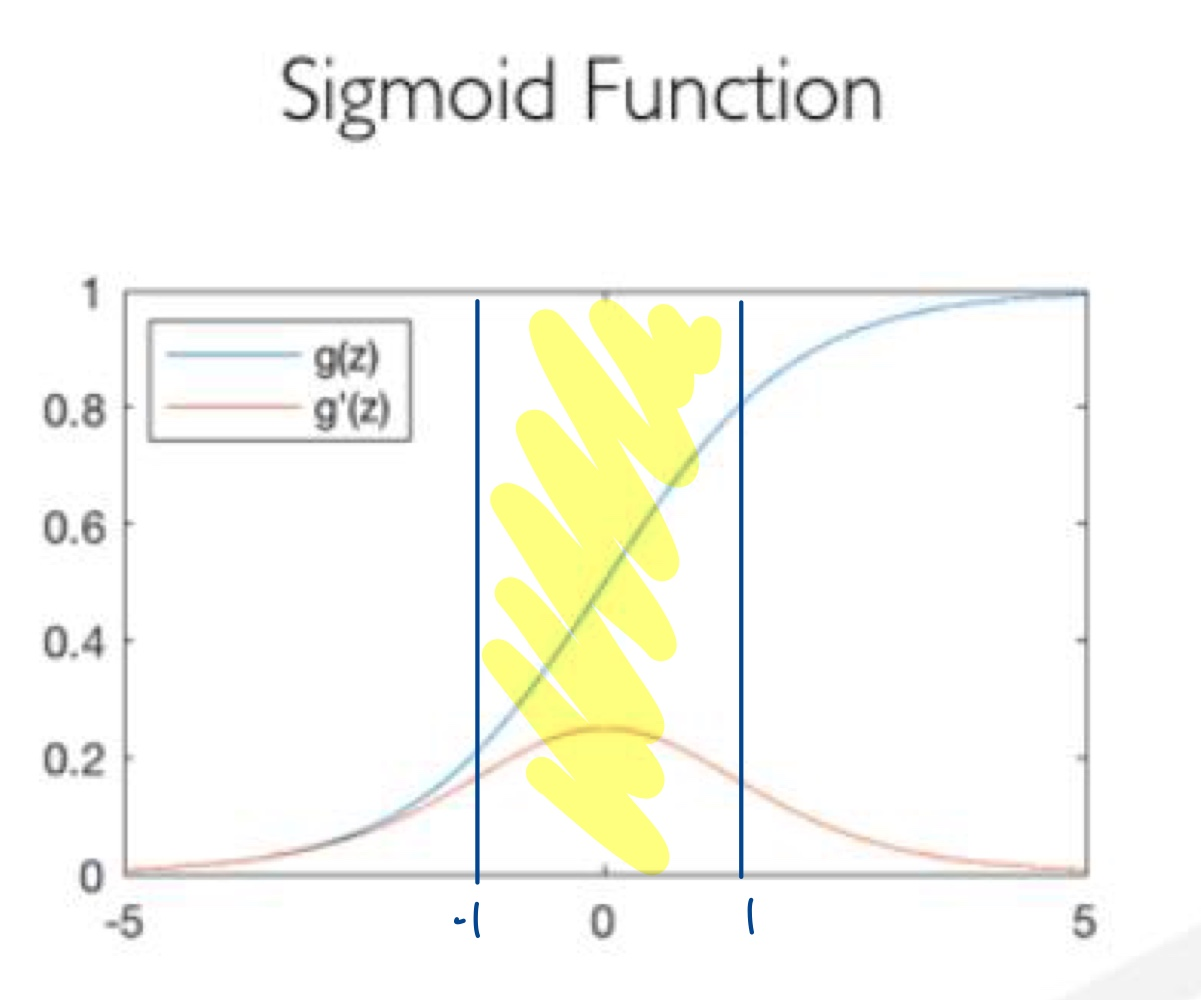
위의 활성화 함수인 sigmoid함수를 통해 문제점을 말하자면, 아래에서 설명하겠지만 Batch Normalization을 수행하고 활성화 함수에 값을 넣게 된다.
이와 마찬가지로 whitening의 결과 값을 활성화 함수에 입력값으로 넣게 되는데, 입력값의 데이터 분포도가 -1~1 사이 값에 위치하게 된다.

위의 sigmoid함수에서 노란색 색칠한 부분을 보게 되면, -1,1 사이 구간은 Linearity하며 활성화 함수를 통해 nonlinearity의 효과는 없어지게 된다는 것이 주요 문제점이다.

그래서 우리는 Batch Normalization을 통해서 γ(scaling),β(shift)을 통해서 Nonlineartiy의 문제점을 해결할 수 있게 된다.

또한 우리는 Bias의 대한 영향력도 감소할 수 있게 된다.

예시를 들어 설명하겠다.
우리가 weighted sum하여 얻은 값이 z(wx + b)라고 하자. 그렇다면 우리는 결과값이 다른 layer의 노드에 입력값으로 들어가기전에 평균을 0, 표준편차를 1로 만들어야 한다고 말했다. 그렇다면 우리는 z 즉, wx+b의 평균값을 빼주고 이 z에 대한 표준편차를 나눠줘야 한다.
하지만 평균값을 빼주는 과정에서 b(bias)의 영향력은 없어지게 되고 scaling(표준편차로 나눠주는 것)으로 나눠주는 과정까지 포함한다면 이러한 경향은 더욱 악화된다.

The Procedures of Batch Normalization

batch normalization은 whitening기법에 활성화 함수에 들어가기전에 scaling과 shift을 적용한 기법이다. 이를 통해 우리는 앞에 나와 있는 문제점을 보완할 수 있다.

👀배치 정규화는 학습 단계 / 추론 단계에서 다르게 적용된다.(중요)

학습 단계에서의 batch normalization

normalize하는 식에서 각 입력 값들의 평균을 빼주고 표준편차로 나누어주는 주게 되면 평균은 0, 분산은 1로 맞춰주게 됩니다.(z-score 기법과 같다.)
ε는 분모가 0이 되지 않도록 하는 값이며, 1e-5의 값을 가지고 있습니다.

batch normalization은 평균과 분산을 조정하는 과정이 별도의 과정으로 떼어지는 것이 아니라, 신경망 안에 포함되어 학습 시 평균과 분산을 조정하는 과정이 같이 조절된다는 점에서 whitening과 구별됩니다. 즉, γ,β는 오차역전파 과정에서 최적화가 진행되므로 parameter값에 해당됩니다.

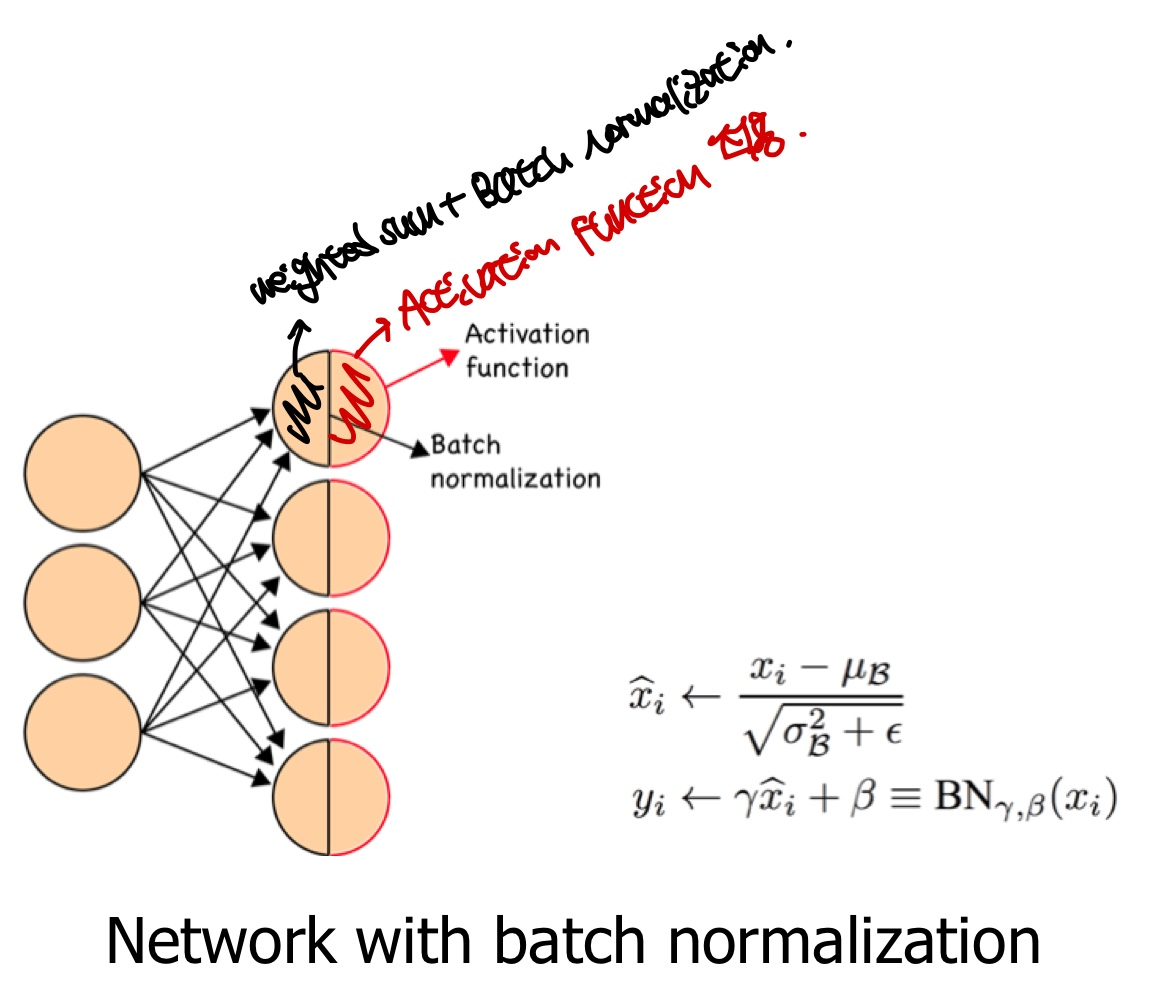
batch normalization이 적용되는 것은 Layer기준으로 적용되는 것이 아니라, Layer 내부의 노드 기준으로 Normalization을 하게 됩니다.

그러면 4개의 노드를 가지고 있는 Layer에는 4개의 batch normalization이 적용이 되겠네요.

추론(Inference) 단계에서의 batch normalization

Inference단계의 고민은 다음과 같다.

• mini-batch size
• 학습한 batch normalization기법을 활용하지 못한다.

Inference단계에서의 mini-batch size는 1일 수 있다. 왜냐하면 한 장의 이미지에 대해서도 결과 값을 내야하기 때문이다.
하지만 batch size가 1인 경우에는 평균과 분산값을 측정하지 못하게 된다. 왜냐하면 입력 데이터가 1개이기 때문여서 정규화를 진행하지 못한다.

우리는 기껏 학습한 γ,β 값을 활용하지 못합니다.
만약 우리가 inference의 대한 데이터를 통해 평균과 분산을 구해주고 정규화를 시켜준다고 하고 이것을 γ,β을 통해 scale과 shift를 시켜준다고 하게 되면 학습과정에서의 γ,β지식을 활용하지 못하는 꼴이된다.

왜냐하면, inference의 batch마다 평균과 분산 값이 서로 다를테니 값이 튀게 되기 때문이다.

그렇기 때문에, 우리는 평균과 분산은 학습 데이터를 대표하는 값을 사용해야한다.

따라서 우리는 inference를 하기 위한 최적의 평균값과 분산값을 구하기 위해서 학습 데이터 전체 mini batch의 이동 평균(moving average)를 구해야한다.
이동평균을 사용하는 이유는 batch만큼의 데이터가 각 layer를 거치면서 학습이 진행될거고 점차 이상적인 분포로 향해 나아가고 있을 것이다.
따라서, 우리는 뒤에서 나오는 mini batch의 평균과 분산일수록 학습 데이터 전체를 대표한다고 볼 수 있게 됩니다.