Camera Calibration이란?
실제로 우리가 시각적으로 보는 3차원의 공간을 2차원 상에서 어디에 맺히는지 정확하게 알기 위한 것 이다.
이러한 작업이 왜 필요하냐면, 실제로 카메라의 Intrinsic Parameter(내부 파라미터)와 Extrinsic Parameter(외부 파라미터)가 존재하게 되는데 이 2가지의 parameter로 인해서 우리가 실제적으로 보는 것과 카메라로 찍은 이미지가 다를 수 있다는 것이다.
따라서 Camera Calibration이란 위의 2가지 parameter를 구하는 작업이라고 생각하면 된다.
이러한 parameter를 구하게 되면 3D에서 2D, 2D에서 3D로 복원할 때 정확한 위치로의 계산이 가능해진다고 한다.(2D에서 3D는 이해는 안되지만, 알게 된다면 수정하겠습니다.)
Parameter
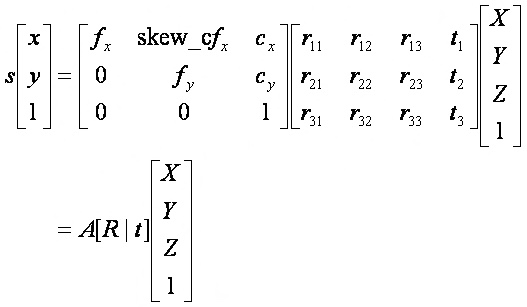
영상 좌표계에서도 보았던 것과 skew_c를 제외하고 비슷한 식을 보여주는데 차근차근 알아보자
(s는 카메라로부터 떨어진 z 거리를 의미한다. 스칼라 값임)
위의 vector는 월드 좌표계(World Coordinate)에서의 한 점의 좌표이다.
위의 matrix는 [R|t]로 불리우며 월드 좌표계를 카메라 좌표계로 변환 시키기 위한 rotate / translate 변환 행렬이다. 이것이 카메라 외부 파라미터로 Extrinsic Paramter이다.
위의 Matrix는 Intrinsic Parameter이다.
정리하자면, [R|t]와 월드 좌표계를 곱하게 되면, 월드 좌표계에서 카메라 좌표계로 변환하게 되고 카메라 좌표계에서 A를 곱하게 되면 Image Plain에 projection한 좌표값들을 알 수 있게 된다.
따라서 위의 A와 [R|t]를 합쳐서 Camera Matrix 라고 불리우게 된다.
Extrinsic Parameter는 Camera의 설치 높이, 방향 등 카메라의 외부 공간을 의미하고, Intrinsic Parameter는 Camera의 초점 거리(Focal Length), aspect ration 등 카메라 자체의 내부 공간을 의미한다.
Intrinsic Parameter
내부 파라미터는 다음과 같이 3가지가 존재한다.
-
초점 거리(Focal Length) :
-
주점(Principal Point) :
-
비대칭 계수(Skew Coefficient) : skew
초점 거리(Focal Length)
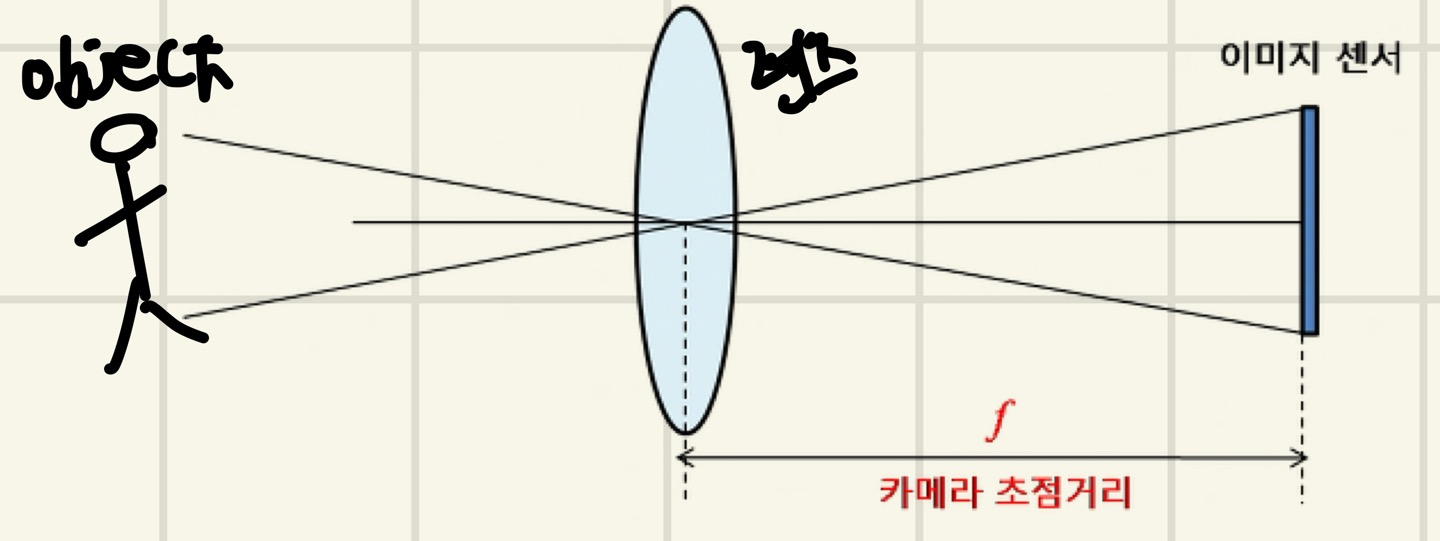
먼저 Camera Calibration의 초점 거리의 정의는 렌즈 중심과 이미지 센서(CCD, CMOS)와의 거리를 의미한다.
여기서 렌즈와 이미지 센서는 카메라의 내부에 있는 시스템이다.
- 렌즈 : 광을 집중시켜 이미지 센서에 해당 광을 전달하는 역할
- 이미지 센서 : 렌즈로 모인 빛을 전기적 신호로 변환하여 디지털 이미지를 생성한다.(Pixel값을 생성한다.)
렌즈에서 광 정보를 받은 이미지 센서는 이미지의 pixel을 표현하기 위해 이미지 센서의 단위인 cell에서 pixel로 변환하는 과정을 거치게 되는데, 이 cell은 pixel에 그대로 mapping되기 때문에 초점 거리(f)가 pixel단위라는 의미는 초점 거리가 이미지 센서의 cell크기에 대한 상대적인 값으로 표현된다.
여기가 잘 이해가 되지 않을 수 있는데, 실제로 정확하게 보이는 것은 렌즈일 것인데 우리는 그 렌즈에서 본 이미지의 정보를 전기적 신호로 변환해야하기 때문에 어쩔 수 없이 이미지 센서에서 cell값을 pixel값으로 변형시켜야한다.
그렇기 때문에 초점 거리를 고려하지 않는다면 실제로 보이는 것보다 scale이 다를 수 있게 되는 것이다.
따라서 이미지 센서의 물리적인 cell간격이 다를 경우 A의 matrix에서와 같이 로 표현되며
=
=
필자는 cell의 가로방향이 resolution의 가로방향인줄 알았다..
현대의 카메라들은 cell의 가로와 세로의 크기의 차이가 없기 때문에 의 값이 같으므로 f라고 사용해도 무방하다고 한다.
만약, 이미지의 resolution을 로 낮추게 된다면 2x2의 이미지 센서의 cell이 1개로 합쳐져 1개의 이미지 pixel을 생성하게 된다.
그렇다면 값도 만큼 작아지게 되는 것을 잊지말자 매우 중요하다.
주점(Principal Point)
주점 는 카메라 렌즈의 중심에서 이미지 센서에 내린 수선의 발의 영상 좌표로 단위는 pixel을 이용합니다.
비대칭 계수(Skew Coefficient)
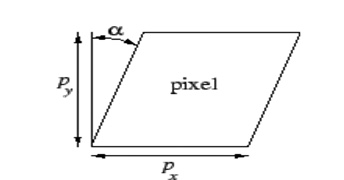
비대칭 계수는 이미지 센서의 cell이 기울어진 정도를 의미한다.
하지만, 현대 카메라는 cell의 기울어진 정도가 없다고 하며 비대칭 계수는 거의 고려하지 않는다고 한다.
따라서 비대칭 계수의 값은 0으로 봐도 된다.
카메라 좌표계에서 영상 좌표계로의 변환
과정 별로 차례대로 씁니다.
- 를 로 나누어주게 된다. 이것은 정규 좌표계로 변환하는 것이다.
- (u,v)를 f로 곱하면 Image Plane에서의 pixel값이 나오게 된다.
- Image Plane의 원점은 upper-left이기 때문에 실제 최종적인 영상 좌표는 를 더해줘야한다.
즉 영상 좌표계(x,y)는 다음과 같은 식을 지닌다.
X = +
Y = +
