Abstract

최근 Lane Detection의 관한 연구들은 특정한 상황만 놓은 method를 탐구하기 마련이다.
하지만, 이러한 method들은 complex한 topology lane(dense, forked, curved, etc..)을 다루기에는 쉽지 않다고 한다.

Dynamic Convolution이 나오고 나서, lane의 line을 location을 찾는 것에 핵심적인 key가 되었고 아주 좋은 performance를 보였다고 한다.
이러한 convolution기법으로 특정한 상황만 놓은 것에 국한되지 않고, topology lane을 어느정도 detect을 할 수 있었지만, 길고, 가벼운 network로 인해서 lane의 global structure를 찾기에는 어려움을 겪었다고 한다.

이러한 한계를 극복하기 위해서, transformer에 기반한 dynamic kernel generation architecture를 제안하였다. 이 method를 통해서 input img안에서 lane의 global structure를 모두 찾을 수 있었으며, occlusion과 lane intersection과 같은 lane을 detect할 수 있었다고 한다.

occlusion : lane이 object에 막혀서 보이지 않는 상황
lane intersection : 교차로, 차선 변경 지점

이를 통해, SOTA논문대비 OpenLane은 f1-score 63.4로 4.3이 상승했고, CurveLanes는 88.47로 2.37이 상승하였다고 한다.

---

Introduction

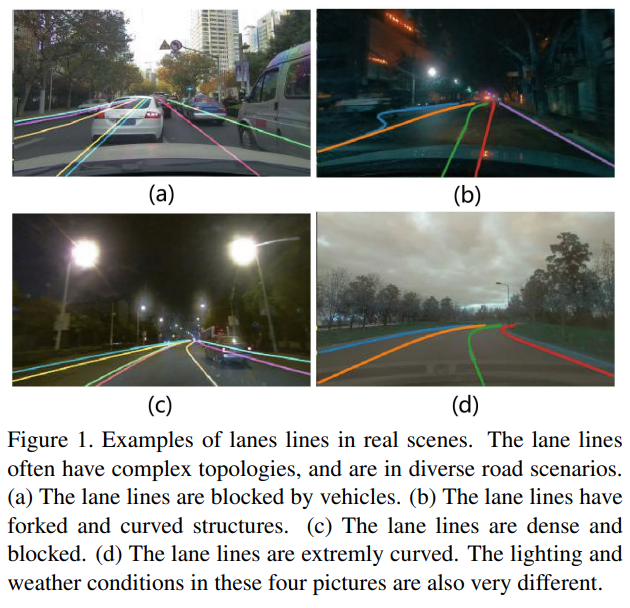
Lane Detection은 down streaming의 절차로 autonomous driving system에서 매우 중요한 절차이다.

down streaming : 다른 작업에서 중요한 절차로, 중간 처리 단계

또한, Lane Detection에서는 high speed를 매우 요하고 있다고 한다.

어쨋든, 전통적인 방법인 Hough transform을 통한 lane detection은 topology를 다루기에는 representation 능력이 매우 떨어진다. 거의 직선만 검출하기 때문..
따라서, CNN 즉, 딥러닝을 이용한 lane detection이 매우 뛰어나고 있다는 것을 발견했고 현재 detection에서는 거의 anchor box를 이용해서 object detection을 하게 된다.

마찬가지로, lane detection에서도 anchor box를 사용하여 lane을 detection 하기도 하며, parameter-based method도 사용한다고 한다.

하지만, 이러한 method들은 occlusion과 complex topology들을 다루기에는 매우 어렵다고 한다. (위의 Figure1이 좋은 예시가 될 것이다.)

anchor box를 사용하지 못하는 이유를 간략하게 말하자면, curved, forked lane들은 pre-defined anchor로 다루기에는 매우 어렵다고 한다. 즉, 미리 anchor로 lane의 location을 찾는 것이 어려운 것이다.
이는, lane이 다양한 환경에 놓여있어 어디에 있는지 찾기 힘들뿐더러 곡선이나 갈래진 차선은 보통 더 복잡하고 다양한 형태를 가지며, 이를 사전에 정의된 anchor로 다루기 어려울 수 있기 때문이다.

parameter-based method는 parametric한 curve를 fit하게 하는 것은 엄청 어렵다고 한다.
예를 들어, 엄청 나게 꺾인 lane을 예시로 들을 수 있다.

CondLaneNet은 dynamic convolution-based method를 사용하여 lane을 detection을 하였는데, lane의 starting point를 검출하는 것에 매우 performance가 좋았다고 한다.
이때 starting point란, 서로 다른 lane을 다르게 detection하는 것을 뜻한다.
하지만, 앞서 abstract에서 이야기했던 것과 같이, global information을 얻지 못하여 complex topology에서는 별로 였다고 한다.

condLSTR은 이를 해결하기위해, transformer-based dynamic kernel gerneration architecture를 고안하였다. (남은 논문의 설명은 abstract과 같기에 생략합니다.)

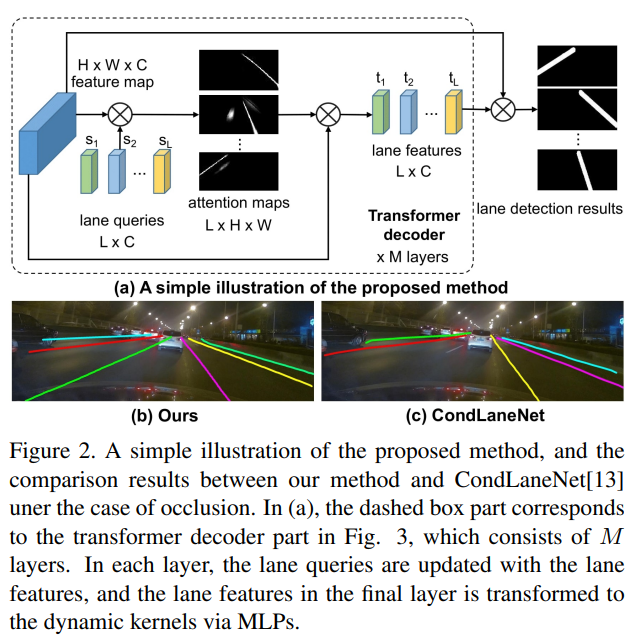
transformer-based dynamic kernel gerneration의 간략한 pipeline은 다음과 같다.

• Lane query로 불리는 parameter를 써, whole feature map을 통한 Lane Point를 찾는다.

• weighted sum으로 serached된 Lane Points의 feature들을 결합하여 각각의 line에 맞는 dynamic kernel을 생성한다.

• 생성된 kernel이 lane의 lines들에 global info를 capture한다.

lane queries는 annotated data와 다양한 lane lines들을 approximate할 수 있게 parametric하다. 아무튼, 다양한 차선 형태를 표현할 수 있는 것을 의미한다.

생성된 kernel은 각각의 lane에 heat map과 offset map이 생성되며, final lane은 post-processing 이후, heat map과 offset map을 생성하게 된다.

훈련중에는, bipartite matching loss이 계산되며, Hungarian algorithm을 기반으로 계산한다.

Bipartite Matching Loss

기존의 Architecture들은 indirect set prediction인 NMS, Region Proposal 등 hand-designed component들이 많이 고안되어왔다.
이는, 너무 많은 Bbox를 만들어내기 때문에, near-duplicate problem이 생겨, Region Proposal된 것 중, 가장 적합한 Region을 찾는 느낌이 더 가까웠다.

이는, Bipartite Matching은 hand-designed component없이, network자체에서 직접적으로 prediction하는 direct set prediction을 고안한다.
이를 위해, Matching Problem이 중요하게 작용된다.(1:1 Mapping을 목표로 한다.)

이러한 Matching Problem은 Hungarian Algorithm기반인 Hugarian Loss를 사용하게 된다. 이는 prediction, ground truth의 각각의 개수 N이 N-N Matching이 되기 위해서 각 group의 요소를 살펴보아야 한다는 것이다. 즉 N-N의 모든 경우의 수를 찾는 것이 된다.(더 쉽게 이해하려면 O(n^2)으로 이해하면 될 듯)

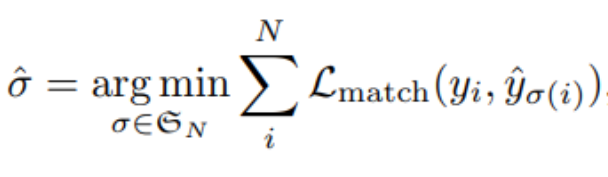
위의 식의 $σ^{hat}$은 ground truth와 최적의 Bbox를 고르는 작업이며, 이는 ground truth와 1:1로 matching이 되는 Bbox를 고르는 작업이라고 생각하면 된다. (1:1 matching이라는 것을 잊지말기)

$L_{match}$는 class prediction과 Bbox prediction loss들이 있으며, 일반적인 object detection의 loss와 비슷한 식을 구성하고 있다.

어쨋든, 여기까지만 정리하자면 ground truth와 최적의 bbox를 고르는데 network안에서 cost를 정의하여 1:1 matching을 하는 작업이라고 생각하면 된다.
이를 통해 indirect set prediction에서 direct set prediction이 가능해지면서 near-duplicate problem과 같은 상황을 방지할 수 있게 된다.

$σ^{hat}$의 식에서 N은 Hyperparameter값으로 사용자가 정의해줘야하는 값이다. 이는 object class의 개수보다 더 큰 수를 assign해야하는데, 이는 dataset에 존재하는 class의 개수는 천차만별이기 때문에, "no object"의 class를 가지는 ground truth를 만들어 사용한다.

예를들어, 만약 object의 class가 3개, 그리고 N = 10이라면 3개는 class로 정의되어있지만 나머지 7개는 no class로 assign이 된다. 이를 공집합 기호(∅)로 사용한다.

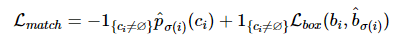
위의 match는 공집합(no object)를 제외한 class, bbox loss를 사용하게 된다.
bbox loss는 GIOU를 사용하게 되는데, 이도 간략하게 설명하겠다.
σ는 permutation을 의미한다.(앞에서 말했던 모든 case를 측정하여 가장 작은 값을 mapping하게 된다.)

GIOU(Generalized-IOU)

기존의 IOU는 단순히, $\frac{A∩B}{A∪B}$로 계산되며 알아서, normalized된 값을 이용한다(0 ~ 1의 값)

하지만, 이는 MSE, MAE를 이용하여 LOSS는 같아도 IOU값은 다른 경우가 있는데, LOSS가 크면 아무래도 직관적으로 IOU의 값이 작은 것이 일반적인데, 이러한 상황도 발생할 수 있다고 한다.

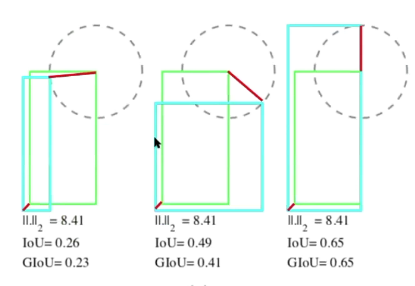위와 같은 상황이 발생.. (L2 NORM을 이용했다 했으니 이는, MSE)

어쨋든, IOU를 계산하는 좌/하단의 좌표와 우/상단의 좌표의 값을 Loss로 사용하는 것이 아닌, IOU값 자체로 Regression을 하는 것이 옳다는 것을 직관적으로 알 수 있다.(1-IOU로 regression하면 됩니다.)

하지만, Bbox의 intersection이 아깝게 생기지 않았는지, 굉장히 큰 오차로 생기지 않았는지 알 수 없기 때문에 이러한 정보를 활용하려면 또 다른 Bbox인 C를 생성하게 된다. 이러한 method가 GIOU이다.

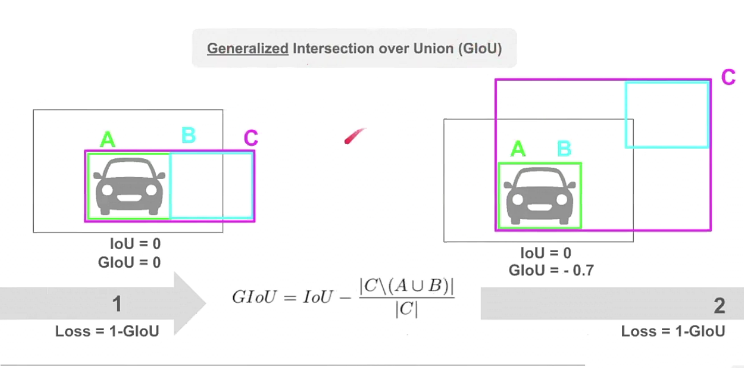
위의 그림은 GIOU를 잘 설명하는 그림인데, GIOU를 구하는 수식은 그림을 참고바란다.
A는 ground truth, B는 prediction, C는 말로 설명하기는 어려운데,, 그림에서 오른쪽과 같은 상황을 말한다.(일단 느낌을 알거라고 믿습니다.. ㅎㅎ)

어쨋든 왼쪽과 같은 상황은 A와 B가 서로 intersection된 부분은 없지만, 바로 옆에 붙어 있는 것을 볼 수 있고, C는 A와 B의 면적을 더한 값으로 볼 수 있으니 GIOU의 값은 0이 된다.

하지만, 오른쪽은 다르다. 여전히 intersection된 부분은 없지만, C의 크기는 크다는 것을 볼 수 있고 GIOU의 값은 -0.7의 값을 볼 수 있다.

그러면, A와 B가 무한대로 커지게 되면 |C \ (A∪B)|는 C로 수렴하게 된다. 수학적 수식으로는 맞지는 않지만, C - (AUB)로 직관적으로 이해 가능하다.
그래서, GIOU의 최댓값은 1, 최솟값은 -1이 되고, 최종적으로 regression을 해야하니 1-GIOU의 max값은 2, min값은 0이 된다.

---

Related Work

이 부분은 다양한 model을 간략하게 설명하고 있으니, 핵심만 전하고 넘어가겠다.

Anchor-based Methods

CLRnet은 equally-spaced 2D-Points라고 불리는 anchor를 사용하는데, 이는 NMS를 이용하는 post-processing이 필요하게 된다.
즉, duplicate prediction들을 제거하기 위해 post-processing이 필요하여 효유렁이 감소한다.
하지만, condLSTR은 fixed Lane anchor를 사용하지 않아 topology의 prediction이 뛰어나다고 한다.

Parameter-based Methods

polynomial의 order가 커지게 되면서 조그마한 error가 발생이 되어도 lane lines의 prediction은 큰 변화를 일으키게 된다.

따라서 정확도 측면에서 parameter-based는 다른 method에 비해 좋지 않다고 한다.

Segmentation-based Methods

condLaneNet은 dynamic kernel을 통해 Lane Lines를 detect하는 전체 feature map을 사용하지만, vehicle, pedestrian에 가려져 있으면 detect하기 어렵다.

또한 starting points로부터 발생된 kernel이 global info가 부족한 상태에서 만들어진다면, 이는 complex topology와 같은 lane은 다루기 쉽지 않다고 한다.