해당 글은 기본적인 Attention을 알고 있다라고 생각하고 글을 쓰겠습니다.
만약, attention에 대해서 잘 모르고 있다면 Attention의 글을 참조해주시면 좋을 것 같습니다.
이 포스트는 Transformer Paper와 Transformer Lecture를 참고 하였습니다.
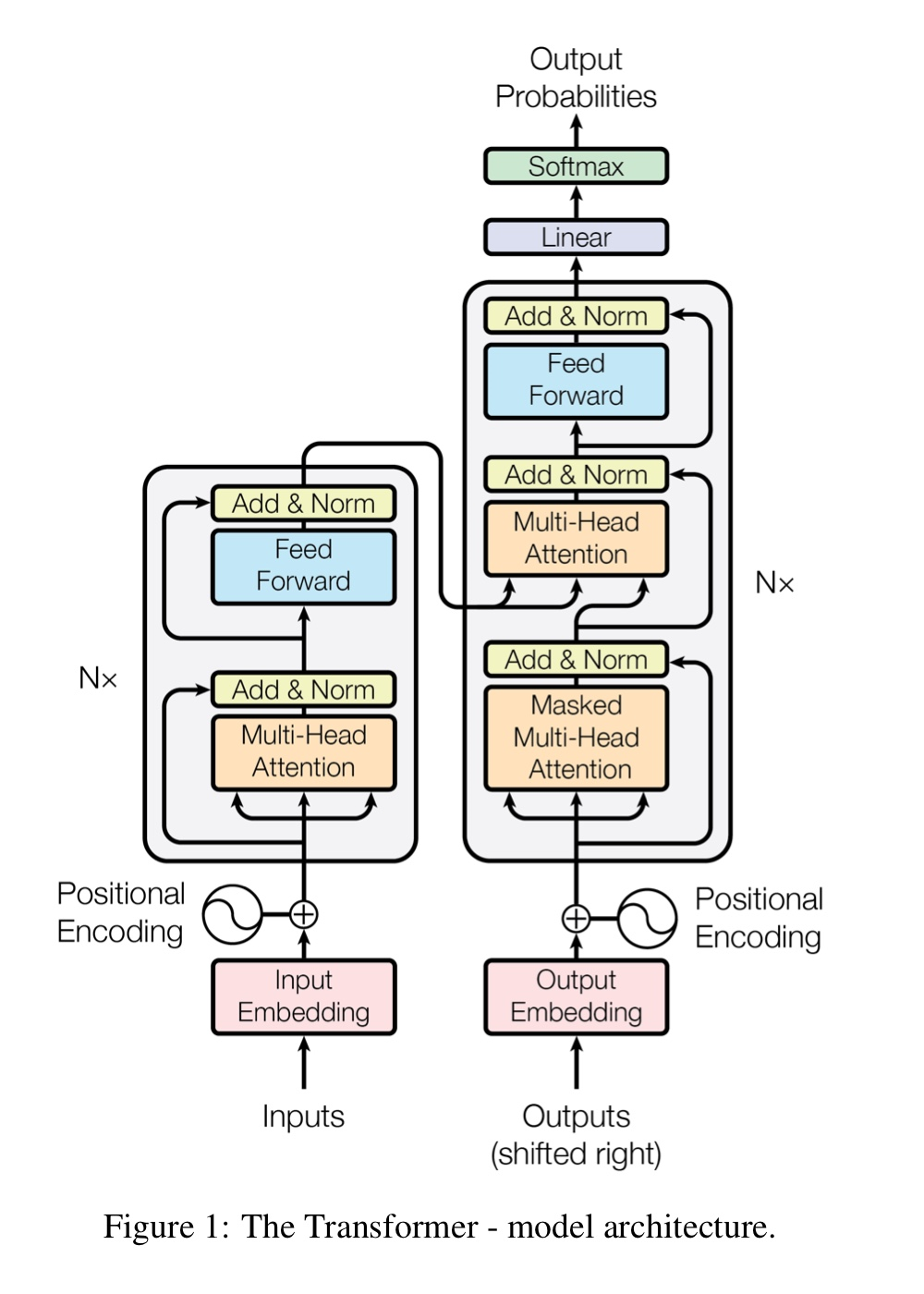
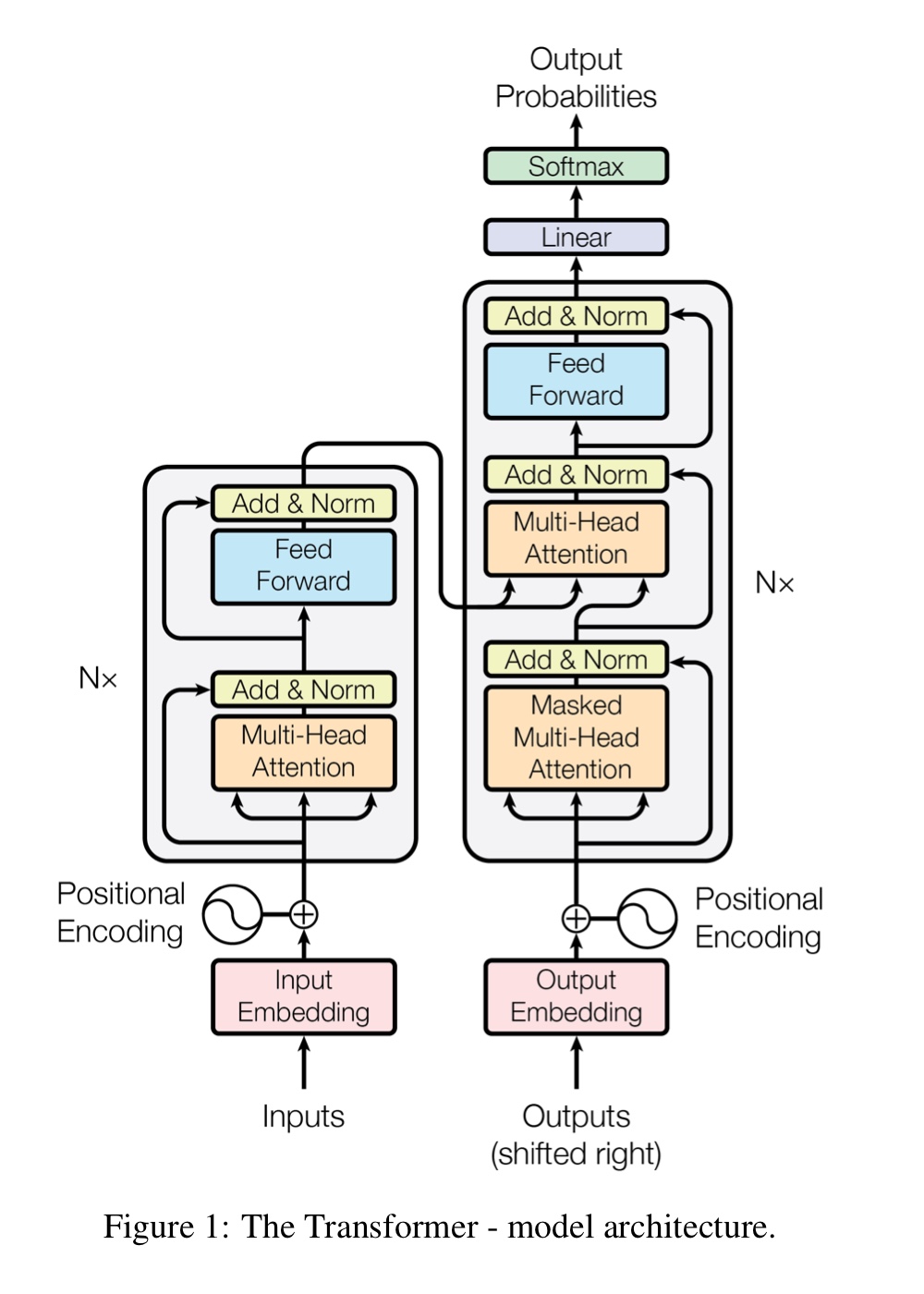
위에가 전체적인 transformer의 architecture인데, 왼쪽이 Encoder 오른쪽이 Decoder이다.
Encoder
Encoder에서 Multi-Head Attention, Add & Norm, Feed Forward, Add & norm 이렇게 4개의 sub layer개가 있으며 이 Encoder를 6번을 연달아 썼다고 한다. 즉, N = 6이라는 소리이다.
일단 Positional Encoding부분은 넘어가고 Multi-Head Attention에 대해서 다뤄보겠다.
Multi-Head Attention(Scaled Dot-Product Attention)
self-attention과 비슷한 구조를 가지고 있는데, 먼저 input embedding vector의 dimension은 512dim이다.
positional embedding vector는 + 연산을 해주기 때문에, 일단은 512dim을 가지고 있다는 것만 알아두자.
어쨋든 attention을 적용하기 전에는 512dim을 가지고 있으며, 각각의 단어에 Query, Key, Value를 구하기 위해서 의 weight matrix를 가지고 있을 것이며, 이는 weight matrix를 통과하여도 여전히 512dim을 가지고 있게 된다.
그러면 생각해볼 수 있는게, 는 512x512의 dimension을 가지고 있는 것을 알게 된다.(dimension을 아는 것이 중요하기 때문에, 자주 언급하겠다.)
어쨋든 Query, Key, Value를 구했지만 여기서 끝이아니고 논문에서 표현한 "Linear Projection"이라는 표현을 썼는데, weight matrix를 또 다시 정의하여 dot product를 수행한다.
그니까, Query, Key, Value 구하고 또 다시 weight matrix를 곱해주게 되는 것이다.
이때 weight의 matrix의 dimension은 512x64로 각각의 output matrix의 dimension은 64가 되게 된다.
그러면 최종 Attention Score의 dimension은 64가 되는 것을 알 수 있다.
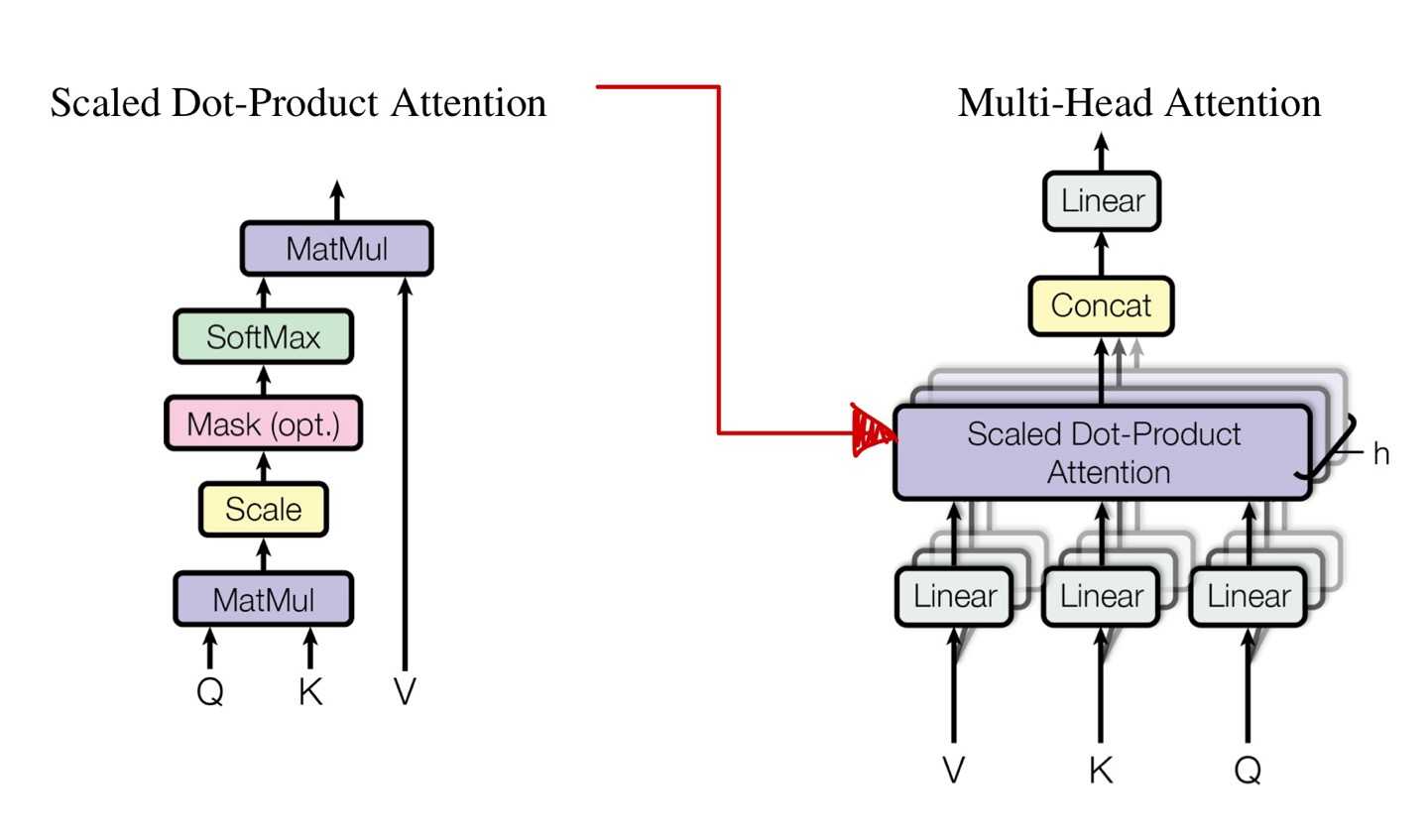
위 구조에서 Mask는 Decoder에서만 사용하기 때문에 (opt.)이라는 표현이 있는 것이다.
어쨋든, 위는 attention score를 구하기 위한 과정이다.
앞서, 다른점을 언급했을때 "Scale"부분을 이야기하였는데 이는 그냥 로 normalization을 해주었다고 보면 된다.
가 아닌, 또는 로 나누어주어도 상관없다. 왜냐하면 dimension이 같기 때문이다.
조금 더 자세히 살펴보자면, Scaled Dot-Product Attention에서 Q, K, V는 모두 dimension이 64이고, 최종적인 attention score의 dimension도 64가 된다.
여기서 는 Key dimension의 square root를 의미하며, 의 값이 64이기 때문에 = 8이 되는 것을 알 수 있다.
왜 이러한 normalization을 해주는 것일까?
이는, dot-product 과정에서 큰 값은 너무 큰 값을 가지게 되는 것을 방지해주고자 scale과정을 넣었다고 한다.

먼저 MultiHead(Q,K,V)를 보기 전에 각각의 matrix가 무엇을 뜻하는지 앞에서도 봤지만, 다시한번 보고 넘아가자
를 보게되면, 처럼 각각 Key, Value도 마찬가지로 되어있는데 이는 Linear Project의 과정을 포함하는 것이다.
이에 대한 output을 로 표현한 것이며, 이는 h=8개로 8번을 적용했다라는 의미가 된다.
은 Linear Projection전의 Query, Key, Value의 dimension을 나타내므로 512가 된다.
어쨋든 마다 dimension은 64가 되고, 이를 8번을 적용하여 각각의 결과값을 concatenate하게 되니, 의 dimension은 512가 된다.
이 concat값에 또 다시 Linear Projection을 하여, weight matrix인 를 dot product를 해주게 되는데 의 dimension은 512x512이다.
뭐 어쨋든, 이를 다시 를 곱하여 512로 dimension을 늘렸으니 bottle neck의 구조를 사용한 것으로 생각된다.
이렇게 여러개의 Multi-Head Attention을 사용한 이유는 주목해야 하는 다른 단어가 무엇인지를 더 잘 파악할 수 있으며, 각 단어가 갖고 있는 문맥적 특성을 더 잘표현한다고 한다.
Add & Norm
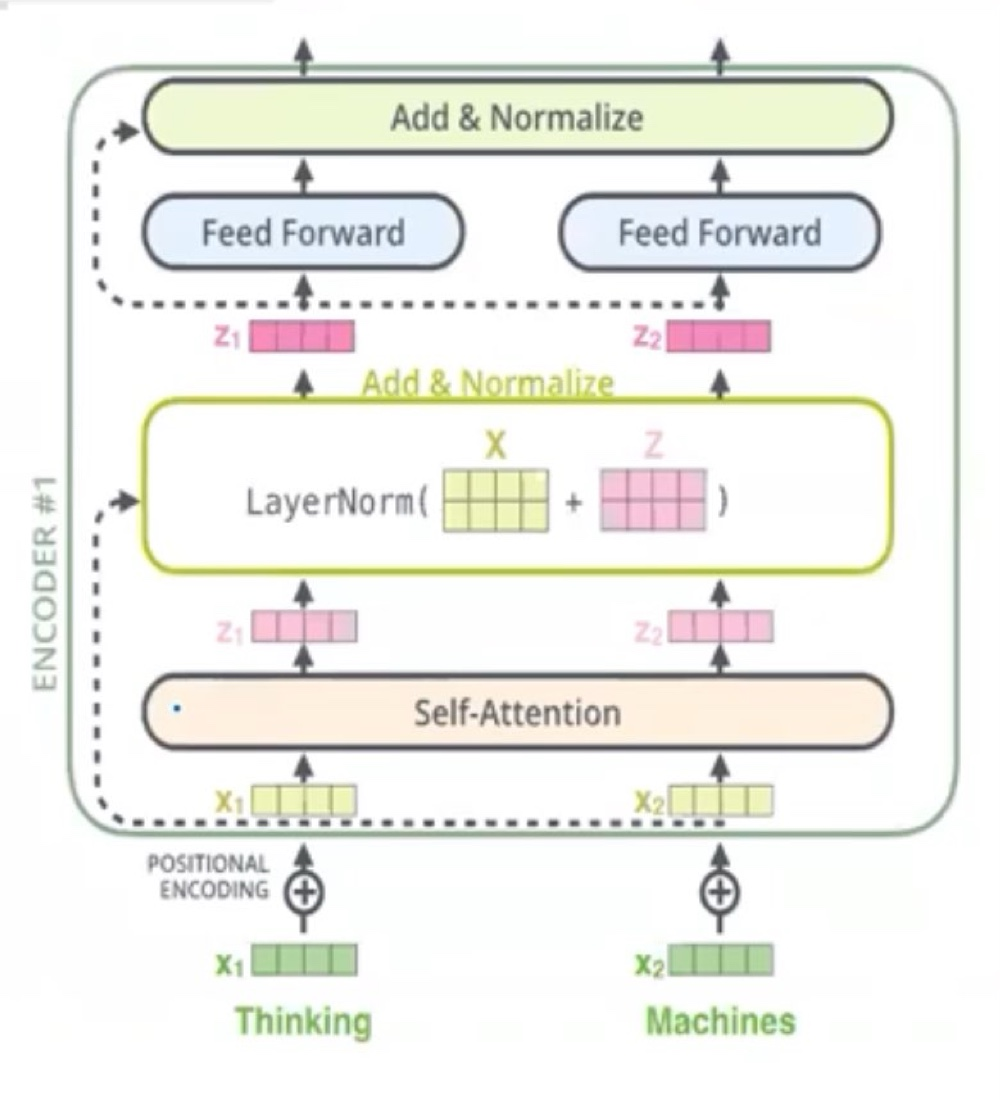
이 부분은 positional embedding을 적용하고 난 뒤의 X값에 self-attention을 적용하고 난 뒤의 output인 Z를 구한 모습이다.
이후, 이 값을 ResNet에서 사용하는 skip-connection과 유사하게 X와 Z의 값을 더하여 attention score의 값을 X에 넣어주고, 그 값을 LayerNormalization을 하게 된다.
Layer Normalization
Layer Normalization의 수식은 가 된다.
γ 앞의 수식은 z-score로 표준정규분포로 변경해주는 수식이며 평균이 0, 표준편차가 1로 설정되게끔하여 정규화를 시켜주는 수식이며, γ과 β는 학습할 수 있는 parameter로 weight의 값을 가진다.
γ는 scaling의 역할, β는 shift의 역할을 한다.
이는 Mini-batch의 instance별로 평균값을 빼주고, 표준편차 값으로 나누어주게 되며, 혹시나 분모가 0이 되는 것을 방지하기 위해 임의의 ε값을 설정해주게 된다.
Position-wise feed-foward network
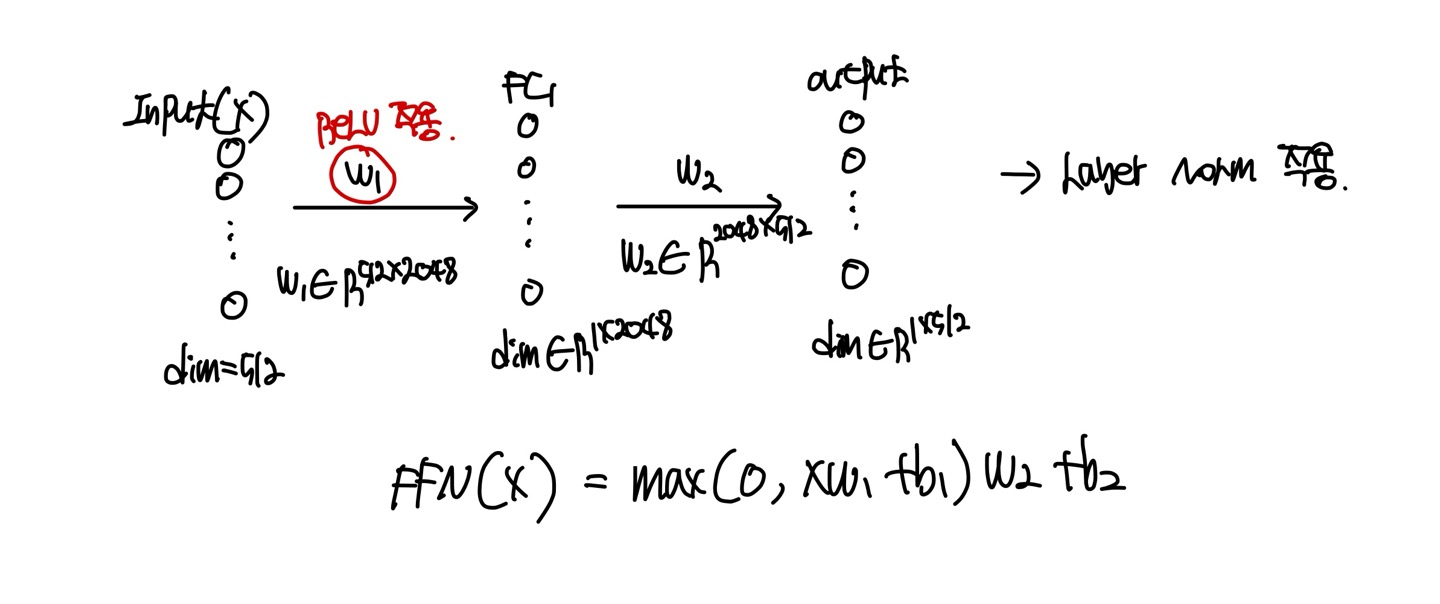
Layer Norm 설명은 여기서 마치고, Layer Norm의 결과값을 또 다시 Feed Foward라는 method에 넣어주게 되는데, 이는 그냥 MLP이다.
Position이라는 단어가 있는데, 이는 각각의 단어별로 서로 다른 feed foward가 적용이 되었다고 보면 된다.(Token마다 독립적으로 적용한다.)
로 표현되며, 마지막 layer를 적용할때는 ReLU activation function을 쓰지 않은 것을 볼 수 있다.
이때, 는 단어가 변하여도 값이 다르지 않고 동일한 를 이용하게 된다. 이를 weight sharing이라고 한다.
이 Feed Foward의 output에 다시 Add & Norm을 적용해주고 이를 1번 적용했으니 5번을 적용을 더 해야하니, 첫번째의 output이 두번째의 input으로 들어가게 된다.
Decoder
Encoder부분에서 살펴보지 않은, Positional Embedding에 대해서 살펴보자
Positional Embedding
Transformer에서는 단어들간의 embedding정보만을 사용하는 것이 아니라, 입력된 sequence data내의 position(위치)정보도 사용한다.
이러한 이유는 RNN이나 LSTM과 같은 순환신경망 구조를 사용하지 않고 attention만을 사용하기 때문이다.
따라서, 이러한 이유로 Positional Embedding을 쓰게 된다.
Positional Embedding에서는 학습시킬 수 있는 가중치가 따로 존재하지 않으며, 공식에 넣어 위치정보를 알 수 있다.
단어의 vector가 이고 Positional Embedding이 이라면, 단어의 vector과 Positional Embedding을 단순히 mapping되게 더해주기만 하면 최종 위치정보를 포함한 embedding된 vector가 나오게 된다.
공식은 다음과 같다.
, j가 짝수인 경우
, j가 홀수인 경우
i와 j가 의미하는 것은 에서 단어 i의 positional embedding vector의 위치 j의 원소값을 의미한다.
예를들어 ['Today', 'is', 'Friday']라는 input token이 있고, embedding dimension이 512라고 가정해보자.
먼저 Today의 PE를 먼저 구해보면, index가 0이기 때문에 i = 0이다.
따라서, 이 된다.
그렇다면 'Friday'는 index가 2이므로 i = 2이다.
따라서, 이 된다.
embedding vector가 512이므로, 나머지도 위와 같이 계산되며 PE의 dimension도 512가 되겠다.
어쨋든 위에서는 token마다 각각 구해줬지만, matrix를 통해서 한번에 구할 수 있다는 것도 잊지말자.
Masked self-attention
Encoder의 self-attention과 다르게 작동하게 되는데, Masked self-attention은 학습(training)단계에서 teacher forcing을 이용했다.
Teacher Forcing
Decoder는 Language model의 역할을 하기 때문에, 학습 단계에서 현재 단계까지 예측한 단어들의 정보를 사용하여 다음 단어를 예측하는 것이 아닌, 정답(target) 정보만을 이용해서 각 단계의 단어들을 예측하게 된다.
왜냐하면, 예측한 단어들의 정보를 이용해서 다음 단어를 예측하는 경우(language model에 대한 설명)에는 이전 단어들에 대한 예측이 잘못되면 그 다음 단어를 예측이 제대로 될 수 없기 때문이다. 그렇기 때문에 다음 단어를 잘못 예측하여도, 학습 과정에서는 target 정보만을 사용하는 것이 된다.
따라서 attention score를 구하는 과정에서도 다음 단어를 예측해야하니, [<sos>, 'Today', 'is', 'Friday']에서 'is'를 예측하는 경우에는 'is'전까지의 query, key, value를 통해 attention score를 구하면 되겠다.
어떻게 이러한 과정이 진행되냐면, 마지막 softmax함수를 써주게 될때, -∞ 값만을 넣어주게 되면 softmax의 분자가 0이 되게 된다.(분모는 전의 값까지 합쳐주기 때문에 0이 될 일이 없음, 따라서 발산하지 않음), 이러한 과정으로 예측 전의 단어들을 무시할 수 있게 된다.
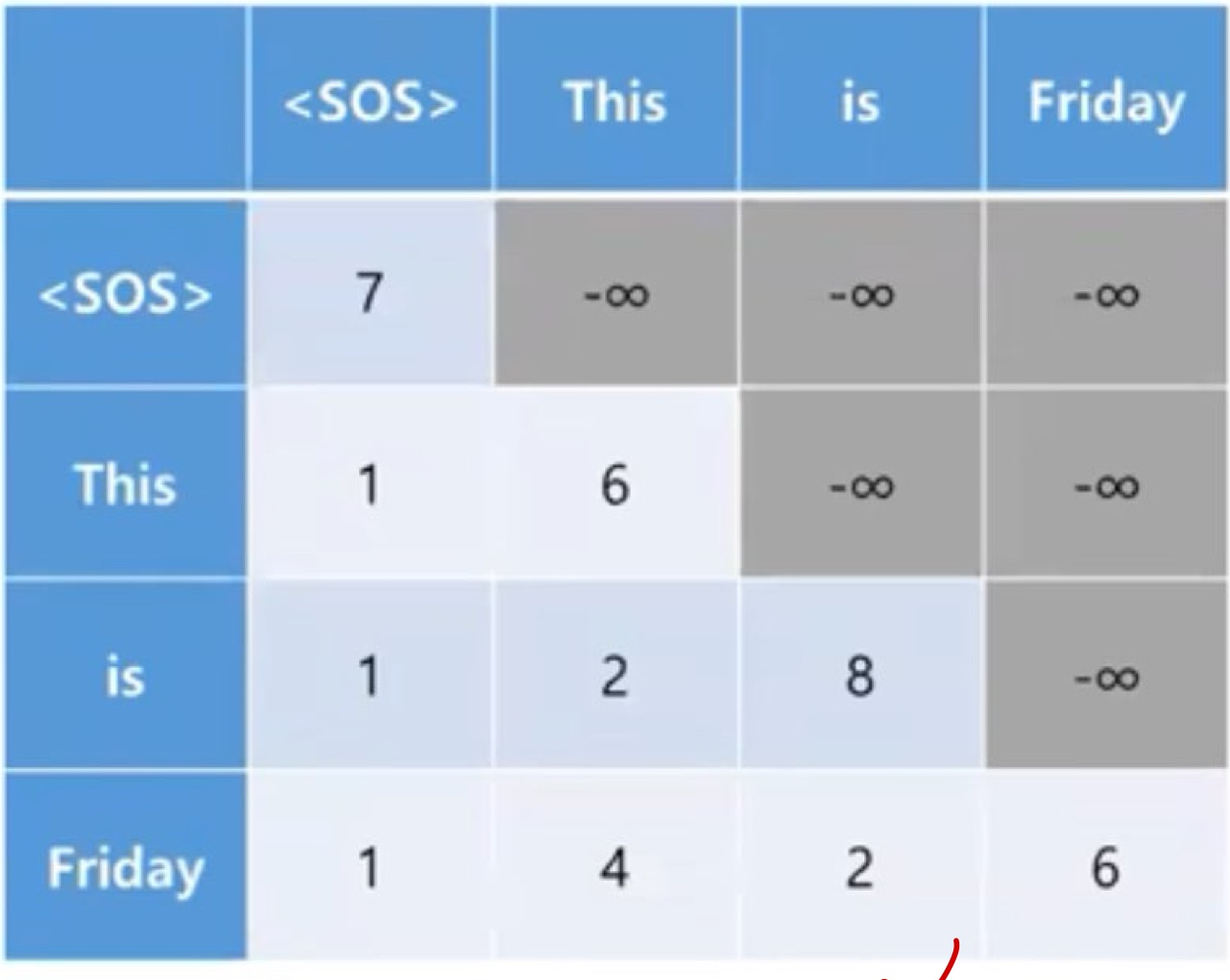 그래서 위의 -∞가 채워져 있는 것을 masking 작업이라고 하여, Masked Multi-Head Attention이라고 불리운다.
그래서 위의 -∞가 채워져 있는 것을 masking 작업이라고 하여, Masked Multi-Head Attention이라고 불리운다.
Multi-Head Attention
맨 위의 도식화된 architecture를 보게 되면, 이 부분은 Encoder의 최종 output을 사용하는 attention이다. (Encoder의 정보를 사용했다는 것이 중요)
self-attention과 마찬가지로 query, key, value vector들을 사용하며 query는 decoder 부분에 입력된 token에 대한 query를 사용하며, key와 value는 encoder에서 각 token에 대한 값으로 전달된다.
나머지 부분은 Encoder에서 설명한 self-attention과 동일하다.
Decoder안에서의 Add&Norm 부분은 Encoder와 똑같으므로 설명은 생략했으며, 위의 Decoder의 작동은 논문에서 6번 진행된다고 한다. (Encoder에서는 6번)
Decoder의 최종 output은 Linear로 input으로 들어가게 되는데, 이는 Fully Connected Layer를 의미하며, 각각의 단어들에 대한 확률값을 계산해야하기 때문에 softmax를 이용하여 최종적인 단어들에 대한 확률 값이 나오게 된다.
