Infrared and Visible Image Fusion using a Deep Learning Framework

홍성민·2024년 11월 5일

논문 리뷰

목록 보기

16/16

Abstract

Image style transfer이란, 특정 style을 가진 이미지를 다른 이미지의 content에 적용하여 새로운 이미지로 만드는 기술을 의미하는데 이미지의 시각적 style 예를들어 색감, 질감 등과 같은 것들을 추출하고 이를 구조적 정보 예를들어, 형태, 구조 등에 결합하는 과정이다.

image style transfer에서 feature를 extraction할 때, VGG-Network를 많이 사용한다.

따라서, image fusion에서는 두 이미지를 결합하여 content 이미지의 형태를 유지하면서 style 이미지의 시각적 특성을 반영한 새로운 이미지를 만드는 것이다.

image fusion에서도 Deep Learning이 좋은 achievemenet를 거두었다는 논문으로, architecture에 대한 글 입니다.

Framework

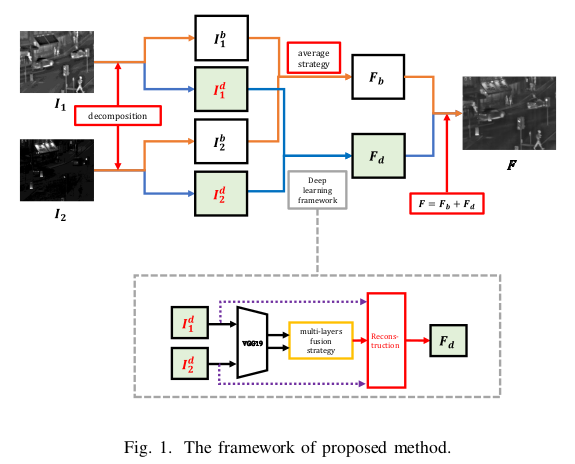
이 Architecture는 base part와 detail content로 구성되어 있습니다.

Fig. 1.을 보면 source images가 $I_1, I_2$ 가 있는데 이는 visible, infrared image로 볼 수 있다. 논문에서는 K pregistered source images라고 표현했는데, K=2로 설정했다고 한다.

Base Parts

base part는 이미지에서 저주파 성분으로, 주로 이미지의 전반적인 구조, 색상, 밝기와 같은 정보를 포함한다.
우리는 먼저, 해당 architecture를 사용하기 위해서는 base part를 optimization을 해야하는데 수식은 다음과 같다.

$I_k^b=argmin_{I_k^b}||I_k-I_k^b||^2_F+λ(||g_x*I^b_k||^2_F+||g_y*I^b_k||^2_F)$

수식을 하나하나 살펴보자

$||I_k-I_k^b||^2_F$ 에서 F는 Frobenius norm을 의미하는데, $||A||_F = \sqrt{\sum_{i=1}^m \sum_{j=1}^n |a_{ij}|^2}$ 이다.
이는, 2개 이상의 이미지의 pixel값들이 차이를 계산할 때 사용하고, 이미지의 유사성을 측정하는 지표이다.

$I_k=\begin{bmatrix}1&2&3\\4&5&6\\7&8&9 \end{bmatrix}$ 의 source image와 $I_k^b=\begin{bmatrix}1&2&2\\3&5&6\\7&7&9 \end{bmatrix}$ 의 base part가 있다고 해보자.

$I_k-I_k^b = \begin{bmatrix}0&0&1\\1&0&0\\0&1&0 \end{bmatrix}$ 이 되고 norm을 구하게 되면 $1^2+1^2+1^2$ 으로 3의 값이 나온다. (0은 생략)

따라서 image fusion을 하는데, content는 유지해야하니 해당 값이 차이가 나면 안되기 때문에 optimization수식 값에 넣어준 것입니다.

$||g_x*I^b_k||^2_F$ 와 $||g_y*I^b_k||^2_F$ 는 각각 horizontal, vertical edge를 detect하기 위한 kernel로 $g_x = [1, -1], g_y = [1,-1]^T$ 이다.

$g_x$ 가 horizontal, $g_y$ 가 vertical edge filter이다.

이미지에서 미세한 detailed, edge, texture와 같은 정보들을 고주파 성분이라고 하는데, 이는 이미지의 선명함과 해상도를 높여주는 역할을 한다.

따라서, Base Part는 이미지에서 저주파 성분만을 가지고 있으므로 고주파 성분의 값을 최소화하는 optimization function을 구성한 것이다. (λ=5로 설정하였다고 합니다.)

Detailed Content

바로 위에서 Base Part부분의 optimization problem을 해결하고 난 뒤 detailed content를 얻을 수 있는데, base part는 저주파 성분들로만 이루어져 있는 것이니 단순히 $I_k^d=I-I^b_k$ 로 고주파 성분의 이미지를 얻을 수 있다.

Fusion of base parts

$I_k^b$ 가 $\{I_1, I_2\}$ 에서 얻어져도 redundant information이 존재할 수 밖에 없다.
따라서, 이를 parameter값으로 visible, infrared의 정보를 포함하게 되는데 논문에서는 To preserve common feature and reduce redundant information으로 표현되어진다.

Image fusion에서 Common feature란 2개 이상의 이미지에서 의미 있는 정보를 공유하는 부분이며 Redundant information은 여러 이미지에서 동일하거나 거의 동일한 정보이지만 그 자체로 추가적인 가치를 제공하지 않는 것 입니다.

$F_b(x,y) = α_1I_1^b(x,y)+α_2I_2^b(x,y)$
visible과 infrared image에서 각각 얻는 base part의 fusion은 위의 식으로 나타낼 수 있다.

$(x,y)$ 는 pixel coordinate
$α_1, α_2$ 는 weight value로 0.5의 값을 가진다.
$I_1^b(x, y)$ 는 visible image의 저주파 성분 pixel value
$I_2^b(x, y)$ 는 infrared image의 저주파 성분 pixel value

여기서 가지는 한계점은, $α_1$ 과 $α_2$ 를 같게해준 것이 한계점인 것 같다. 서로 다른 domain의 weight를 동시에 주었기 때문이다.

Detail Content

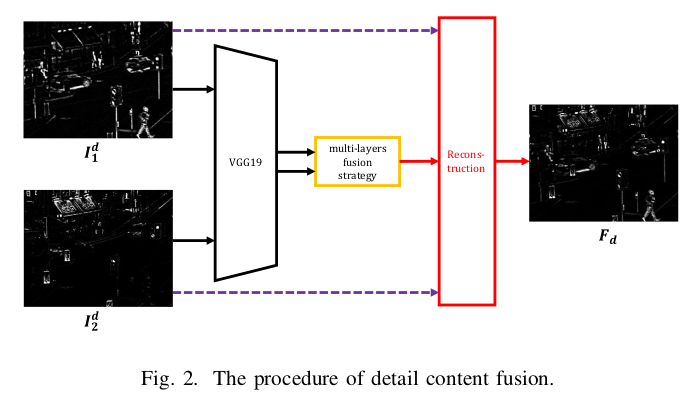
$\{I_1^d, I_2^d\}$ 는 $I_k-I_k^b$ 로 각각의 domain에 맞는 저주파 성분을 빼, 고주파 성분만이 남은 값들이다.
따라서 위의 사진을 보면, 고주파 성분인 구조, 패턴, edge 등이 있는 것이 보인다.

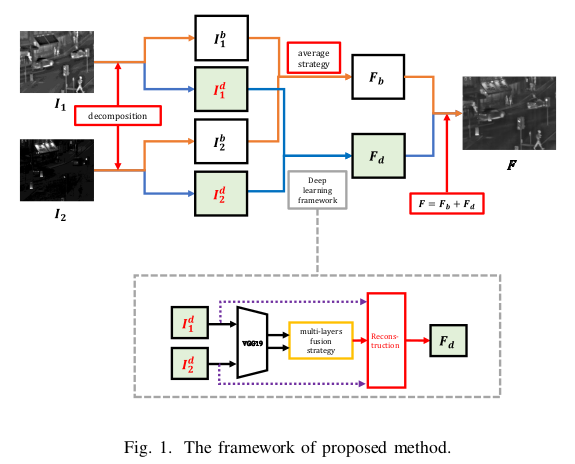
전체적인 PipeLine은 다음과 같다.
1. Extract Deep features to VGG19
2. Multi-layers fusion strategy를 통해 weight map을 만든다.
3. weights map과 detail content로 reconstruction한다.

Multi-Layers fusion strategy

$φ_k^{i,m}=Φ_i(I_k^d)$

$I_k^d$ : Detail Cotent(고주파 성분 이미지)
$φ_k^{i,m}$
- k: k번째 detail content
- i: i번째 layer
- m: i번째 layer에서 channel number
- VGG Network의 각 Layer $φ_i$ 를 통과시켜 얻은 feature map이다. 이때 $i$ 는 $i∈\{1,2,3,4\}$ 로 1,2,3,4의 layer를 의미한다.

따라서 $φ_k^{i, 1:M}(x,y)$ 는 특정 layer i에서 (x,y)위치의 모든 feature값들을 모아 만든 vector이다. 따라서 M은 특정 layer의 i에서 얻어진 feature map의 개수를 의미하며 M-dimensional vector가 된다.

예를들어 $relu_{11}$ 의 layer에서 64개의 feature map이 있다고 하고 해당 layer를 통과한 output이 $224(height)*224(width)*64(channel Number)$ 라고 하고 특정 pixel위치 (150, 200)에서의 64개의 feature map을 1개씩 추출하면 64-dimensional-vector가 되게 된다.

즉, $φ_k^{1:1:64}(150,200)=[0.2, 0.5, ..., 0.1]∈R^{1*64}$ 가 되는 셈이다.

이 과정을 각 $(x,y)$ 에 대해 반복하면 모든 위치 $(x,y)$ 에 대해 대응되는 형태의 tensor가 된다.

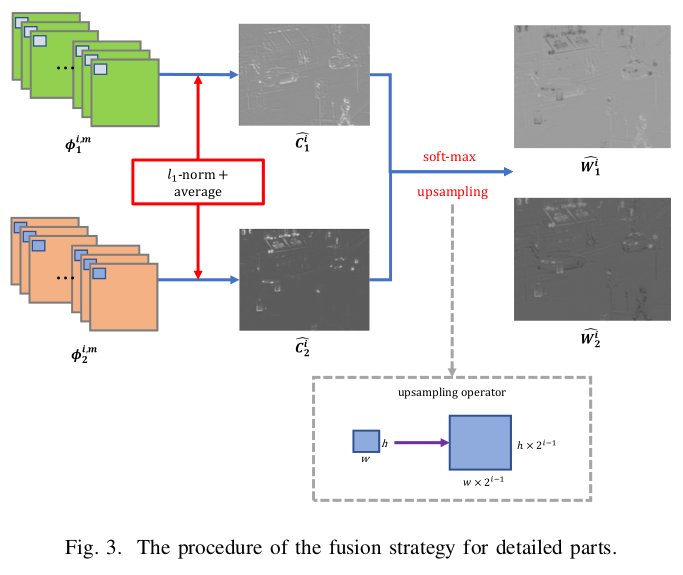
$||φ_k^{i,i:M}(x,y)||_1$ 은 source detail content의 activity level measure가 된다.
이는 $C_k^i(x,y)=||φ_k^{i,i:M}(x,y)||_1=\displaystyle\sum_{m=1}^{M}{|φ_{i,m}^k(x,y)|}$ 이며, block-based average operator를 사용하여 final activity level map인 $\hat{C}^i_k$ 를 구하는데 이는 misintegration을 robust하게 만들기 위함이다.

misintegration이란, 2개의 source image가 완벽하게 정렬되지 않은 경우로 여러 image를 겹쳐서 처리할 때, 각 image의 위치, 크기, 방향, 변형 등이 정확하게 일치하지 않은 경우를 의미한다. 이는 image fusion단계에서 흔히 발생하는 오류로 카메라의 움직임, 물체의 움직임(시간차를 두고 움직임), 렌즈 왜곡 등으로 발생한다.

$\hat{C}^i_k=\frac{\sum_{β=-r}^{r}\sum_{θ=-r}^{r}c^i_k(x+β, y+θ)}{(2r+1)^2}$ 로 final activity level map을 구성하며 r은 block size(kerenl size)를 의미한다. r이 커지면 misintegration이 robust하지만 detail은 잃게 됨으로써 저자는 1을 사용했다고 한다.

weights map을 구하기위해서 각 source image의 activity map을 이용하여 softmax-function을 이용하게 되는데 수식은 다음과 같다.

$W_k^i(x,y)=\frac{\hat{C}^i_k(x,y)}{\sum_{n=1}^K\hat{C}^i_k(x,y)}$ , 이는 각 source image의 i번째 weights map을 의미한다.

논문에서, VGG의 pooling operator를 언급하는데 이는 maxPooling operator를 의미한다. pooling이 $\frac{1}{s}$ 만큼 작아지게 되므로 s는 stride를 의미하며 각 layer마다 $\frac{1}{2^{i-1}}$ 배 feature map이 input대비 줄어들게 된다.

Final weight map

$W_k^i$ 를 얻고 난 뒤, $W_k^i$ 를 detail content의 input 크기와 똑같이 resize를 해주게 되는데, 이는 upsampling operator를 의미한다.
resize의 output이 $\hat{w}_k^i$ 이며, 이는 $I_k^d$ 와 똑같은 size이다.

수식은 다음과 같다.
$\hat{w}_k^i(x+p,y+q)=W_k^i(x,y), [p,q∈\{0,1,...,(2^{i-1}-1)\}$

이는, $W_k^i$ 를 upsampling하여, 최종 $\hat{w}_k^i$ 를 생성한다. 이는 최근접 이웃 보간법으로 "Nearest-Neighbor Interpolation"이라고 하는 upsampling 기법이다.
또한, $p,q$ 는 pixel값을 확장 할 범위를 나타내며, $2^{i-1}$ 은 해상도 증가를 나타내고, 각 pixel값이 복사될 크기를 정의한다.