Abstract

ResNet은 residual learning을 통해서 이전에 사용했던 layer들보다 모델의 구조를 deep하게 layer를 구성할 수 있으며, 이는 모델의 각 layer마다 input값을 참조함으로써 가능하다고 한다.

Residual learning의 장점은 다음과 같다.

• Easier to optimize

• Increased depth를 통해서 more gain accuracy

• Lowe Complexity than VGG(이때의 ResNet은 152layers를 구성했다고 한다.)

ImageNet, CIFAR-10, COCO 등의 dataset를 통해서 residual learning이 generic한 것을 증명했다고 하며 ILSVRC 2015 Classification task에서 1등을 차지하였다고 한다.

---

Introduction

Network는 여러 layer들로 구성되어 있으며, 자연스럽게 low/middle/high-Level 수준의 feature와 classifier를 종단 간에 다층 구조로 통합하고 있기 때문에 feature의 level은 layer의 depth에 따라 풍부해진다고 한다.(성능이 더 좋아진다는 의미)
이는 layer의 depth가 매우 중요하다는 서사이다.

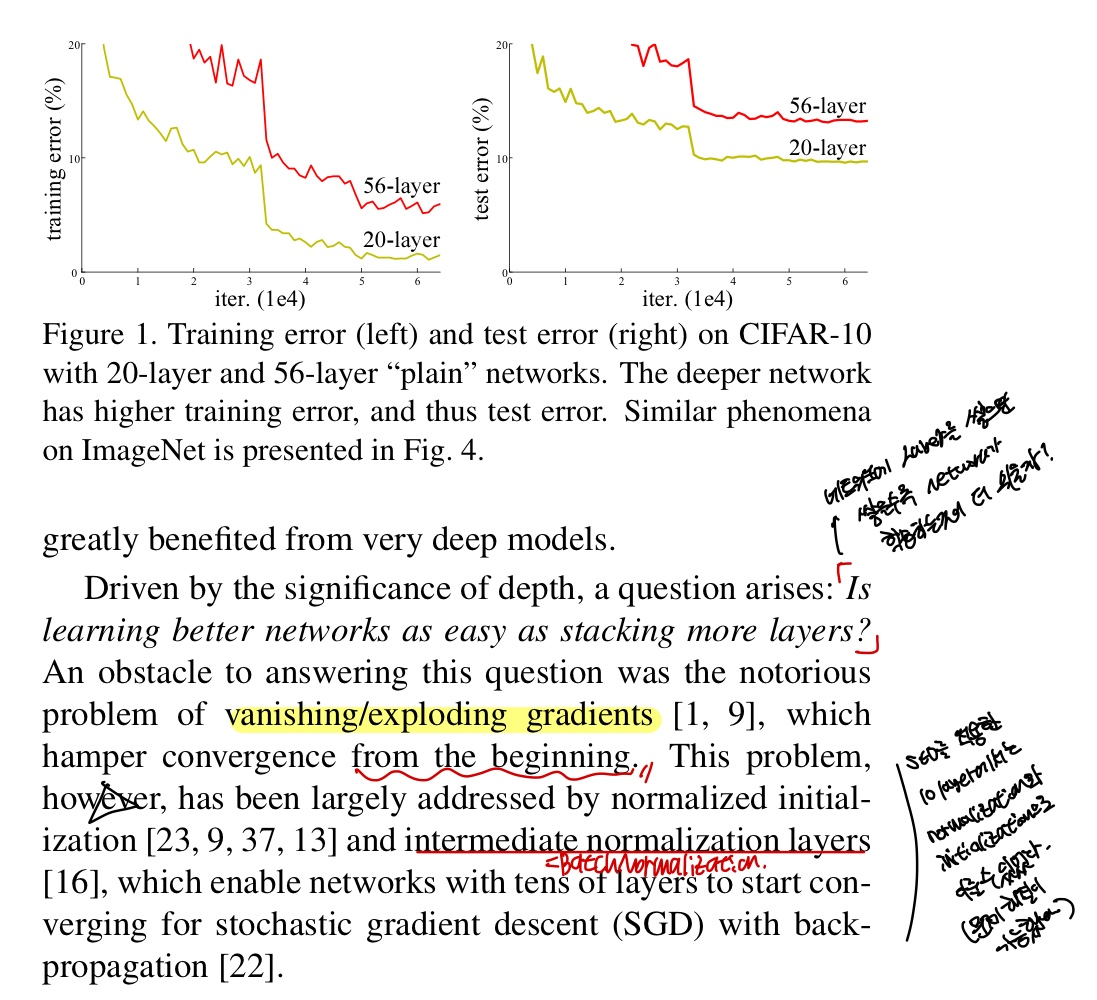
Figure 1.을 보게되면, 20,56-layer의 plain network로 CIFAR-10을 학습한 iter에 따른 error의 변화량을 나타냈다.
위에서 depth의 중요도를 말한 것과는 달리 56-layer가 20-layer보다 error가 크다는 것을 보여준다.

논문에서도 다음과 같은 의문점을 제기한다
"Is learning better networks as easy as stacking more layers? 이 뜻은 더 많은 layer를 쌓는 것만으로 network가 학습하는 것이 더 쉬운가? 라는 질문으로 이 말을 한 의도는 그렇지 않다는 것을 의미하며 이에 대한 obstacle로는 gradient vanishing을 원인으로 보았다고 한다.

gradient vanishing에 대한 solution은 normalized initialization(He init)과 BN과 같은 intermediate normalization으로 해결할 수 있었다고 한다.

여기서부터 설명이 어려우니 천천히 따라오길 바랍니다.

Figure 1을 보면 more deep한 network가 converging 하려할때 degradation의 문제가 발생한다고 합니다. 이는 overfitting의 문제가 아니고 적절하게 깊은 network에 더 많은 layer를 추가하면 training error가 커진다는 것을 실험으로 확인하였다고 합니다.

이 논문에서는 degradation의 문제를 "Residual Learning"으로 해결하였다고 합니다.

Figure 2가 residual learning의 아키텍처이며 x(layer의 input값)을 output값에 더해줌으로써 gradient vanishing의 문제를 해결할 수 있게 됩니다.

왜 그런지 이제 설명해보겠습니다.

먼저 H(x)를 우리가 바라는 이상적인 값, 논문에서는 desired underlying mapping이라고 언급하고 있네요. 우리가 바라는 이상적인 값이란 layer를 통과하고 난 후의 output값과 input값의 차이가 별로 크지 않는 값을 말합니다.

수식은 H(x) = F(x) + x로 x는 단순히 입력값으로 constant의 값이므로 F(x) = H(x) - x를 학습을 하기만 하면 되고 F(x)가 0으로 되게끔 학습하게 됩니다. 즉, H(x) = x가 되게끔 학습을 하게 되겠죠?

왜냐하면, 이것은 미리 이상적인 값 H(x)에 x를 더해주는 즉, 미리 prior를 주었기 때문에 F(x)의 학습이 더 쉬워지게 됩니다. 왜 F(x) = 0이 되도록 하는 것이 최적의 해인 이유는 layer마다 output값이 variance가 심하게 되면 이는 overfitting이 일어난 것임을 알 수 있습니다. 그렇기 때문에 H(x) = x로 되게끔 학습을 진행해 나가야 하며, network는 값을 조금씩 바꿔 나가는 것이 안정적인 모델이라고 할 수 있습니다.

논문에는 나와있지 않지만, 어떻게 gradient vanishing의 현상을 막을 수 있는지 수식으로 나타내겠습니다.

이로 인해 gradient가 더 직접적으로 흐르게 되고, 중간에 발생하는 gradient vanishing 현상이 줄어들게 됩니다. 그 결과, network를 훨씬 더 깊게 학습시킬 수 있는 효과를 가져옵니다. skip-connection은 이러한 방식으로 gradient의 흐름을 보다 원활하게 만들어 network의 학습을 돕는 역할을 합니다.

이러한 identity mapping은 추가적인 parameter를 필요로 하지 않으므로 더 많은 computational complexity를 요구하지도 않습니다.
전체 layer들은 SGD를 통한 backpropagation을 통해 end-to-end 학습이 가능해졌다고 말합니다.

plain network와 residual learning network를 비교를 나타내고 있으며 당연히 residual learning network가 성능이 더 좋았다고 말하고 있습니다.
모델이 1000개의 layer를 추출하는 것도 성공했다고 말하며 Ensemble을 통해 3.57의 error를 낮추었다고 하며, 다른 recognition task에도 performance가 generalization을 확인하였다고 합니다.

---

Related Work

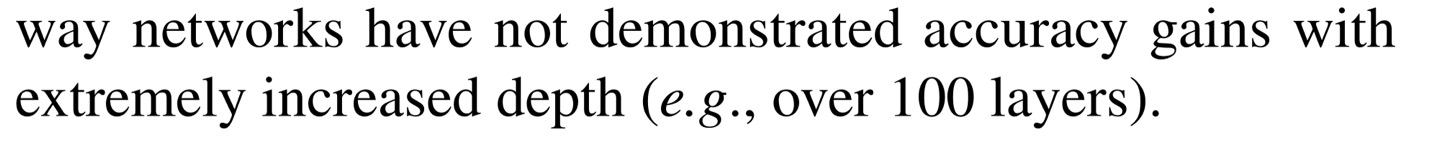
Shortcut은 많은 연구와 이론을 통해서 오랜 기간 연구되어 왔으며 MLP에 Linear layer를 추가한다던지, 중간 layer의 gradient vanishing을 막기 위해서 auxiliary classifier(보조 분류기)를 연결하든지 등 다양한 연구들이 이루어져 왔다고 합니다.

Identity mapping을 통한 shortcut은 parameter-free(parameter를 요구하지 않음)과 never-closed(gradient가 0으로 수렴할 일이 없음)으로 모든 information이 항상 통과된다고 합니다.

---

Deep Residual Learning

Residual Learning

Introduction에서 residual learning에 대한 설명을 다 했기 때문에 여기서는 추가적으로 설명할 것이 없습니다.

Identity Mapping by Shortcuts

모든 Building Block(Figure 2)에 Residual Learning을 adopt하였다고 하며, 이를 수식으로 나타내면, Eqn(1)과 같다.
이때 y는 H(x), $F(x, {W_i})$는 F(x), x는 identity이다.

Figure 2에서의 building block은 layer가 2개가 있으며 σ는 ReLU를 뜻한다.

+는 F(x)와 x의 dimension이 맞아야하며 element-wise addition operation을 수행한다고 한다.(kernel일때는 channel by channel로 operation 수행)
만약 F(x)와 x의 dimension이 맞지 않을때에 x에 $W_s$를 multiply해줌으로써 dimension을 맞춘다고 한다.(1x1 conv 등등) $W_s$는 단순히 dimension을 맞추는 것에만 관여하며 ,degradation의 문제를 해결하는데는 identitiy mapping만으로 충분하다고 설명합니다.

Eqn(1)에서 no more param/complexity라는 것을 강조하며 plain network와 비교할때 실제로 무시할 정도로 작은 operaiton인 element-wise addition을 제외하면 computational-complexity가 비슷하다고 하였다.

또한 논문에서는 building block에 layer가 2~3개밖에 없는데, 추가적인 layer를 구성하여도된다고 하며, 다만 layer가 1개인 경우에는 linear layer와 비슷하다고 합니다.(y = $W_1 x$ + x)

Network Architectures

Consistent Phenomena를 발견했다고 하며, 이를 설명하기 위해 ImageNet을 위한 2가지 model을 설명합니다

Plain Network

Plain의 baseline model은 VGG로 영감을 받았으며 conv filter는 3x3이고 2가지의 규칙을 따랐다고 합니다.

1. Output feature map의 size가 같다면, layer들은 똑같은 filter수를 갖는다. 즉, MaxPooling을 하기전에는 똑같은 filter의 개수를 적용한다는 뜻이다.

2. Output feature map의 size가 반으로 줄어 시(MaxPooling 적용 후) 각 layer의 time-complexity를 유지하기 위해 filter 개수를 2배 늘려줍니다.

network의 마지막 부분은 GAB(Global Averaging Pooling)을 구성하고 1000개의 class를 classification하기 위해서 softmax를 쓴다고 합니다.

이렇게 Plain Network를 구성함으로써 VGG-19의 FLOPs의 18%밖에 안되는 FLOPs를 차지한다고 합니다. Plain Network는 3.6billions, VGG-19는 19.6billions

Residual Network

앞선 Plain Network에서 shortcut connection만을 추가해주었다고 하며 Solid line(실선)에서는 input과 output의 dimension이 맞는 것, Dotted line(점선)에서는 dimension이 증가할 때를 나타냅니다. 여기서의 dimension이 증가한다는 것은 feature map의 크기가 커진다는 것을 의미합니다.

Dotted line일때는 2가지의 option이 있습니다.(2가지의 선택지)

1. Extra Zero Entries padded
   설명이 나와있지 않지만, 추가적인 parameter가 없는 것으로 보아 dimension을 맞춰주기 위해 0값으로 채워져있는 channel을 insert하여 dimension을 맞춰주는 것으로 생각됩니다.(아니면 알려주세요)

2. Eqn(2), projection shortcut을 사용하여 dimension을 맞춰줍니다. (1x1 convolution)

Dotted Line일때는 MaxPooling을 적용하여 size가 halved되기 때문에 1번과 2번 모두 stride를 2로 설정합니다.

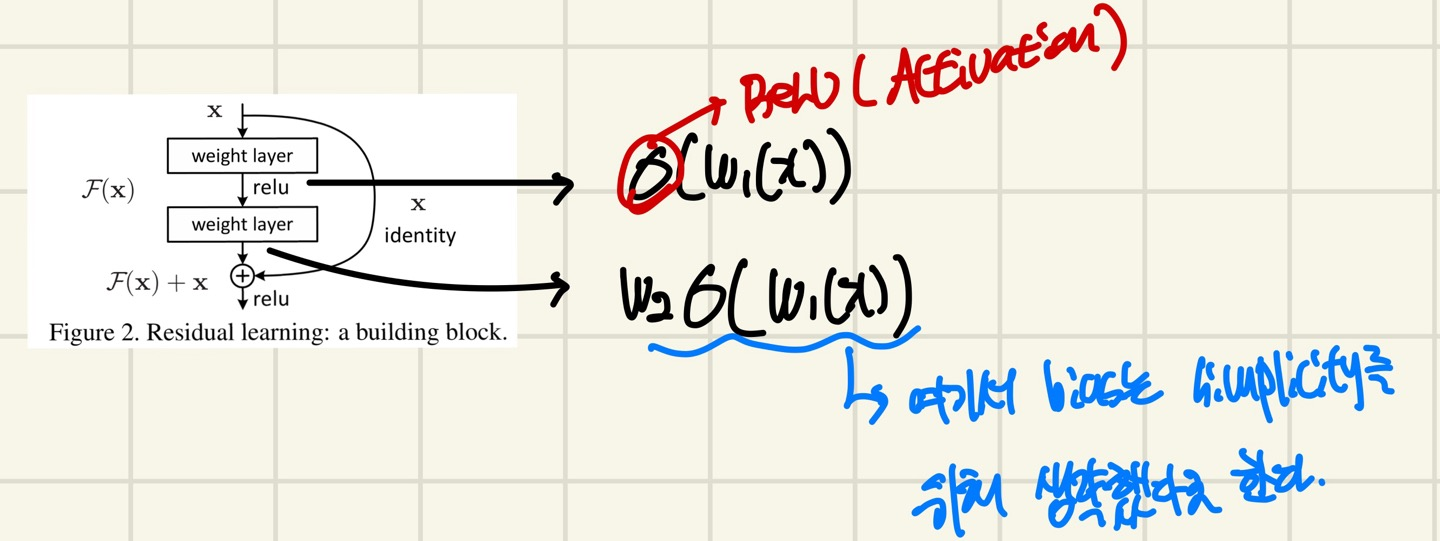
VGG, Plain, Residual 아키텍처는 다음과 같습니다.

Implementation

• Scale : image에서 더 작은 쪽은 [256, 480] range로 randomly sampled하고 224x224로 randomly crop한다.

• Horizotal Flip 적용

• per-pixel mean값을 빼준다.

• Activation 들어가기전에 BN 사용

• weight init : He(kaiming) init 사용

• SGD with Batch size : 256

• learning rate : 0.1(만약 error가 정체되면 10으로 나눠줌)

• $60 * 10^4$ 수행

• momentum : 0.9, weight decay : 0.0001

• No use Dropout

---

Experiments

ImageNet classification만 다룹니다.

Plain Networks

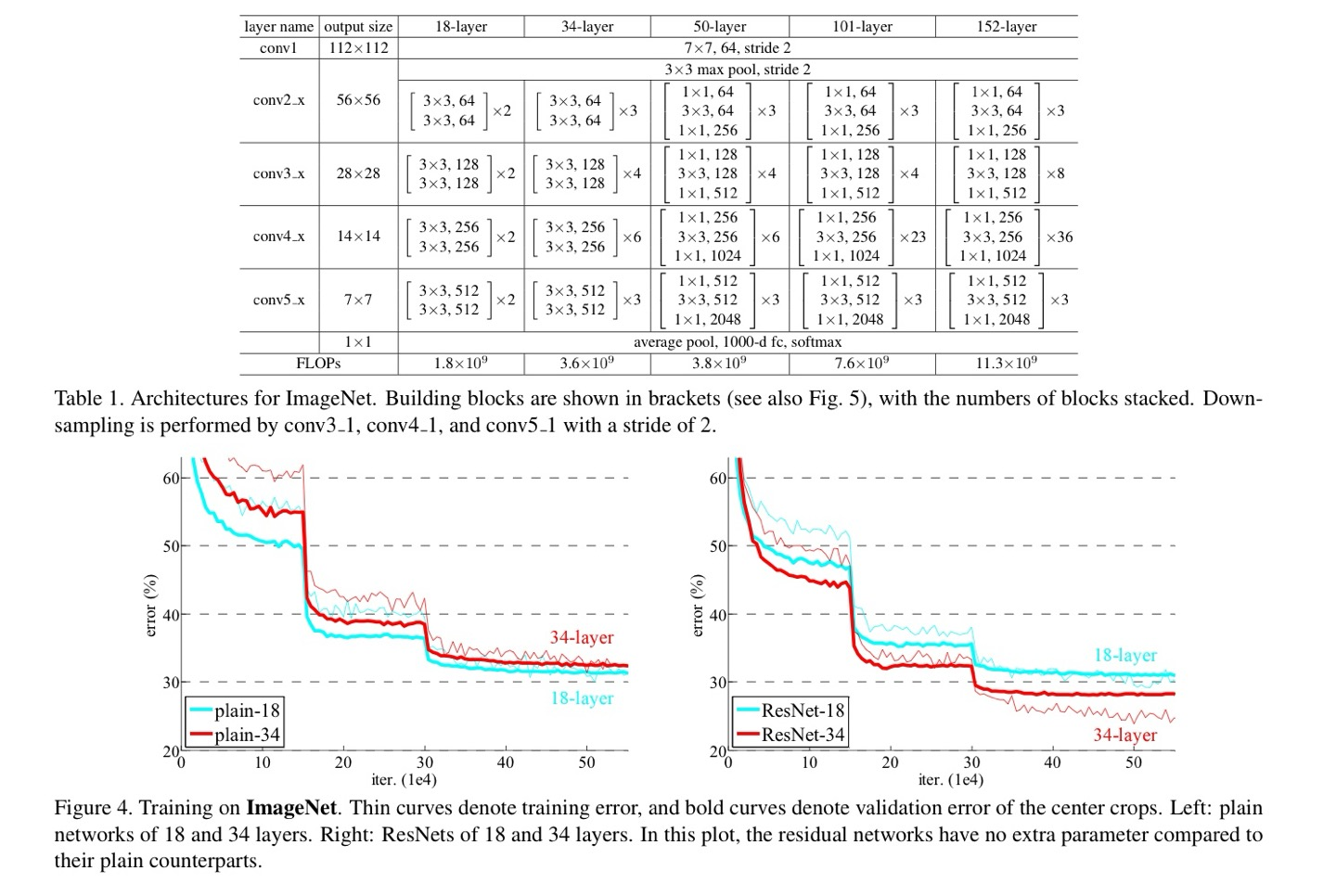
Table 1에 있는 18-layer와 Figure 3 중간에 있는 34-layer로 evaluate을 해보았다고 한다.
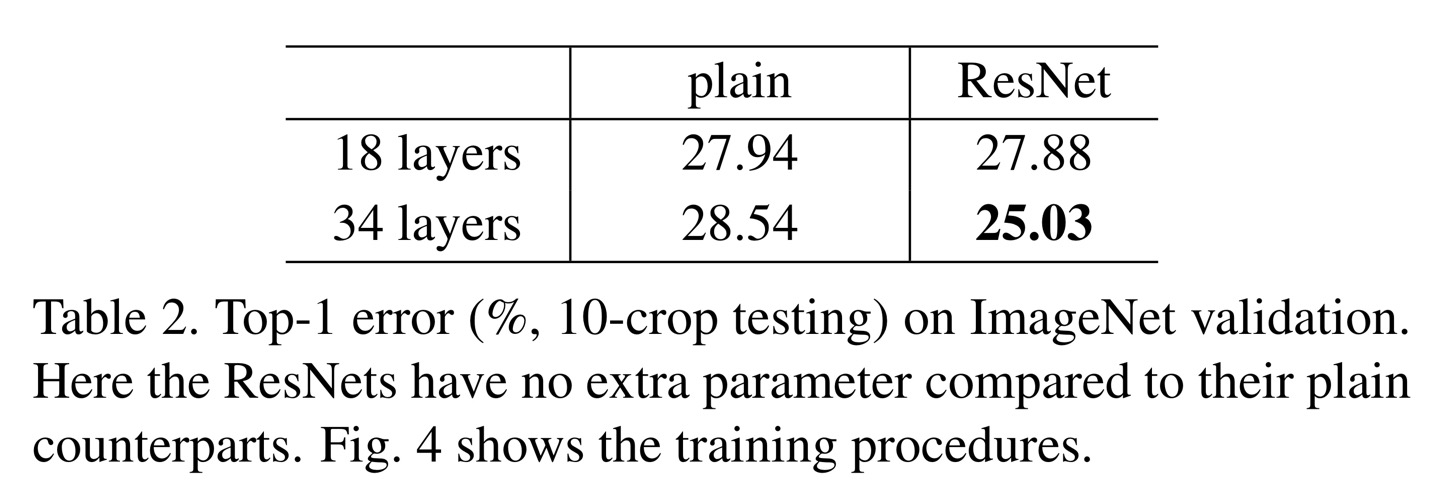
34-layer는 18-layer보다 validation error가 높은 result를 보였고 Table 2(Left)에 나타나져 잇다.
18-layer가 34-layer의 subspace임에도 불구하고 34-layer의 validation error가 높음을 확인하였다고 한다.(degradation)

하지만 34-layer의 최적화 문제는 gradient vanishing의 문제가 아닌 것으로 판별이 났는데, 이는 backpropagation의 과정에서 gradient들이 healthy norm을 보였기 때문이다. 실제로 34-layer는 competitive한 accuracy를 가지고 있었으며, 34-layer는 exponentially low convergence rate를 가지는 것으로 추측한다고 한다.

Residual Networks

18, 34 plain network에서 identity mapping을 통한 shortcut만을 추가한 residual network이며 Figure 3에서 dotted line을 적용할때 앞에서 dimension을 맞추기 위한 2가지 방법중 첫번째 방법인 extra zero padded방법을 이용했다고 하며 이는 설명한 것과 같이 추가적인 parameter는 없었다고 한다.

이 실험에서 중요하게 볼 3가지가 있다.

1. 34-layer가 18-layer보다 더 좋았으며 validation data에 generalizable 하다는 것이다. 이는 degradation의 문제를 이러한 구성(residual leraning)을 통해 해결할 수 있었고 increased depth를 통해 more accuracy를 얻을 수 있었다고 한다.

2. 34-plain과 비교해보면 34-residual layer이 3.5%의 더 낮은 error를 보였으며 이것도 extremely deep network에 residual learning이 효과적인 방법이라는 것을 말한다.

3. 18-plain net와 18-residual net를 비교해보면 18-residual net이 더 빠른 covergence 속도를 보였다고 한다.
   ResNet은 초기 단계에서 convergence를 더 빠르게 함으로써 optimization을 용이하게 한다고 합니다.

Identity vs Projection Shortcuts

Shortcut에 관한 이야기이며 3가지 option(선택지)가 있다고 한다.

A : zero-padding shortcut(오직 dimension을 키울때만, param-free)

B : Projection shortcut 사용(오직 dimension을 키울때만), 다른 shortcut은 identity

C : 모든 shortcut이 projection shortcut

성능은 C > B > A이며 모두 아주 미미한 성능 차이를 보였기 때문에 memory와 time-complexity, model size를 줄이기 위해서 C는 사용하지 않는다고 한다.

B > A인 이유는 A에서 zero padded된 dimension들이 residual learning을 하지 않았기 때문이고, C > B는 projection shortcut을 수행함으로써 추가적인 parameter가 기여했기 때문이다.

Deeper BottleNeck Architectures

training time을 고려하여서, building block을 bottleNeck으로 modify하였다고 합니다. F에서 layer가 2개 대신, 3개로 1x1, 3x3, 1x1 convolution layer로 구성하였고 1x1 convolution은 dimension을 줄이거나 늘릴 수 도 있다.(Figure 5의 right)

만약 shortcut이 identity가 아닌 projection으로 구성된다면 time-complexity와 model size가 2배로 늘어나기 때문에, Identity vs Projection Shortcuts의 마지막 문장에서 bottleNeck구조에서 identity mapping이 중요하다고 말한다.

ResNet50은 2-layer의 building block을 3-layer로 구성하였고 dotted line의 dimension을 맞추는 것은 B로 선택하였다고 한다.

ResNet101, ResNet152sms 더 많은 3-layer block을 이용하였으며, 매우 많은 depth로 구성되었음에도 불구하고 VGG-16, VGG-19보다 complexity가 낮았다고 한다.

---

코드 구현

ResNet 코드 구현

읽어주셔서 감사합니다~~:>