Abstract
VGG는 Convolutional Network의 depth가 large-scale image에 accuracy에 미치는 effect를 조사합니다. 즉 layer를 더 깊게 구성하여, 정확도에 얼마나 영향을 미치는지 연구하였다고 합니다.
layer를 깊게 구성하는 방법은 3x3 Conv filter를 사용하여 depth를 키웠다고 합니다.
ImageNet 이미지의 국한되어서 작동하는것이 아닌, 다른 image에서의 Error rate도 작았다고 합니다
가장 핵심 포인트는 3x3의 filter만 사용했다는것이 중요합니다.
왜 이러한 filter를 적용했는지 자세히 나옵니다.
Introduction
Abstract의 내용과 비슷한 내용입니다.
모델을 구성하는 Important aspect는 depth를 중점으로 연구했다고 합니다.
Layer의 depth를 증가하면 Performance가 좋기 때문입니다.
Non-Linearlity가 증가하기 때문이라고 볼 수 있습니다.(뒤에 더 자세히 나옵니다)
Feature extractor에 3x3 filter만을 적용하면서, depth를 키우는것이 가능했다고 합니다.
Convnet Configuration
Architecture
모델이 학습할때 image의 fixed size는 224x224입니다.
Image를 input할때, Preprocess는 RGB값들의 mean값을 빼주었다고 합니다.
즉, training set의 R,G,B의 평균을 구하고 각 Image의 R channel에는 전체 training set의 R 평균값을 각 pixel에 빼주는것이 됩니다.(각 G,B Pixel값에도 마찬가지이다)
이러한 과정은 input image를 Normalization 합니다.
앞에서 이야기한 3x3 filter를 적용하는 이유는 Input image의 feature를 추출하기 위해 최소한의 크기라고 합니다.
(left/right, up/down, center의 개념을 포착할수있는 최소한의 단위)
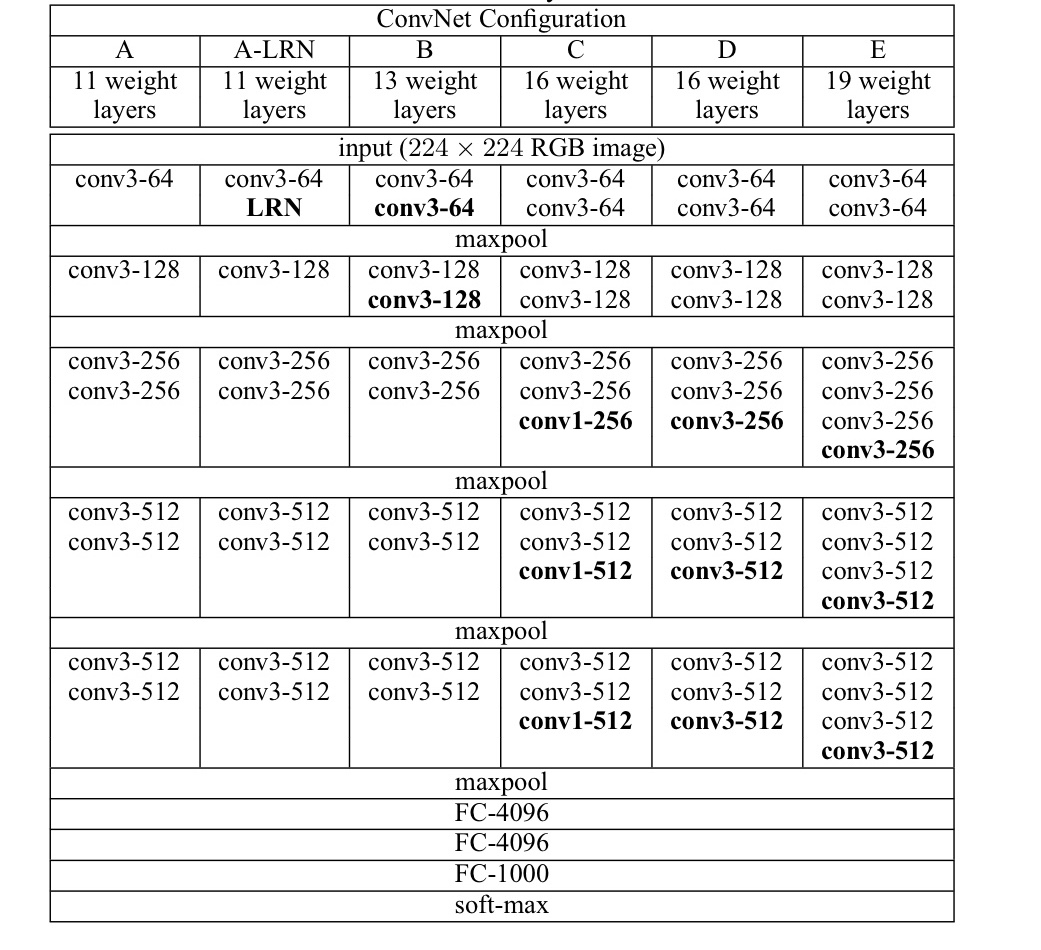위에 표는 VGG가 11 weight layers부터 19 weight layers까지 다양합니다
VGG11은 11 layers를, VGG16은 16 layers를 의미합니다.
이러한 Configurations들 중, C(16 layers)만 conv1(1x1 conv filter)를 적용했습니다.
1x1 Conv filter를 적용하면, non-linearity가 증가하고 channel수를 조절, 연산량이 감소합니다.(뒤에 더 자세히 설명합니다.)
- padding : 1 pixel
- 5개의 MaxPooling layer(kernel_size = 2, stride = 2)
FC(Fully Connected layer)에는 3개의 layer가 있고, 4096 channels가 존재하며, 1000개의 이미지를 분류하기 위해 마지막 layer에는 1000개의 channels가 존재합니다.(Activation function으로는 softmax)
모든 Hidden layer에서는 ReLU Activation Function을 적용했습니다.
그래프를 보면 A-LRN에서의 Model에서만 LRN(Local Response Normalization)을 적용하는것을 볼 수 있습니다.
LRN을 적용해도, Performance가 향상되지 않았으며 오히려 메모리 낭비와 Computation time만 길어졌다고 합니다.
Configurations
Conv layer를 거치면서 Feature map의 크기는 작아지고(각 뉴런의 receptive field는 커지게 되겠죠?) conv filter는 64에서 512가 될때가지 MaxPooling 적용 후 x2씩 적용된다고 합니다.
위의 표는, 모델의 Parameter수를 나타낸 것 입니다.
이러한 모델들은 더 큰 Conv layer와 receptive field를 가진 모델들보다 Parameter의 수가 적다는 것을 알 수 있습니다.(이러한 이유는 1x1 Conv filter와 관련이 깊습니다.)
Discussion
Parameter
7x7의 single conv filter보다 3개의 3x3 conv filter를 쓰는 이유를 예시로 설명하고있습니다.
첫번째로, 3x3 conv filter는 더욱 향상된 discriminative(식별력)을 가지고 있습니다.
왜냐하면, filter를 적용하고 Activation function으로 ReLU를 적용하기에 non-linearity가 향상됩니다.
그래서, 더 복잡한 문제를 잘 풀어낼 수 있습니다.
두번째로, Parameter의 개수가 줄어듭니다.
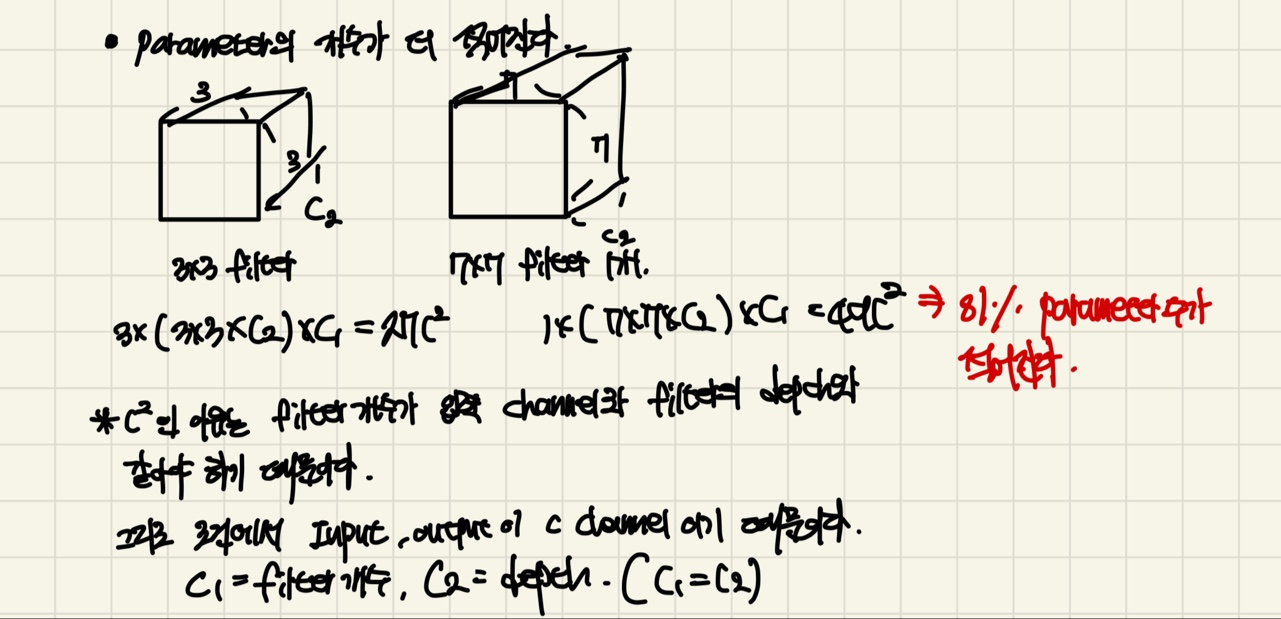들어오는 Input의 channel과 output의 channel이 같다고 한다면, 3x3의 filter와 7x7 filter의 depth가 서로 같습니다.(그림에서는 각 filter를 C2로 정의합니다.)
또한 Input과 output의 channel이 같기 때문에 filter의 개수도 같습니다. (그림에서는 C1으로 정의합니다.)
먼저 3개의 layer를 가지고 있는 3x3 filter를 먼저 보겠습니다.
3x(3x3xC2)xC1은 전체 Parameter의 개수입니다. 맨 앞 3은, filter를 적용하는 횟수, 3x3은 kernel_size, C2는 channel, C1은 filter의 개수가 되겠습니다.
식을 계산해보면 27C2XC1이 되지만, C2 = C1이니, 이 됩니다.
Single layer를 가지고 있는 7x7 filter는, 1x(7x7xC2)xC1으로 계산이 되는데요.
1은 filter를 적용하는 횟수, 7x7은 kernel_size입니다.(앞선 3x3 filter와 C1,C2는 같습니다.)
식을 계산하면 이 됩니다.
과 을 비교한다면, 이 81%의 Parameter수가 줄어들게 됩니다.
신기하게도, 더 많은 filter의 적용 횟수가 많은데도 불구하고 Parameter수가 줄어들게 되니, overfitting(과적합)을 방지하고, Computation 횟수가 줄어들어, 학습속도가 빨라집니다.
1x1 filter
Convnet Configuration의 Architecture의 A~E까지의 모델들은 보시면, 모델C에서 1x1의 Conv filter를 사용하는 모습을 볼 수 있습니다.
C에서는 비록, input과 output의 dimensionality(depth)가 같지만, ReLU로 인한 non-linearity를 포함한다고 설명합니다.
첫번째로, non-linearity의 증가와 Computation의 감소를 이끌어냅니다.
output의 결과를 (64,28,28)의 결과로 이끌어내보겠습니다.
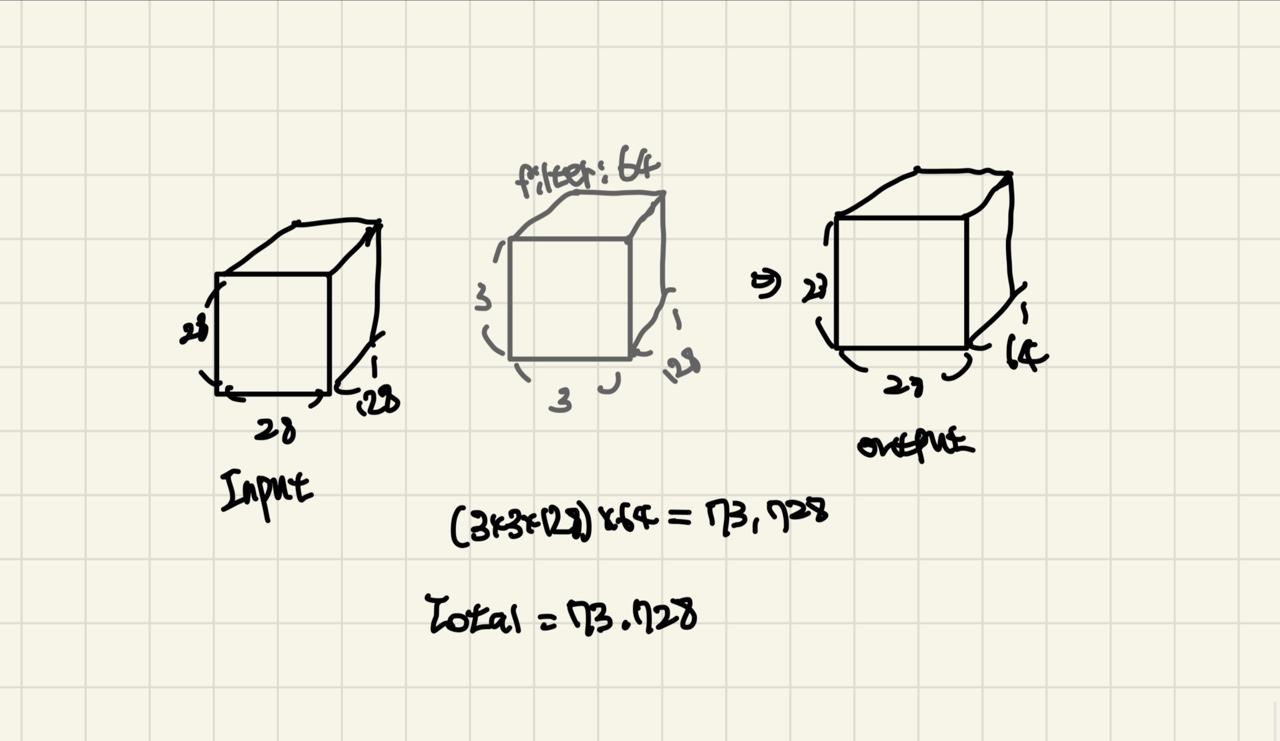
위 그림은 단순한 3x3의 filter를 적용합니다. filter의 channel은 Input의 channel과 같아야하니 128이 되겠습니다. filter의 개수는 64개가 되겠네요.(output의 channel을 64로 맞춰야하니, filter의 개수는 64가 됩니다.)
그렇다면 (kenel_size x channel) x filter 개수가 됩니다.
즉, (3x3x128)x64가 되므로 총 73,728개의 Parameter가 존재하게 됩니다.
output의 결과값에 ReLU의 Activation을 적용합니다.
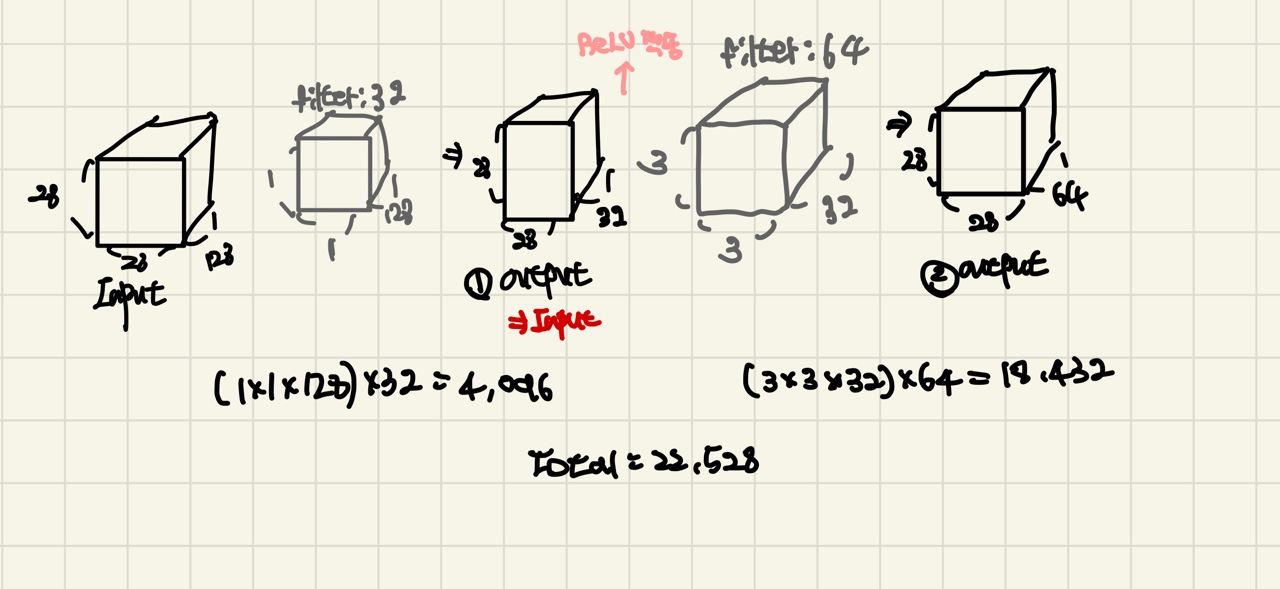
위 그림은 1x1 filter를 적용하고, 3x3 filter를 적용합니다.
1x1 filter를 적용하게 되면, (1x1x128)x32가되고, output의 ReLU를 적용하게 됩니다.( (1)output은 (2)output을 위한 input입니다.)
이후, 3x3 filter를 적용하고,(3x3x32)x64의 parameter, 또 output의 ReLU를 적용합니다.
(ReLU를 2번 적용하게 됩니다.)`
filter의 Parameter수를 계산하게 되면, 1x1 filter는 4,096개, 3x3 filter는 18,432개가 됩니다.
총 22,528개의 Parameter수를 가지게 됩니다. 즉, 바로 3x3을 적용하는것보다 1x1 filter를 적용한 후의 Paramter수가 적다는 것을 알 수 있게 됩니다.
Parameter수가 적으니, Computation의 횟수도 줄어들고 ReLU의 적용 횟수도 늘어나기 때문에 non-linearity가 증가하게 됩니다.
하지만, Channel을 잃게 되니 공간적인 정보를 잃게 되지만 Image의 feature들은 대부분 특정영역에 몰려 있기 때문에 Channel을 잘 축소 시키면 손실이 적어 지게 됩니다.(이후에 자세히 포스팅 할 예정)
두번째로, Channel의 수를 조절할 수 있습니다.
앞선 1x1 filter의 예시를 보면, 임의로 output의 channel수를 32로 설정한 것을 볼수있습니다.
물론 더 많은 channel의 수로 output의 depth를 조절 할 수 있지만, 1x1 filter를 쓰는 이유는 Computation의 감소하는데에 의의가 있으므로, 알맞은 channel을 설정 할 필요가 있습니다.
(의도적으로 weight의 개수를 늘릴 수 있습니다.)
Classification Framework
Training
- Mini batch 사용, batch size는 256
- optimizer는 Momentum 사용, hyperparameter는 0.9
- dropout 사용, ratio는 0.5 (FC first, FC second에 적용)
- Learning rate = 0.01로 초기화 (만약 val accuracy가 향상 되지 않으면, x0.1 해주었다.)
- weight decay는 L2 사용, hyperparameter는 5x0.0001
논외로, Lasso(L1 Regularization)과 Ridge(L2 Regularization)에 대해서 알아보겠습니다.
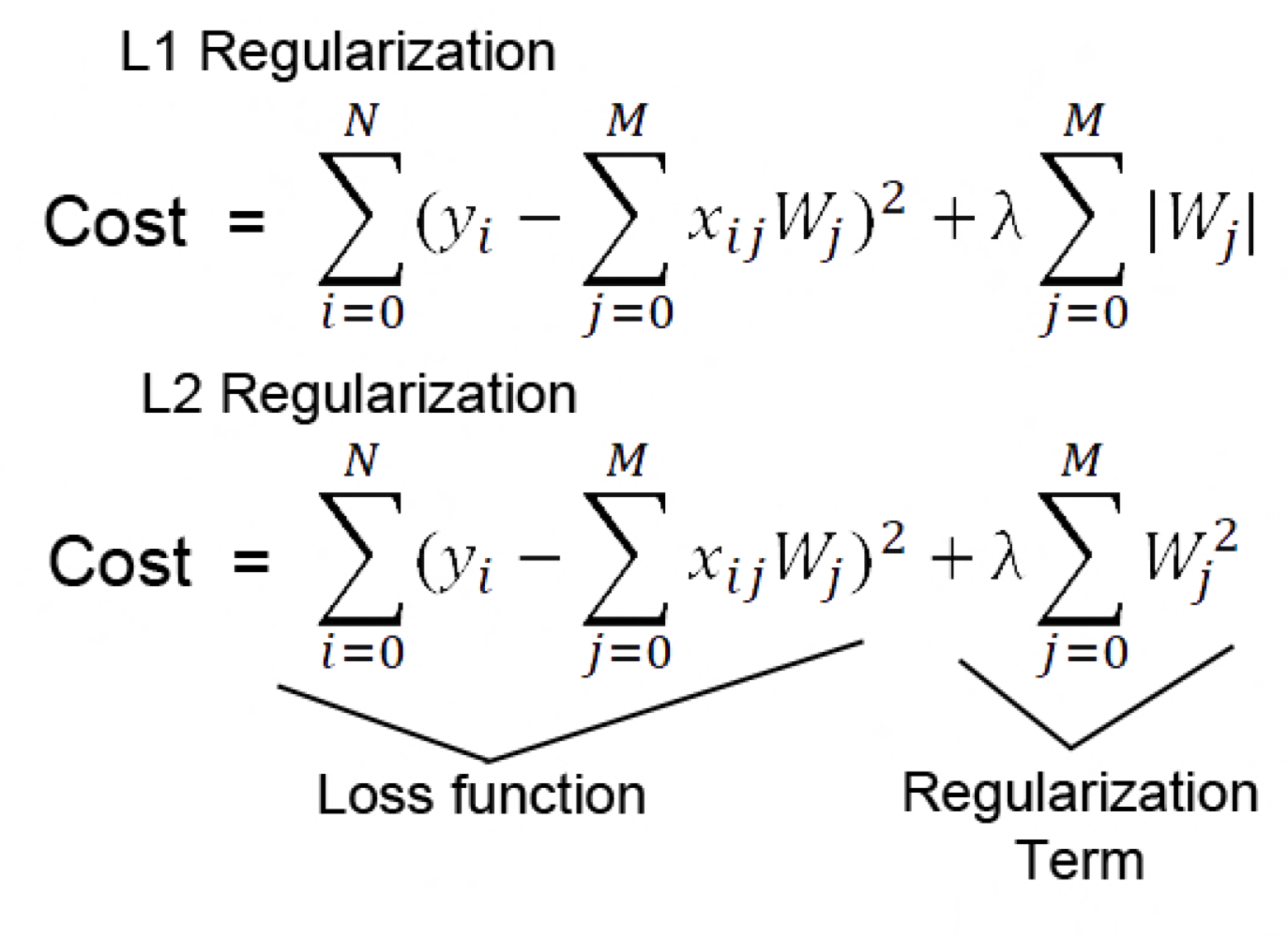손실함수(Cost)에 L1은 절댓값 가중치를, L2는 가중치의 제곱값을 손실함수에 더해주고 있습니다.
L1은 편미분시 가중치의 부호만 남기 때문에 가중치의 크기에 따라 규제의 크기가 변하지 않기 때문에 Regularization의 효과가 L2에 비해 떨어집니다. 또한 0에서 미분이 불가능합니다.(0에서 불연속점)
L2는 가중치의 크기만큼의 Penalty를 줄 수 있기 때문에, 특정 가중치가 너무 커지는 weight decay가 가능합니다.
람다(λ)는 hyperparameter이며, 람다 값에 따라 Penalty를 조절 할 수 있습니다.
더 자세히 알아보고 싶으시면, 여기 클릭하세요.
Weight Initailisation의 중요성
모델의 가중치가 instabilty한 값으로 초기화 된다면, backpropagation에서 gradient가 instability 해집니다.
VGG는 가중치의 초기화의 방법은 다음과 같습니다.
먼저 모델A에게 weight값을 random으로 초기화하고 학습을 진행시킵니다.
충분히 학습이 되었다면, 모델A의 학습한 가중치를 처음 4개의 Conv Layer와 FC Layer에 가중치 값을 초기화 시켜줍니다.(나머지 layer들은 random값으로 초기화 시켜줍니다.)
이때 random으로 가중치를 초기화 시킬때, 평균은 0, 분산은 0.01로 가중치를 초기화 시켜주었습니다.(Bias는 0으로 모든 Layer에 초기화)
모델이 학습할때 224x224의 fixed size를 얻기 위해 resclaed training image에서 random crop을 해주었습니다. crop한 image는 Random Horizontal과 Random RGB shift를 적용해주었습니다.(바로 다음에 자세히 설명)
Training image size
먼저 S는 isotropically-resclaed training image에서 width와 height값 중 작은 값입니다.
학습 시 Input Image는 224x224로 고정되어 있지만, S는 224보다 더 큰 값을 가질 수 있습니다. S = 224 전체적인 측면 학습이 가능해지고, s > 224이면 특정 부분의 학습한 것을 반영 할 수있습니다.
isotropically-rescaled image란 이는 width와 height에 동일한 ratio를 적용하여 이미지가 한 축을 따라 왜곡되지 않도록 하는 것을 의미합니다.
예를 들어 S = 512 라면, width = 1024, height = 2048에서 더 작은 쪽(width)를 512로 줄여줍니다. 이때 apsect ratio를 지켜야합니다.(1:2의 비율이니 rescaling할때에도 width와 height의 비율이 1:2여야한다.)
그러면 width = 512 height = 1024로 rescaling됩니다.
이 말을 더 구체화 한 방법이 2가지가 있습니다. (즉, S값을 설정하는 방법이 2가지가 있다.)
첫번째로 Single-Scaled 입니다
S = 256과 384로 설정했다고 합니다.
먼저 S = 256인 값으로 모델을 학습시키고, S = 384일때의 훈련 속도를 높이기 위해 S = 256에서 훈련한 가중치 값들을 초기화 시켜준다고 합니다.
이때의 가중치 값들은 어느정도 훈련이 된 값들이기 때문에 학습률(Learning Rate)의 값을 0.001로 설정했다고 합니다.
두번째로 Multi-Scaled 입니다.
S값을 고정 시키지 않고, 256 ~ 512값으로 randomly하게 rescaled 해주었습니다. (S값을 무작위로 바꾼다 하여 Scale Jittering 이라 합니다.)
Image들의 크기는 모두 다르기 때문에 Multi-scale image방법은 Input Image의 size에 대응이 가능하기 때문에 학습효과가 좋습니다.
빠른 학습을 위해 S = 384로 single scaled한 pre-trained 모델의 모든 Layer를 fine-tuning(미세 조정)하여 Multi-scaled image를 훈련시켰다고합니다
Testing
이 부분에서 Testing이라고 했지만, Testing이 아닌 validation이 맞다.(Test image는 augmentation을 거의 해주지 않는다.)
먼저 Q는 train image의 S와 같은 역할을 한다.(validation image의 더 작은 부분)
만약 S와 Q값은 같지 않아도 된다. 각 S값에 여러개의 Q값을 적용하는것은 더 나은 Performance를 보여준다고 한다.
모델을 Validation할때는 FC Layer들 대신, Conv Layer를 추가한다.(Fully Convolutional Network 라고한다.)
즉, 모든 Layer들이 Convolutional Layer로 이루어져있다.(모델의 Train과 validation의 구조가 서로 다르다.)
FCN을 사용하면, 기존 FC Layer의 단점인 이미지의 위치 정보가 사라지는것을 방지하고 Input Image의 size가 고정된 값만을 사용하는 조건이 없어진다.
FC Layer의 첫번째는 7x7 Conv layer, 나머지는 1x1 Conv layer를 갖는다.(filter임)
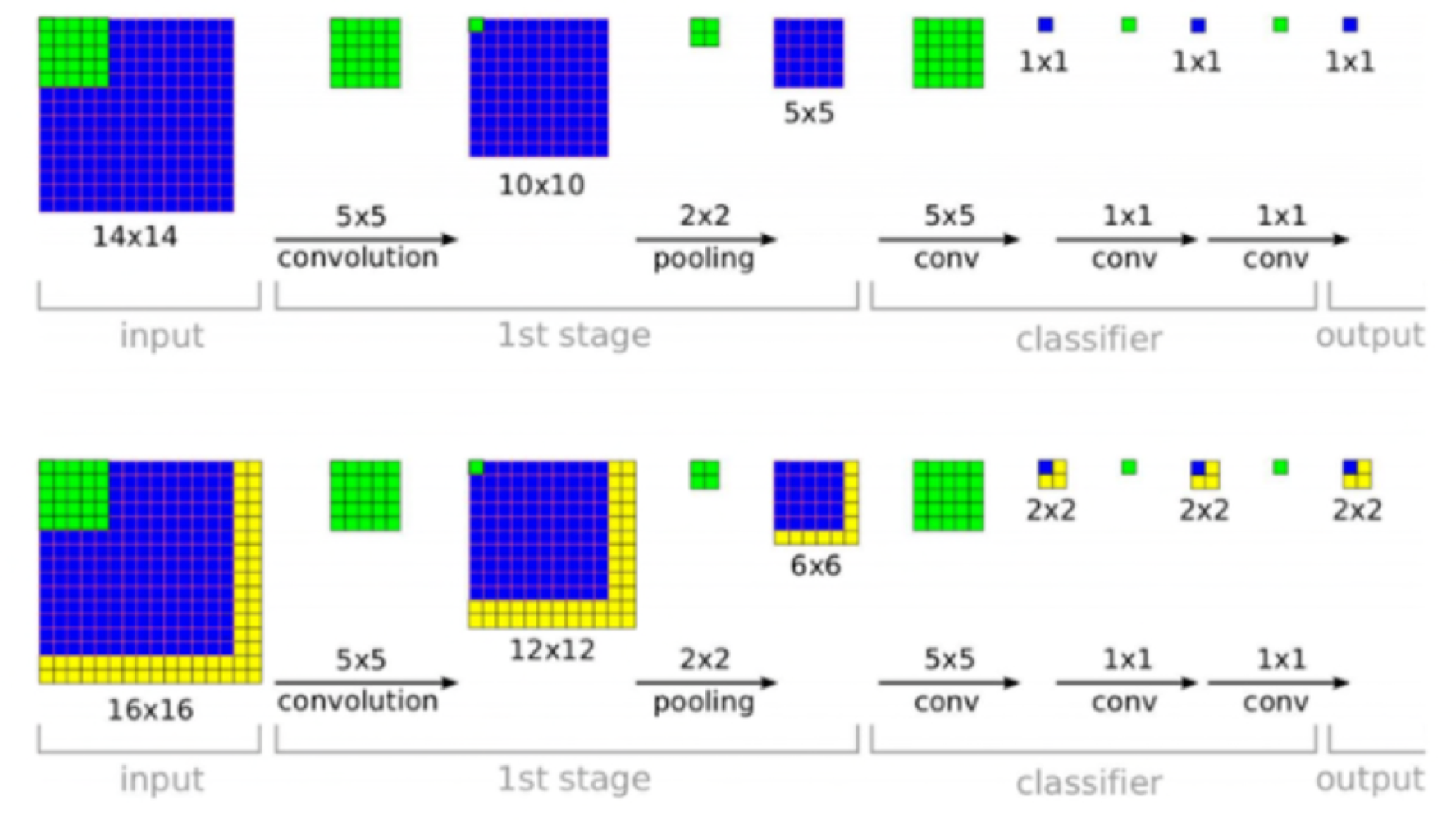사진 참고
위 그림의 예시를 보겠습니다.
필자는 fixed-size vector를 얻어야하기 때문에 1x1의 output값을 얻어야합니다.
Input Image의 size가 14x14이면, output이 1x1로 나왔지만, Input Image의 size가 16x16이면, 2x2의 output 결과 값을 보여줍니다.
이에 대한 해결책은 2x2에서 sum-pooled 해주게 됩니다.(averaged 해준다고 합니다. 2x2에서 평균을 구하고 평균값을 대표값으로 사용합니다. 논문에서는 적혀 있지 않지만 Global Average Pooling 같습니다.)
또한 Validation Image의 Horizontal Flip을 적용한다고 합니다.
요약하자면, Scaling후, Crop과 Horizontal Flip으로 validation image수를 늘렸고, 1개의 이미지에서 추출한 여러개의 Image를 모델에 입력하여서 나오는 결과 평균으로 최종 Class를 결정하게 됩니다.
Multi-Crop과 dense evaluation은 서로 상호보안적(적절히 잘 섞어 사용한다면) 성능이 더 좋아진다고 합니다.
Dense Evaluation은 padding을 실행할 때, 이웃한 값으로 padding을 적용하기 때문에 receptive field가 증가합니다. 그래서 더 많은 Context를 포착하기 때문에 학습효과가 좋습니다.
Multi-Crop은 Image를 여러 개의 크기가 동일한 패치로 자르는 방식을 사용합니다. 예를 들어서 224x224 크기의 Image를 4개의 패치로 나누어 처리하면, 이 패치들은 Image의 서로 다른 영역을 나타내고, 모델은 여러 개의 독립적인 입력을 처리함으로써 전체 이미지의 다양한 특징을 인식할 수 있습니다.
이러한 패치들은 모델에 입력되고 각각의 출력을 얻으며, 이후 이 출력들은 보통 pooling의 방법을 사용하여 1개의 예측 결과로 결합합니다.
Dense Evaluation에 예를 들어서 설명하자면, FC Layer로 전달하기전에 MaxPooling으로 대표적인 정보만 추출할때 표현력이 떨어지므로 MaxPooling을 Densly하게 적용하면 Resolution이 많이 떨어지지 않습니다.(stride : 2 에서 stride : 1로 적용하는것처럼)
Classification Experiment부분은, 통계자료를 설명하는 글이기 때문에 생략하겠습니다.
Conclusion
VGG를 연구하면서 결국에는 Hidden Layer의 depth가 많아야지 Image Classification의 Performance가 좋아진다는 것을 알게 됬다고 합니다
또한 다른 Image에 대해서도 generalise한 Performance를 보여주었습니다.
따라서, Visual Representation(시각적 표현)에서는 depth가 정말 중요하다는것을 깨달았다고합니다.
코드 구현
여기 코드 구현했습니다. 읽어주셔서 감사합니다 :)
