RNN, LSTM, GRU에 간단하게 RNN, LSTM, GRU을 설명했으니, 읽고 나서 해당 글을 읽는 것을 추천한다.

이 블로그 포스트는 Transformer의 강의의 내용을 정리 및 제가 알고 있는 내용을 덧붙여 설명한 글입니다.

Transformer를 이해하기 위해서는 Attention, Self-Attention을 이해해야하기 때문에 중요한 개념이라고 생각합니다.

RNN, Seq2Seq 한계점

RNN

RNN(순환 신경망)의 한계점은 Input data의 sequence가 길어지게 되면 hidden state들이 많아지게 된다. 이 sequence의 단어들마다 hidden state들에 누적해서 weight들을 곱해주게 된다.

이러한 문제점은, matrix끼리 곱하는 횟수가 많아지기 때문에 초반의 단어들에 대한 information이 없어질 확률이 매우 크다. 왜냐하면 weight의 값이 누적되어 값이 작아질 수 있기 때문이다.

Seq2Seq

Encoder-Decoder의 구조로 되어 있지만, Decoder에서 받는 context vector의 input dimension이 정해져 있다는 한계점이 존재한다. 이는 CNN에서 MLP로 넘어갈 때 input dimension이 정해져 있는 것과 똑같은 mechanism이다.

어쨋든, RNN기반의 Seq2Seq를 사용하였기 때문에 RNN이 가지고 있는 한계점으로 Context Vector에는 마지막 hidden state의 값이 클 확률이 매우 커, 초반에 가지고 있는 information이 적어지게 된다.

따라서, 이에대한 보안점으로 "Attention"기법이 나오게 된 것이다.

---

Attention

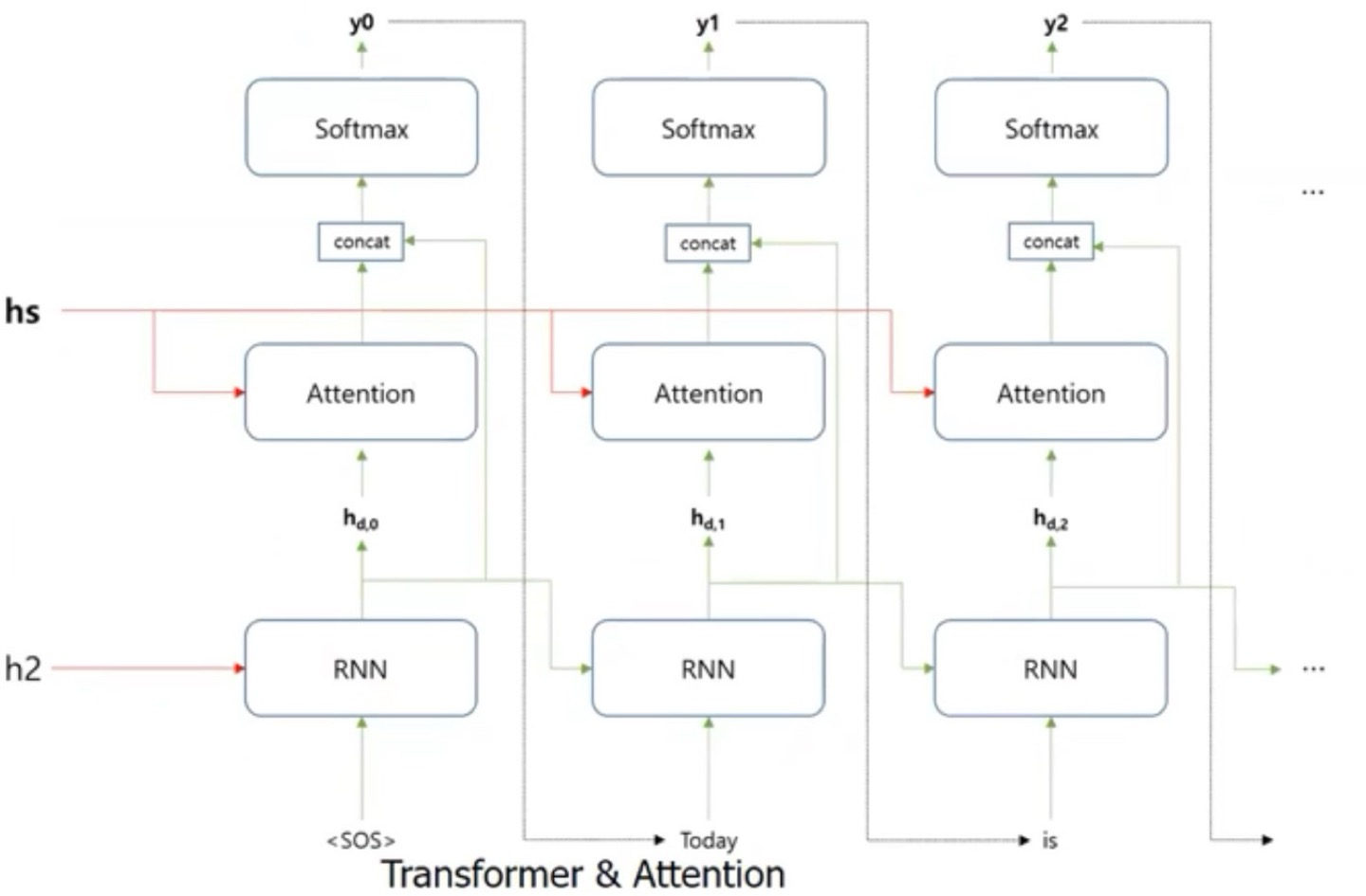
Attention을 적용한 Seq2Seq는 위와 같은 Decoder구조를 나타낸 것이다.
근데, attention을 적용했다고 Seq2Seq에는 RNN을 적용하지 않은 것은 아니니, 주의하자.

전체적인 Pipeline은 Encoder에서의 모든 input sequence의 단어들의 hidden state값들을 Decoder의 hidden state와의 dot product를 통해 similarity를 구해주게 된다.
이 값을 attention score라고 하며, 이 값을 softmax로 normalization시켜 weight를 해당 Decoder의 hidden state에 곱해주게 되고, Decoder의 hidden state와 Decoder의 hidden state에 weight(attention score)의 값을 concatenate을 해주고, 다음 layer에 input값으로 $y_0$를 보내줘야하기 때문에 input dimension을 맞춰주어야 한다.
따라서, concat을 하고 난 뒤의 weight를 곱해주게 되며, 그 뒤에 softmax함수를 적용하면 $y_0$가 나오게 되는 것이다.

예시

일단 전체적인 pipeline을 알았으니, 어떻게 되는지 예시를 통해 알아보자.

"오늘은 금요일 입니다"를 "Today is Friday"의 output이 나와야한다고 해보자
그러면 "오늘은 금요일 입니다" 부분은 Encoder에서 처리되고, "Today is Friday"는 Decoder부분에서 output값을 내야하는 것이다.

Word Embedding

$\begin{bmatrix}h_0\\h_1\\h_2 \end{bmatrix} = \begin{bmatrix}1&0&0&1&2\\1&0&0&1&1\\ 1&1&0&0&1\end{bmatrix}$로 $h_0$가 "오늘은", $h_1$이 "금요일", $h_2$가 "입니다"로 word embedding이 되어서 matrix로 output이 나온 결과라고 해보자

Attention Score

"Today"에 대한 hidden state값은 그럼 $h_{d,0} = \begin{bmatrix}1\\0\\0\\0\\2 \end{bmatrix}$로 하고, 이 값을 $\begin{bmatrix}h_0\\h_1\\h_2 \end{bmatrix}$와 dot product를 하면 된다.

$\begin{bmatrix}h_0\\h_1\\h_2 \end{bmatrix} * h_{d,0} =\begin{bmatrix}1&0&0&1&2\\1&0&0&1&1\\ 1&1&0&0&1\end{bmatrix}*\begin{bmatrix}1\\0\\0\\0\\2 \end{bmatrix}$를 계산하면 된다.

이 값의 결과는 $\begin{bmatrix}5\\3\\3\end{bmatrix}$으로 attention score를 가지게 된다.

Apply Softmax for Attention Score

weight의 값은 0~1사이로 normalization을 시켜야하므로, softmax함수를 통해서 positive의 값을 가지고 있고, softmax function은 xponential의 값을 사용하고 있기 때문에 큰 값은 여전히 큰 값을 가지고, 작은 값은 여전히 작은 값을 가지고 있다.

따라서 $softmax(\begin{bmatrix}5\\3\\3\end{bmatrix}) = \begin{bmatrix}0.8\\0.1\\0.1\end{bmatrix}$의 weight값을 가지게 된다.

이 값을 Encoder의 각각의 hidden state값에 곱해주면 된다.

Weighted Sum

$h_0 * 0.8 + h_1 * 0.1 + h_1 * 0.1$의 값이 weighted sum이게 된다.

각각의 Encoder의 hidden state에 mapping되는 weight의 값을 곱해주고, weighted sum을 해주면 되는 것이다.

Attention Output

weighted sum한 값이 나온 것은 attention의 output이고, 이 값을 앞에서 $h_{d,0}$와 concat을 해야하니, concat의 결과는 $\begin{bmatrix}(h_0*0.8, h_1*0.1, h_2*0.1),[1, 0, 0, 0, 2])\end{bmatrix}$값이 되고, input dimension이 3이라고 가정하면 이 값에다가 weight를 곱하여 output dimension을 3으로 맞춰주는 것이다.

$tanh(W_c, (concat)^T + b_c) = s_t$의 값이 나오고, 이 값을 다시 softmax함수를 적용하여 최종적인 $y_0$가 나오게 되는 것이다.

즉, $y_0 = softmax(W_yS_t +b_y)$가 최종적인 output이 되는 것이다.

---

Self-Attention

Self-Attention은 attention의 mechanism이고, input text data내에 존재하는 단어들 간의 관계를 파악하기 위해 사용되는 것 입니다.

기존의 attention의 문제점은 문장 간의 순서를 변경하여도 똑같은 output을 도출하여 문장의 sequence가 달라지더라도, 이를 참조하지 않았다는 단점과 동음이의어를 처리하지 못한다는 단점이 존재한다.

attention에서와 거의 비슷한데, Embedding vector에 attention score의 값을 곱해주기만 하면 된다. 나머지는 attention과 똑같게 값을 구해주면 된다. (굳이 설명안해도 이해가 되었을거라고 생각한다!!!!)

---

Transformer에서 Self-Attention

기존의 self-attention과 다르게, Transformer에서의 self-attention은 어떠한 단어에 더 많은 weight를 줘야하는지 Query, Key, Value 3개의 vector들을 사용하게 된다.
이 3개의 vector는 각각의 단어마다 있다는 것을 명심해야한다.

Query, Key, Value를 구하기 위해서 weight matrix$(W_Q, W_K, W_V)$가 각각 존재하게 된다.

• Query : 내가 관심있어하는 단어 vector

• Key : 특정 단어에 대한 Index 역할

• Value : Key에 대한 구체적인 정보를 담고 있다.

어쨋든 앞에서 attention의 pipeline을 본 것처럼 여기서도 한번 전체적인 pipeline을 알아보자

먼저 Query, Key, Value를 구하게 구하고, attention score를 통한 weight의 값들을 구하기 위해서 Query와 Key를 dot product를 해주게 된다. 당연히 softmax함수를 통해 weight의 값을 normalization을 해줘야하며, normalization된 값들을 Value에 곱해주고 weighted sum을 하게 되면 어떠한 단어에 더 많은 weight를 줘야하는지 값이 나오게 된다. (Embedding Vector에 곱해주면 된다.)

목표는 어떠한 단어에 weight를 더 줘야하는지 앞에서 본 self-attention과 똑같은 mechanism을 알 수 있다. 사실, attention mechanism이 이런 것이다.

어쨋든, 앞에서 본 pipeline을 수학적 수식으로 알아보자면, $Softmax(Q^TK)*V$가 된다.

다시 간략하게 설명하면, $Q^TK$는 attention score, 이를 $Softmax$를 통해서 normalization을 해주고, 해당 값을 Value matrix와 곱해주면 되는 것이다.

이를 matrix로 표현하면 위와 같이 나오게 되며, 해당 row vector가 Encoder의 word embedding에 곱해줄 weight의 값이 된다.

"Today"단어에 곱해줄 weight는 $[1, 2, 2]$이라는 소리이다.