영상처리2(Linear/Nonlinear filters)

홍성민·2023년 10월 4일

영상처리

영상 처리

목록 보기

3/7

Linear Operator

어떠한 사칙연산을 할때 우리는 분배법칙, 교환법칙과 같이 Linearity를 이용한다.
이러한 것은 domain에서도 Linearity가 성립한다.

H[f(x,y)] = g(x,y)라는 식에서 H라는 Transformation이 있고 이것을 Intensity, 즉 f(x,y)에 적용을 한 값이 g(x,y)라고 가정해보자.

그렇다면, H(a $f_1$ (x,y) + b $f_2$ (x,y)]는 aH[ $f_1$ (x,y)] + bH[ $f_2$ (x,y)]로 분배법칙이 성립이 된다.

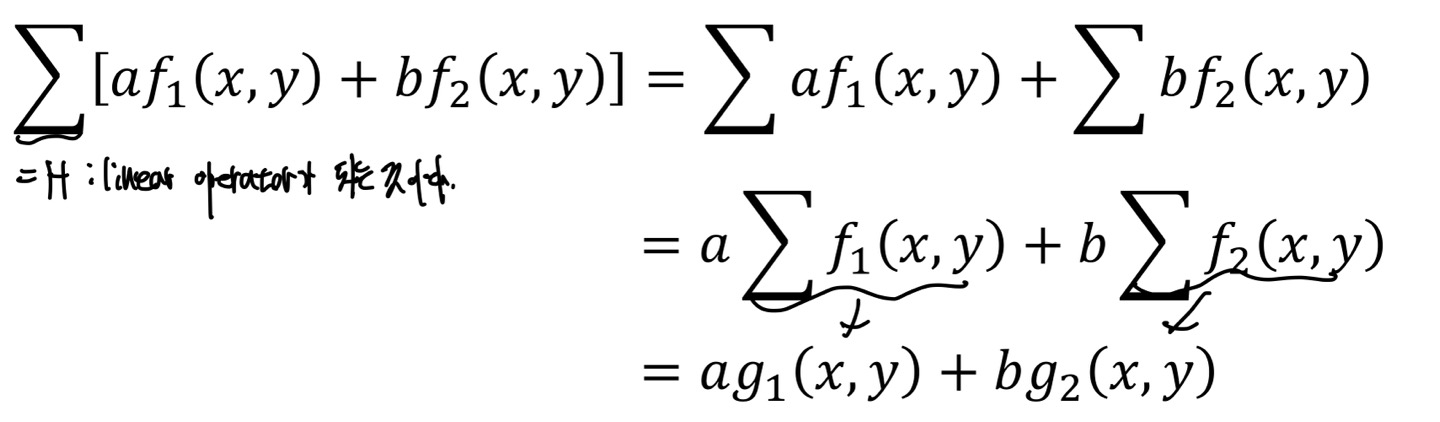
위의 그림의 식에서 $\sum_{}^{}$ 가 Transformation이 되는 것을 볼 수 있다.

Linear Filter

Linear Filter를 적용하려면 2가지의 단계가 있다.

각 Pixel에서 weight(filter의 element)를 곱해준다.
곱한 값을 모두 더해주면 된다.

즉, Input Image에서 filter의 weight를 element-wise로 곱해주고 곱한 값들을 더해주면 된다는 것이다.

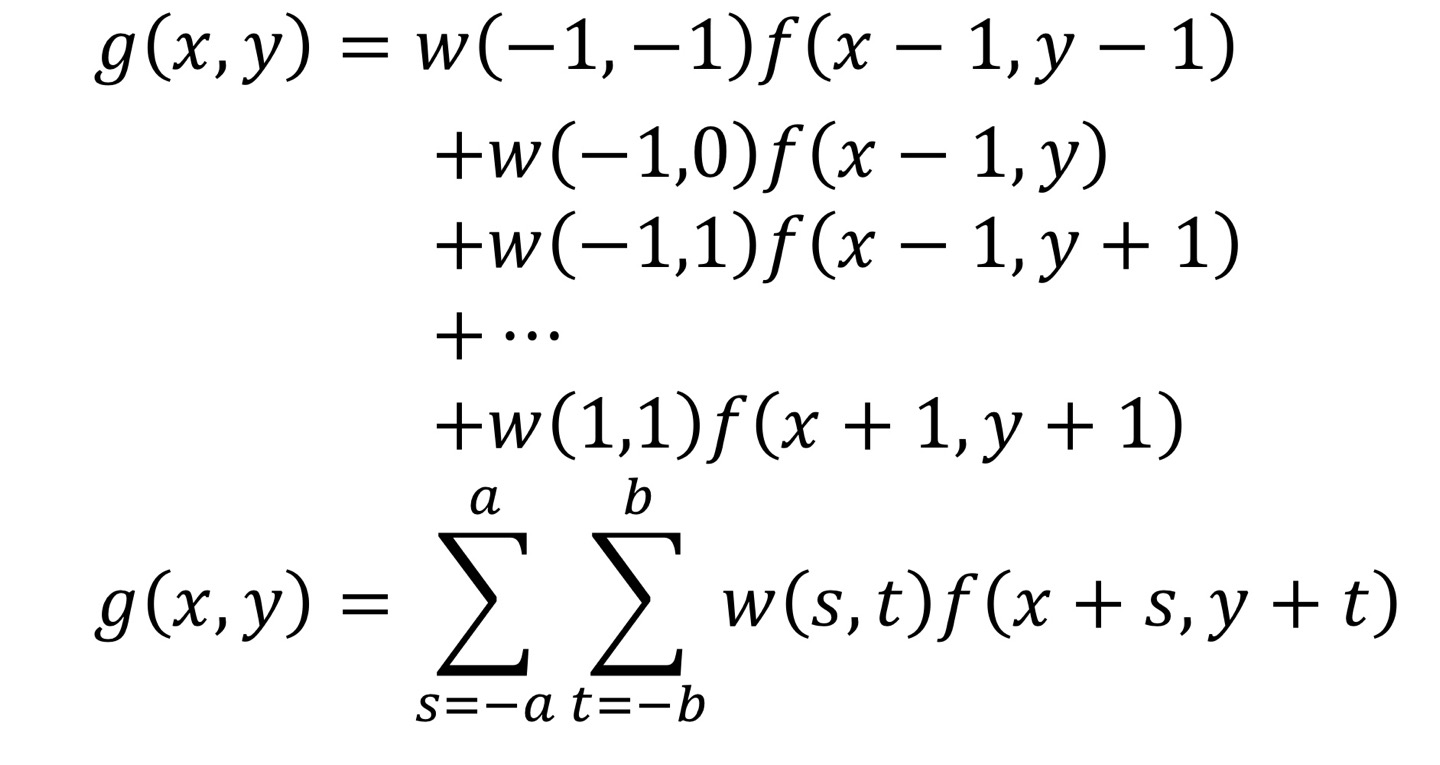
위의 식은 Input Image에 filter를 적용하는 연산을 수식으로 나타낸 것이다.

마치 위의 식은 Convolution의 연산이라고 생각할 수 있지만, Convolution이 아닌 Cross-Correlation 방법으로 적용한 것입니다. 이것은 다음 소제목에서 자세히 다룹니다.

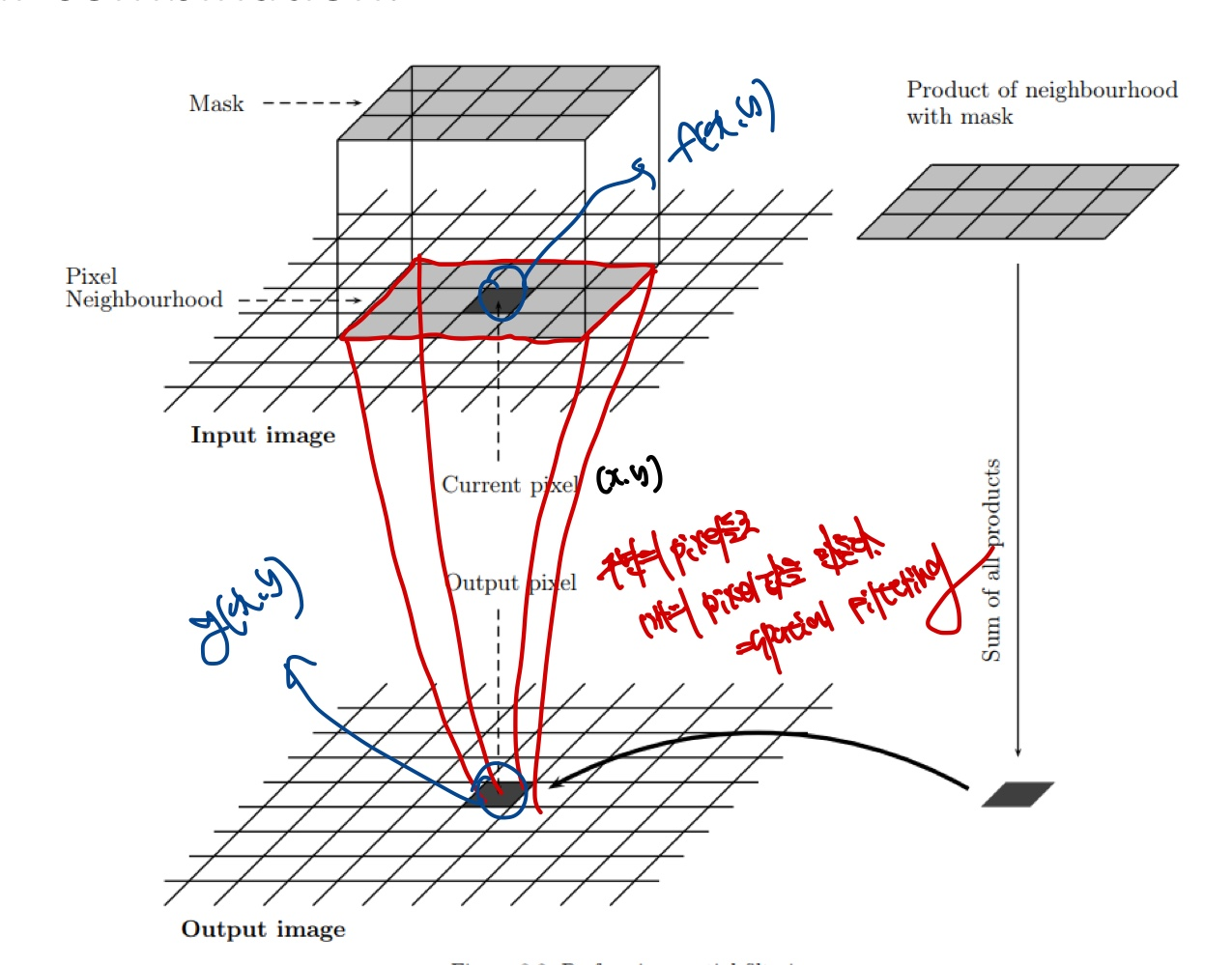
위의 그림은 Input에다가 Filter를 적용한 그림입니다.

파란색으로 쓴 Input Image의 f(x,y)를 Output Image의 g(x,y)로 변환시키기 위해 filter를 적용합니다. 이러한 filter를 적용할때 f(x,y)만을 이용해서 g(x,y)로 변환시키는게 아니고, f(x,y)의 주변 정보값(Pixel)들을 이용하기 때문에 "Spatial Filter"라고 불립니다.

조금 더 자세히말하면 Spatial Filtering이란, 영상 신호에 대하여 Spatial Domain에서의 Filter처리를 의미합니다.
Image에 있는 공간 주파수 대역을 제거하거나 강조하는 Filter처리이며, 사용하는 Filter의 계수에 따라서 특정 주파수를 제거하거나 강조할 수 있습니다.
영상에서는 Image에서 특정 부분을 강조한다고 생각하시면 됩니다. 여기서 말하는 것은 신호처리에서 다루는 내용입니다.

이러한 종류는 크게 2가지가 있습니다.

먼저 Low-Pass Filter는 신호 성분에서 저주파 성분은 통과 시키고 고주파 성분은 차단하는 Filter로, 잡음을 제거하거나 흐릿한 영상을 만들때 사용하게 됩니다. Filter는 모든 계수가 Positive인 값이고, element의 전체 합은 1이 됩니다.

High-Pass Filter는 신호 성분에서 고주파 성분은 통과시키고 저주파 성분은 차단하는 Filter로, 흐려진 영상을 개선하여 첨예화 같은 결과 영상을 생성합니다.

Cross-Correlation vs Convolution

먼저 우리가 Convolutional Neural Network에서 Convolution은 사실 Cross-Correlation이다.

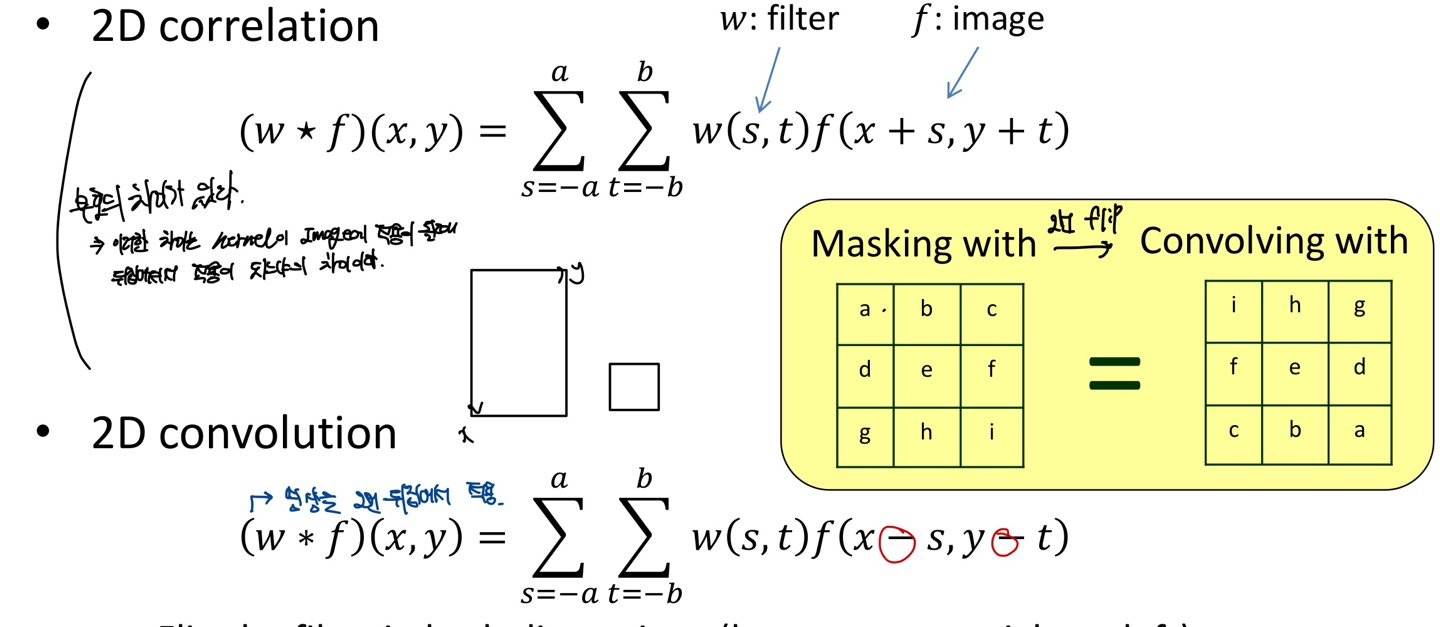
먼저 Convolution과 Correlation의 차이점은 image(f)에서 s,t의 부호가 서로 다르다는 것에 있다.

Convolution의 식을 그대로 쓰게 된다면, w(-1,-1)f(x+1,y+1) + w(-1,0)f(x+1,y) ...로 연산이 된다.
3x3 filter가 있다고하자. w(x,y)를 filter의 중점이라고 봐보자. 그렇다면 바로 위의 식에서 w가 filter라고 했으니 w의 (-1,-1)의 element를 f(x+1,y+1)을 곱해주는것으로 정의 된다.

하지만, 우리는 CNN에서 filter를 w(-1,-1)f(x-1, y-1)로 위치가 서로 mapping되는곳에서 계산을 이루어왔다.

Correlation 연산을 봐보자. w(-1,-1)f(x-1,y-1) + w(-1,0)f(x-1,y)...로 연산이 된다.
그렇다면 우리가 CNN에서 사용하는 Convolution연산이 실제로는 Correlation연산으로 볼 수 있게 된다.

만약 실제로 Input Image에서 Cross-Correlation연산을 해주는 것이 아니고 Convolution연산을 해준다면, Image를 bottom to top, right to left로 flip을 해주어야 Convolution연산이 된다.
Cross-Correlation연산에서 Convolution연산으로 바꾸고 싶을때도 마찬가지이다.

딥러닝에서는 이 두 용어를 혼용하여 사용하는 경우가 많고, 딥러닝 프레임워크에서도 Convolution연산이라고 부르기 때문에 Cross-Correlation을 Convolution이라는 용어를 계속 사용하고, 수학적으로 동일한 결과를 생성하기 때문에 Cross-Correlation을 사용하는 것이 직관적이며 코드 구현도 간단합니다. 즉, 수학적 편리성과 구현 효율성 때문입니다.

Box Filter vs Gaussian Filter

Box filter와 Gaussian filter 모두 고주파 신호를 차단하는 Low-Pass filter입니다.

먼저 Box filter를 적용한 그림을 보겠습니다.

영상의 결과를 보면 다음과 같습니다.

만약 filter의 크기가 3x3이라면 box filter는 $\frac{1}{9}$ $\begin{matrix} 1 & 1 & 1 \\ 1 & 1 & 1 \\ 1&1&1 \end{matrix}$ 이 됩니다.

즉 $\frac{1}{9}$ 에서 9는 element의 개수를 의미하고 모든 element의 합은 1이 됩니다.(Low-pass filter이기 때문)
주변 pixel들을 참조하는 개수만큼 나눠주신다고 생각하시면 됩니다.

만약 filter의 크기가 커진다면 어떻게 될까요?
당연히 더 blur 현상이 일어날 것입니다. 왜냐하면 더 넓은 Spatial한 정보를 이용해서 더 blur가 되겠지요.
하지만 Convolution(Cross-Correlation입니다.)은 생각보다 많은 Computation이 들어가기 때문에 filter의 size가 커진다면 속도가 느려질 수 있습니다.

다음 그림은 Gaussian filter를 적용한 예시입니다.

Gaussian filter는 filter의 element(weight)가 distance에 따라 다르므로, 가까운 주변의 pixel들을 더 많이 참조합니다.

f(x,y) = 4라고 했을때 f(x,y-1)와의 distance는 1밖에 차이가 나지 않습니다. 그렇기 때문에 f(x,y-1) = f(x,y+1) = f(x-1,y) = f(x+1,y)값 f(x,y)와의 distance는 1이여서 모두 값이 같습니다. 그러나 조금 헷갈리는 부분이 대각선 요소입니다. 대각선 요소는 저 gaussian filter에서 element(weight)값이 1을 의미하며 f(x-1,y-1), f(x-1,y+1), f(x+1,y-1),f(x+1,y+1)을 의미합니다. 중심 좌표 f(x,y)에서 2의 distance 값을 가지게 됩니다. 그러므로 더 2보다 더 작은 값을 나타냅니다.

위 그림은 겉보기에는 box filter와 차이가 없지만, 자세히 보시면 Gaussian filter는 image의 edge를 상대적으로 보존하면서 noise를 감소시키는 것을 볼 수 있습니다. 그래서 Gaussian filter가 엣지 보존 블러링에 더 적합합니다.

box filter는 이미지가 균일하게 블러링이 되지만 엣지 정보가 크게 손실될 수 있습니다

하지만 box filter가 더 좋다는 의미는 아닙니다. 만약 단순히 블러링을 하거나 noise를 감소시키는데 필요하다면 box filter가 더 적합합니다. 그러나 엣지 보존 블러링 또는 더 정교한 결과가 필요하다면 Gaussian filter를 사용하는 것이 더 좋습니다.
box filter가 Gaussian filter보다 Computation 비용이 더 낮습니다.

~~가우시안 함수는 디지털 영상처리 기초부분에서 자세히 다루어서 여기서는 함수에 대해서 설명하지 않습니다.~~

original에서 각 filter를 적용했을때의 7x7 Gaussian filter가 box filter보다 기존의 original의 structure정보를 더 담고 있는 것을 볼 수 있습니다.
반대로 말하면 box filter는 structure 정보를 없앨 수 있게 됩니다.

Gaussian filter에 대해서 더 다뤄보겠습니다.

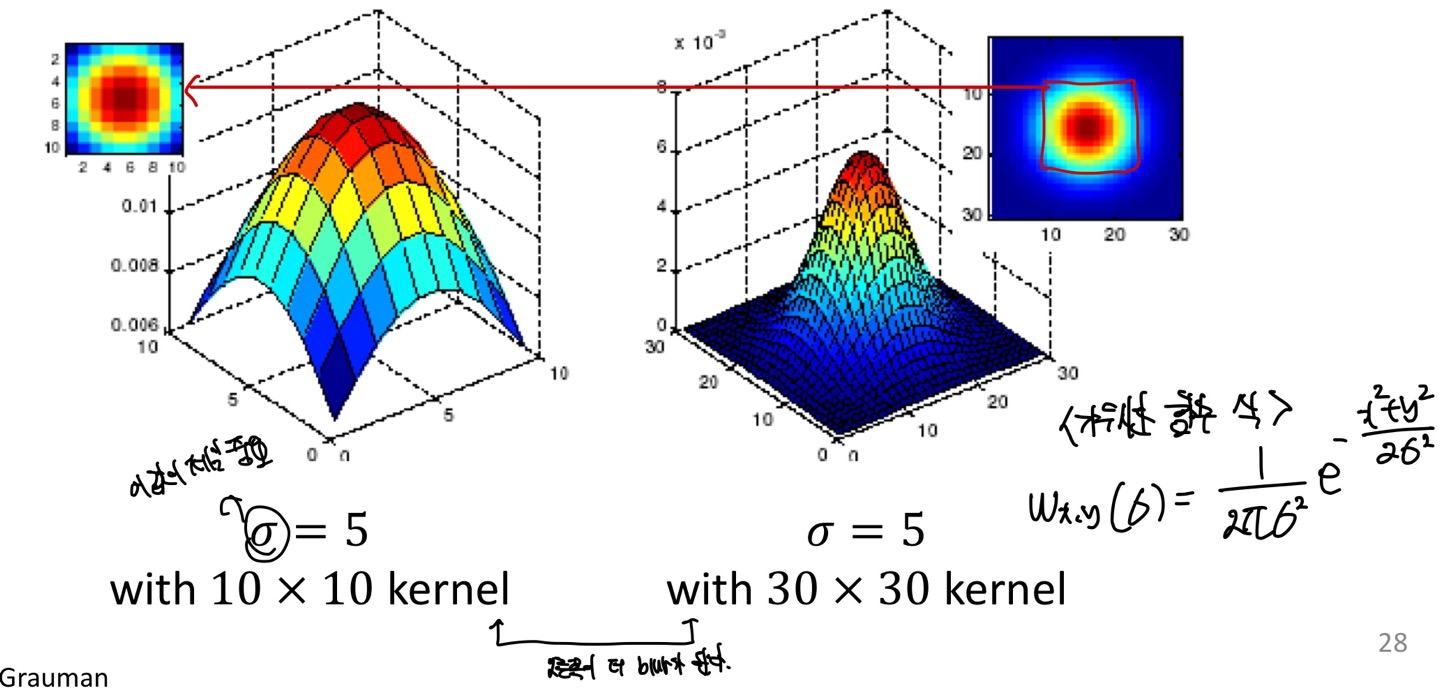
표준편차의 값이 똑같다고 했을때 filter의 size를 크게 한다면 오른쪽이 당연히 더 blur처리가 될 것입니다.
size를 키운다는 것은 주변의 내용을 얼마나 반영할지에 대한 의미로 받아들이시면 됩니다.

각 그래프를 2차원으로 보았을때, filter size가 작은 부분은 단순히 size가 큰 filter를 확대한 모습과 같습니다.

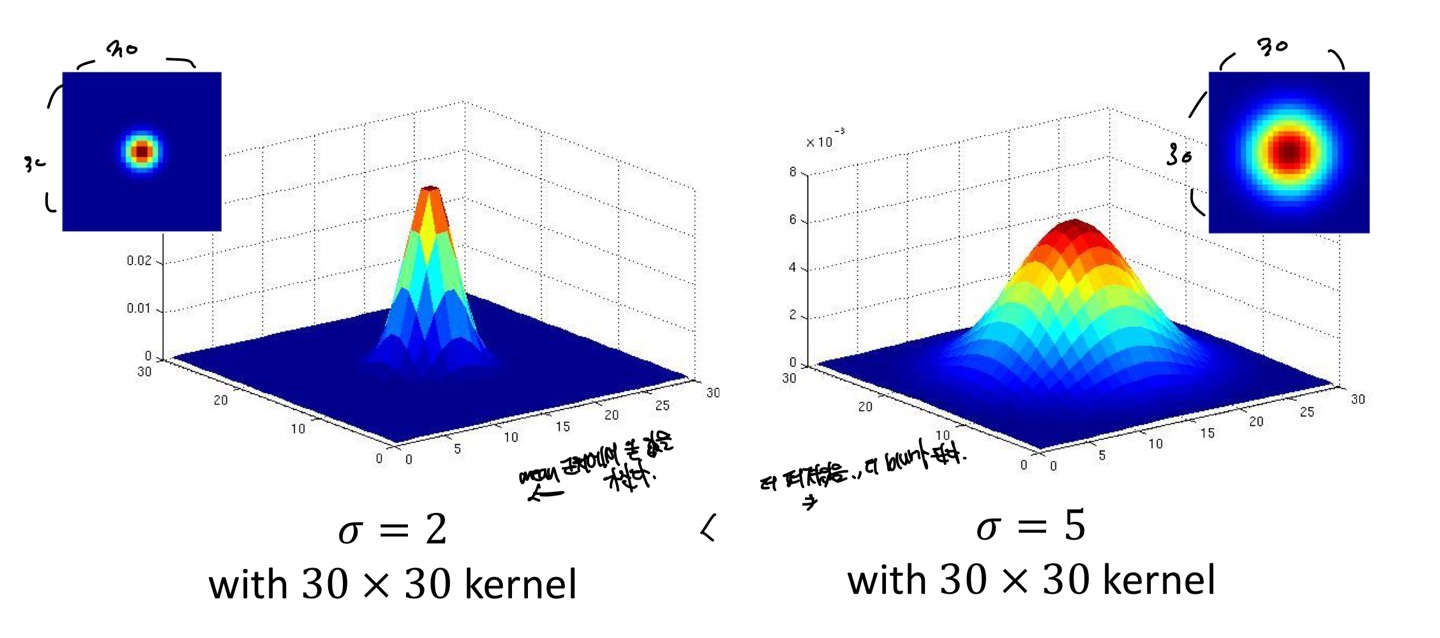
만약 그렇다면 filter size가 같고 표준편차의 크기가 다르다면 어떻게 될까요?
위의 그림에서 나와있다싶이 표준편차의 값은 Gaussian function의 봉우리의 크기를 결정하게 됩니다.
표준편차의 값이 작을수록 평균값에 더 밀집되어있고, 클수록 평균으로부터 더 멀어지는 것을 볼 수 있습니다.
표준편차의 큰 값을 Image에 적용하면 자기 자신의 pixel을 제일 많이 참조하기 때문에 blur가 표준편차의 작은 값보다 더 일어나지 않을 것 입니다.

Gaussian filter를 어떻게 설정하는 것이 가장 좋을까요?

먼저 Low-Pass filter이기 때문에 element들의 합은 1이여야합니다.
edge부근에 있는 값들은 0에 가까운 값이여야 합니다.(중심 pixel 주변의 중요한 정보에 집중하도록 하는 것)
Gaussian filter의 크기는 half-width의 크기가 3x표준편차로 설정합니다. 만약 표준편차가 1이라면 6x표준편차 + 1이 되겠네요.(이것은 경험에 의한 것이라고 합니다. 증명된 것은 없는 것 같습니다.. 아시면 댓글달아주세요.)
그렇다면 표준편차의 값이 크면 filter의 size가 커지고 작으면 size가 커진다는 의미입니다.

Properties of Convolution / Separability

Convolution의 properties는 다음과 같다.

1개의 W filter가 여러 개의 filter인 $W_1$ , $W_2$ ... $W_n$ 로 Convolution을 한 output이라고 생각해보자. 만약 f라는 image에 w라는 filter를 적용한다고 한다면 단순히 f * W로 계산을 할 수 있지만, Associative인 성질을 이용하면 f에다가 $W_1$ 을 Convolution연산을 하고, 다음 $W_2$ ... $W_N$ 으로 Convolution연산을 해도 output의 결과는 같을 것이다.

바로 위 내용을 정리한 수식은 아래와 같다.

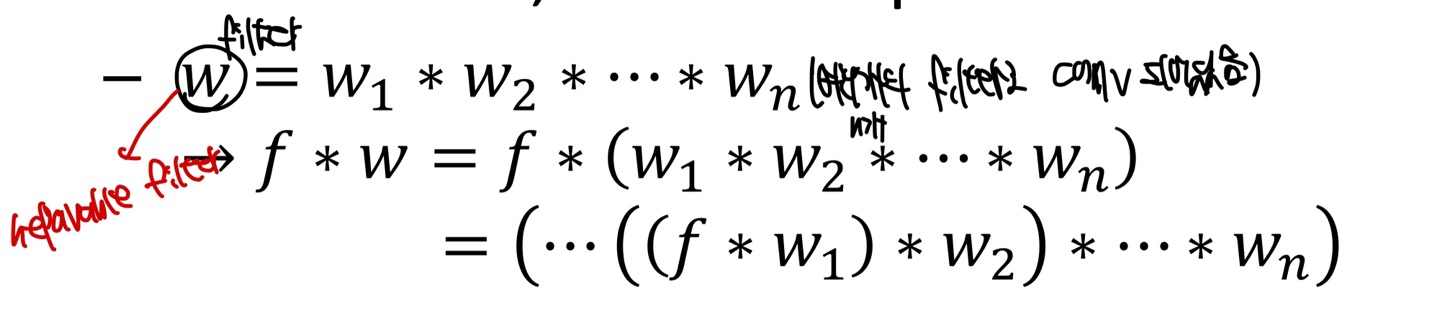
그렇다면, output의 결과가 같다면 어느것이 더 효율적일까? 이 이야기는 조금 있다가 알아보고, 먼저 2D Linear fitler가 1개의 Linear filter의 Convolution으로 이루어져있다는 것을 알아보자.

다음은 Low-Pass filter인 2D Gaussian filter가 어떻게 1D Gaussian filter로 separable로 수행이 될 수 있는지에 대한 증명과정이다.

$W_x$ 는 f image에 Horizontal로 Convolution을 적용하고, $W_y$ 는 Vertical로 Convolution을 적용한 것이다.

그렇다면 정말로 Associative성질이 맞는지 실제로 image에 적용하면서 살펴보겠다.

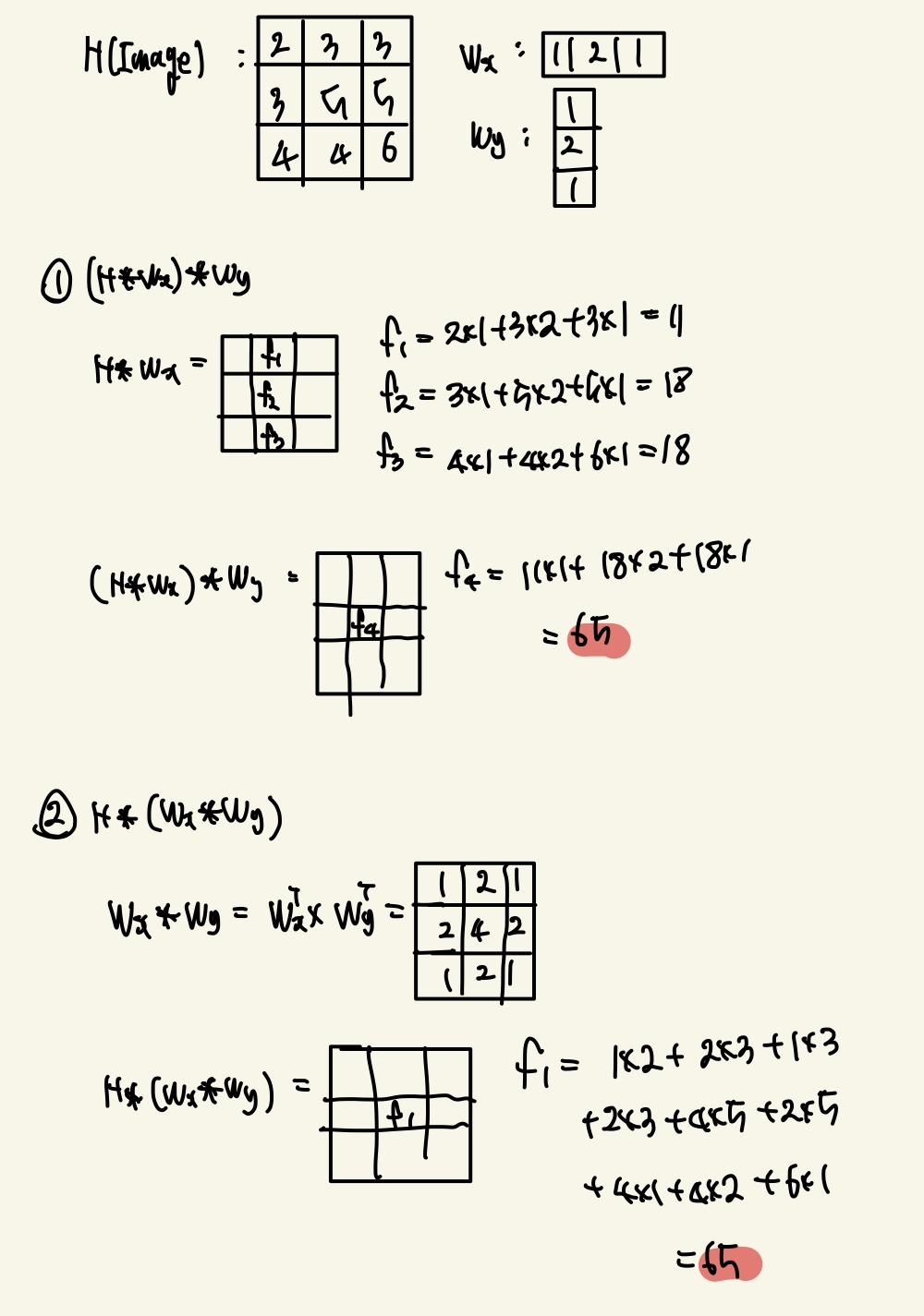
Convolution을 적용한 결과값이 1번,2번 모두 동일한 값이 나오게 되었다.

이러한 Separability는 실질적으로 Computation에 대한 이점이 존재한다.
만약 MxN의 image와 mxn의 filter가 있다고 한다면 단순히 Naive Convolution의 연산량은 O(MNmn)이 될 것이고, Separate Convolution의 연산량은 O(MN(m+n))이 될 것이다.

Nonlinear Filters

Linear filter와 Nonlinear filter의 차이
Linear filter는 Input image의 각 pixel에 대한 output pixel 값이 Input pixel 값과 Linear combination으로 계산되기 떄문에 Linearity가 유지된다.
하지만 Nonlinear filter는 Input pixel의 순서나 크기에 따라 결정되어서 Linearity가 유지되지 않습니다.

Nonlinear Filter는 새로운 Image의 Pixel값을 결정할 때, 원본 Image에서 kenel size안의 pixel중 최대/최소/중간값 등의 값으로 Pixel값을 결정한다. 대표적으로 Impulse값을 없앨때 min filter를 쓰고는 한다.
Linear filter는 새로운 Image의 Pixel값을 결정할 때, 원본 Image에는 없는 Pixel값을 할당하는 경우가 대다수이다.

Minimum filter를 적용한 첫번째 Image에서 Min filter를 적용할때의 output이 2번째 image이다.검정색으로 보이는 Noise가 pepper Noise라고 하며, 당연히 첫번째 Image에서의 Noise보다 큰 현상이 나타난다.(filter를 적용해주었기 때문이다.)
3번째 Imaeg는 salt Noise라고 불리우며 마찬가지로 Noise가 큰 현상이 나타난다.

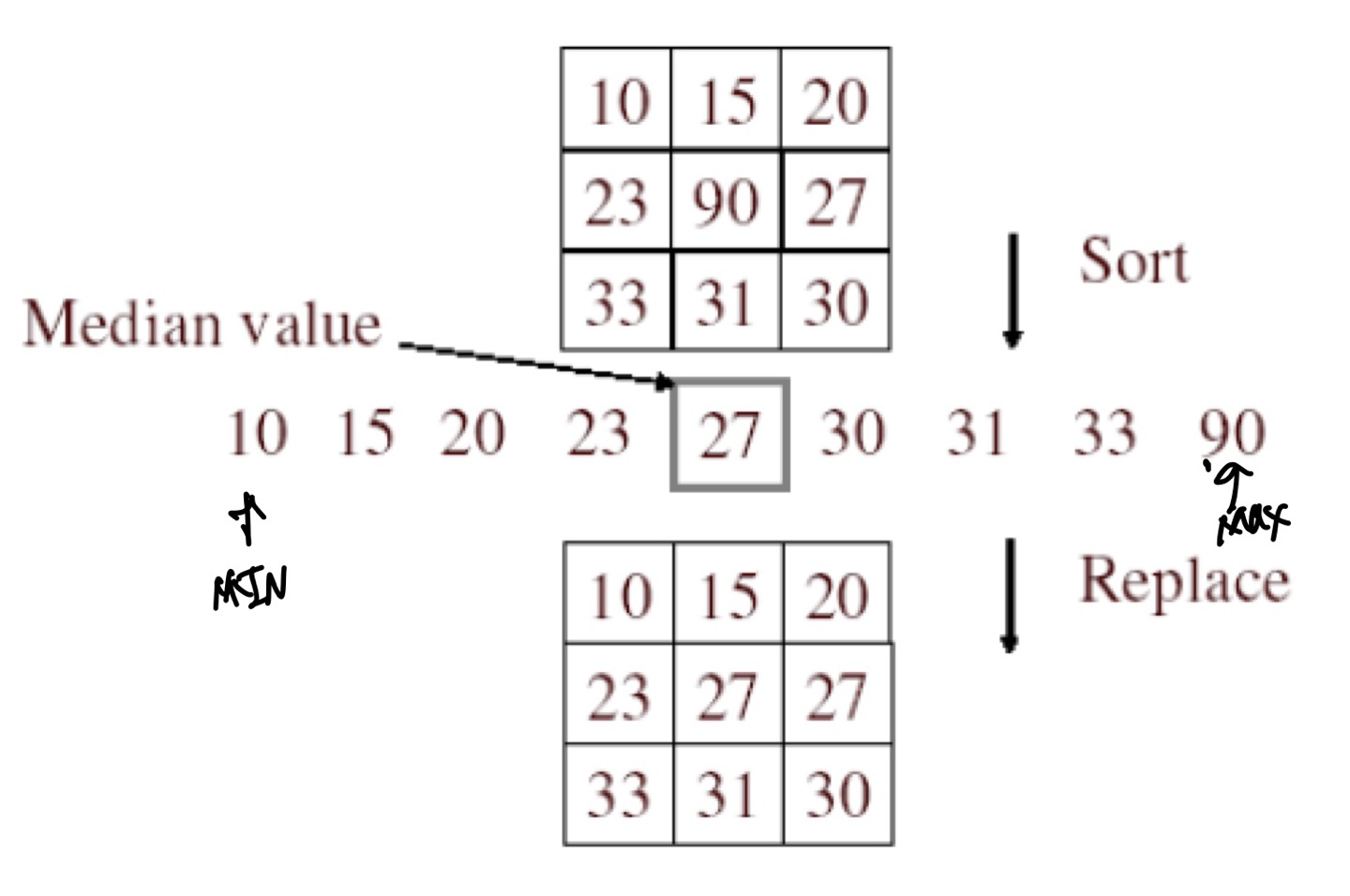
Median filter

Median filter는 중간값을 Pixel값으로 쓰는 filter를 말한다.
이 filter는 Noise(Salt & Pepper Noise)를 제거하는데 효과적이며, structure를 유지하는데에 효과적이다.

하지만 중간값을 Pixel값으로 이용하기 위해서는 여러 개의 pixel을 sorting해야하는 Computation complexity가 증가하므로, 이 complexity를 낮추기 위해 현재까지도 많은 연구들이 진행되고 있다고 한다.

Edge Detection

영상처리에서 Edge는 주변 Pixel값 변화가 급격하게 변화하는 부분을 말하는데, 이 Edge는 Image를 표현하고자 하는 Scene의 정보를 많이 표현한다.

실제로 컴퓨터비전에서 많은 업무가 Image의 Edge를 찾는것을 포함한다.

이러한 Edge는 주변의 Pixel들을 활용하는 Spatial Filtering으로 Edge를 검출할 수 있다.

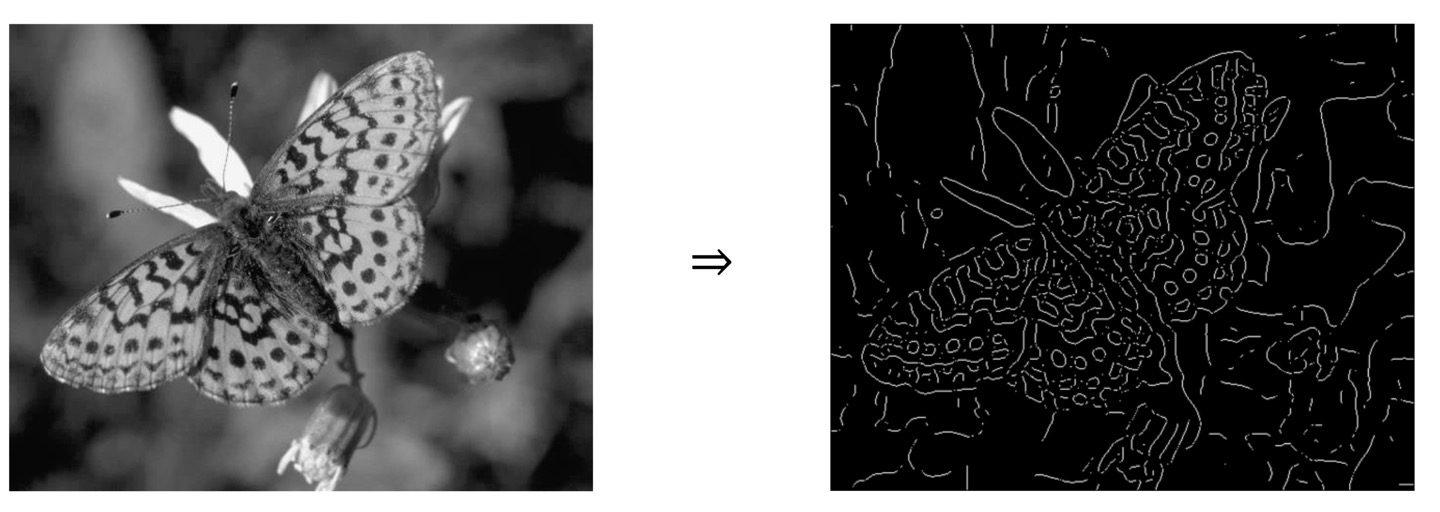
단순히 Image의 Edge를 파악하는 Algorithm을 생각해보면 Edge를 찾고자하는 Pixel이 주변 Pixel값들과 비교해서 변화량이 크다면 이 Pixel은 Edge가 된다고 생각할 수 있게 된다.

위 그림을 보게 되면, 더듬이 쪽의 흰색 부분은 주변 Pixel과의 차이가 매우 크다고 한눈에 보일 수 있다. 실제로 Edge를 검출해보면 Edge가 된다는 것을 볼 수 있다.

하지만, 이러한 주변 Pixel값들의 차이는 상대적인 값이기 때문에 이 Edge를 판별할 수 있는 척도를 우리는 배우게 된다.(Derivative, Gradient를 배우게 된다.)

What Causes an Edge?

Image에서 Edge가 생기는 이유는 Depth discontinuity, Reflectance Change, Change in Surface, Cast shadow가 있다.

Depth discontinuity는, 2개 이상의 객체 또는 표면이 서로 다른 깊이 또는 거리에 위치해 있을때 발생하게 된다. 컴퓨터비전에서 객체 분할과 깊이 정보를 추출하는데 중요한 역할을 한다.
단순히 카메라 센서와 Object의 거리라고 생각하면 되겠다.

Reflectance Change는, 빛의 반사율에 따른 변화인데 물체의 표면이 어떤 각도에서 빛을 받으면 반사율이 변할 수 있기 때문에 이 변화로 Edge가 나타나게 된다.

Change in Surface는, Object의 shape에 따라서 Edge가 생기게 된다.

Cast Shadows는, 물체가 빛을 받으면 shadow가 생기게 된다. 이러한 shadow는 Pixel값이 매우 낮으므로 주변의 Object와 Pixel값의 차이가 많이 나게 되므로 Edge 검출할 확률이 올라가게 된다.

Derivatives and Edges

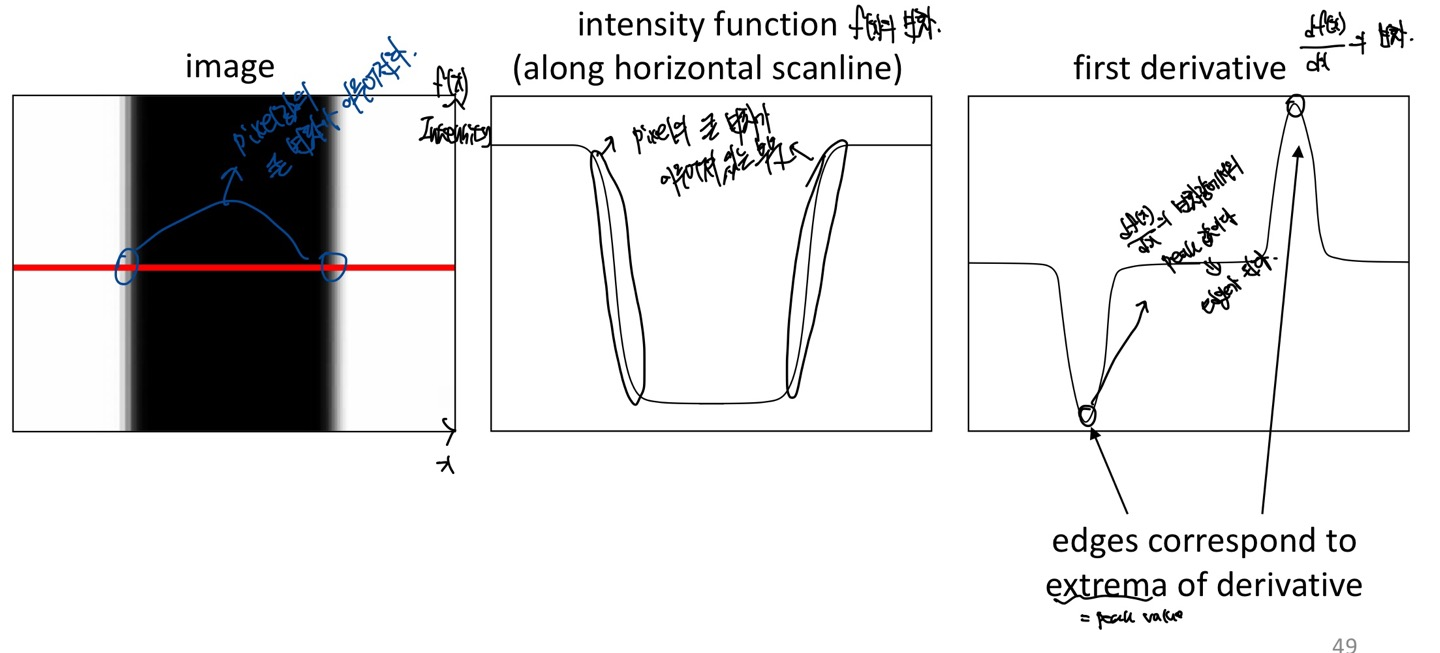
맨 왼쪽 그림을 보자. Image의 y축의 변화에 따라서 Pixel값의 변화가 없기 때문에 x축의 변화에 따라서 f(x) (Intensity)의 변화를 관찰해보는 그림이다.

빨간색의 Scanline을 통해 Pixel값을 살펴보자.

가운데 그림을 살펴보면 왼쪽의 scanline을 통한 f(x)의 변화를 그래프로 나타낸 것이다.
그래프를 살펴보면 급격하게 f(x)의 값이 변화하는 부분이 있는데, 이러한 부분이 아마 Edge로 판별이 날 것이다.

이 가운데 그림을 미분하게 되면, 좀 더 정확한 x에서 Edge를 검출할 수 있을 것이다.
왜냐하면 미분은 변화량을 나타내기 때문이다.

맨 오른쪽 그림을 살펴보면, f(x)를 미분한 그래프인데, 미분한 값이 peak값을 나타내는 것을 볼 수 있다. 그렇다면 변화량이 높은 x에서 peak값을 가지는 x를 찾을 수 있으므로 Edge를 나타내는 x, 즉 위치를 찾을 수 있게 된다

그렇다면 우리는 미분을 통해서 Edge를 찾을 수 있다는 것을 알 수 있게 되었는데, 우리는 앞에서 Spatial filtering을 통해서 Edge를 검출한다고 말했다.
이러한 미분을 어떻게 kernel로 나타낼 수 있는지 제가 직접 쓴 수식을 살펴보면 이해가 될 것 입니다.

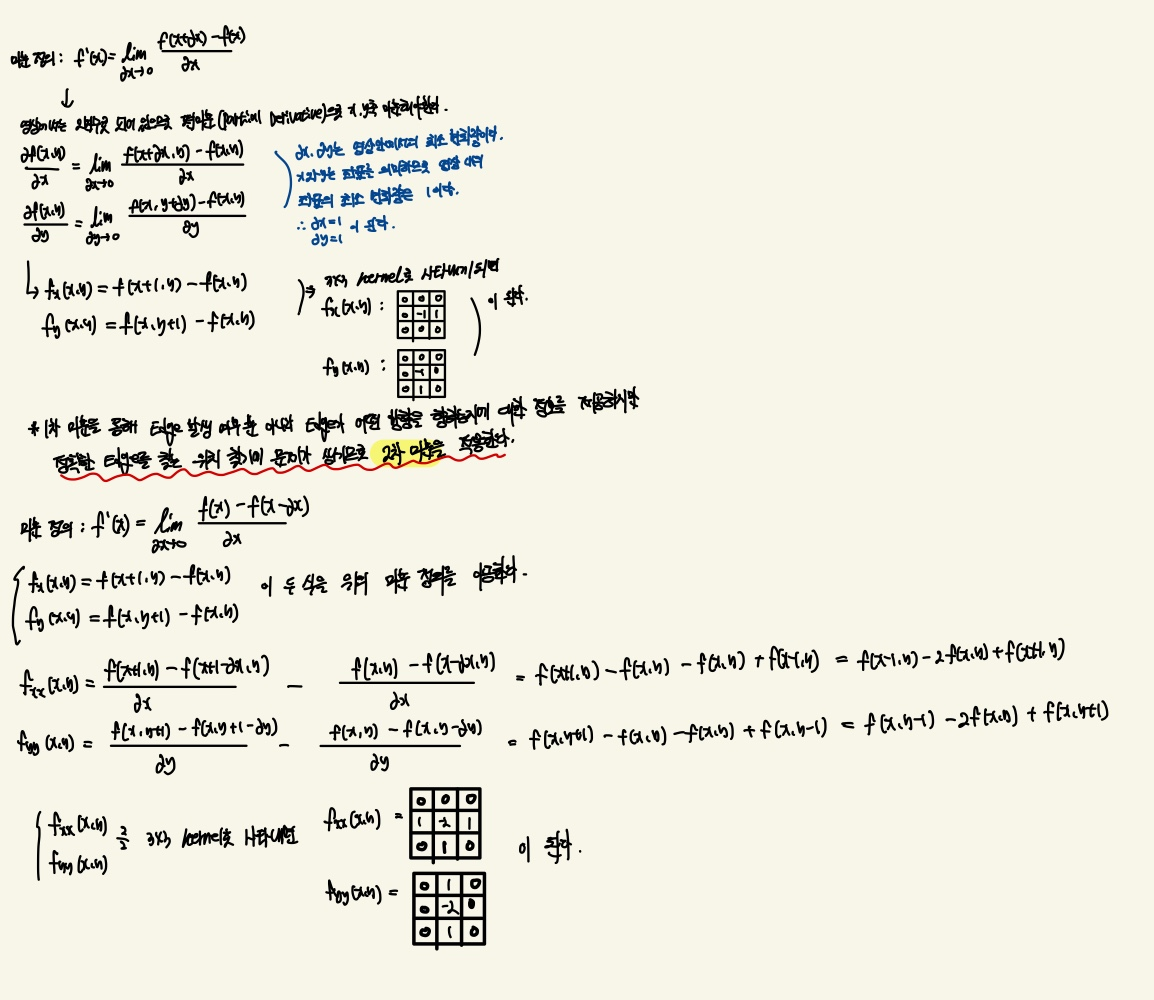
그렇다면 x축과 y축을 따로 따로 미분한 Output Image의 결과를 살펴보자

실제로 Image를 x축으로 미분을 한다는 것은 kernel을 [-1,1]로 Horizontal한 방향으로 Pixel을 계산한다는 의미이다.
하지만 Output Image를 살펴보았을때 Vertical한 Edge가 더 잘 파악되는 것을 볼 수 있다.

왜냐하면 kernel을 살펴보면 옆의 Pixel을 통해 Edge를 검출하기 때문에 Output Image에서는 Vertical한 Edge가 나올 수 밖에 없다.

Image를 y축으로 미분하면 Horizontal한 Edge가 나오는 이유는 x축으로 미분한 이유와 반대되는 이유가 되겠다.

Image Gradient

영상처리에서 Gradient는 Image의 밝기 값이 어떻게 변화하는지를 나타내는 Vector이다.

다음은 Gradient의 수식에 대한 설명을 제가 직접 쓴 것 입니다.

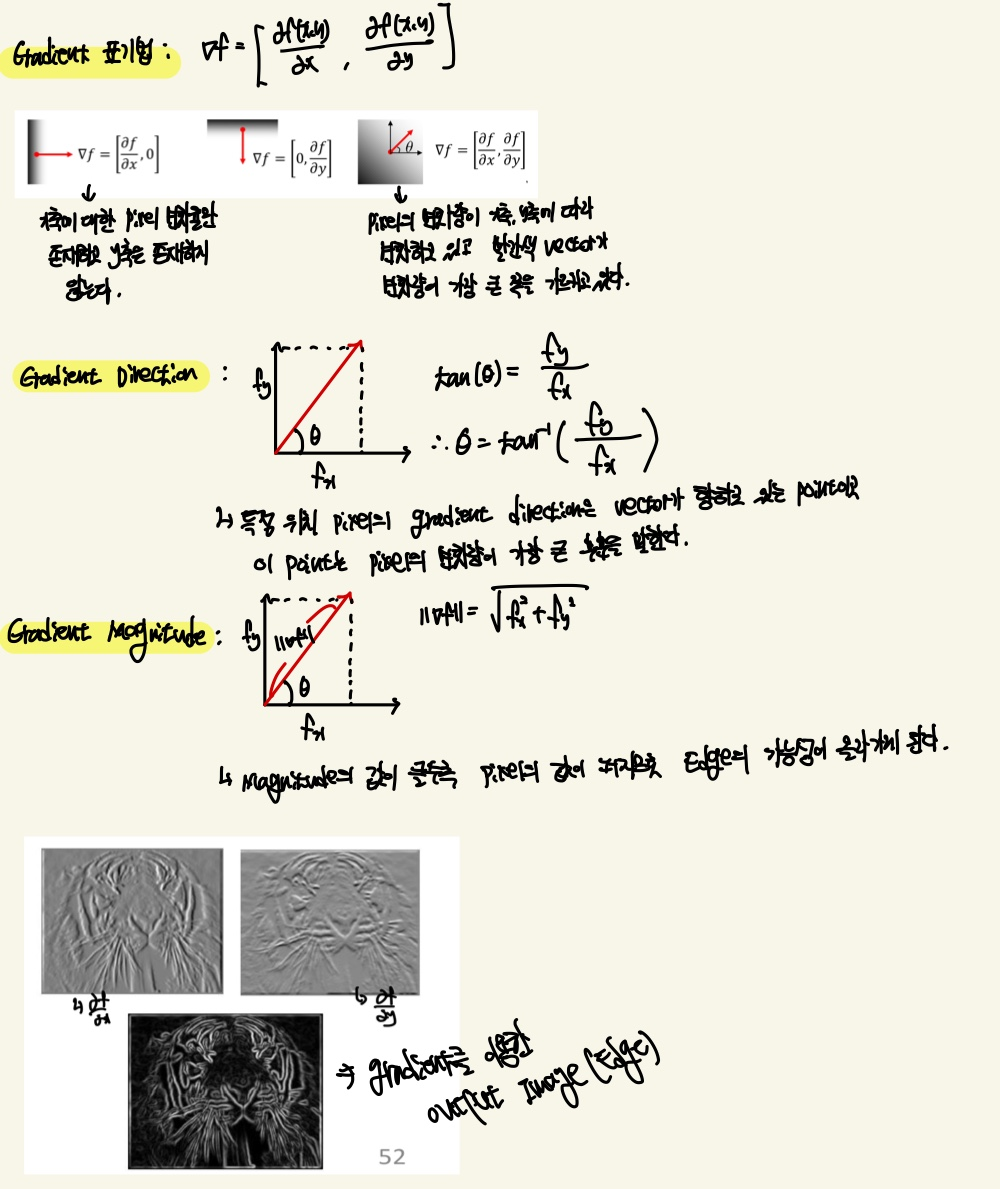
이러한 Derivative을 통한 Edge를 검출하는 filter는 Laplacian, Sobel filter등이 있습니다.

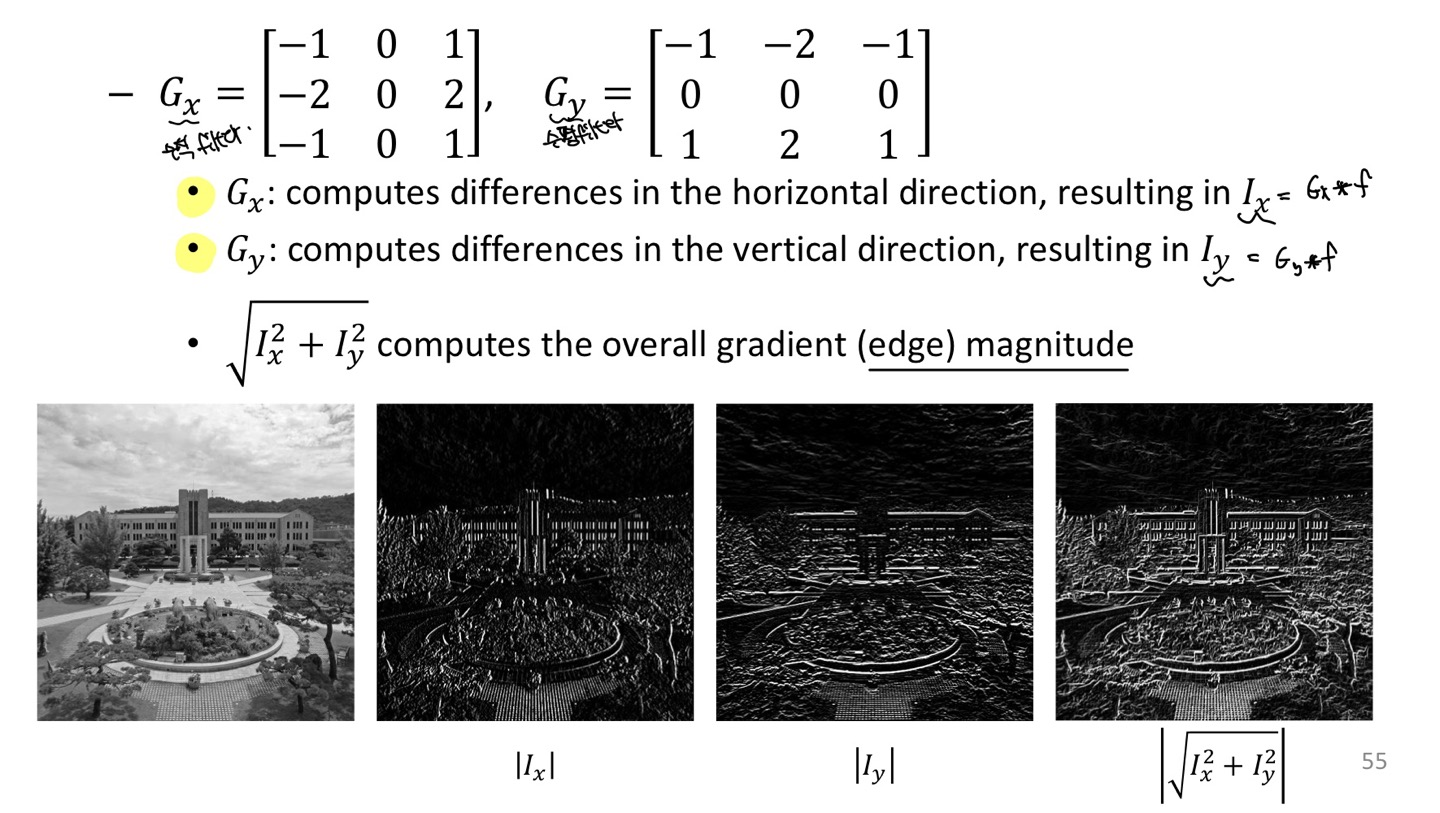
Sobel filter

Sobel연산은 Image에서 Edge를 추출하는데 대표적인 연산이고 급격한 변화가 높은 Pixel value를 비교적 평균화 시켜주기 때문에 Noise에 대체적으로 강한 특성을 보여줍니다.
그렇기 때문에 Noise가 있는 Image에서 Edge를 검출하는데 특화되어 있습니다.

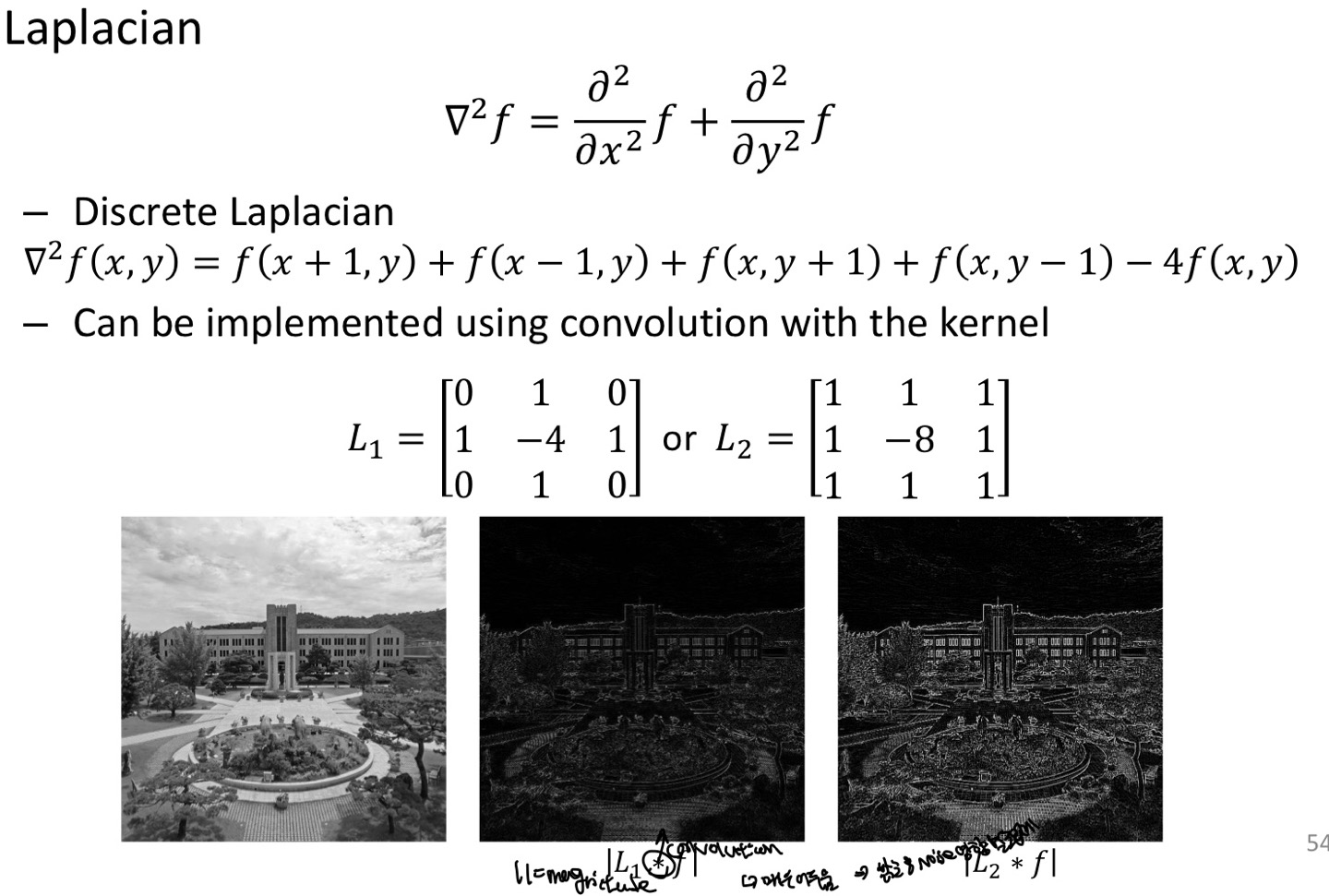
Laplacian filter

Laplacian은 sobel연산과 다르게 2차 derivative를 사용한다는 차이점이 있다.

1차 미분을 사용하는 sobel은 밝기 값이 점차적으로 변화되는 영역에서도 반응하기 때문에 상대적으로 부드러운 모양으로 Edge 검출이 가능하다.

2차 미분을 사용하는 Laplacian은 Intensity value가 점차적으로 변화되는 영역에는 반응을 보이지 않고 검출된 Edge의 윤곽선이 +에서 -로 가는 zero-crossing이 일어나서 밝기의 변화가 큰 Pixel을 찾을 수 있다.

zero-crossing이란, Pixel value의 변화가 0으로 교차하는 지점을 말한다.

다음은 sobel filter를 구현한 함수입니다.
edge를 detection하기전에 blur처리를 하는 경우가 많아서 gaussian blur를 통해 noise를 없앴습니다.

import numpy as np
import cv2 as cv
import sys

def sobel_edge(img, G_x, G_y):
    
    height, width = img.shape
    
    # == Remove Noise with Gaussian Filter before applying Sobel Filter ==
    img = cv.GaussianBlur(img, (3, 3), 0)
    
    # Each x,y Output Define
    filtered_G_x = np.zeros_like(img, dtype=np.float32) # Horizontal Detection 
    filtered_G_y = np.zeros_like(img, dtype=np.float32) # Vertical Detection
    
    # Edge detection Calculate (가장자리는 뺏음)
    for y in range(1, height - 1):
        for x in range(1, width - 1):
            
            pixel = img[y - 1 : y + 2, x - 1 : x + 2] # Get surrounding pixel values
            
            filtered_G_x[y, x] = np.sum(G_x * pixel)
            filtered_G_y[y, x] = np.sum(G_y * pixel)
    
    # Overall Gradient Edge Magnitude
    edge_magnitude = np.sqrt(filtered_G_x ** 2 + filtered_G_y ** 2)
    edge_magnitude = np.floor(edge_magnitude).astype(np.uint8)
    
    return edge_magnitude

img = cv.imread('dgu_gray.png', 0)

if img is None:
    sys.exit('Unable to read file')

G_x = np.array([[-1, 0, 1],
                [-2, 0, 2],
                [-1, 0, 1]])    
    
G_y = np.array([[-1, -2, -1],
                [0, 0, 0],
                [1, 2, 1]])

out_img = sobel_edge(img, G_x, G_y)

cv.imshow('input_image', img)
cv.imshow('output_image', out_img)
cv.waitKey(0)
cv.destroyAllWindows()  # Close all OpenCV windows