신호란 무엇인가?
신호는 정보를 표현하기 위한 변화의 패턴인데 이때의 변화는 시간 상의 변화 또는 공간상의 변화를 뜻한다.
신호처리는 시간 상의 변화를 주로 다룰 예정이기 때문에 공간상의 변화는 아주 짧게 설명하겠다.
시간 상의 패턴을 보이는 신호를 우리는 시계열 혹은 시간 신호라고 한다. 여기에서 패턴은 함수(Function)과 비슷한 의미를 지닌다. 예를들어 설명하자면, 패턴은 어떠한 입력값이 주어졌을때의 출력값을 나오게끔 해주는 의미로 해석하면 된다.
그렇다면, 우리는 신호가 시간에 대한 함수라는 관점에서 s(t)로 표현이 가능하다.
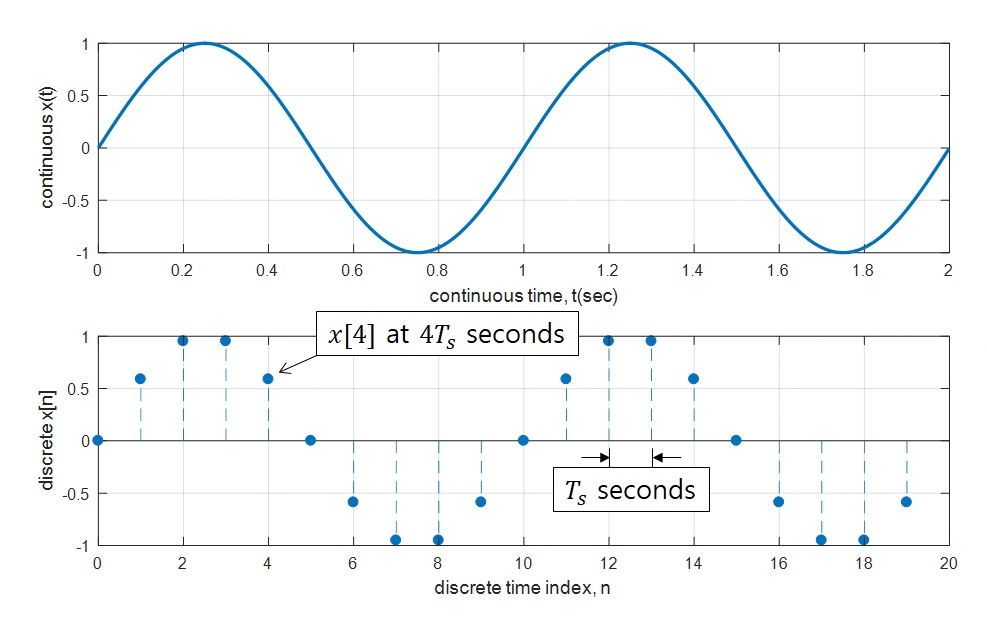
위의 그림을 보면 시간(t)에 따라서 신호가 2가지로 나뉘는 것을 알 수 있다.
시간신호는 Continuous신호(연속 신호)와 Discrete신호(이산 신호)로 나뉘어지게 된다.
Continuous신호는 수학적으로 표현하면 실함수로 표현이 가능하며, 대표적으로 Analog신호가 존재한다.
Discrete신호는 Continuous신호를 Sampling한 신호로 함수로 표기할때는 중괄호인 [ ] 을 쓰게 된다. Continuous는 ( )를 쓴다.( 연속 신호: s(t), 이산 신호 : s[t])
당연히 우리는 이산 신호를 배울 가치를 못느낄 수 있다. 하지만 디지털기기에서 연속과 무한이라는 개념을 표현하지 못하기 때문에 이산적으로 나열한 수열을 가지고 모든 신호가 표현된다.
시간이 아닌 공간 상 변화하는 패턴을 보이는 신호도 있는데 이러한 예시는 Image에서 볼 수 있다.
시스템이란 무엇인가?
시스템은 새로운 신호 or 다른 신호 표현으로 변화시키는 함수이다.("패턴을 바꾼다"라는 표현이 옳바를거같다.) 즉, 어떠한 입력신호에서 출력신호로 변환할때 어떠한 함수를 통해 변환이 될 것 이다. 이러한 변환은 시스템이 역할을 맡게 된다.
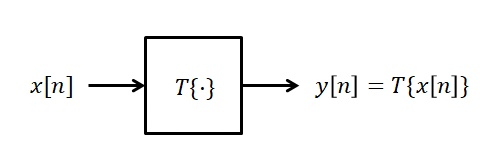
위의 T가 변환을 의미한다.(Transformation)
시스템은 입력/출력의 종류에 따라서 시스템의 종류를 구분하게 된다.
- 연속 시간 시스템 : 입/출력이 모두 연속 시간 신호
- 이산 시스템 : 입/출력이 모두 이산 신호
- Analog-Digital-Converter System : 입력 : 연속 시간 신호, 출력 : 이산 신호
- Digital-Analog-Converter System : 입력 : 이산 신호, 출력 : 연속 시간 신호
신호처리와 선형대수학과의 연결성
우리는 앞서 T(Transformation)을 통해서 출력값을 변형 시킨다고 하였다.
이러한 T는 선형대수학에서 배우는 Matrix를 통해 Linear Transformation으로 변환 시킨다는 개념과 똑같다.
조금 더 알아보자.
신호와 시스템은 선형대수학에서 Vector와 Matrix 개념에 대응 가능하다.
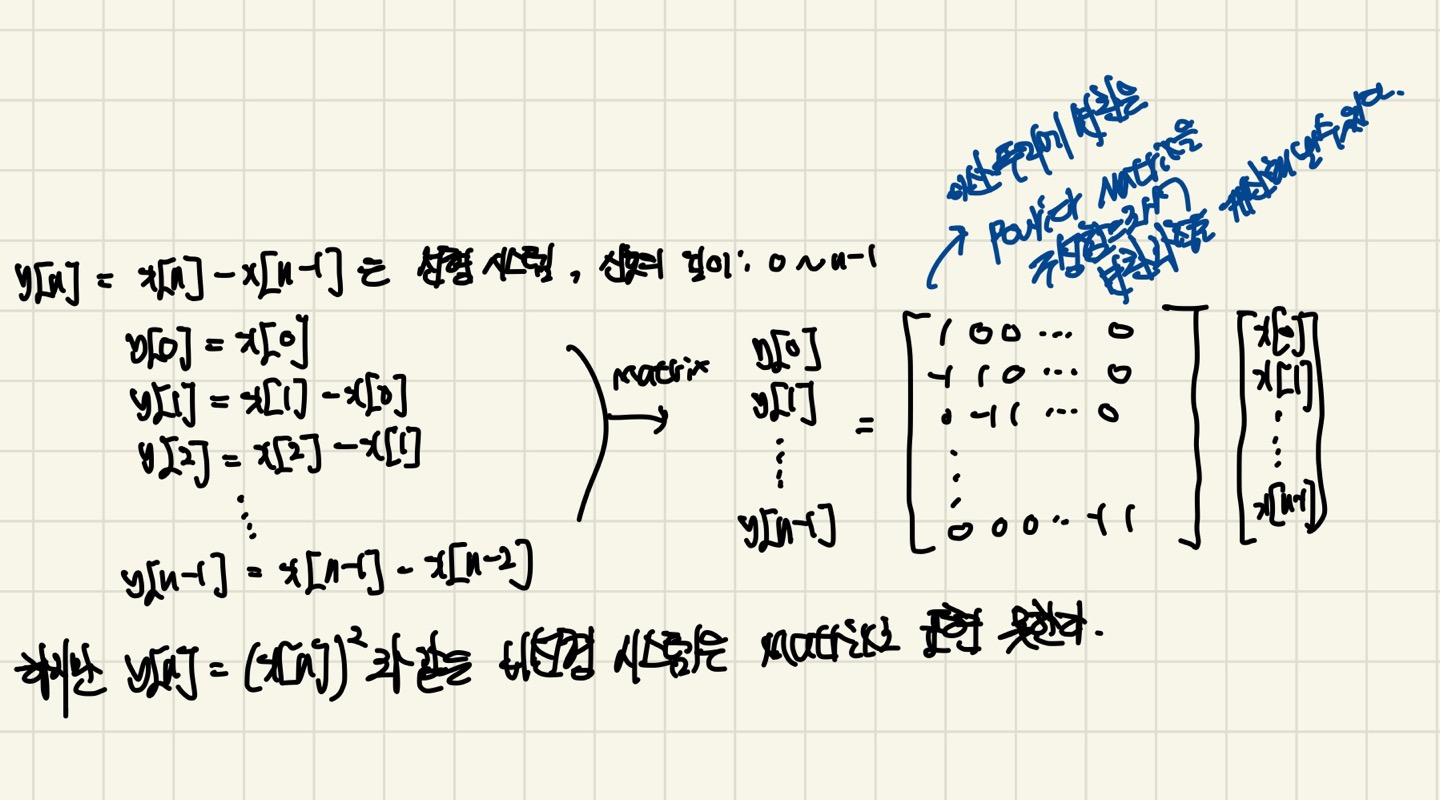
디지털 기기에서는 신호를 Column Vector로 표기하게 되고 system은 무조건 Linear해야한다.(신호처리가 Linear한 Transformation을 다루는 것이다.)
그림으로 한번에 설명하면 다음과 같다.
정현파(Sinusoidal Wave)의 기초
푸리에 분석에 따른 결론은 결국 신호는 정현파의 합으로 표현이 가능하다 라고 결론이 났다.
정현파는 우리가 중학교때 배운 Sin과 Cos을 총칭하는 단어이다.
우리는 Sin,Cos이 왜 그러한 주기를 가지고 주파수를 가지는지 정확하게 잘 모른다.
정현파의 본질은 원 위의 회전에 관한 것 이다.(회전의 방향은 반시계 방향을 양의 방향으로 봅니다.) 그리고 시간에 따른 회전을 기술한 것이다.
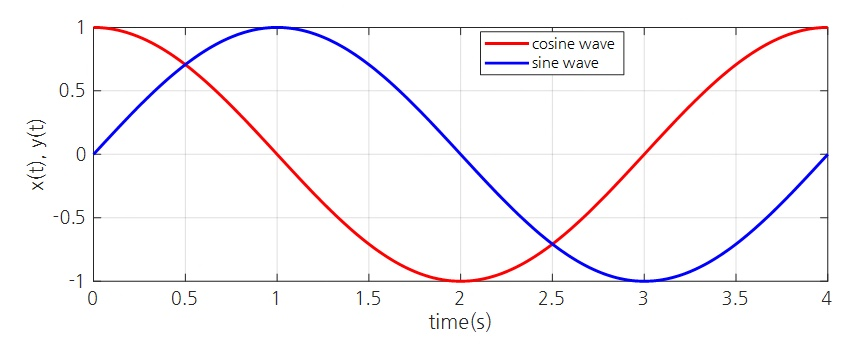
조금 더 자세히 말하자면, 원은 2차원 평면상으로 충분히 그릴 수 있다. 하지만 정현파는 시간에 따른 원을 기술한 거기 때문에 2차원에서 시간 t의 축을 그릴 수 없기 때문에 x축이나 y축 둘 중의 1개를 포기해야하는 상황이 왔다.
그렇기 때문에 원에서 x축의 변화만으로 그린 그래프가 Cos이고, y축의 변화만으로 그린 그래프가 Sin이 된다.
정현파(Sinusoidal Wave)의 3가지 특성 값
우리는 원에다가 장난을 치고 싶다. 우리는 장난을 원의 반지름, 회전 속도, 회전하기 시작한 곳의 위치 조절이 가능하다.
이때 원의 반지름은 진폭(Amplitude), 회전 속도(Frequency), 회전하기 시작한 곳의 위치(Phase Shift)로 장난을 칠 수 있다.
이러한 장난을 Sin, Cos에 덧붙혀넣어서 수식을 공식화 할 수 있는데, 다음은 Cos만을 기준으로 공식을 작성한 것이다.(Sin도 똑같이 공식화 됩니다.)
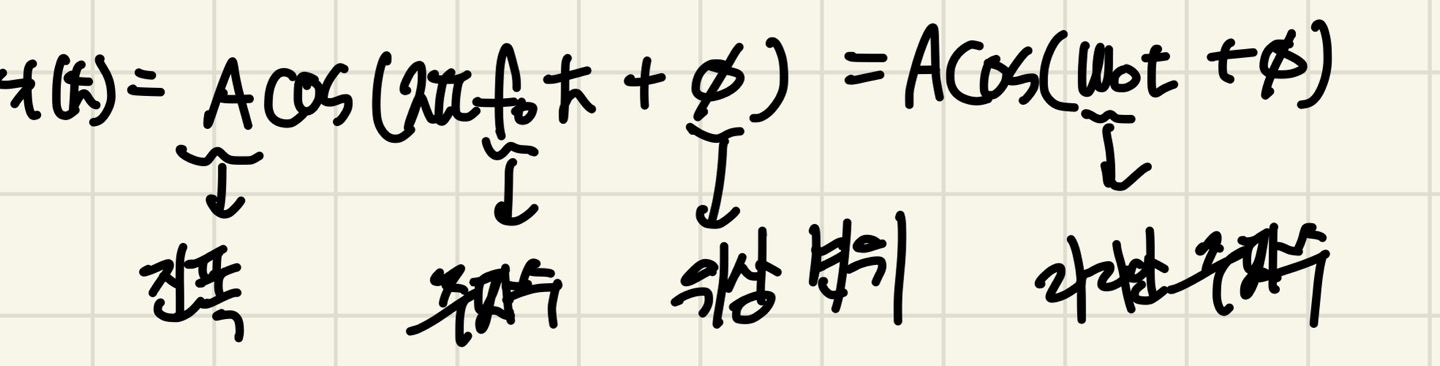
위의 3가지 특성으로 진폭, 주파수, 위상변위를 살펴보겠습니다.(라디안 주파수는 주파수에서 설명합니다.)
진폭(Amplitude)
-
회전하는 원의 반지름과 같습니다.
-
진폭 A의 값이 클수록 원의 반지름은 크고 작을수록 원의 반지름은 작습니다.
주파수(Frequency)
-
회전 속도와 관련 있습니다.
-
빨리 회전할 수록 주파수의 값은 높고 느리게 회전할 수록 주파수의 값은 작습니다.
-
주파수 =
-
단위 = HZ로 표현한다.
EX) 0.25HZ : 4초에 1번 회전, 1HZ : 1초에 1번 회전, 2HZ : 1초에 2번 회전
만약 1번 회전하는데 얼마나 걸리는지 알려면, 로 공식화 할 수 있다.
라디안 주파수(Radian Frequency)
-
라디안 각도체계는 원을 1번 회전할 때 반지름과 길이의 비율이 항상 2pi임을 고려해 만든 각도 체계입니다.
-
라디안 주파수는 1초에 몇 라디안을 회전하는지를 파악하려고 만든 개념입니다.(결국 각도를 계산한다.)
-
2pi rad/s의 라디안 주파수는 1초에 1번 회전한 것입니다.
-
w = 2pi x f로 표현합니다.
위상 변이(Phase Shift)
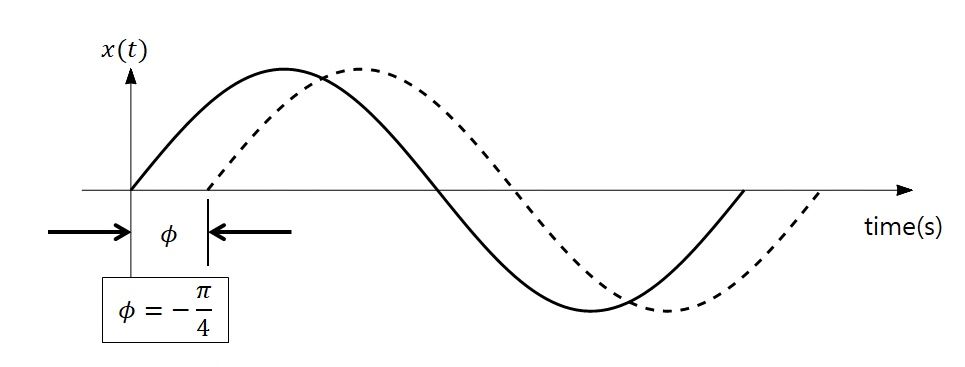
-
위상 변이가 되면 정현파가 좌/우로 옮겨지게 됩니다.
-
'위상'은 원의 어디서부터 출발 할건지를 말해줍니다.
-
ϕ : 회전을 시작하는 위치입니다.
중요 성질은 제가 직접 설명했습니다.

복소수 표현 방법
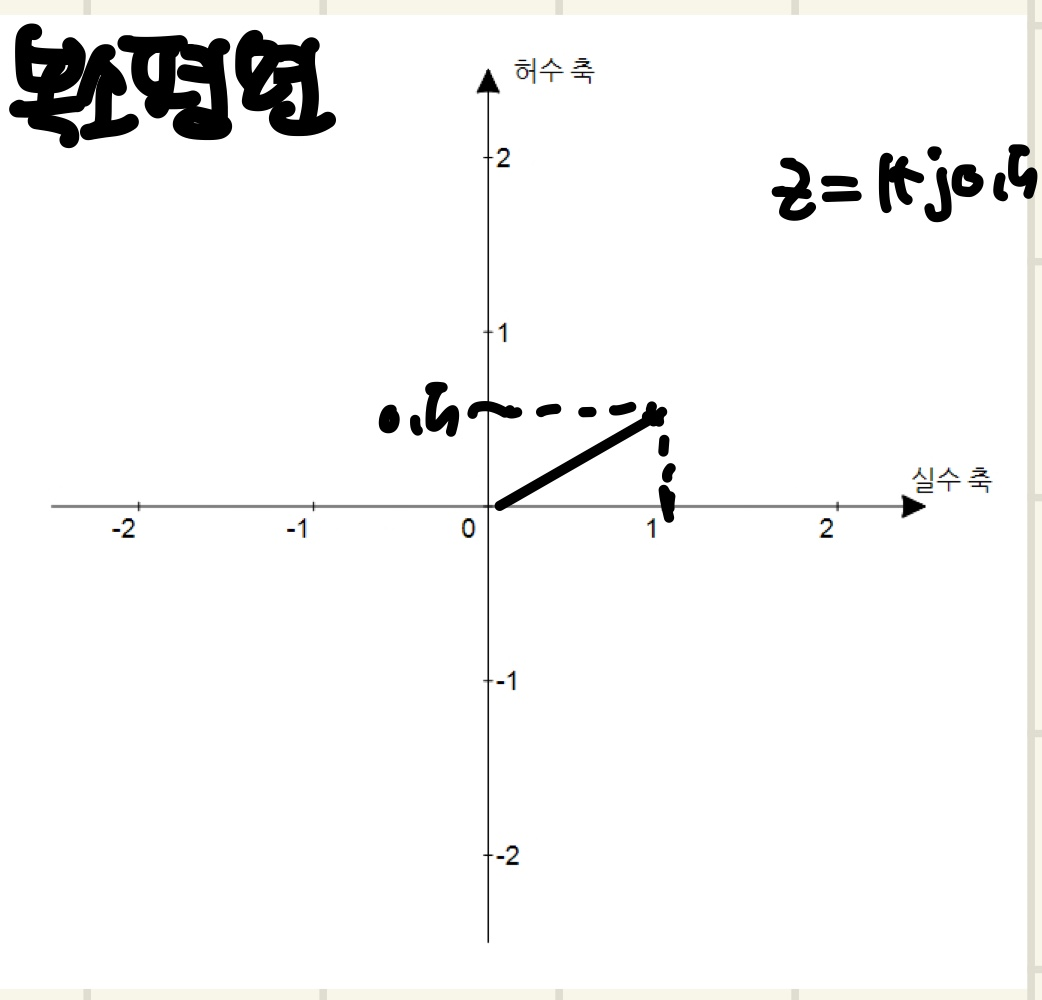
허수 축은 실수 축에 직교하는 수 체계이다. 직교하면 내적이 생각나야하는데, 허수와 실수를 내적하면 0이 된다는 것은 머리에 있으시면 좋겠습니다.
복소수는 실수부와 허수부로 표현할 수 있는데, 직교 좌표계 or 극 좌표계 둘 중 아무거나 사용해도 복소수를 표현할 수 있습니다.
직교 좌표계(Cartesian Coordinate)
우리가 처음으로 좌표계를 배우는 x축,y축으로 표현하는 좌표계 입니다.
직교 좌표계는 복소수를 실수부와 허수부로 나누어 표현할 수 있습니다. 예를 들자면 (2,3)이라는 x축점과 y축점이 있다면 복소수로 2+j3으로 표현할 수 있습니다.
따라서 x좌표와 y좌표를 통해서 "x+jy"의 복소수를 표현할 수 있습니다.
극 좌표계(Polar Coordinate)
극 좌표계는 복소수를 원점으로부터의 거리와 가로축에서부터의 각도를 이용해 표현하는 것을 의미합니다.
만약 직교 좌표계에서 (x,y)의 좌표계가 있다면 r은 빗변의 길이를 의미하게 되므로 피타고라스의 정리를 써주면 됩니다.
각도는 우리가 잘알고 있는 arctan()로 표현해주면 됩니다.
다음은 위의 설명을 풀은 내용입니다.
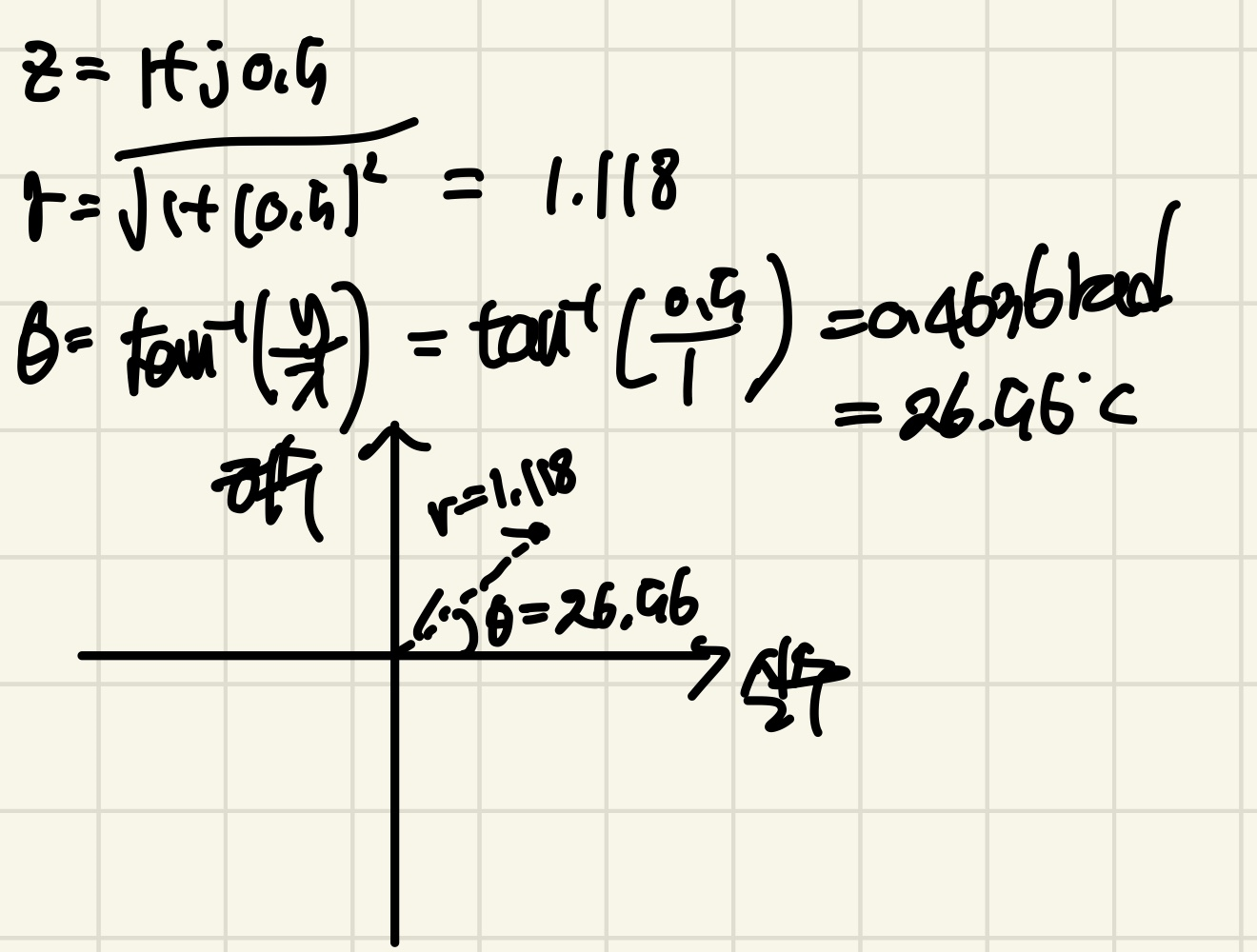
복소수는 회전과 관련이 있는 수체계입니다. 그래서 회전을 표현하는데 있어 극좌표계를 이용하면 간략하게 표기를 할 수 있고 곱셈과 나눗셈의 연산을 손쉽게 할 수 있다는 장점이 존재합니다.
따라서, 정현파는 원의 회전에서 시작한 개념이기 때문에 회전에 더 적합한 극좌표계를 더 많이 사용합니다.
점을 표현할때는 (r,θ)로 순서쌍으로 표현할 수 있는데, r∠θ로도 표현이 가능합니다.
r은 원점으로부터의 거리이고, θ는 각도를 의미합니다.
이떄 θ는 -pi<θ<pi로 표현이 되며 (3, 280)이면 280 - 360을 해주어 (3,-80)으로 바꿔서 볼 수 있습니다.
(3, -190)이면 -190 + 360을 통해서 (3, 170)으로 표현해주시면 됩니다.
직교 좌표계와 극 좌표계의 변환
극 좌표계 -> 직교 좌표계
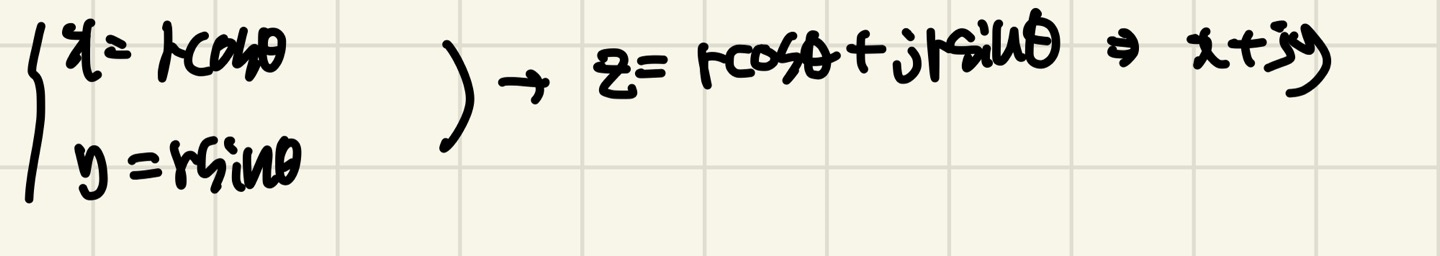
직교 좌표계 -> 극 좌표계
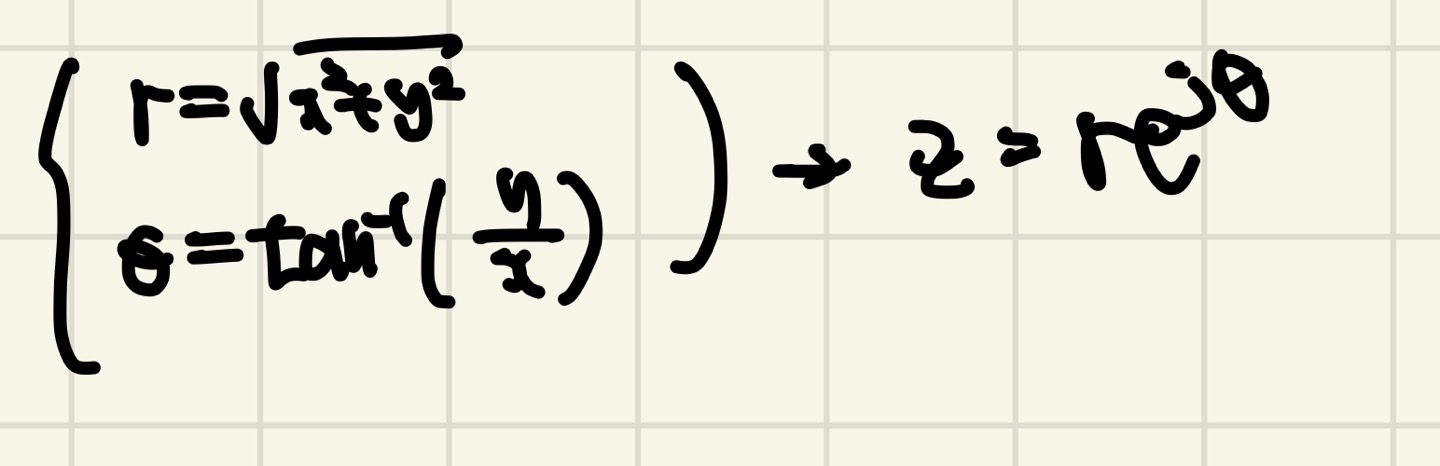
오일러 공식
오일러 공식은 공학도라면 무조건 알아야하고 무엇을 의미하는지 알야아 할 필요가 있습니다.
앞선, 극 좌표계에서 점을 표현하는데 사용이 되므로 유도 과정을 잘 살펴보시길 바랍니다.

이를 통해 극 좌표계의 표현 방법을 복소 지수를 이용해 표현할 수 있게 되므로 복소수간 곱셈과 나눗셈이 편해집니다.
복소수의 사칙 연산
복소수의 기본적인 사칙 연산을 나타냈습니다.
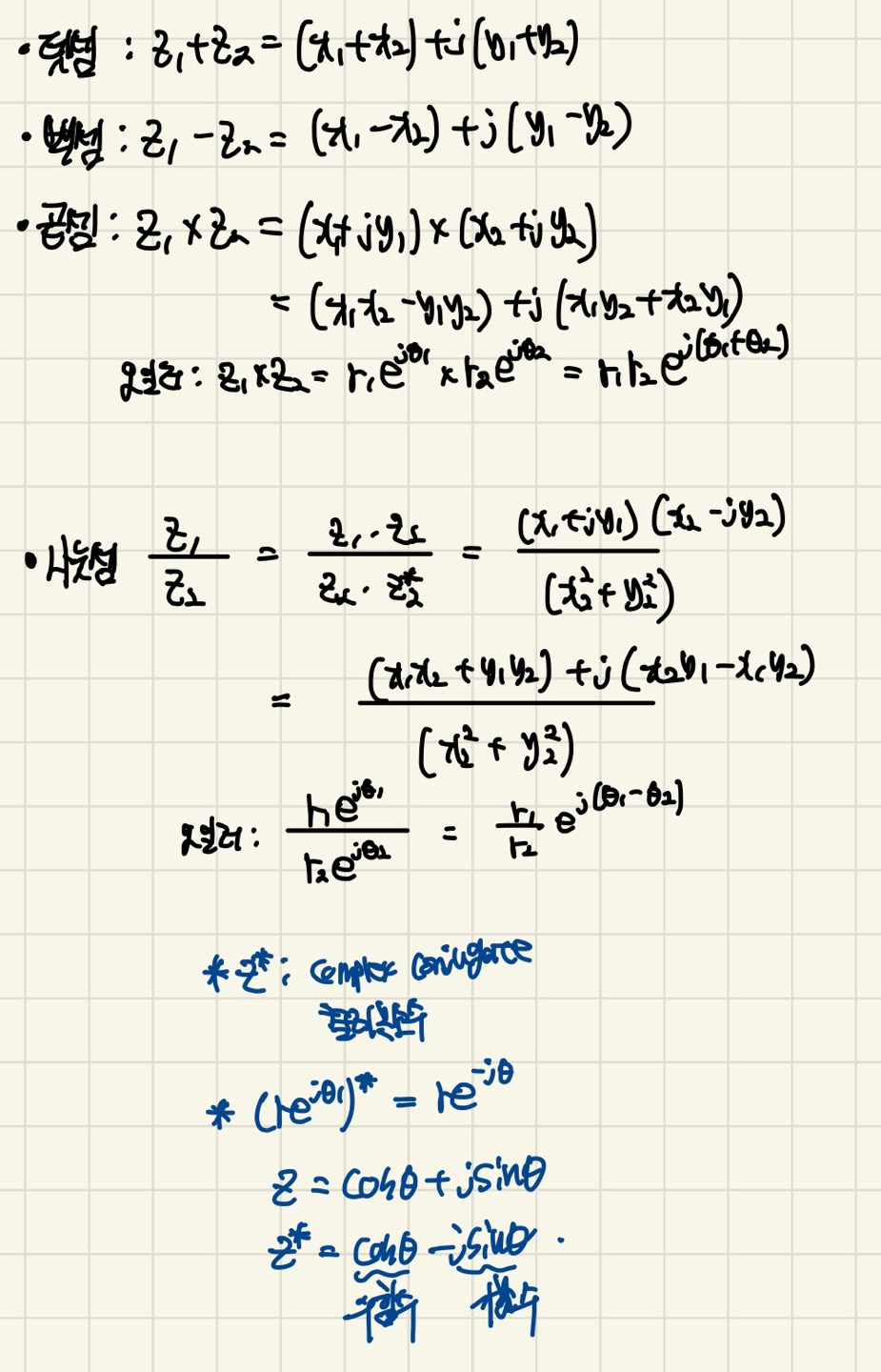
보시는 것처럼 실수의 범위로 곱셈과 나눗셈을 계산하게 되면 매우 복잡하다는 것을 알 수 있습니다. 하지만 오일러 공식을 활용해서 계산하면 매우 빠르게 계산하는 것을 볼 수 있습니다.

