우리는 Image를 sampling하여 discrete한 값(pixel)을 얻게 된다.
이러한 discrete한 값에서 time domain에서 frequency domain으로 변경하는 것을 DFT(Discrete Fourier Transform)이라고 한다.

그렇다면 우리는 DFT를 왜 배울까?
앞서 말했다싶이 frequency domain으로 Image를 변환시킬 수 있다.
이것은 frequency 성능을 분석하는데 유용하며, frequency domain에서의 정보를 활용하여 신호나 영상을 처리하거나 해석할 수 있게 된다.

또한 filtering이 가능하여 frequency성분을 제거하거나 강조하여 noise를 제거하거나 특정 패턴을 감지하는데 사용할 수 있다.

즉, time domain에서 보이지 않던 특정 패턴이나 noise가 frequency domain에서는 보일 수도 있다.

---

DFT 수식

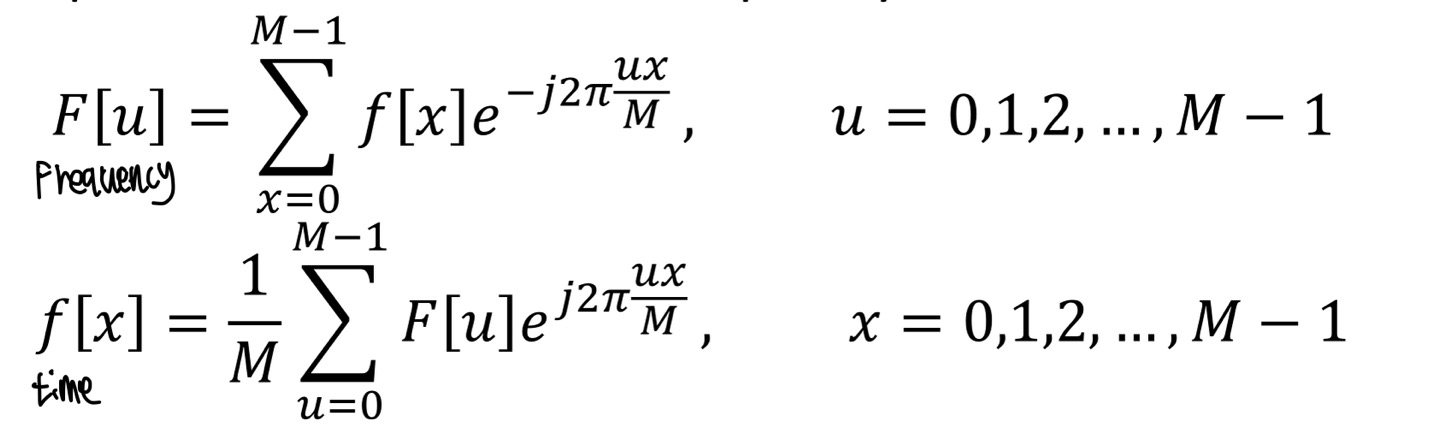
F[u]는 f[x]의 time domain의 값을 frequency domain으로 변환하는 수식이다. f[x]는 F[u]와 반대이다.

F[u]의 수식을 해석하자면, fx라는 유한한 값이 존재할때, 각 frequency를 M개로 쪼갠 후 u번째 frequency에 해당하는 변환값을 찾아내는 것이다.
$\frac{1}{M}$은 Forward transform 또는 inverse transform에 적용 가능하고, $1\over \sqrt {M}$을 각각 분배해줘도 상관 없다.

F[u]를 $F_u$, F{f(x)}
f[x]를 $f_x$, $F^{-1}${F[u]}
로 표기할 수 있다.

F[u]와 f[x] 모두 M개의 element를 가지는 signal이며, 주기가 M인 periodic signal이 된다. 일반적으로 1개의 period만 사용한다.

---

Reversible Transform

DFT는 reversible한 transform이다.

다음과 같은 과정을 통해서 증명할 수 있다.
phasor의 대한 기본개념이 잡혀있으면 이해하는데 어려움이 없을 것이다.

---

Matrix representation

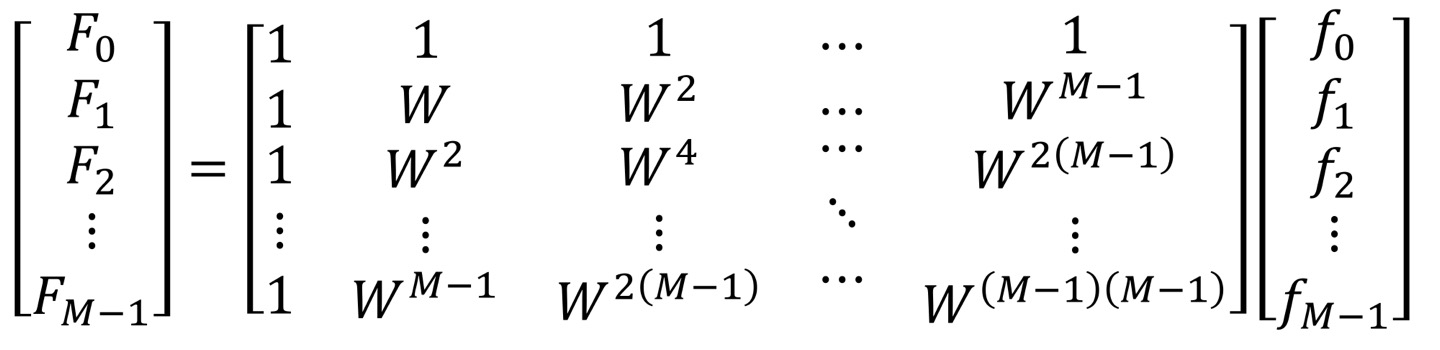
Matrix로 표현하게 되면 단순히 Ax = b로 Linear Equation으로 표현할 수 있으며, 선형대수학과 밀접한 관련이 있음을 보여준다.

forward trasnform일때는 w = $e^{-j2pi/M}$으로 나타내면 된다.
inverse transform일때는 exponential에 -(마이너스)값만 빼면 되고, F와 f만을 서로 바꿔주면 된다.

간단한 예시를 들어보겠습니다.

M = 2이라고 하자.
그렇다면 w = $e^{-jpi}$가 되고 이것을 오일러 법칙으로 변환하면 cos(pi)가 되므로 -1값이 된다.(forward는 -1이고 inverse는 $e^{jpi}$이므로 cos(pi)로 -1이다.)
위에 있는 Linear Equation방법으로 풀게 된다면 forward와 inverse는 다음과 같다.

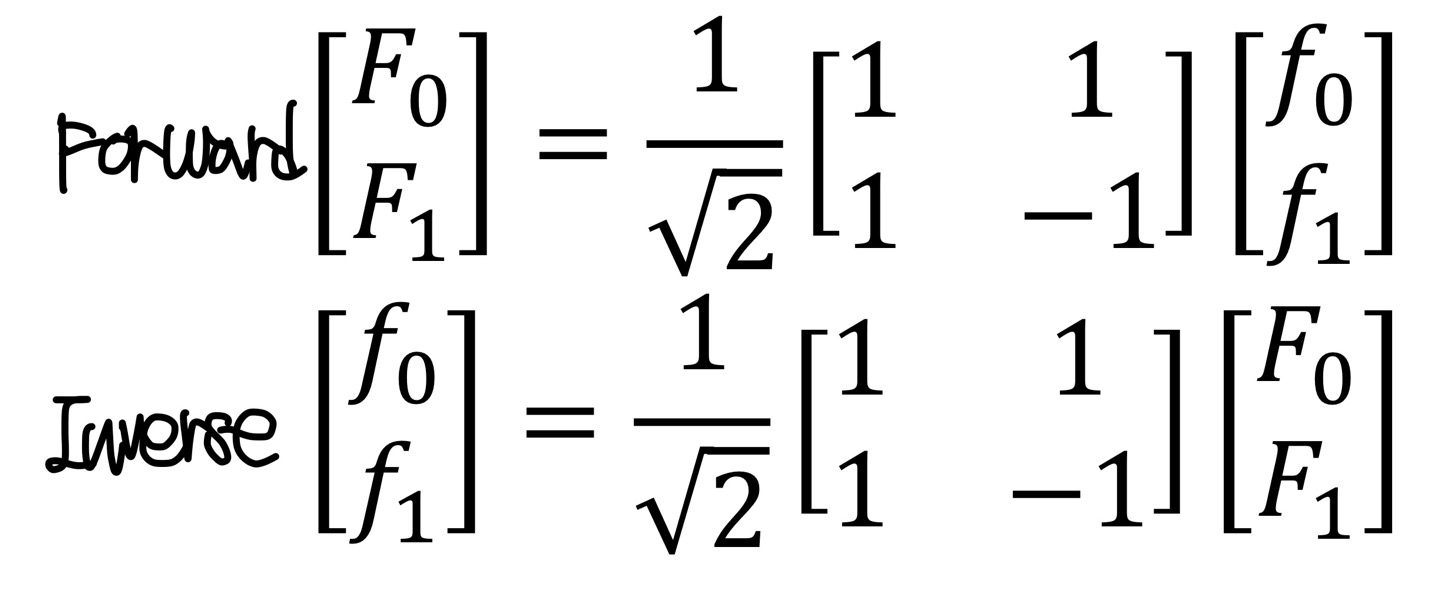
여기서 $1\over\sqrt 2$는 M의 값을 각각 evenly하게 분배해준 값이다.(앞에서 설명함)
w에 대한 matrix를 column space로 Linear combination하면 다음과 같다.

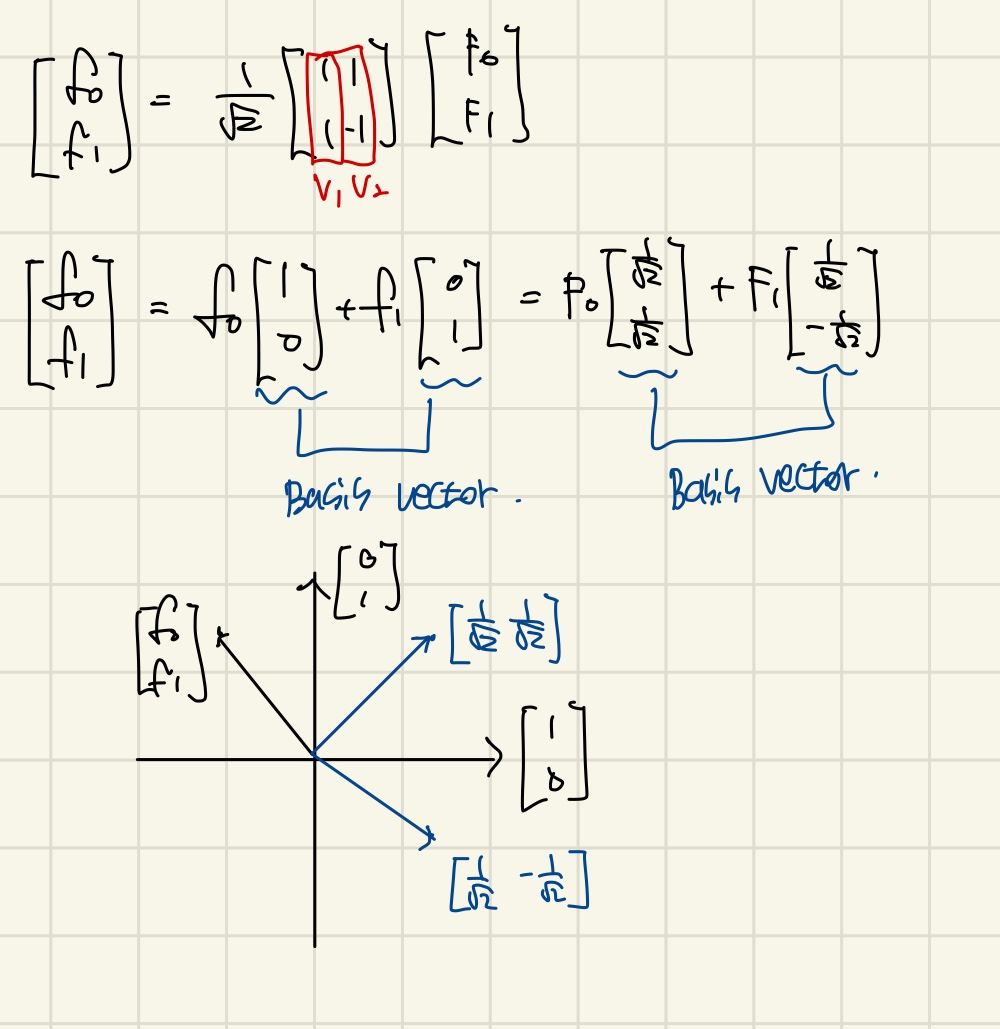
우리는 $f_o$와 $f_1$을 다른 basis vectors를 통해서 weighted sum으로 signal을 구할 수 있게 된다.
단지 $f_o$와 $f_1$인 frequency domain에서 $f_o$와 $f_1$를 표현할 수 있지만, time domain으로도 signal을 표현할 수 있다는 것을 보여준것 이다.

우리는 영상처리를 배우고 있으니 이러한 수식을 Image로 표현해보자.

위에서와 마찬가지로 M = 2의 값을 가진다는 것은 2개의 pixel값을 이용한다는 뜻이다.

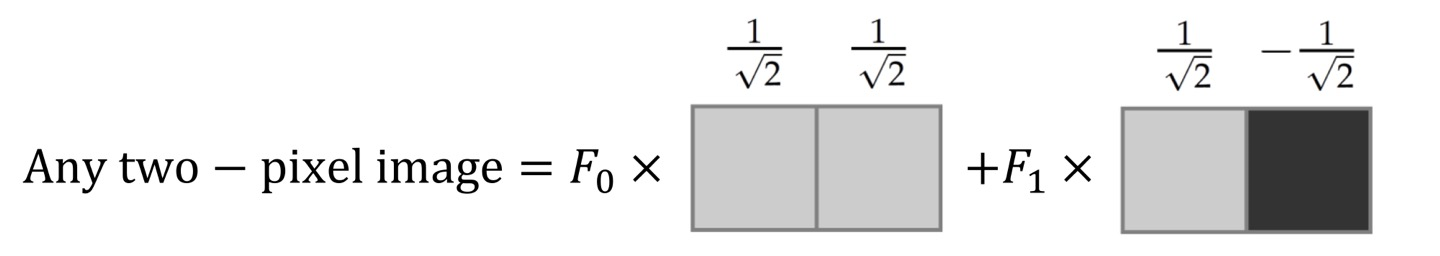
즉, Image를 time domain과 frequency domain으로 표현할 수 있는데 이때 1개의 Image를 여러 개의 frequency coefficient로 나누어서 low frequency Image와 high frequency image로 표현할 수 있게 된다.

이렇게 개념이 그렇다는 것만 알고 있으면 된다.

하지만 fourier coefficient와 basis의 image들은 대체로 Complex의 값이나 negative한 값을 가질 수 있다.(complex는 DFT의 exponential값을 오일러로 고치게 되면 나올 수 있습니다.)
그렇기 때문에 우리는 Magnitude와 phase로 image를 표현하게 됩니다.(frequency domain에서)

---

Complex image representation

우리는 complex value를 복소평면에다가 나타낸다.
다음은 복소평면을 나타내는 방법이다.

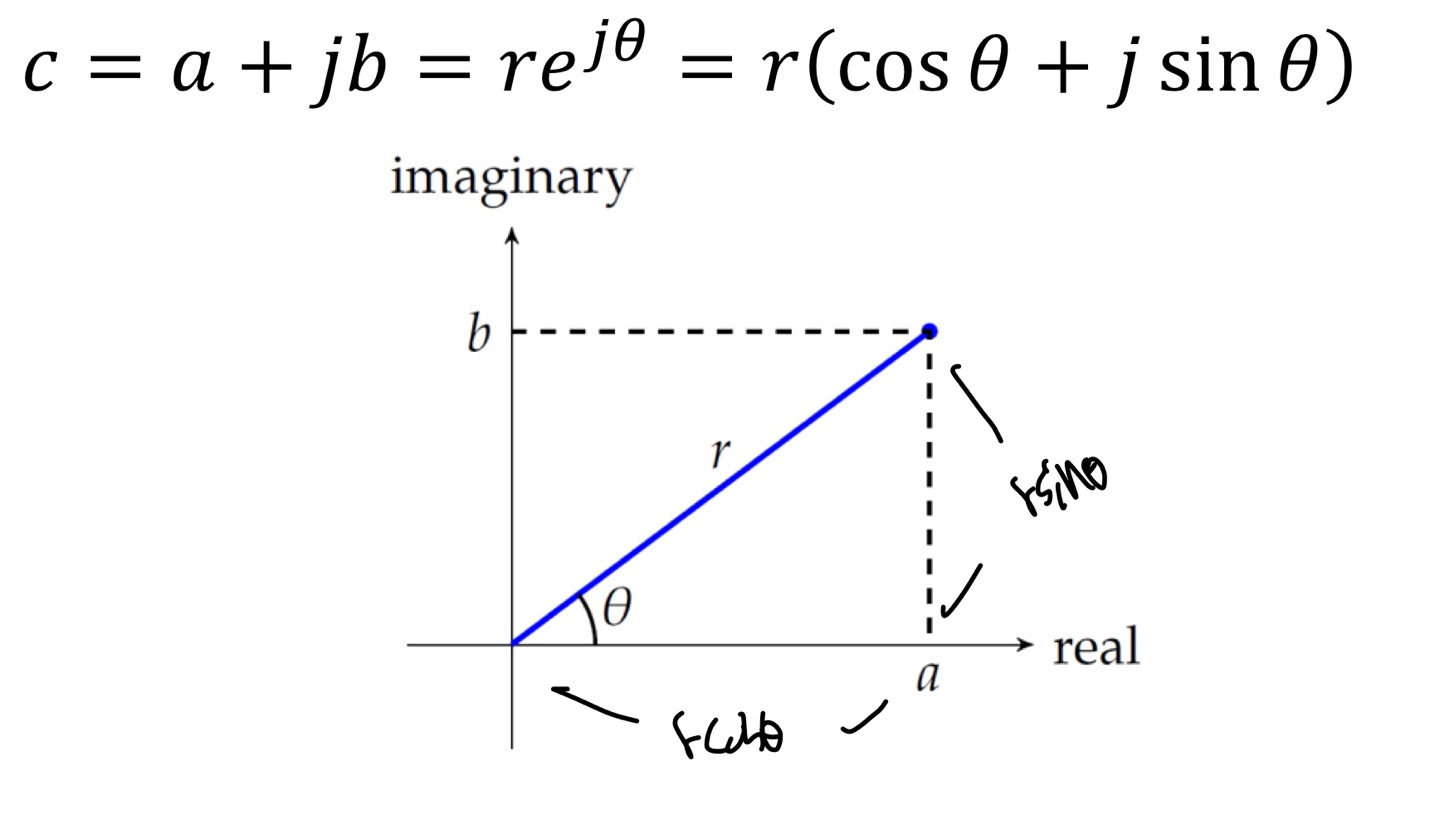
Complex Image는 magnitude(r)과 phase(Θ)의 Image로 대체적으로 보여준다.
또한 가끔씩 real값의 image와 imaginary값의 image를 보여주기도 한다.

다음은 frequency domain으로 변환하는 예시이고 M = 4이다.

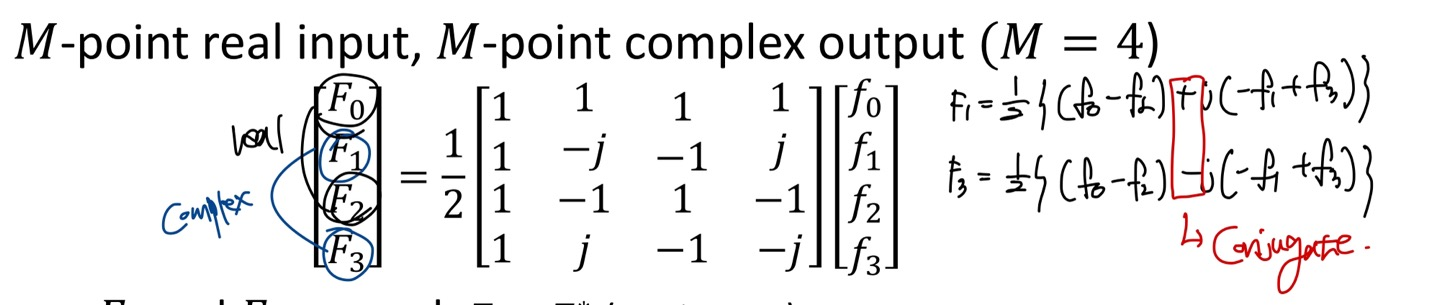
여기서 $F_0, F_2$은 real한 값을 갖고, $F_1, F_3$은 complex 값을 가진다.
중요한 특징은 $F_1, F_3$은 서로 imaginary의 부호만 다른 conjugate한 성질을 지닌다.
(frequency domain에서만 complex and negative의 값을 가지고 time domain에서는 그렇지 않다.)

정말로 그런지 M = 8일때를 생각해보자.

위의 예제는 8개의 f[x]의 값에서 F[u]로 forward 해주었다.
1/8값은 M = 8일때의 값을 나타낸 것이고 split하지 않은 모습이다.
u가 앞에서부터 0으로 차례대로 증가하는 값이라고 한다면, u = 0일때 9, u = 1일때, 3 + 0.6j ... 값을 가지게 된다. 이때 실수와 허수의 8개의 정보(M = 8)만 알게된다면 나머지 부분은 복소수에서 conjugate하면 된다.
이러한 성질을 "Hermitian"이라고 한다.

이때 에너지 보존의 관점에서 말하면, DFT는 transform이지만 에너지는 보존됩니다. dft는 에너지를 생성하거나 소멸시키지 않으며 transform 전의 image의 에너지와 transform 후의 frequency domain에서의 에너지는 동일해야한다.

이러한 DFT의 에너지 보존은 Parseval's theorm에 근거합니다.
이 정리에 따르면 time domain에서의 에너지와 frequency 에너지는 동일합니다.
수식을 나타내면 다음과 같습니다.

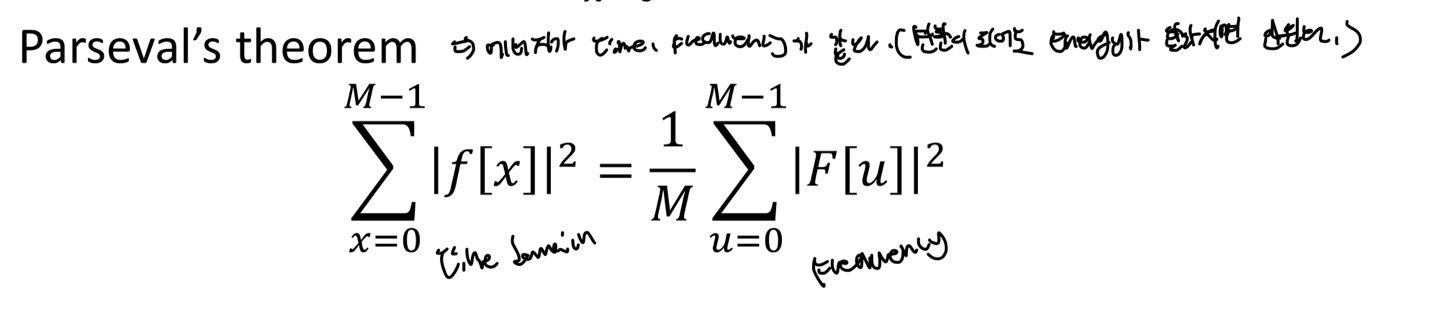
이러한 parseval theorm을 통해 DFT domain에서의 에너지를 구할 수 있으며 각 항은 time domain과 frequency domain에서의 에너지를 나타냅니다.

---

Fast Fourier Transform

하지만 실제로 우리가 DFT를 사용할때 M point에 대한 속도는 $O(M^2)$이기 때문에 매우 느립니다. 그렇기 때문에 우리는 FFT(Fast Fourier Transform)을 이용하게 되고 FFT는 $O(M logM)$으로 속도를 낮추었다고 합니다.

M에 대한 값이 커질수록 우리는 이러한 FFT는 더 나은 성능을 보여준다고 합니다.

FFT는 20세기에서 가장 좋은 알고리즘으로 TOP10안에 든다고 합니다.

출처는 J.Dongarra and F.Sullivan, "Introduction to the top 10 algorithms," Computing in Science Engineering, Jan.2000 입니다.

---

LTI System & Convolution

앞선 포스트에서 LTI System에 대해 설명했지만, 다시 한번 자세하게 설명한 후 더 심층적으로 다루겠습니다.

LTI System은 Linear time-invariant system으로 Linear와 time-invariant의 성질을 만족하는 system입니다.

다음은 Linear와 time-invariant에 대해서 설명합니다.

Linear

Linear system이 되기 위해서는 다음과 같은 두 개의 조건을 만족해야 합니다.

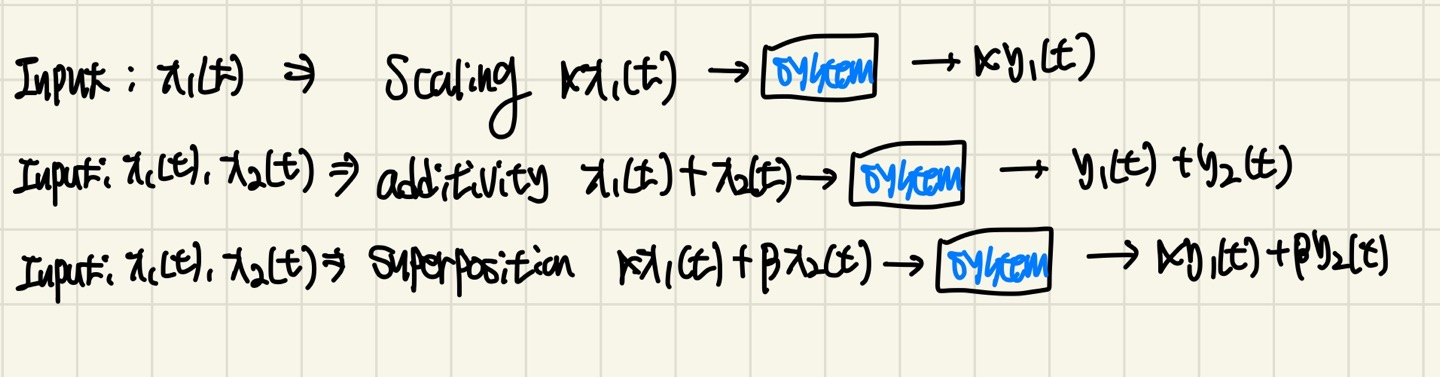
• Scaling : Input에 스칼라 값을 곱한다면 output에도 스칼라만큼 곱해져서 나와야한다.

• additivity : 두 개의 Input이 더해져서 들어오면 output은 더했던 두 Input의 output들 간 합해진 형태로 나오는 성질

만약, scaling과 additivity의 2가지 조건을 만족한다면 "Superposition"이라고 합니다.

Time-Invariant

• time-shift된 Input이 들어가면 동일하게 time shift된 output이 나오는 것을 의미한다.

다시 LTI system으로 넘어와서,
LTI는 Linear와 Time-Invariant성질을 만족하므로 임의의 Input 신호가 system을 거쳐 갈때 그 output값을 구할 수 있게 된다.
즉, 임의의 Input에 대해서도 예측이 가능하게 된다는 뜻이다.

LTI의 기본적인 수식은 y(t) = f(x(t), h(t))이다.
이때 x(t)는 Input이고, h(t)는 Impulse Response이다.
Impulse Response는 Impulse function(아주 basis한 함수)이 어떤 system에 들어왔을때 나오는 output이다.

즉, Impulse function을 system에 넣은 다음, 나온 반응을 보면 system을 알 수 있게 된다. 이렇게 나온 Impuse Response를 기반으로 주어진 우리가 원하는 Input x(t)가 들어갈대 output y(t)가 어떻게 나올지 알 수 있게 된다.

Impulse Function

Discrete Time Domain에서 Impulse Function

Continuous Time Domain에서 Impulse Function

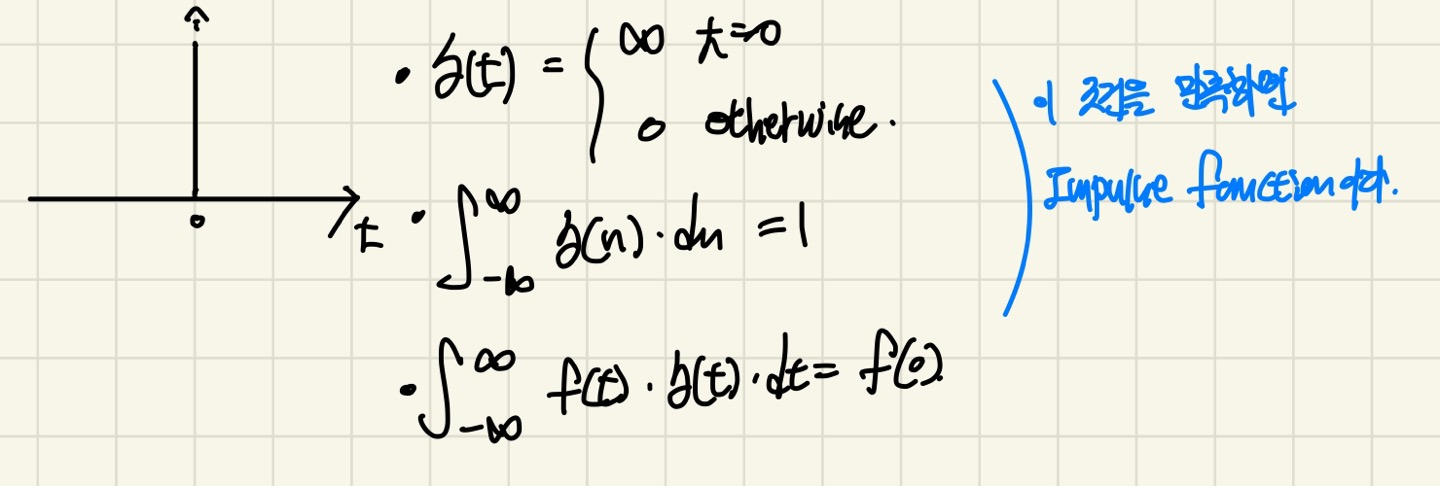
Discrete/Continuous Time Domain 그래프 옆의 3가지의 조건을 만족하면 Impulse Function 입니다.

Impulse Response

Impulse Response란 Impulse Function이 어떤 system에 들어갔다가 나오는 output이다.
Impulse Function δ(t)가 어떤 system에 들어갔다가 나온 output이 h(t)라는 이야기이다.

그렇다면 아까 LTI의 수식을 다시 보면 y(output) = f(x(t), h(t))에서 h(t)의 정의는 사전에 주어진 system에 Impulse Function을 한번 넣은 후 Impulse Response를 구한 다음 이 정보를 잘 조합해서 x(t)로부터 y(t)를 만들어보자는 것 입니다.

말이 어렵기 때문에 수식으로 보겠습니다.

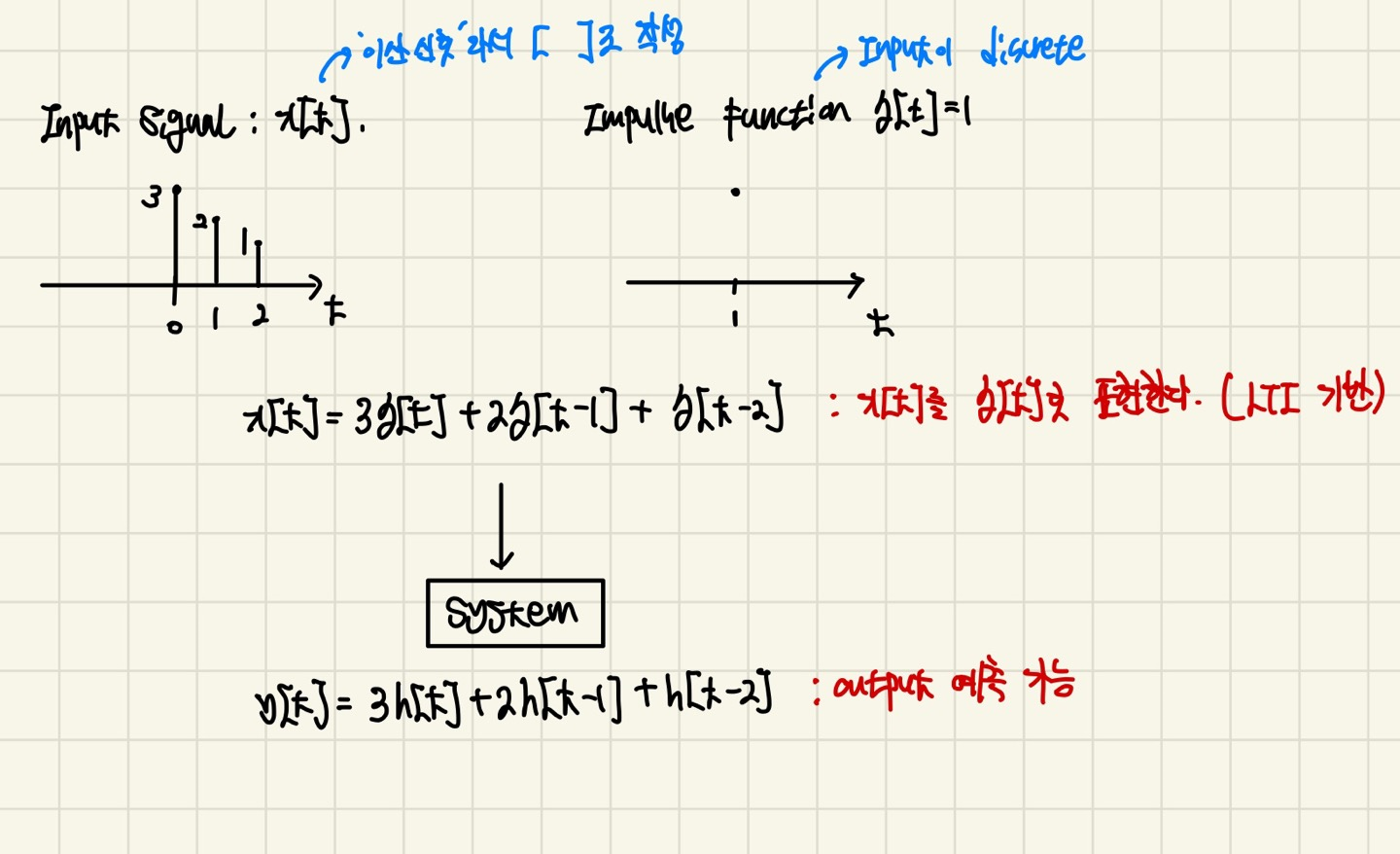
이렇게 우리가 Impulse Response와 Input x만 안다면 x를 Input으로 system에 넣었을때 output인 y를 쉽게 구할 수 있게 된다.

우리가 앞선 내용을 정리하면 Convolution을 알기 위함이였다.
Convolution은 Impulse Response의 조합으로 signal을 표현하기 위한것으로 LTI의 정수 그 자체이다.

예제를 살펴보겠습니다.

Input : f[n] = [4, 5, 0, 1, 2]
Impulse Response : h[n] = [1, 2, 1]

이라고 한다면, 전체 Convolution의 결과는 M + N - 1의 length를 갖습니다. 그러면 M = 5, N = 3이므로 5 + 3 - 1 = 7의 output length를 갖습니다.

Convolution연산을 해보면 다음과 같습니다.

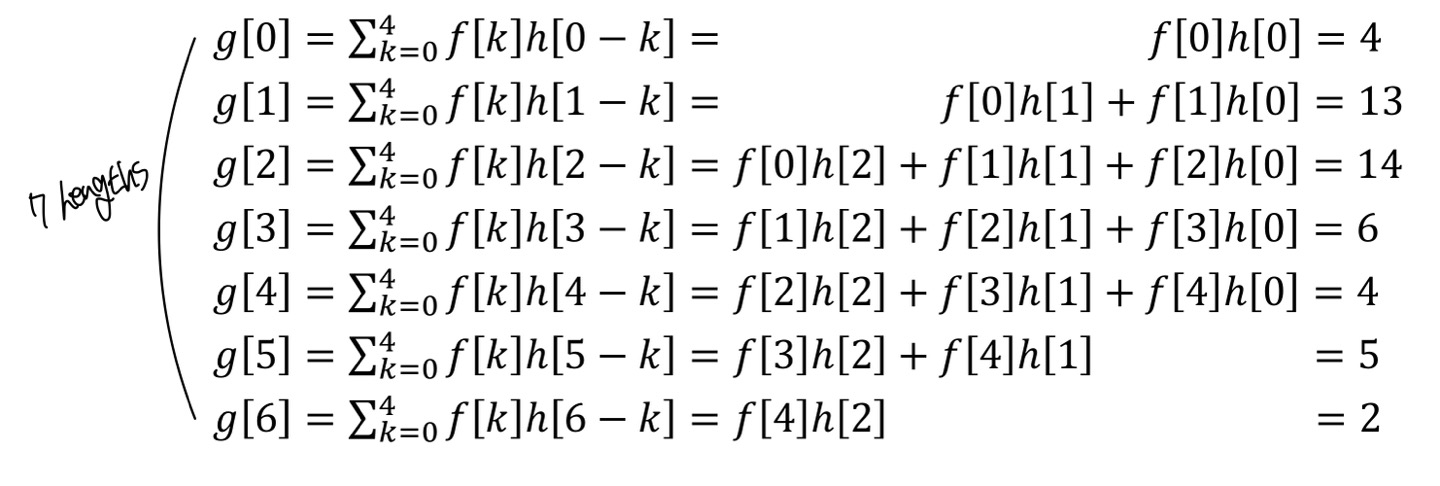
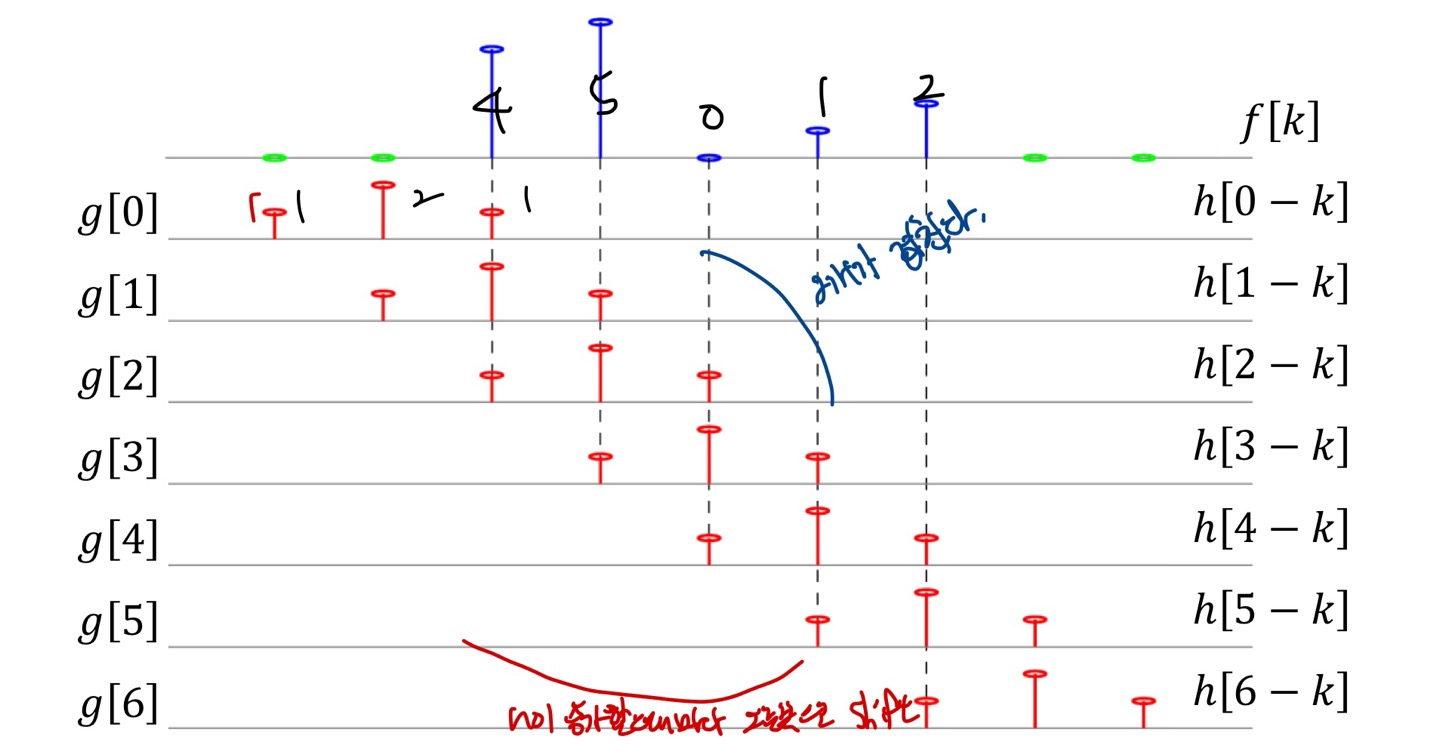
Convolution을 계산하면서 g[n]에서의 n값이 1씩 커질수록 Impulse Response값들이 오른쪽으로 shift되는 현상을 볼 수 있다. 이때 f[k]는 Input값이므로 constant이다.

---

Circular Convolution

앞선 Convolution은 Input Signal이나 Image의 가장자리 처리에 문제가 있을 수 있습니다. Image의 가장자리에 있는 Pixel들이 중요한 정보를 담고 있을때, Convolution을 사용하면 가장자리 부근에 정보 손실이 발생할 수 있습니다.

하지만 Circular Convolution은 Input을 circular 데이터로 간주하고, kernel을 Input에서 특정 위치로 이동시킬때 Input의 끝과 시작이 연결되어 있다고 가정합니다.(padding을 의미한다.)

수식을 나타내면 다음과 같다.

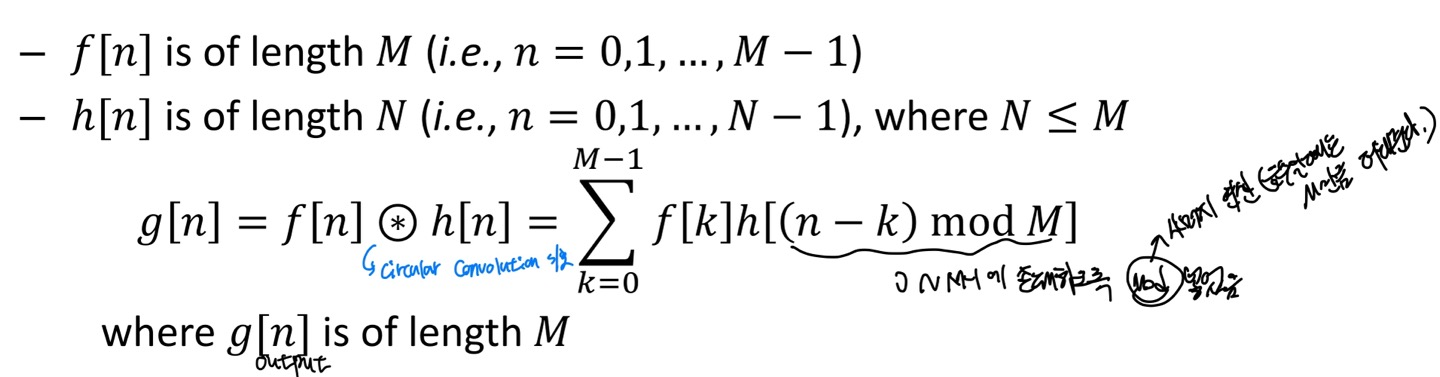
circular convolution의 기호를 보면 ⊛이다.
하지만 ambiguity가 없을때는 *을 circual convolution의 연산의 기호로 쓸 수 있다.

다음 예제를 보자

Impulse Response에 n-k가 negative한 값을 가지고 있다면 M값을 더해주면 된다. 만약 positive한 값(where <=M)라면 M으로 나눠준 나머지의 값을 구하면 된다.

또한 length가 앞에서 M이라고 한 이유는 output의 결과값이 M의 length를 지나고 나면 다시 반복되는 현상이 일어나게 된다.

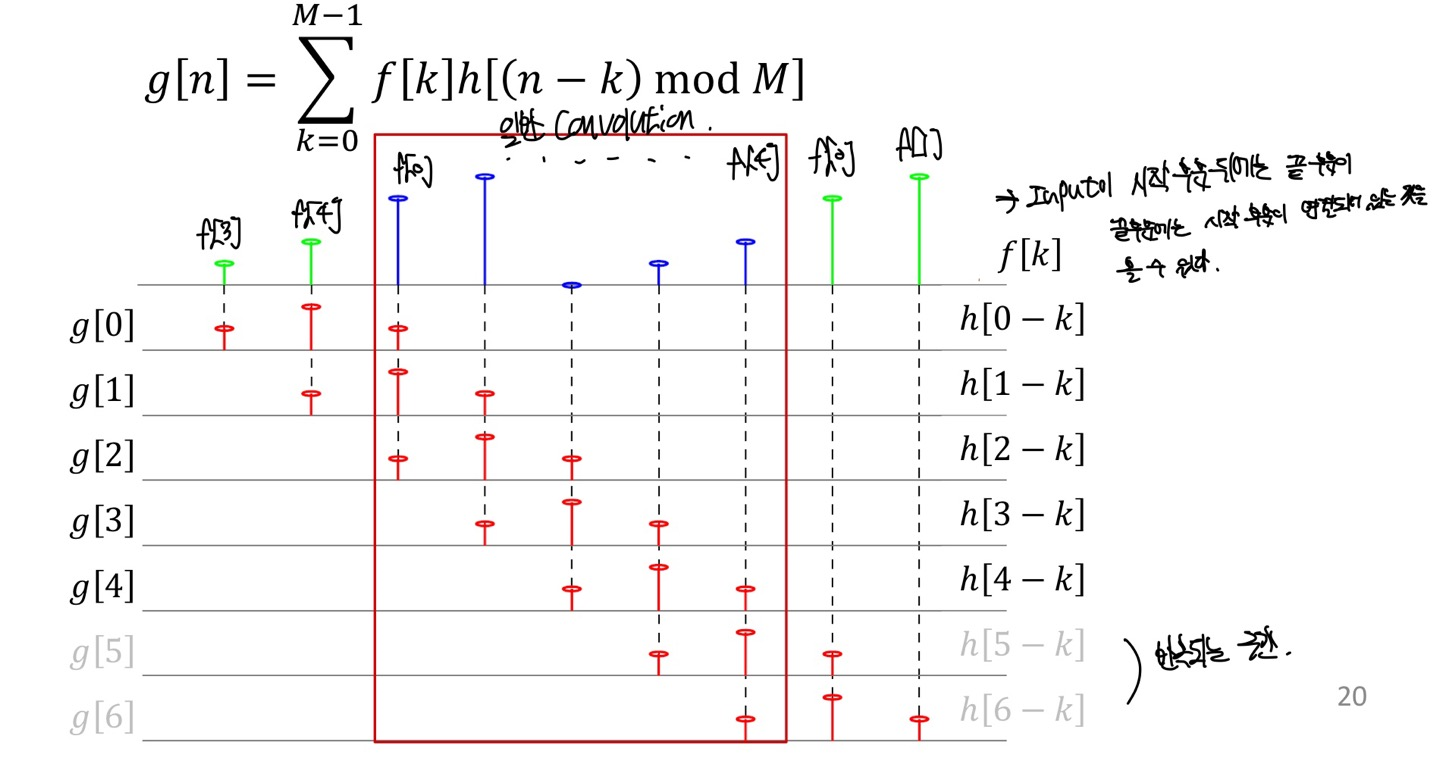
이 또한 그래프를 보게 되면 다음과 같다.
설명은 이미지안에 포함되어 있다.

FFT

Circular Convolution은 DFT를 사용하여 계산할 수 있습니다.
이때 FFT의 전제조건은 f[n]과 h[n]의 길이가 같아야합니다. 이것은 circular convolution의 정의와 같습니다. 처음과 끝, 끝과 처음이 이어져있는 것이 아닌, 일반적으로 zero-padding을 h[n]에 해준다고 생각하시면 됩니다.(f를 image, h를 kernel이라고 생각하면 됩니다.)

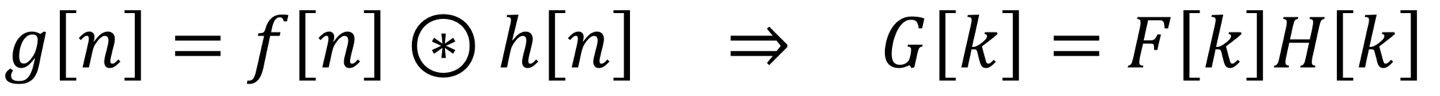
F[k]는 DFT{f[n]}이고, H[k]는 DFT{h[n]}입니다.
각 sequence별로 DFT를 사용하여 Time Domain에서 Frequency Domain에서 곱셈을 수행합니다.
이때 나온 output값을 Inverse DFT를 사용해주면 Time Domain으로 변환 됩니다.

이러한 방식으로 DFT를 사용하면 Circular Convolution을 효율적으로 계산이 가능합니다.

그러나 일반적인 Linear Convolution이 더 realistic하며 Linear Convolution을 대신 쓸때가 있는데 이때는 computation을 줄일 수 있고, h[n]의 effect를 이해하기 위해서 사용합니다.

만약, boundary에 zero-padding을 적용했다고 하면 우리는 Linear Convolution을 시행하기 위해 Circular Convolution을 이용할 수 있습니다.(circular를 대신 이용한다.)
반복되는 range만 가져오면 되기 때문이다.(앞선 그림에서 repeat되는 현상을 볼 수 있었기 때문이다.)