우리는 이때까지 digital images들을 handling하는데에 기초를 쌓았다.
하지만, digital images는 ideal하지 않기 때문에 3가지의 objectives를 지닌다.

• Image Enhancement

• Image Restoration

• Image Reconstruction

이 포스트에서는 Image Enhancement를 중점으로 설명합니다.

---

Metric

MSE

우리가 MxN의 size인 f의 Image가 있고 똑같은 size의 $f^h$이 있다고 하자.
이때 f는 ideal한 Image 즉, 깨끗한 Image를 뜻하고, $f^h$은 Image Restored된 것이라고 하자.

만약 $f^h$가 Restoration이 잘 되었다는 평가 지표가 필요하다. 이 평가지표는 MSE(Mean Squared Error)를 쓰게 된다.

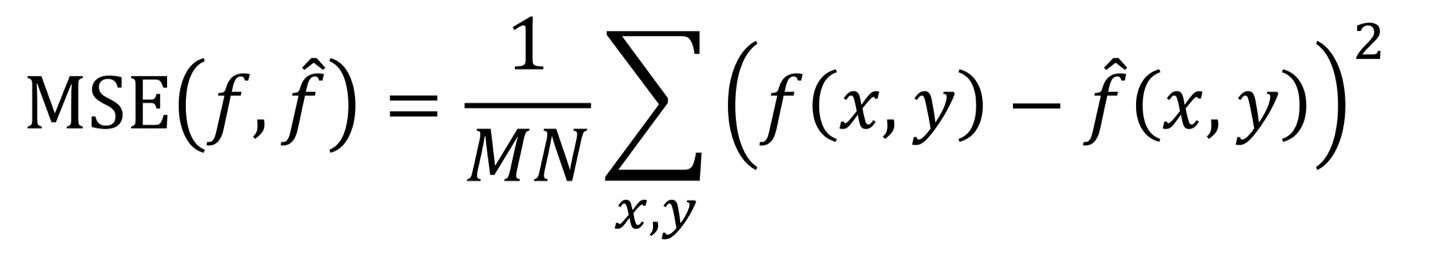
ideal image - restored image의 square한 값인데, 이것은 각 x,y에 각각 대응되는 pixel값들을 빼주게 된다. 이것을 $\frac{1}{MN}$으로 Normalized하여 Restoration의 성능을 알아보게 된다.(Σ가 2개가 있어야 맞지만, 임의대로 표시한 것입니다.)

만약 MSE값이 0 이라면, restored image가 ideal image가 되었다라는 것이다.(필요충분)
하지만, MSE값이 large value를 가지고 있다면, $f^h$은 f와는 매우 다른 image를 가지고 있다는 것이 된다.

MAE

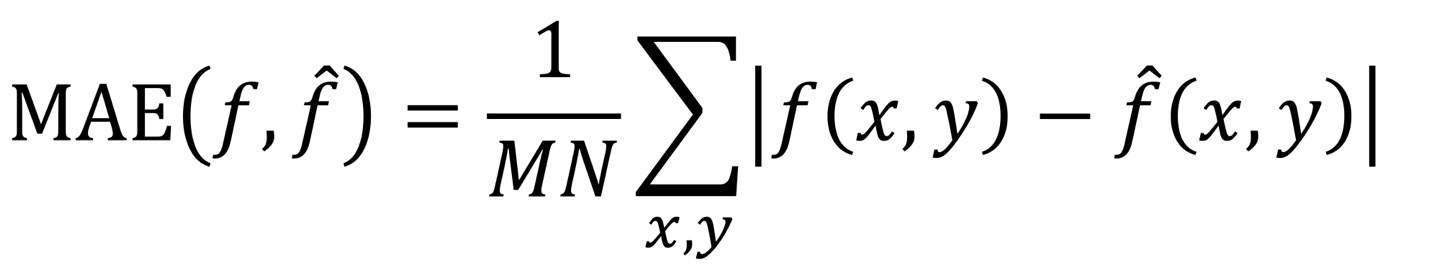
MAE는 절댓값을 취하는 평가 지표로 MSE와 달리 이상치에 덜 민감하다는 특징이 있다.
즉, 값의 크기에 관계없이 모든 오류에 동일한 가중치를 부여하고 각 오류를 동일한 중요성으로 처리한다는 특징이 있다.

이러한 특징으로 Image의 Edge를 보존할때 유용하다. 왜냐하면 Edge는 변화량이 높기 때문이다.(sharp하다.) 또한, image/video 압축에 많이 사용된다고 한다.

SNR(Signal-to-Noise-Ratio)

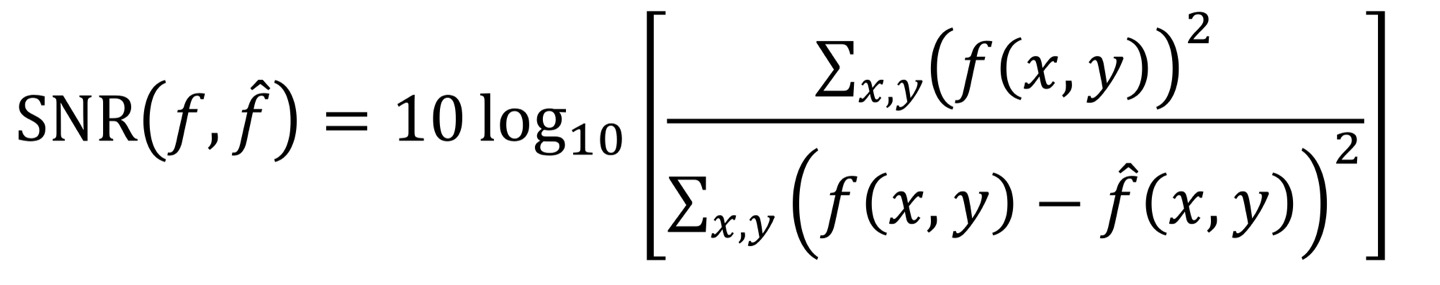
분자는 ideal한 image의 energy이다. 즉, 모든 pixel의 squared 값이다.
분모는 MSE의 Normalized한 부분($\frac{1}{MN}$)만 빼면 같은 식이다. Noise의 energy라고 생각하면 된다.

이 값의 unit(단위)는 dB(decibel)이며, 30dB이상이면 좋고, 20db보다 낮으면 좋지 않은 성능을 가진다고 판단하면 된다.

PSNR(Peak-Signal-to-noise Ratio)

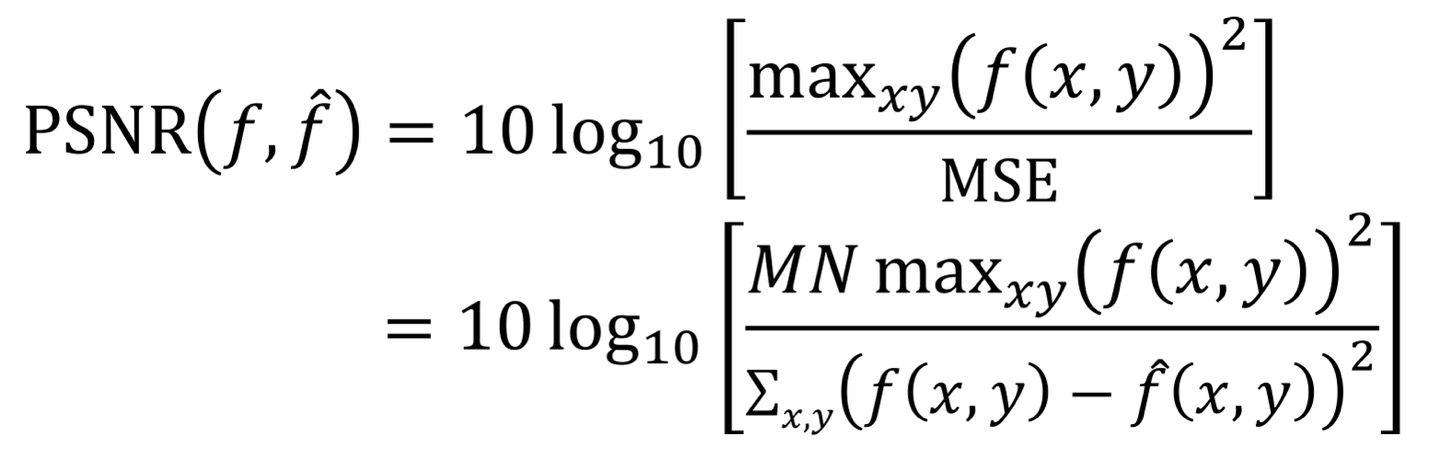
분자는 ideal한 image의 특정 위치에서의 pixel값이 가장 높은 값을 말한다.
분자는 말 그대로 MSE를 나타내고 MSE의 식을 풀어내면 아래의 식을 정리한 것과 같다.

PSNR은 영상처리에서 metric으로 가장 많이 사용되는 것 중 1개이다.

---

Noise Removal

Noise는 우리가 어떤 Image를 찍을때 원치 않은 정보를 말한다. 예를 들어, 달의 사진을 찍고 싶은데 달의 밝기로 인해 달의 표면이 보이지 않는다면 그것도 Noise가 될 수 있다.
즉, 외부의 방해로 인한 Image의 degradation의 한 종류이다.

이러한 Noise를 제거하기 위해서는 우리는 Noise의 Model을 먼저 추정하여 Noise에 종속적으로 Image를 Restoration하는 방법으로 접근하는 것이 가장 simple하다.

Noise의 type들은 다음과 같습니다.

• Salt and pepper noise: 카메라에 dead pixel이 있으면 발생합니다.

• Gaussian noise : 대부분의 경우의 noise를 차지합니다.

• Speckle noise : 주로 의료 영상에서 발생하는 noise입니다.

• Periodic noise : 주파수 변화에 따른 noise입니다.

더 많은 Noise들이 있겠지만, Gaussian Noise를 제거해보는 기법을 배우겠습니다.

한가지 말할게 있다면, 우리는 Image를 얻을때 이전 포스트에서 말했다싶이, 우리가 촬영한 Image + Noise가 섞여서 Image가 나온다고 했습니다.

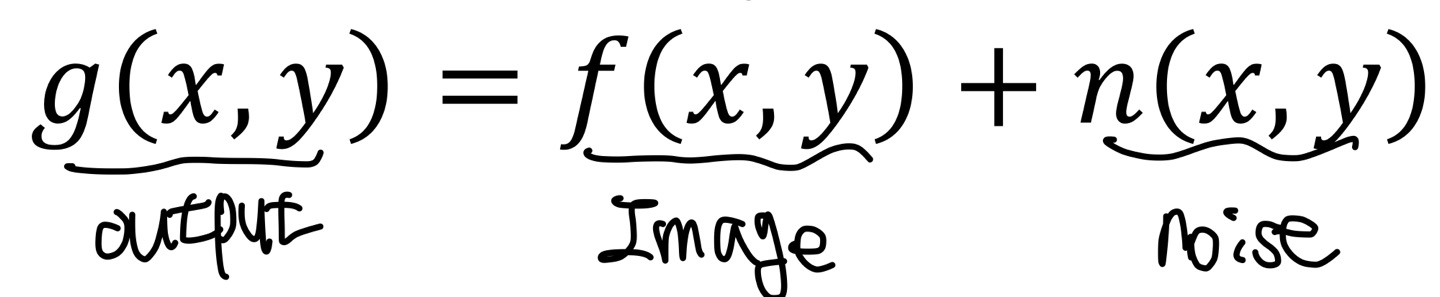
Median filter

(여기에서의 noise는 salt-and-pepper noise를 말합니다.)
단순히 noise를 제거하기 위해서 Low-pass filtering을 사용할 수 있습니다. 하지만, 일부 noise를 제거할 수는 있지만, 완벽하게 제거한다는 기대는 어렵기도 하고 Edge의 정보를 손실하다는 것이 가장 치명적입니다.

Median filter는 noise를 제거하는데 매우 효과적이며 edge를 잘 보존합니다.
edge를 잘 보존한다는 것은 Image의 object에 대한 structure를 잘 보존한다는 것입니다.
새로운 pixel값을 만들지 않기 때문에 filtering과정에서 추가적인 정보 손실이 나지 않고 Image의 특성 부분이나 데이터의 중요한 특성을 보존할 수 있습니다. 또한, Impulse pixel값에 매우 효과적입니다.

Median filter의 procedure는 다음과 같습니다.

• kernel안에서의 pixel값을 오름차순으로 sorting합니다.

• output 값으로 median value를 선택합니다.

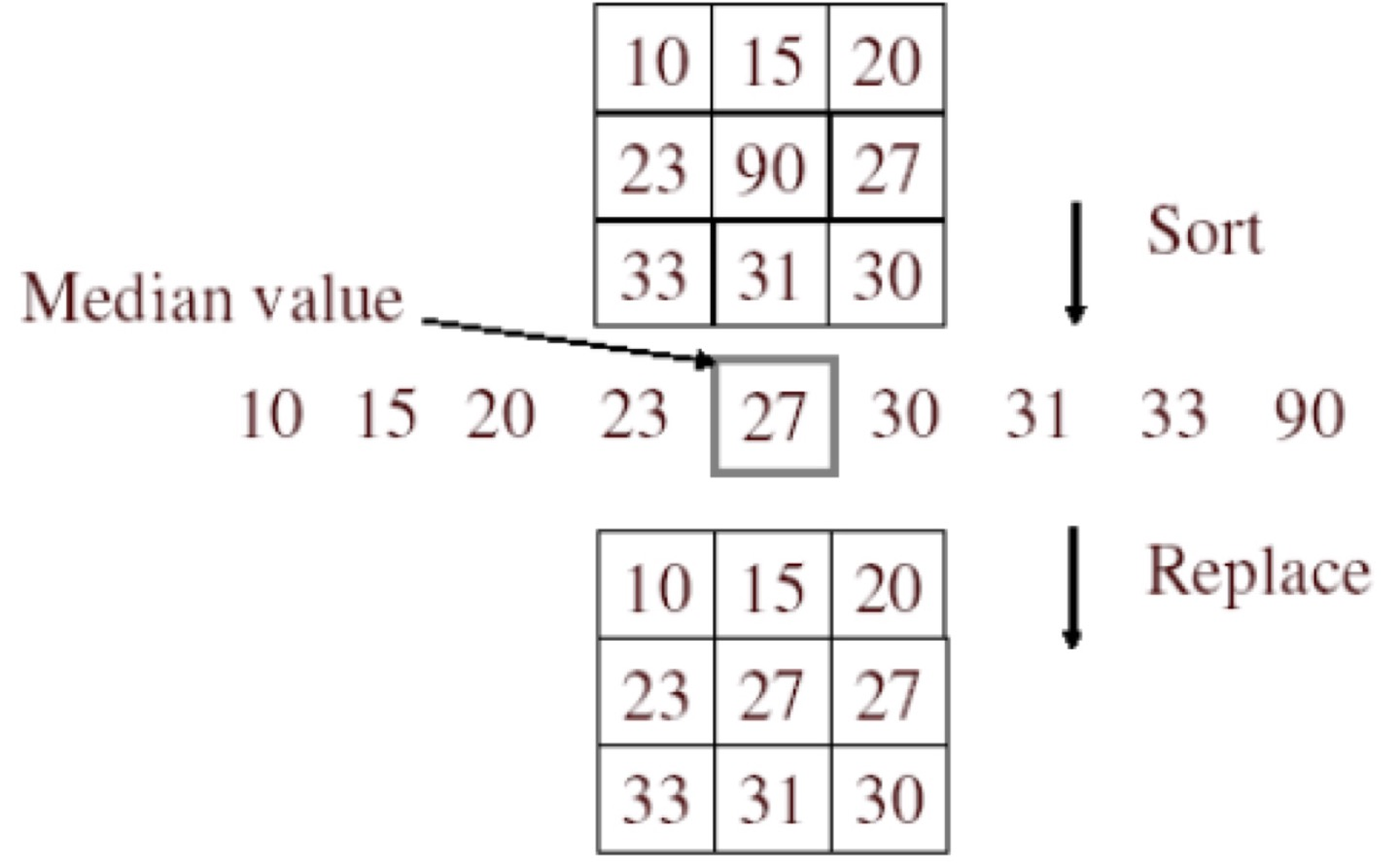
하지만 Median filter의 procedure에서 오름차순으로 sorting하는 과정이 $O(n^2)$의 연산량이 필요하기 때문에 매우 느립니다.

그래서 나온 idea는 noise(Salt-and-Pepper noise)는 neighboring pixel값들에 대해서 매우 이상치의 값을 가지고 있다는 것이 핵심이라고 봤다.

Procedure은 다음과 같다.

• thershold값 D를 선택합니다.

• kernel안의 center pixel(p)을 제외한 neighboring pixel들의 평균 값과 center pixel을 비교합니다.

• 만약 |p-m| > D라면, p는 noise이고 그렇지 않으면 noise가 아니라고 판정합니다.

• 만약 noise라고 판단이 되면 m을 p로 초기화 시켜줍니다.

Wiener filter, Bilateral filter, NLM

(여기서부터 말하는 noise는 Gaussian noise입니다.)

Gaussian Noise

Gaussian noise는 Gaussian 분포를 따르는 확률적인 noise로, 특정한 패턴이나 규칙 없이 image의 각 pixel에 더해지는 noise입니다.
noise를 처리하려는 대부분의 접근법은 Gaussian noise로 추정한다고 보면 됩니다. 왜냐하면 그만큼 이 noise가 많이 발생하기 때문입니다.

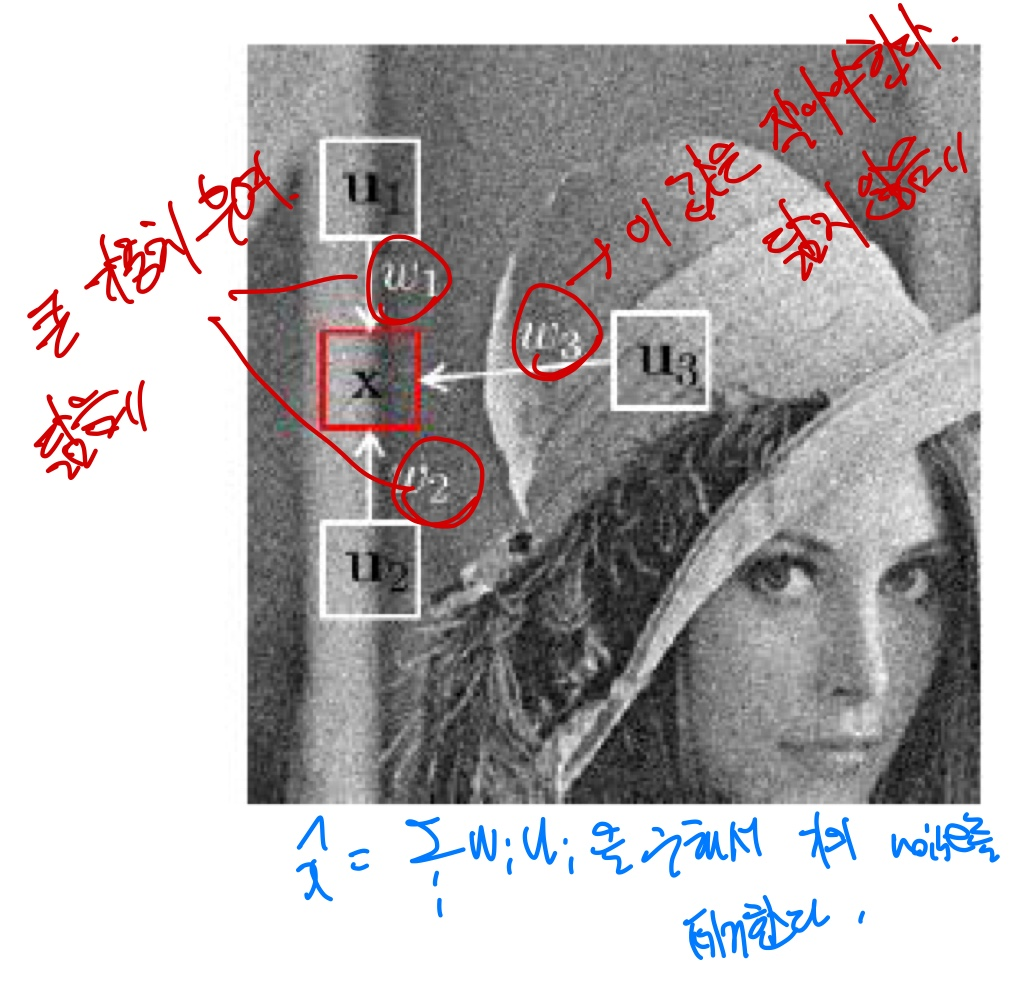
그렇다면 왜 noise가 있는 여러 개의 image를 average하게 되면 noise가 감소하는 것일까?

100개의 noisy image들이 있다고 하자.
100개의 image를 촬영할때마다 우리는 noise의 형태가 바뀌게 된다(random한 형태의 noise). 그렇다면 아무리 똑같은 것의 image를 찍게 되어도 100개의 noise의 분포도가 다른 서로 다른 image라는 것이다.

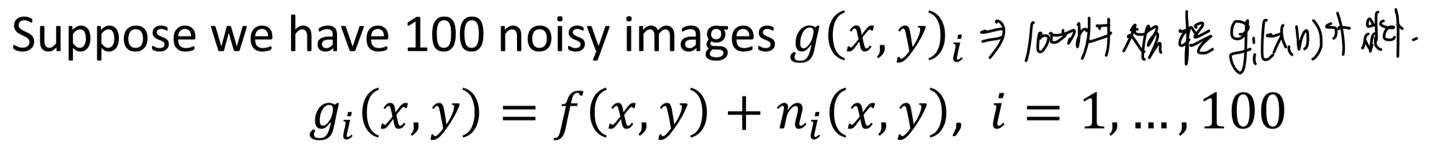
하지만, 실제로 우리는 1개의 image만을 가지고 있을 것이다. 그래서 앞서 Salt-and-pepper noise에서 Low-pass filter를 적용해도 된다. 하지만 kernel size가 작다면 noise가 잘 제거되지 않을 것이고, 크다면 noise를 제거하는데는 효과적이지만 과도하게 blur처리가 된다는 단점이 있다.

우리는 대안으로 kernel안의 pixel값들의 따라서 characteristics를 adaptively하게 바꾸는 방법을 제안했다.

이 방법들에 대해서 소개하겠다.

Wiener filter

Wiener filter는 kernel을 image에다가 씌우고 평균과 분산값들을 통해 Edge가 유지되는 Image를 만들도록 한다.

• m(x,y) : kernel element들의 평균 값

• $σ^2_g$ : kernel element들의 분산 값

• $σ^2_n$ : Image의 noise 분산 값

• g(x,y) : kernel의 center pixel 값

m(x,y)는 kernel element의 평균 값이므로 이미 Low-pass filter를 적용시킨 값이 되므로 noise가 섞여 있지 않게 된다. g(x,y) - m(x,y)는 원래의 pixel값에서 Low Frequency의 값만 빼주었으니 High frequency의 값만 가지게 되는데, 이때 noise와 edge를 포함하게 된다. 그것을 일정한 비율로 나누어주고 Low frequency와 더해주니 noise를 제거하면서 edge를 보존할 수 있게된다.

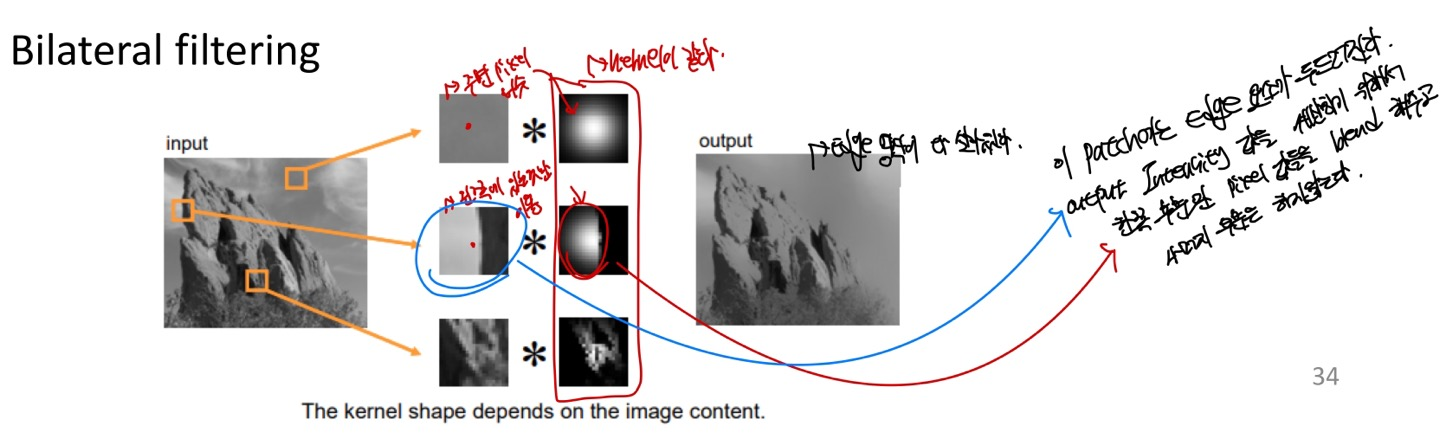
Bilateral filter

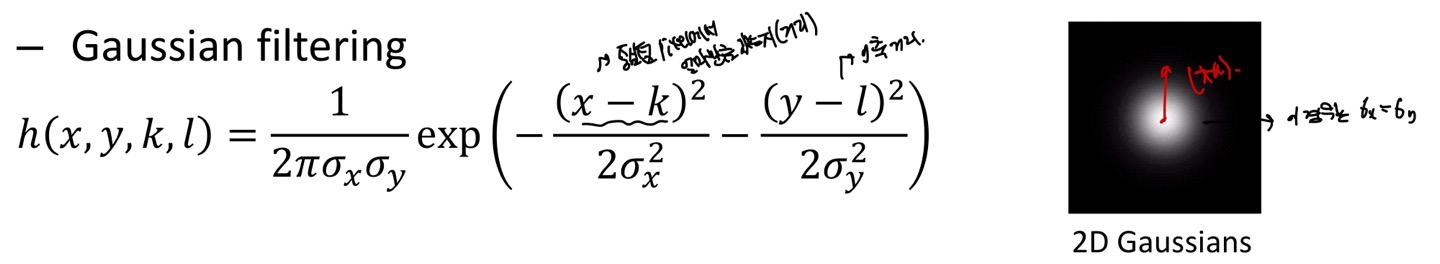
Bilateral filter를 보기전에 Gaussian filter를 보겠습니다.
Gaussian filter의 문제점은 모든 pixel에 같은 Gaussian kernel을 사용하기 때문에 edge가 심하게 존재하는 patch에 대해서 Gaussian kerenl을 곱하게 되면 극명하게 들어나는 intensity(Edge)에 대한 값도 포함되어 blur 처리가 됩니다.

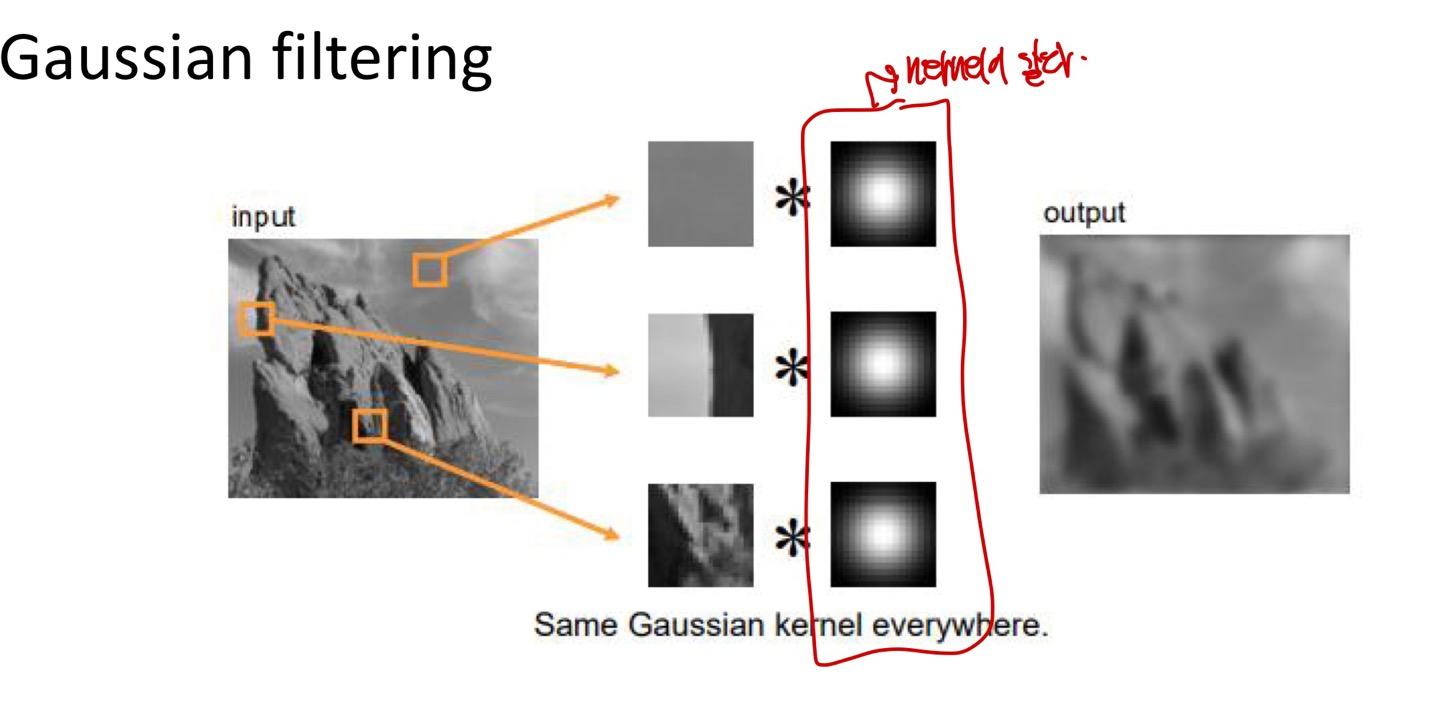
Gaussian filter에 대한 대안으로 우리는 Bilateral Filter를 배우게 됩니다.

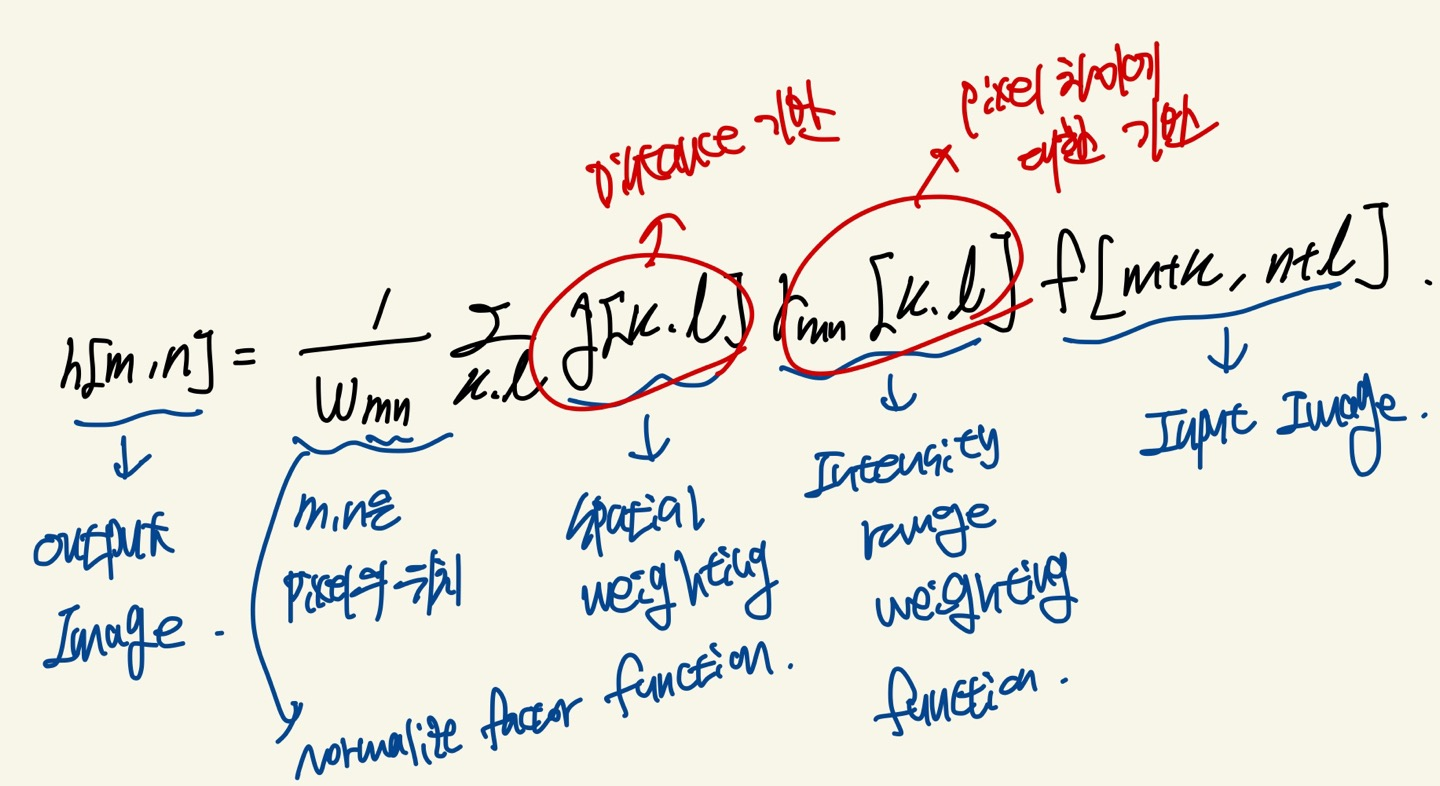
먼저 수식을 보면 다음과 같습니다.

하늘색으로 쓴 Distance는 Spatial weighting이고, Pixel이라고 쓰여져 있는 것은 Intensity Range weighting이고 $\frac{1}{N}$은 output image를 normalize하는 역할을 하는데 energy를 보존하기 위해 사용합니다.(합을 1로 맞추기 위해)

Spatial weighting은 Gaussian filter와 마찬가지로 Sptial weighting function이 모든 pixel과 곱해집니다.(target pixel에 가까울수록 큰 값을 곱해줍니다.)

Intensity weighting은 target pixel과 비슷한 Intensity값을 가지는 pixel에 더 큰 weight를 부가합니다.

조금 더 단순한 수식을 보여드리겠습니다.

Hyperparameter는 $σ_s$와 $σ_r$이 있습니다.

$σ_s$는 Spatial weighting function의 크기를 조절하고 값을 키우게 되면 sptial weight의 범위를 넓히게 되어 작은 detail을 효과적으로 제거할 수 있습니다.

$σ_r$은 Intensity range weighting function의 크기를 조절하고 값을 키우게 되면 Intensity 값의 차이가 큰 edge를 제거할 수 있습니다.

NLM(Nonlocal means filtering)

우리는 앞에서 여러 개의 image들을 average해준다면 noise가 없어진다는 idea를 읽었을 것 입니다.
이 idea로 우리는 image내에서 비슷한 image(Self-similarity)만을 crop하여서 image를 average하는 방법을 말합니다.

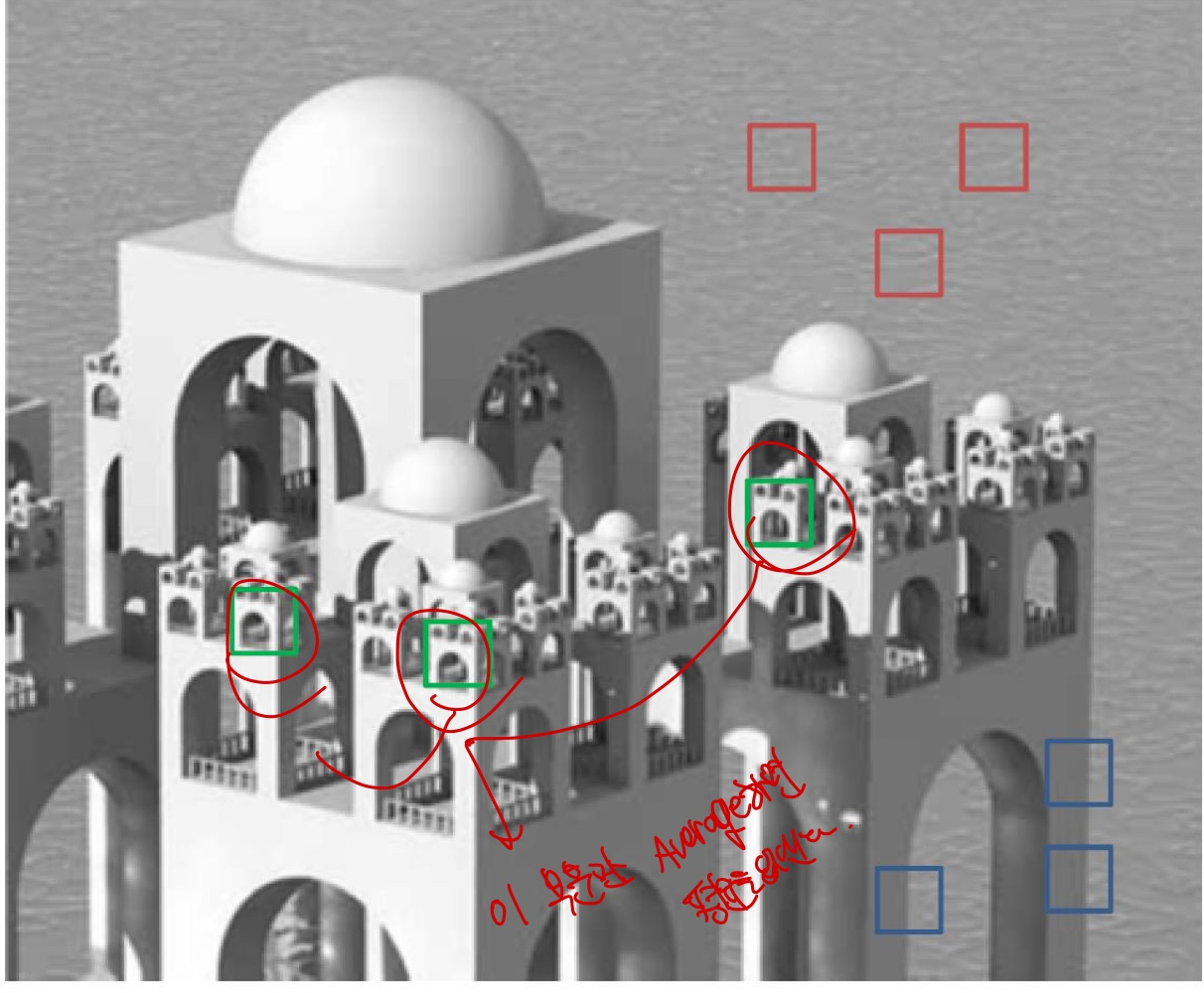
하지만 이러한 patch들은 실제로는 다르기 때문에 단순히 평균화를 시키는 것은 잘 작동이 되지를 않기 때문에 다음과 같은 알고리즘을 적용시킵니다.

• Replaces a block with a weighted average of all blocks

• More similar blocks are assigned bigger weights