그래프가 무엇인지 개념과 작성 법을 이전 포스팅 에서 소개하였다.
그래프에는 다양한 알고리즘이 존재한다.
최소 비용 신장트리: Prim 알고리즘, Kruskal 알고리즘
그래프 탐색 알고리즘: 깊이우선탐색(DFS), 너비우선탐색(BFS)
최단 경로 알고리즘: Dijkstra 알고리즘, Floyd-Warshall 알고리즘
그래프를 활용한 다양한 알고리즘이 이외에도 많이 존재한다.
그 중에서 코딩 테스트에서 매우 자주 나오고 중요한 DFS, BFS 가 무엇인지 알아보고 실제 문제는 어떻게 나오는지 알아보고자 한다.
그래프 탐색 알고리즘
그래프 탐색 알고리즘은 하나의 정점에서 순서대로 모든 정점을 한 번씩 방문하는 알고리즘을 말한다.
내가 생각했을 때 그래프 탐색 알고리즘은 2차원 배열에서 탐색 문제를 만나면 그래프 형태로 바꾸어 풀이하면 유용할 것이라고 생각한다.
해당 알고리즘에는 대표적으로 DFS, BFS 가 있다. 두 알고리즘의 차이점에 대해 알아보자.
깊이 우선 탐색(DFS: Depth First Search)
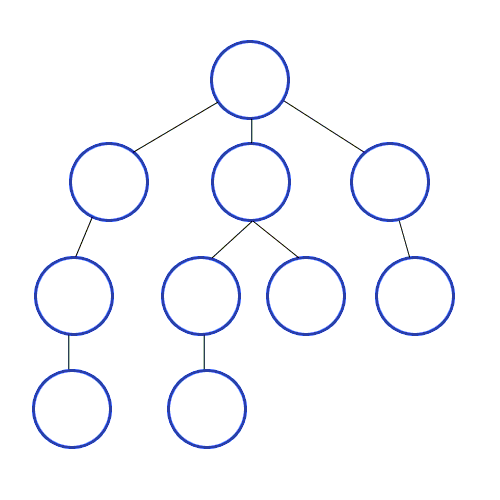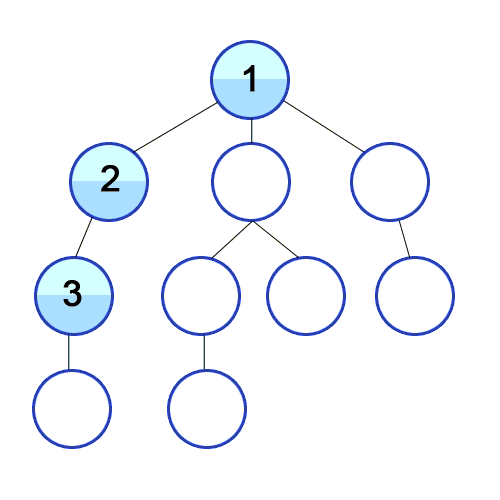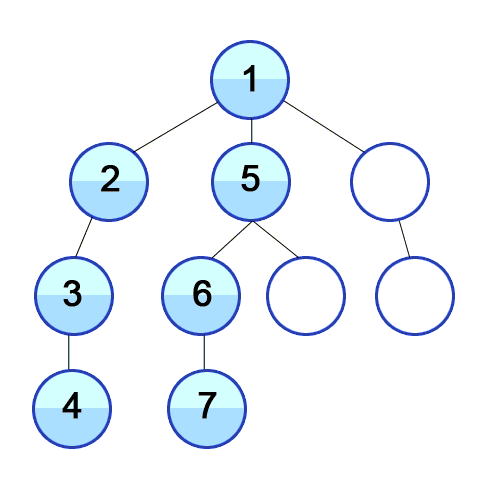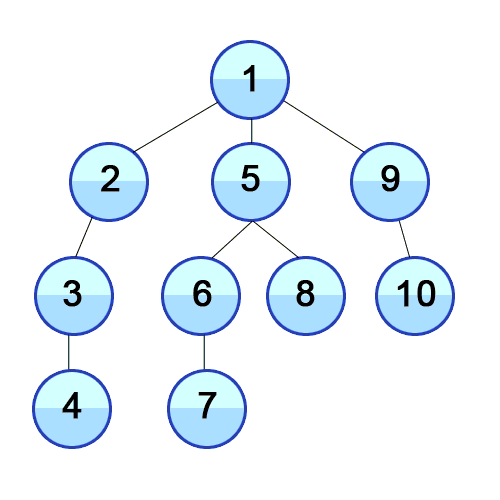
위 그림을 통해 보면 트리로 구성 되어있는 것을 볼 수 있다. "그래프에 대해 보여준다고 하지 않으셨나요?" 라고 할 수 도 있다.
하지만 트리도 그래프이다. 1번부터 10번까지 방문하는 순서를 보여준다.
정의
깊이 우선 탐색은 한 정점에서 방문하고 해당 정점과 인접한 정점을 계속해서 방문하는 방식이다. 인접한 정점이 없으면 다시 처음 방문했던 곳으로 돌아와 방문하지 않는 정점을 방문한다. 이때 다시 방문했던 곳으로 돌아오기 위해 재귀함수를 사용한다.
구현
인접 행렬을 이용한 구현과 인접 배열을 이용한 구현 둘 다 가능하다. 다만 인접행렬의 경우 인접 정점을 탐색하기 위해 모든 정점과 연결된 모든 정점을 확인해야 하기 때문에 O(n²) 의 복잡도를 가진다.
인접 리스트의 경우 정점 방문 개수 n 과 이와 연결된 간선의 개수 e 를 더한 O(n+e)의 복잡도를 가진다.
방문했는지를 visited 배열에 저장한다.
인접 행렬
int visited[MAX_VERTICES]; // 방문 노드 저장
// 인접 행렬 dfs
void dfs_mat(GraphType *g, int v) {
int w;
visited[v] = TRUE; // 정점 v 방문
printf("%d ", v);
for(w=0; w < g->n; w++) // 인접 정점 탐색
if(g->adj_mat[v][w] && !visited[w])
dfs_mat(g, w); // 정점 w 로 새로 방문
}인접 리스트
int visited[MAX_VERTICES]; // 방문 노드 저장
// 인접 리스트 dfs
void dfs_list(GraphType *g, int v) {
GraphNode *w;
visited[v] = TRUE; // 정점 v 방문
printf("%d", v);
for(w=g->adj_list[v]; w; w=w->link) // 인접 정점이 나오지 않을 때까지 탐색
if(!visited[w->vertex])
dfs_list(g, w->vertex) // 정점 w 로 새로 방문
}너비 우선 탐색(BFS: Breadth First Search)
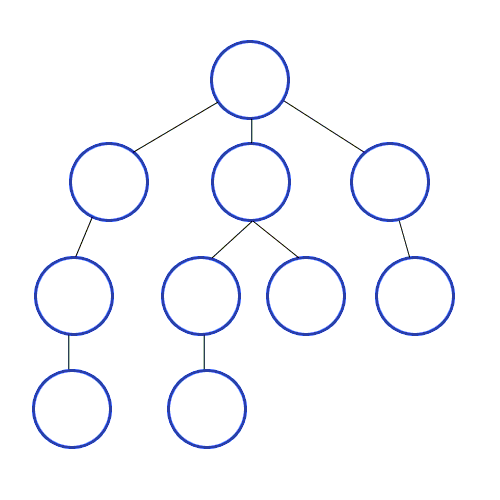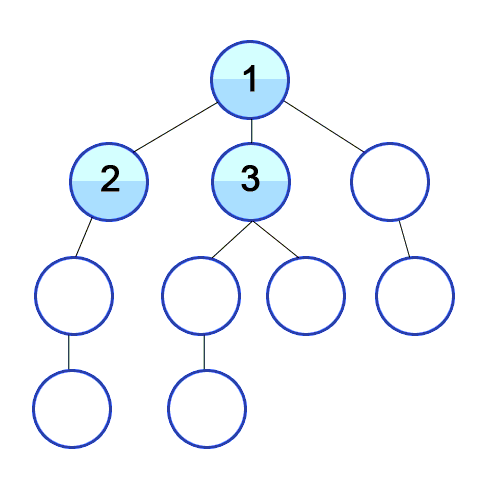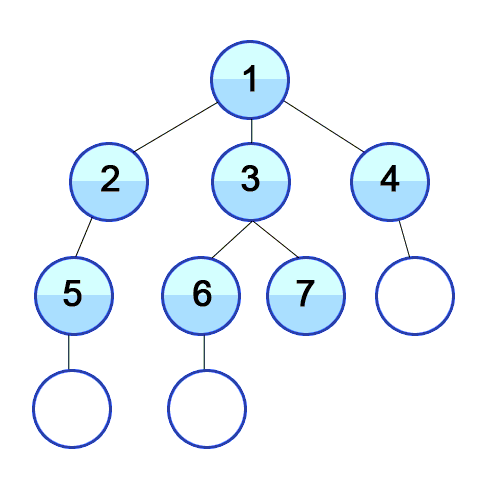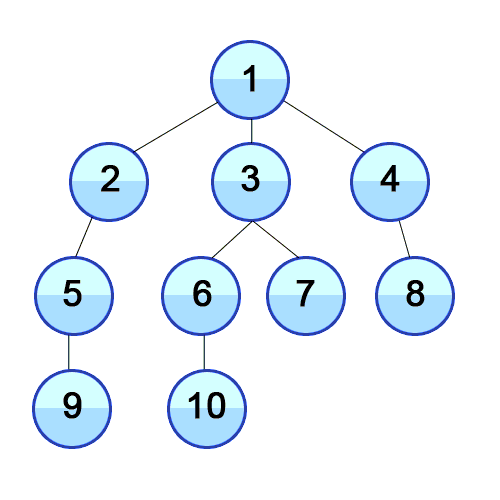
위 그림의 순서를 보면 한 정점에서 방문 뒤 인접한 정점을 다 방문한 후 다음 노드로 방문하는 것을 볼 수 있다.
정의
너비 우선 탐색은 한 정점에서 방문하고 해당 정점과 인접한 정점을 전부 방문한 뒤 다음 인접 정점으로 방문하는 방식이다. 인접한 정점을 전부 방문하면 두번째로 방문했던 정점의 인접 정점을 방문하고 이를 세번째 네번째... n번째 정점 방문을 반복한다.
이전에 방문했던 정점을 불러오기 위해 큐를 사용한다.
구현
dfs 와 마찬가지로 인접 행렬과 인접 리스트로 구현할 수 있으며 시간 복잡도도 같은 이유로 동일하다.
인접한 정점 방문시마다 큐에 저장한 뒤 인접 정점을 다 방문하면 큐에서 정점을 꺼내어 해당 정점에서 인접 정점을 방문한다.
인접 행렬
int visited[MAX_VERTICES]; // 방문 노드 저장
// 인접 행렬 bfs
void bfs_mat(GraphType *g, int v) {
int w;
QueueType q // 큐 정의
init(&q); // 큐 초기화
visited[v] = TRUE; // 정점 v 방문
printf("%d ", v);
enqueue(&q, v); // 큐에 v 삽입
while(!is_empty(&q)) {
v = dequeue(&q); // 큐에서 꺼내기
for(w=0; w < g->n; w++) // 인접 정점 탐색
if(g->adj_mat[v][w] && !visited[w]){
visited[w] = TRUE;
printf("%d ", w);
enqueue(&q, w); // 방문한 정점 큐에 저장
}
}
}인접 리스트
int visited[MAX_VERTICES]; // 방문 노드 저장
// 인접 리스트 bfs
void bfs_list(GraphType *g, int v) {
GraphNode w;
QueueType q // 큐 정의
init(&q); // 큐 초기화
visited[v] = TRUE; // 정점 v 방문
printf("%d ", v);
enqueue(&q, v); // 큐에 v 삽입
while(!is_empty(&q)) {
v = dequeue(&q); // 큐에서 꺼내기
for(w=adj_list[v]; w; w=w->link) // 인접 정점 탐색
if(g->adj_mat[v][w->vertex] && !visited[w]){
visited[w->vertex] = TRUE;
printf("%d ", w->vertex);
enqueue(&q, w->vertex); // 방문한 정점 큐에 저장
}
}
}실제 적용 문제
실제 프로그래머스의 사이트에서 적용된 문제를 간단히 살펴보자.
프로그래머스 - 네트워크
(간단히 리뷰하고자 작성하여 자세한 사항은 링크를 통해 확인해주세요.)
문제 설명
네트워크란 컴퓨터 상호 간에 정보를 교환할 수 있도록 연결된 형태를 의미합니다. 예를 들어, 컴퓨터 A와 컴퓨터 B가 직접적으로 연결되어있고, 컴퓨터 B와 컴퓨터 C가 직접적으로 연결되어 있을 때 컴퓨터 A와 컴퓨터 C도 간접적으로 연결되어 정보를 교환할 수 있습니다. 따라서 컴퓨터 A, B, C는 모두 같은 네트워크 상에 있다고 할 수 있습니다.
컴퓨터의 개수 n, 연결에 대한 정보가 담긴 2차원 배열 computers가 매개변수로 주어질 때, 네트워크의 개수를 return 하도록 solution 함수를 작성하시오.
문제 풀이
문제의 조건에서 연결 정보가 2차원 배열 로 저장 되어 있는 것을 볼 수 있고 연결된 컴퓨터들은 하나의 네트워크로 구성 된다. 연결된 컴퓨터를 한번의 방문 노드로 보고 dfs 를 수행하고 방문하지 않은 정점을 다시 dfs 를 수행하여 매번 dfs 가 새로 수행 될 때마다 하나의 네트워크가 생성된다고 보고 풀이가 가능하다.
파이썬 코드
# 인접 행렬 dfs
def dfs_mat(graph, v, visited):
visited[v] = True
for w in range(len(visited)): # 인접 정점 탐색
if graph[v][w] and not visited[w]:
dfs_mat(graph, w, visited)
def solution(n, computers):
answer = 0
visited = [False for _ in range(n)] # 방문 초기화
for i in range(n):
if visited[i] == False:
answer += 1 # 네트워크 생성
dfs_mat(computers, i, visited) # 네트워크 연결
return answer📕 참고 문헌
참고 링크
Depth-First-Search.gif
Breadth-First-Search-Algorithm.gif
https://currygamedev.tistory.com/10
다음의 책을 참고했습니다.
C언어로 쉽게 풀어쓴 자료구조 [ 개정3판 ]
천인국, 공용해, 하상호 저 | 생능출판사 | 2021년 08월 20일
이것이 취업을 위한 코딩테스트다 with 파이썬
나동빈 저 | 한빛미디어 | 2020년 8월 5일

