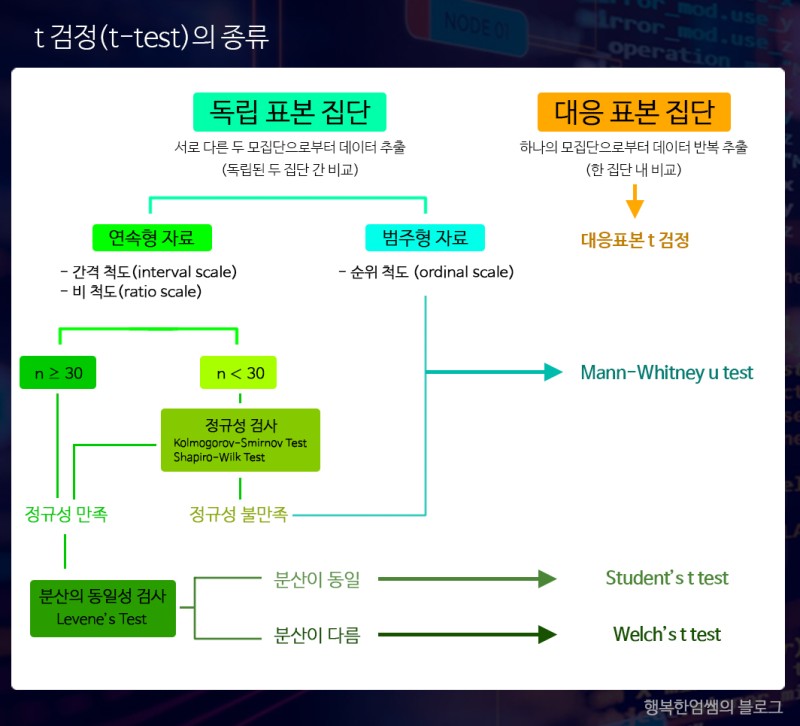
기초 통계
가설이란?
귀무가설(영가설, null hypothesis, H1)
- 가설 검정의 대상
- 기각될 것으로 예상되는 가설
대립가설(anti hypothesis, H0)
채택
기각

간단 정리
- 해당 가설 진실 ≠ 가설 채택 = 해당 가설 기각 근거 충분 X
- 해당 가설 거짓 ≠ 가설 기각 = 해당 가설 기각 근거 있음
왜 이렇게 복잡한가?
- 데이터 수집과 통계 이론에 문제가 없다고 단언할 수 없음
- 참이 아님을 증명하는 것이, 참임을 증명하는 것 보다 쉬움
- 무죄 추정의 원칙
- 피고인이 유죄라고 파악하기 전까지 무죄다(귀무가설)
- 피고인이 유죄라고 파악되면 유죄다(대립가설)
- 연구에 주관성을 개입하면 안됨
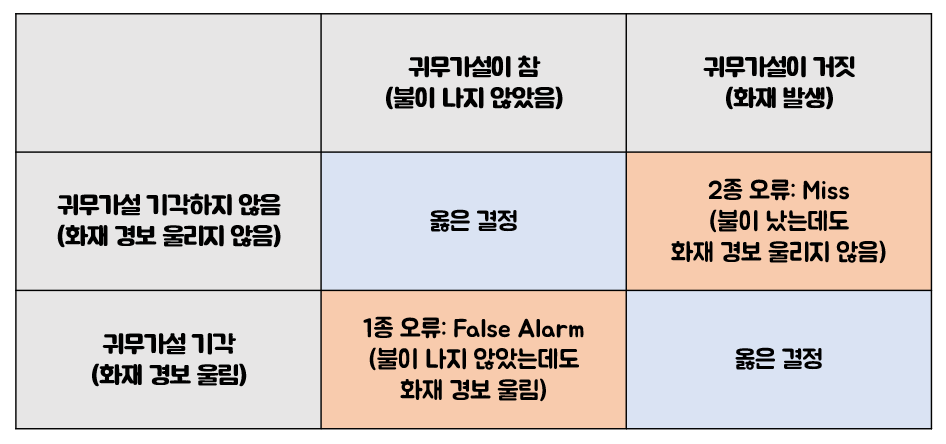
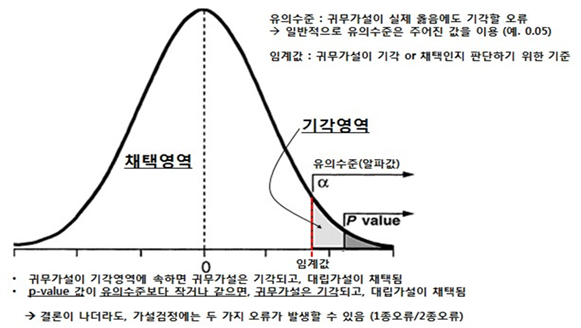
- p-value, p, α 등으로 불림
- 1종 오류를 범할 확률
- 매우 낮을 때, 귀무가설을 기각함
- 보통 [0.05, 0.01, 0.001, 0.0001] 을 기준으로 기각
뜻
조건
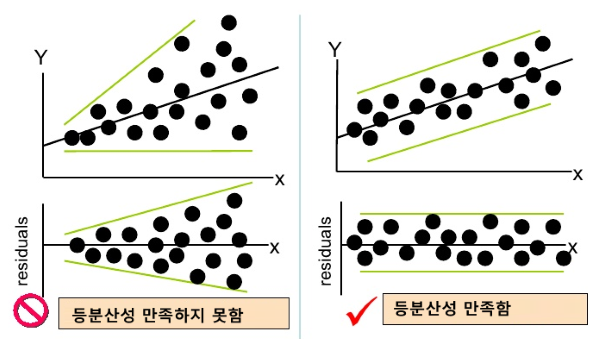
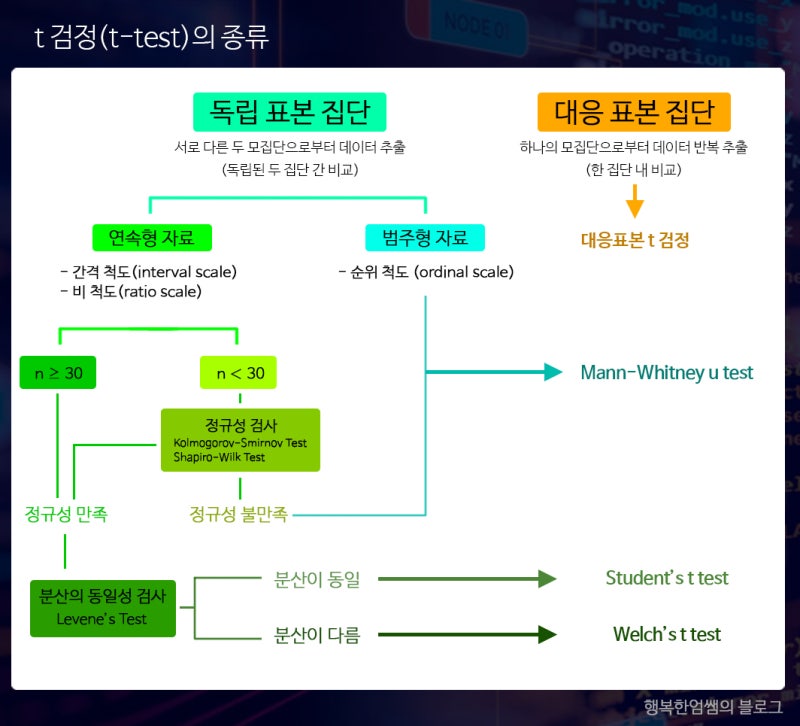
- 위 test는 scipy를 활용하여 확인할 수 있음
실습
데이터 전처리
import pandas as pd
df_fta = pd.read_excel('FTA무역통계_20230109000037.xls',header=4, index_col=1)
for col in df_fta.columns[1:]:
df_fta[col] = pd.to_numeric(df_fta[col].str.replace(',', ''))
pd.concat([df_fta.head(), df_fta.sample(5), df_fta.tail()])
- FTA 데이터에서 수출건수, 수출금액, 수입건수, 수입금액, 무역수지가 각각 평균 이상인 FTA와 평균 미만인 FTA로 이산화를 해 보자
- 이산화 데이터는 df_bin으로 저장한다.
df_fta_bin = df_fta.apply(lambda col : col >= col.mean()).replace([True, False], [1, 0])
df_house = pd.read_csv('서울시 부동산 실거래가 정보.csv', encoding='cp949')
df_house.info()
df_house.loc[:, ['자치구코드','자치구명']].drop_duplicates()
df_house.loc[:, ['법정동코드','법정동명']].drop_duplicates()
df_house.loc[:, ['지번구분','지번구분명']].drop_duplicates()
print(len(df_house), df_house['권리구분'].isnull(), df_house['신고구분'].isnull())
df_house= df_house.columns[len(df_house) * 0.5 > df_house.count()]
df_house.drop(['접수연도','자치구명','법정동명','지번구분명'], inplace=True, axis=1)
print(f'{7.1:0.60f}\n{7.2:0.60f}')
from sklearn.decomposition import PCA
pca = PCA(n_components=3)
reduced = pca.fit_transform(df.iloc[:,1:])
df_reduced = pd.DataFrame(reduced)
threedee = plt.figure().gca(projection='3d')
threedee.scatter(df_reduced[0],df_reduced[1],df_reduced[2])
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
scaled = scaler.fit_transform(df_fta.iloc[:,1:])
df_fta_target = df_fta.apply(lambda row : 'good' if row['무역수지'] > 0 else 'ok' if row['수출건수'] > row['수입건수'] else 'bad', axis=1)
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
lda = LinearDiscriminantAnalysis(n_components=2)
df_fta_lda = lda.fit_transform(scaled, df_fta_target)
pd.DataFrame(df_fta_lda).plot.scatter(x = 0, y = 0)
- PCA, LDA 적용
- 입출력 지원에 문제가 있음
- 용량은 작아야함 (h5 < csv < excel)
- 바이너리등 다양한 파일 format이 있음(찾아봐야할 듯)
T 검정
분포 확인
df_fta['수출건수'].plot.hist()
import numpy as np
np.exp(df_fta['수출건수'])
np.log2(df_fta['수출건수'])
정규성 검사
from scipy import stats
stats.ks_2samp(df_fta['수출건수'], df_fta['수입건수'])
stats.shapiro(df_fta['수출건수']), stats.shapiro(df_fta['수입건수'])
stats.probplot(df_fta.['수출건수'], plot = plt)
등분산성 검사
stats.levene(df_fta['수출건수'], df_fta['수입건수'])
T-Test
stats.ttest_ind(df_fta['수출건수'], df_fta['수입건수'])
stats.ttest_ind(df_fta['수출건수'], df_fta['수입건수'], equal_var=False)
stats.ttest_rel(df_fta['수출건수'], df_fta['수입건수'])
man-whitney u
stats.mannwhitneyu(df_fta['수출건수'], df_fta['수입건수'])
stats.wilcoxon(df_fta['수출건수'], df_fta['수입건수'])
자동화 코드
한국어 plot
import matplotlib.pyplot as plt
import matplotlib as mpl
plt.rc('font', family='NanumBarunGothic')
mpl.rcParams['axes.unicode_minus'] = False
정규성 검사
import matplotlib.pyplot as plt
from scipy import stats
import pandas as pd
import numpy as np
def df_plot_set(columns, size=None):
if size:
if size[0] * size[1] < len(columns):
raise Exception('크기를 맞춰주세요')
fig, axes = plt.subplots(size[1], size[0], figsize=(size[0] * 6, size[1] * 4))
else:
fig, axes = plt.subplots(1, len(columns), figsize=(len(columns) * 6, 4))
return fig, axes
def df_plot_show(title, data_len, func, param:dict, axes, loc, size=None):
none_key = [k for k, v in param.items() if type(v) == type(None)][0]
if size and size.count(1) == 0:
param[none_key] = axes[loc//size[0]][loc%size[0]]
elif data_len != 1:
param[none_key] = axes[loc]
else:
param[none_key] = axes
func(**param)
param[none_key].set_title(title)
def one_normality_test(df:pd.DataFrame, threshold:float=0.05, size=None):
print('one_normality_test')
check_list = []
columns = df.columns
print(columns)
fig, axes = df_plot_set(columns, size)
for i, col in enumerate(columns):
series = df[col].dropna()
df_plot_show(col,len(columns),stats.probplot,
{
'x':series,
'plot':None,
},
axes,i,size)
if 30 < series.count():
print(f'{col}은 30보다 큼으로 정규성을 만족함')
check_list += [False]
continue
if len(series) < 3:
check_list += [True]
continue
p_val = stats.shapiro(series).pvalue
level = (p_val < np.array([0.05, 0.01, 0.001, 0.0001])).sum()
if p_val < threshold:
print(f'{col}은 p_value가 {p_val:0.4f}임으로 정규성을 만족하지 않음', '*' * level)
check_list += [True]
else:
print(f'{col}은 p_value가 {p_val:0.4f}임으로 정규성을 만족', '*' * level)
check_list += [False]
return df.columns[check_list]
def two_normality_test(df:pd.DataFrame, threshold:float=0.05):
print('two_normality_test')
data = {
'col1':[],
'col2':[],
'kstest_p_val':[],
'normality_result':[],
}
for col1 in df.columns:
for col2 in df.columns:
if col1 == col2:
break
p_val = stats.kstest(df[col1].dropna(), df[col2].dropna()).pvalue
level = (p_val < np.array([0.05, 0.01, 0.001, 0.0001])).sum()
data['col1'] += [col1]
data['col2'] += [col2]
data['kstest_p_val'] += [p_val]
if p_val < threshold:
print(f'{col1}과 {col2}의 p_value가 {p_val:0.4f}임으로 두 분포가 동일하지 않음', '*' * level)
data['normality_result'] += ['mann-whitney u']
else:
print(f'{col1}과 {col2}의 p_value가 {p_val:0.4f}임으로 두 분포가 동일함', '*' * level)
data['normality_result'] += ['levene']
return pd.DataFrame(data)
def equal_variance_test(df:pd.DataFrame, df_result:pd.DataFrame, threshold:float=0.05):
print('equal_variance_test')
df_cols = df_result.loc[df_result['normality_result'] == 'levene', ['col1', 'col2']]
df_result['levene_p_val'] = df_cols.apply(lambda row:stats.levene(df[row['col1']].dropna(),df[row['col2']].dropna()).pvalue, axis=1)
level = (df_result['levene_p_val'].to_numpy() < np.array([0.05, 0.01, 0.001, 0.0001]).reshape(-1, 1)).sum(axis=0)
df_result['equal_variance_result'] = None
for idx in df_cols.T:
col1, col2, p_val = df_result.loc[idx, 'col1'], df_result.loc[idx, 'col2'], df_result.loc[idx, 'levene_p_val']
if p_val < threshold:
print(f'{col1}과 {col2}의 p_value가 {p_val:0.4f}임으로 분산이 동일한 모집단에서 추출하지 않음', '*' * level[idx])
df_result.loc[idx, 'equal_variance_result'] = 'whlch_t_test'
else:
print(f'{col1}과 {col2}의 p_value가 {p_val:0.4f}임으로 분산이 동일한 모집단에서 추출', '*' * level[idx])
df_result.loc[idx, 'equal_variance_result'] = 'student_t_test'
def ttest_test(df:pd.DataFrame, df_result:pd.DataFrame, threshold:float=0.05):
print('ttest_test')
df_cols = df_result.loc[df_result['equal_variance_result'].notnull(), ['col1', 'col2', 'equal_variance_result']]
df_result['ttest_p_val'] = df_cols.apply(lambda row:stats.ttest_ind(df[row['col1']].dropna(),df[row['col2']].dropna(), equal_var= row['equal_variance_result'] == 'student_t_test').pvalue, axis=1)
level = (df_result['ttest_p_val'].to_numpy() < np.array([0.05, 0.01, 0.001, 0.0001]).reshape(-1, 1)).sum(axis=0)
df_result['diff_stats_test'] = None
for idx in df_cols.T:
col1, col2, p_val = df_result.loc[idx, 'col1'], df_result.loc[idx, 'col2'], df_result.loc[idx, 'ttest_p_val']
if p_val < threshold:
print(f'{col1}과 {col2}의 p_value가 {p_val:0.4f}임으로 동일한 평균(예상) 값을 갖지 않는다', '*' * level[idx])
df_result.loc[idx, 'diff_stats_test'] = '다름'
else:
print(f'{col1}과 {col2}의 p_value가 {p_val:0.4f}임으로 동일한 평균(예상) 값을 갖는다', '*' * level[idx])
df_result.loc[idx, 'diff_stats_test'] = '같음'
def mannwhitneyu_test(df:pd.DataFrame, df_result:pd.DataFrame, threshold:float=0.05):
print('mannwhitneyu_test')
df_cols = df_result.loc[df_result['normality_result'] == 'mann-whitney u', ['col1', 'col2']]
df_result['mannwhitneyu_p_val'] = df_cols.apply(lambda row:stats.mannwhitneyu(df[row['col1']].dropna(),df[row['col2']].dropna()).pvalue, axis=1)
level = (df_result['mannwhitneyu_p_val'].to_numpy() < np.array([0.05, 0.01, 0.001, 0.0001]).reshape(-1, 1)).sum(axis=0)
for idx in df_cols.T:
col1, col2, p_val = df_result.loc[idx, 'col1'], df_result.loc[idx, 'col2'], df_result.loc[idx, 'mannwhitneyu_p_val']
if p_val < threshold:
print(f'{col1}과 {col2}의 p_value가 {p_val:0.4f}임으로 동일한 평균(예상) 값을 갖지 않는다', '*' * level[idx])
df_result.loc[idx, 'diff_stats_test'] = '다름'
else:
print(f'{col1}과 {col2}의 p_value가 {p_val:0.4f}임으로 동일한 평균(예상) 값을 갖는다', '*' * level[idx])
df_result.loc[idx, 'diff_stats_test'] = '같음'
def result_plot_show(df, df_target, size=None):
df_target = df_target.T
fig, axes = df_plot_set(df_target.columns, size)
for i, idx in enumerate(df_target):
col1, col2 = df_target[idx]
df_plot_show(f'{col1} {col2}',len(df_target),sns.histplot,
{
'data':df[[col1, col2]],
'kde':True,
'ax':None,
},
axes,i,size)
def check_size(len_df):
n = int(len_df ** 0.5)
for i in range(n, 0, -1):
if len_df % i == 0:
break
return (i,len_df//i)
def auto_ttest(df):
size = check_size(len(df.columns))
columns_not_normality = one_normality_test(df, size=size)
df_result = two_normality_test(df)
equal_variance_test(df, df_result)
ttest_test(df, df_result)
mannwhitneyu_test(df, df_result)
df_target = df_result.loc[df_result['diff_stats_test'] == '다름', ['col1', 'col2']]
size = check_size(len(df_target.index))
result_plot_show(df, df_target, size=size)
return df_result
회고
- 함부로 자동화 코드를 만들지 말자..
- 입력값의 형태는 각 비교하고자 하는 객체를 컬럼에 넣어서 비교하면 됨
- 자동화 코드는 기본적으로 ind인 경우를 상정하여 제작하였음
Ref