삼각함수란 ?
- 수학에서의 삼각함수는 직각 삼각형의 각을 직각 삼각형 변들의 길이 비로 나타내는 함수
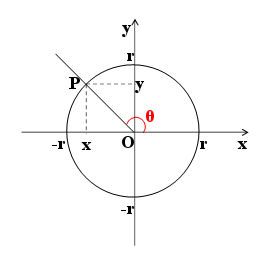
- 게임 개발을 하는 관점에서는 각도를 이용할 때 삼각함수를 이용하면 아주 좋다.
ㄴ ex) 발사체의 각도 / 캐릭터의 대각선 이동 / 스킬 범위 설정 등등
▷ 삼각함수를 하면 기억할 3가지
빗변 : l <-> 대변(높이): h <-> 밑변: b
-
사인 (sin)
-
사인은 빗변 (제일 긴)과 높이 (대변)의 비율을 구해주는 함수
-
sin Φ(각) = 대변 / 빗변 = h / l
-
-
코사인 (cos)
-
빗변과 밑변의 비율을 계산해주는 함수
-
cos Φ(각) = 밑변 / 빗변 = b / l
-
-
탄젠트 (tan)
-
직각 삼각형에서 어떠한 각도를 넣었을 때 밑변과 대변(수직인 변)의 비율을 정해준다.
-
tan (45) = 1
-
tan Φ(각) = 대변 / 밑변 = h / b
-
▶ 프로그래밍에서의 삼각함수
-
API 에서는 윈도우 좌표계를 사용한다.
-
윈도우 좌표계는 데카르트 좌표계와는 달리 Y축이 아래로 내려갈수록 증감이 되기 때문에 Y축 좌표를 구할때는 별다른 처리를 하지 않았다면 sin 앞쪽에 "-" 기호를 붙인다.
▷ 기억해야할 개념
-
호도법
- 각도를 나타내는 표현 방법 중 하나로 호의 길이로 각도를 표기하는 방법
- PI를 사용해 180도 각도를 표시하는 것
- 컴퓨터는 각도를 인식할 때 도를 사용할 수가 없다.
- 반지름의 길이와 같은 호에 대한 중심각 1호도 (라디안)라고 부른다.
-
라디안
- 호도법을 표기할 때 사용하는 단위
- 반지름과 호의 길이가 같은 값을 1라디안이라고 정의한다.
- 1 라디안 = 57.3도
-
도
- 일반적으로 사용하는 각의 단위(각도)
- 도수법 / 각도 표기라고 불린다.
- 한바퀴를 360도로 정의한다.
-
60 분법
- 원의 둘레를 360등분하여 각의 크기를 나타내는 방법
- PI(원주율) : 3.14
- 원의 둘레 : 2x PI x 반지름
- 원의 넓이 : 반지름 x 반지름 x PI
※ PI의 라디안 값은 180도
-
아래와 같은 공식이 성립할 수 있다.
-
Degree
ㄴ 180 Degree = PI Radian
ㄴ 1 Degree = PI / 180 Radian
ㄴ x Degree = x * PI / 180 Radian
- Radian
ㄴ PI Radian = 180 Degree
ㄴ 1 Radian = 180 / PI Degree
ㄴ x Radian = x * 180 / PI Degree
※ 부채꼴 모양에서 반지름, 호, 중심각 3가지 중에 2개를 알 수 있다면 나머지 1개도 구할 수 있다.
▷ 기본 공식
- 두점 사이의 거리
ㄴ 두점을 안다 (Start / End) -> 서로의 거리를 안다 -> 목표 지점에서 시작 지점을 뺀다.
ㄴ End - Start = 두 점 사이의 거리 -> 뺀 만큼의 차
- 위 공식으로 각점 (X,Y) 사이의 델타량을 구한다.
ㄴ DeltaX, DeltaY
-
대각선 (빗변)의 거리
ㄴ Distance (빗변) = sqrt (DeltaX DeltaX + DeltaY DeltaY);
ㄴ sqrt(): x의 제곱근 값을 구하기 위한 함수 -
각을 구한다. (공식을 사용하자)
float angle = acos(DeltaX / Distance);
ㄴ 삼각 함수: 각도를 넣어서 각도 계산
ㄴ 역삼각 함수: 결과 값을 넣어서 각도를 계산
ㄴ 역삼각 함수는 arc or a를 표기
-
각도에 대한 변이량을 구한다.
- float DeltaX = cos(Radian) * Distance (이동량);
- float DeltaY = -sin(Radian) * Distance (이동량);
- x축 좌표 구하기
- x = cos(각도 PI / 180) 속도;
- y축 좌표 구하기
- y = -sin(각도 PI / 180) 속도;