방학을 맞아 새로운 프로젝트를 시작해서 관련해서 정리해보겠습니다,,
원래 백엔드 포지션으로 개발 2번정도 했었는데 프론트엔드 포지션도 경험해보고 싶어서 이번에는 프론트엔드 포지션으로 처음 맡아서 진행하게 되었어요.
아직 디비나 테이블이 완성되지 않아서 지금은 웹퍼블리싱만 하고 있습니다.
그리고 코드트리에서 기본문제부터 풀어가고 있어요 ㅎㅎ 대학교 1학년 수준이라 하루에 30개정도 빠르게 풀어나가는 중,, 기초문제 빠르게 다 풀고 자료구조랑 알고리즘으로 넘어가려구요 ㅋㅋㅋㅋ 그래서 결론은 기초문제중에서 좀 막혔던 문제 풀이랑 웹퍼블리싱하는데 막혔던 부분에 대해서 정리해서 블로그에 쓸 예정입니다! 그리고 자료구조 공부중인데 자료구조 공부한 내용 정리도 포함될꺼같아요!서론이 좀 길었는데 다음 게시물부터는 코드 정리 및 설명만 쓸 예정이에요.

그럼 일단 코드트리 문제 중 어려웠던 내용이 없어서 자료구조 공부한 내용 정리부터 시작하겠습니다.

Chapter 01. 자료구조와 알고리즘의 이해

1-1 자료구조에 대한 기본적인 이해

1. 선형구조 - 리스트, 스택, 큐
2. 비선형구조 - 트리, 그래프
3. 파일구조 - 순차파일, 색인파일, 직접파일
4. 단순구조 - 정수, 실수, 문자, 문자열

이렇게 분류할 수 있는데 이 교재에서는 선형 자료구조와 비선형 자료구조를 다룬다.

1-2 알고리즘의 성능분석 방법

시간 복잡도 - 속도에 해당하는 알고리즘의 수행시간 분석결과

공간 복잡도 - 메모리 사용량에 대한 분석결과

최적의 알고리즘이란 메모리를 적게 쓰고 속도도 빨라야하지만 일반적으로 알고리즘을 평가할때는 메모리의 사용량보다 실행속도에 초점을 둔다. 즉 시간 복잡도가 굉장히 중요함.

따라서 시간 복잡도를 구하는 방식이 중요한데 알고리즘의 수행속도를 평가할 때는 다음과 같은 방식을 취한다

“연산의 횟수를 셉니다.”

“그리고 처리해야할 데이터의 수 n에 대한 연산횟수의 함수 T(n)을 구성합니다.”

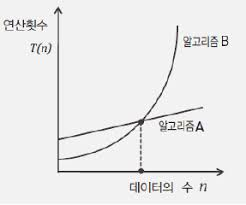
위의 그림은 동일한 기능을 제공하는 서로 다른 두 알고리즘의 성능을 비교한 결과이다.

데이터의 수가 작을때는 알고리즘 B 가 효율이 좋고 데이터의 수가 클때는 알고리즘 A 의 효율이 좋은데 보통 데이터의 수가 많다고 가정하고 판단하기 떄문에 알고리즘 A 만 사용하고 알고리즘 B 는 쓸모 없다고 생각할 수 있으나 A와 같이 안정적인 성능을 보장하는 알고리즘은 B와 같은 성격의 알고리즘에 비해 구현의 난이도가 높은 편이기 때문에 알고리즘B 를 선택하기도 한다. 따라서 상황에 맞게 알고리즘을 짜는게 굉장히 중요하다!!

순차 탐색 알고리즘

//
//  1065.cpp
//  
//
//  Created by 이승섭 on 2023/06/30.
//

#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;

int main(){
    int x;
    int cnt = 0;
    int num = 100;
    cin >> x;
    if(x <= 99){
        cout << x << '\n';
        return 0;
    }
    else{
        while(num <= x){
            int first = num / 100;
            int second = (num - first*100) / 10;
            int third = num - (first * 100 + second * 10);
            if((first - second) == (second - third)){
                cnt++;
            }
            num++;
        }
        cout << 99+cnt << '\n';
        return 0;
    }
}

위의 코드는 백준 1065번 한수에 대한 코드이다. 100부터 입력하는 수까지 1씩 증가하면서 카운트를 하는 방식으로 시간 복잡도는 T(n) = n 이 된다.

이진 탐색 알고리즘

//
//  2805.cpp
//
//
//  Created by 이승섭 on 2023/06/29.
//

#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;

long n,m;
vector<long> tree;

int main(){
    cin >> n;
    cin >> m;
    for(int i = 0; i < n; i++){
        long x;
        cin >> x;
        tree.push_back(x);
    }
    
    sort(tree.begin(), tree.end());
    
    int start = 0;
    long end = tree[n-1];
    long result,sum;
    
    while(start <= end){
        sum = 0;
        long mid = (start + end) / 2;
        for(auto i = 0; i < n; i++){
            if(mid > tree[i]){
                sum += 0;
            }
            else{
                sum = sum + (tree[i] - mid);
            }
        }
        if(m == sum) {
            result = mid;
            break;
        }
        else if(m > sum){
            end = mid - 1;
        }
        else{
            result = mid;
            start = mid + 1;
        }
    }
    cout << result;
}

위의 코드는 백준 2805번 나무자르기에 해당하는 코드이다. 처음에 배열의 길이에 해당하는 수와 가져가야할 나무의 길이를 입력받고 그 다음에 배열을 입력받는다. 이진 탐색 알고리즘에서 가장 중요한 조건인 정렬을 해주고 0부터 가장 큰 길이의 나무까지 이진탐색 알고리즘을 이용해 최적의 답을 찾는 문제이다. 이진 탐색 알고리즘은 순차탐색 알고리즘보다 훨신 좋은 성능을 보이며 이진 탐색 알고리즘의 시간 복잡도는 T(n) = log2n이 된다.

시간 복잡도는 항상 Worst case(최악의 경우)로 계산을 해야한다.

첫번째 이유 - 데이터가 많아질 수록 연산의 수가 기하급수적으로 늘어날 수 있다.

두번째 이유 - 사실 최악, 최선의 경우보다 평균적의 경우로 구하는게 가장 올바르지만 Average case 는 구하는방식이 굉장히 복잡하고 아예 못 구하는 경우가 생긴다.

빅-오 표기법(Big-Oh Notation)

빅-오라는 것은 함수 T(n)에서 가장 영향력이 큰 부분이 어딘가를 따지는 것이다.

다음과 같은 수식에서 빅 오는 O(n^2)이 된다.

“T(n)이 다항식으로 표현이 된 경우, 최고차항의 차수가 빅-오가 된다.”

대표적인 빅-오

• O(1) - 상수형 빅-오라 하며, 데이터 수에 상관 없이 연산횟수가 고정인 유형의 알고리즘을 뜻한다.
• O(log n) - 로그형 빅-오라 하며, 데이터 수의 증가율에 비해 연산횟수의 증가율이 훨씬 낮은 알고리즘을 뜻한다.
• O(n) - 선형 빅-오라 하며, 데이터의 수와 연산횟수가 비례하는 알고리즘을 의미한다.
• O(n log n) - 선형로그형 빅-오라 하며, 데이터의 수가 2배로 늘 때, 연산횟수는 2배를 조금 넘게 증가하는 알고리즘을 의미한다.
• O(n^2) - 데이터 수의 제곱에 해당하는 연산횟수를 요구하는 알고리즘을 의미한다. 따라서 데이터의 양이 많은 경우 적용하기 부적절하다. 이중으로 중첩된 반복문 내에서 알고리즘에 관련된 연산이 진행되는 경우 발생한다.
• O(n^3) - 데이터 수의 세 제곱에 해당하는 연산횟수를 요구하는 알고리즘을 의미한다. 이는 삼중으로 중첩된 반복문 내에서 알고리즘에 관련된 연산이 진행되는 경우에 발생한다.
• O(2^n) - 지수형 빅-오라 하며, 사용하기에 매우 무리가 있는, 사용한다는 것 자체가 비현실적인 알고리즘이다. 처음 알고리즘을 개발했을 때 이러한 성능을 보인다면, 개선의 과정을 거쳐서 현실적인 연산횟수를 보이는 알고리즘으로 수정되어야 한다.

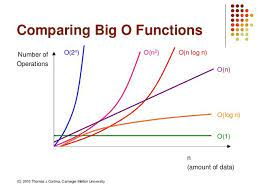
위의 표는 대표적인 빅-오의 데이터 수의 증가에 따른 연산횟수의 증가율을 그래프로 정리한 것이다.