승섭 7/18

Chapter 02. 재귀(Recursive)
재귀함수(Recursive Function) 란 함수 내에서 자기 자신을 다시 호출하는 함수를 의미한다.

void Recursive(void)

{
	printf("Recursive call! \n");
	Recursive(); // 나! 자신을 재호출한다.
}

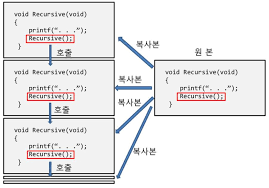
위의 그림이 재귀함수의 호출을 설명하는데 재귀함수가 호출되면, 재귀함수의 복사본이 만들어져서 복사본이 실행되는 구조로 재귀함수의 호출을 설명하고 있다.
또한 재귀함수는 반복문과 똑같이 “재귀의 탈출조건” 이 무조건 들어가 있어야한다.
재귀함수를 사용하는 가장 대표적인 예시로 피보나치수열 과 하노이타워가 있는데 백준 문제를 풀어보면서 해결해보겠다. 재귀함수를 사용하는데 있어서 많은 문제를 풀어보면서 감을 잡아야 하는게 필요하다고 생각하고 재귀적으로 사고하면서 해결해 나가는게 무엇보다 중요하다.

백준 10870 피보나치 수 5
//
//  10870.cpp
//  
//
//  Created by 이승섭 on 2023/07/18.
//

#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;

int fibo(int a){
    if(a == 1){
        return 1;
    }
    if(a == 0){
        return 0;
    }
    return fibo(a-1) + fibo(a-2);
}

int main(){
    int x;
    cin >> x;
    cout << fibo(x) << '\n';
}

​
위의 예제는 재귀함수를 이용해 푸는 대표적인 문제라고 할 수 있는데 탈출 조건을 a == 1 일때 1을 반환하고 a == 0 일때 0을 반환하는 방식으로 설정하고 피보나치 수열은 만약 3이면 1과 2를 더해주고 4면 2 와 3을 더해주는 수열이므로 return fibo(a-1) + fibo(a-2) 를 통해 재귀적으로 문제를 해결할 수 있다.

백준 1914 하노이탑
//
//  1914.cpp
//
//
//  Created by 이승섭 on 2023/07/18.
//

#include <iostream>
#include <vector>
#include <algorithm>
#include <cmath>
#include <string>

using namespace std;

void hanoi(int a, int from, int by, int to){
    if(a == 1){
        cout << from << ' ' << to << '\n';
    }
    else{
        hanoi(a-1, from, to, by);
        cout << from << ' ' << to << '\n';
        hanoi(a-1, by, from, to);
    }
}

int main(){
    int x;
    cin >> x;
    string count = to_string(pow(2,x));
    int point = count.find('.');
    count = count.substr(0, point);
    count[count.length()-1] -= 1;
    cout << count << '\n';
    if(x <= 20){
        hanoi(x, 1, 2, 3);
    }
}

​
위의 예제는 재귀 함수를 활용하는 대표적 예제중 하나인 하노이 탑 문제이다. 교재에도 하노이 탑 예제가 나와있는데 재귀 함수를 이용해 문제를 풀 때에는 일련의 과정을 반복하는 것을 확인해야 하는데 하노이 탑에서는 3가지 과정이 반복된다고 볼 수 있다. 3개의 원반을 a에서 c로 옮길 때 가장 큰 원반을 제외한 2개의 원반을 b로 옮기고 가장 큰 원반을 c로 옮긴 후 나머지 2개의 원반을 c로 옮기는 과정을 반복해야한다.
맨 아래의 원반을 제외한 나머지 원반을 A에서 B로 이동
큰 원반 1개를 A에서 C로 이동
작은 원반들을 B에서 C로 이동
이 3가지의 과정을 코드로 바꾼 내용이
hanoi(a-1, from, to, by);
cout << from << ' ' << to << '\n';
hanoi(a-1, by, from, to);
​
다음에 해당하는 내용이며 이동해야 할 원반의 수가 1이면 그냥 c로 옮기면 되므로
if(a == 1){
cout << from << ' ' << to << '\n';
}
​
위의 코드가 재귀함수의 탈출 조건이 된다.
따라서 재귀 함수의 탈출 조건과 반복되는 코드를 만들었으므로 하노이 탑 문제를 해결했다고 볼 수 있다. 하지만 문제의 조건에서 20개의 원반까지는 원반의 이동 과정을 출력해야 되며 20~100개의 원반은 이동 횟수만 출력해야하는데 원반의 이동 횟수를 점화식으로 나타내면

이 되는데 따라서 x에 100이 들어가면 가장 큰 타입인 long long 으로도 표현을 할 수가 없다.
따라서 원반 이동횟수를 string으로 표현해야하는데 이때 pow()를 쓰면 소수점까지 string으로 들어가기 때문에
문자열 자르기인 substr() 을 이용해 ‘.’ 부터 나오는 문자열을 잘라주면 해결 가능하다.
그 다음 문자열 마지막 숫자에 -1을 해주어 표현하면 코드가 완성된다.

백준 9184 신나는 함수 실행
//
//  9184.cpp
//  
//
//  Created by 이승섭 on 2023/07/18.
//

#include <iostream>
#include <vector>
#include <algorithm>
#include <cmath>
#include <string>

using namespace std;

int store[21][21][21];

int solve(int a, int b, int c){
    if(a <= 0 || b <= 0 || c <= 0){
        return 1;
    }
    if(a > 20 || b > 20 || c > 20){
        return solve(20, 20, 20);
    }
    if(store[a][b][c]){
        return store[a][b][c];
    }
    if(a < b && b < c){
        store[a][b][c] =  solve(a, b, c-1) + solve(a, b-1, c-1) - solve(a, b-1, c);
        return store[a][b][c];
    }
    else{
        store[a][b][c] =  solve(a-1, b, c) + solve(a-1, b-1, c) + solve(a-1, b, c-1) - solve(a-1, b-1, c-1);
        return store[a][b][c];
    }
}

int main(){
    int a, b, c;
    cin >> a >> b >> c;
    while(!(a == -1 && b == -1 && c == -1)){
        cout << "w(" << a << ", " << b << ", " << c << ") = " << solve(a,b,c) << '\n';
        cin >> a >> b >> c;
    }
    return 0;
}

​
위의 문제는 이미 문제에 재귀적인 알고리즘이 완성되어 있고 그대로 복사하기만 하면 된다. 단 문제점으로 그저 단순히 따라하기만 하면 숫자가 커질 수록 매우 오랜 시간이 걸리게 된다. 따라서 다른 방법 한가지를 추가해야하는데 그게 바로 메모리제이션이다.
메모이제이션은 재귀와 재귀를 사용하는 DFS, 동적 계획법과 같은 곳에서 많이 사용하는 방법으로, 이미 연산한 내용에 대해 중복 연산을 수행하지 않도록 도와주기 때문에 연산 속도를 향상시킬 수 있다.
이 메모이제이션을 적용하기 위해 (a, b, c)를 표시할 수 있는 3차 배열을 하나 정했고, 이외의 내용들은 조건에 해당하는 return 값을 주면서 재귀를 진행하면 문제를 풀 수 있다.

백준 4779 칸토어집합
//
//  6603.cpp
//  
//
//  Created by 이승섭 on 2023/07/18.
//

#include <iostream>
#include <vector>
#include <algorithm>
#include <cmath>

using namespace std;

void line(int a){
    int space = pow(3,(a-1));
    int b = 0;
    if(a == 0){
        cout << '-';
    }
    else{
        line(a-1);
        while(b != space){
            cout << ' ';
            b++;
        }
        line(a-1);
    }
}

int main(){
    int x;
    while(cin >> x){
        line(x);
        cout << '\n';
    }
}

​
위의 문제는 복잡한 재귀적 사고를 거치지는 않는 단순한 문제이다. 만약 3을 입력하면 앞뒤로 재귀함수 2를 출력하고 가운데에 3^(3-1) 즉 9개의 공백을 출력하는 문제이다.
막힌 부분은 바로 파일 입출력 부분인데, 메인 함수 안의 반복문에 조건으로 입력을 넣어줌으로서 입력이 끝날때까지 무한 루프 안에서 돌리는 방식으로 진행된다.

출처 - 윤성우의 열혈 자료구조(Chapter 02 - 재귀)