승섭 7/23

섭승이·2023년 7월 23일
개발일기자료구조
0

자료구조

목록 보기
7/12
post-custom-banner

Chapter 08. 트리(Tree)

트리의 개요

“트리는 계층적 관계를 표현하는 자료구조이다”

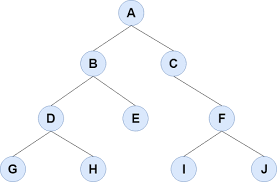
트리와 관련된 기본적인 용어

  • 노드: node ⇒ 트리의 구성요소에 해당하는 A,B,C,D,E 와 같은 요소

  • 간선: edge ⇒ 노드와 노드를 연결하는 연결선

  • 루트 노드: root node ⇒ 트리 구조에서 최상위에 존재하는 A와 같은 노드

  • 단말 노드: terminal node ⇒ 아래로 또 다른 노드가 연결되어 있지 않은 G, H, I, J 같은 노드

  • 내부 노드: internal node ⇒ 단말 노드를 제외한 모든 노드로 A, B, C, D, E, F와 같은 노드

  • 부모 노드: parent node ⇒ 노드 A 는 노드 B, C 의 부모 노드

  • 자식 노드: children node ⇒ 노드 B, C 는 노드 A의 자식 노드

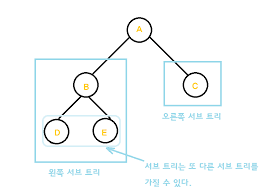
    서브 트리 : 큰 트리에 속하는 작은 트리

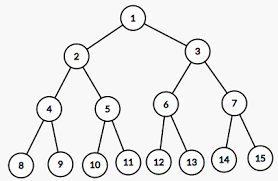
    이진 트리 : 자식 노드가 두 개씩 달린 노드

  • 루트 노드를 중심으로 두 개의 서브 트리로 나뉘어진다.

  • 나뉘어진 두 서브 트리도 모두 이진 트리이어야 한다.

  • 노드가 위치할 수 있는 곳에 노드가 존재하지 않는다면 공집합 노드가 존재하는 것으로 간주한다. 물론 공집합 노드도 이즌 트리의 판단에 있어서 노드로 인정한다.

이진 트리는 크게 포화 이진 트리와 완전 이진 트리로 나뉘어진다.

위의 그림이 포화 이진 트리로 모든 레벨이 꽉 찬 이진 트리이다.

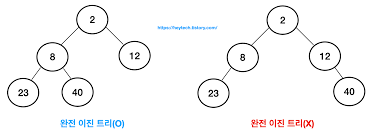
완전 이진 트리란 위의 그림에서 볼 수 있듯이 포화 이진 트리처럼 모든 레벨이 꽉 찬 상태는 아니지만, 차곡차곡 빈 틈 없이 노드가 채워진 이진 트리를 뜻한다.

위의 그림 중 오른쪽 노드는 공집합 노드가 존재하는 것으로 간주되므로 이진 트리는 맞지만 완전 이진 트리는 아니다.

이진 트리의 구현

이진 트리 역시 배열을 기반으로도, 연결 리스트를 기반으로도 구현이 가능하지만, 트리를 표현하기에는 연결 리스트가 더 유연하기 때문에 우리가 구현할 대부분의 트리는 연결 리스트를 기반으로 구현한다.

이진 트리 자료구조의 ADT

  • BTreeNode * MakeBTreeNode(void);
    • 이진 트리 노드를 생성하여 그 주소 값을 반환한다.
  • BTData GetData(BTreeNode * bt);
    • 노드에 저장된 데이터를 반환한다.
  • void SetData(BTreeNode * bt, BTData data);
    • 노드에 데이터를 저장한다. data로 전달된 값을 저장한다.
  • BTreeNode GetLeftSubTree(BTreeNode bt);
    • 왼쪽 서브 트리의 주소 값을 반환한다.
  • BTreeNode GetRightSubTree(BTreeNode bt);
    • 오른쪽 서브 트리의 주소 값을 반환한다.
  • void MakeLeftSubTree(BTreeNode main, BTreeNode sub);
    • 왼쪽 서브 트리를 연결한다.
  • void MakeRightSubTree(BTreeNode main, BTreeNode sub);
    • 오른쪽 서브 트리를 연결한다.

위의 ADT를 토대로 구현한 이진 트리 코드이다.

#include <stdio.h>
#include <stdlib.h>
#include "BinaryTree.h"

// 이진 트리 노드를 생성하고 그 주소 값을 반환한다.
BTreeNode * MakeBTreeNode(void)
{
	BTreeNode * nd = (BTreeNode*)malloc(sizeof(BTreeNode));

	nd->left = NULL;
	nd->right = NULL;
	return nd;
}

// 노드에 저장된 데이터를 반환한다.
BTData GetData(BTreeNode * bt)
{
	return bt->data;
}

// 노드에 함수의 파라미터로 받은 데이터를 저장한다.
void SetData(BTreeNode * bt, BTData data)
{
	bt->data = data;
}

// 왼쪽 서브 트리의 주소 값을 반환한다.
BTreeNode * GetLeftSubTree(BTreeNode * bt)
{
	return bt->left;
}

// 오른쪽 서브 트리의 주소 값을 반환한다.
BTreeNode * GetRightSubTree(BTreeNode * bt)
{
	return bt->right;
}

// 왼쪽 서브트리를 연결한다.
void MakeLeftSubTree(BTreeNode * main, BTreeNode * sub)
{
	if(main->left != NULL)
		free(main->left);

	main->left = sub;
}

// 오른쪽 서브트리를 연결한다.
void MakeRightSubTree(BTreeNode * main, BTreeNode * sub)
{
	if(main->right != NULL)
		free(main->right);

	main->right = sub;
}

여기서 맨 아래 2개의 함수를 구현할 때 “왼쪽 또는 오른쪽 서브 트리가 존재한다면, 해당 트리를 삭제하고서 새로운 왼쪽 또는 오른쪽 서브 트리를 연결한다” 라는 특징을 기억해두어야 한다.

위와 같은 방법을 사용하면 한번의 free 함수 호출이 전부이기 때문에, 삭제할 서브 트리가 하나의 노드로 이루어져 있다면 문제되지 않지만, 그렇지 않다면 메모리의 누수로 이어진다.

따라서 둘 이상의 노드로 이뤄져 있는 서브 트리를 완전히 삭제하려면 서브 트리를 구성하는 모든 노드를 대상으로 free함수를 호출해야하는데 이를 가리켜 “순회”라고 한다.

이진 트리의 순회(Traversal)

이진 트리를 대상으로 하는 대표적인 순회의 세 가지 방법은 다음과 같다.

  • 전위 순회(Preorder Traversal) → 루트 노드를 먼저
  • 중위 순회(Inorder Traversal) → 루느 토드를 중간에
  • 후위 순회(Postorder Traversal) → 루트 노드를 마지막에

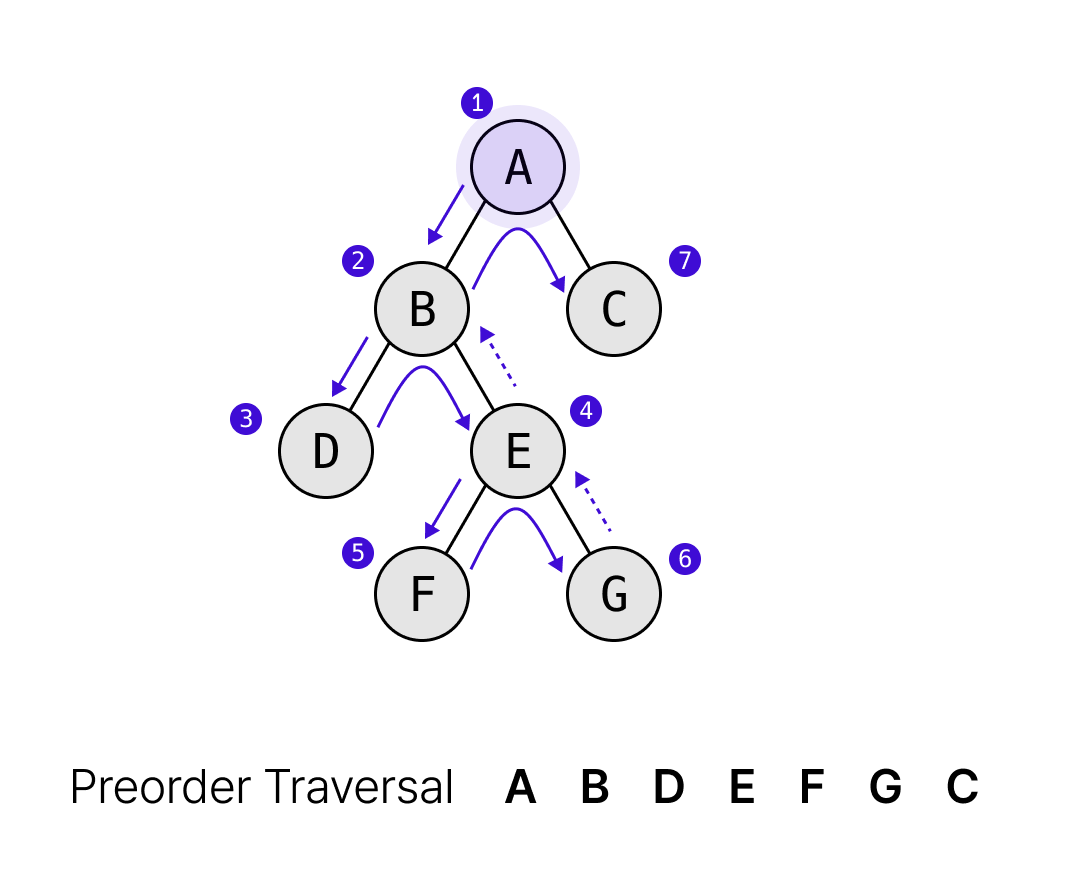
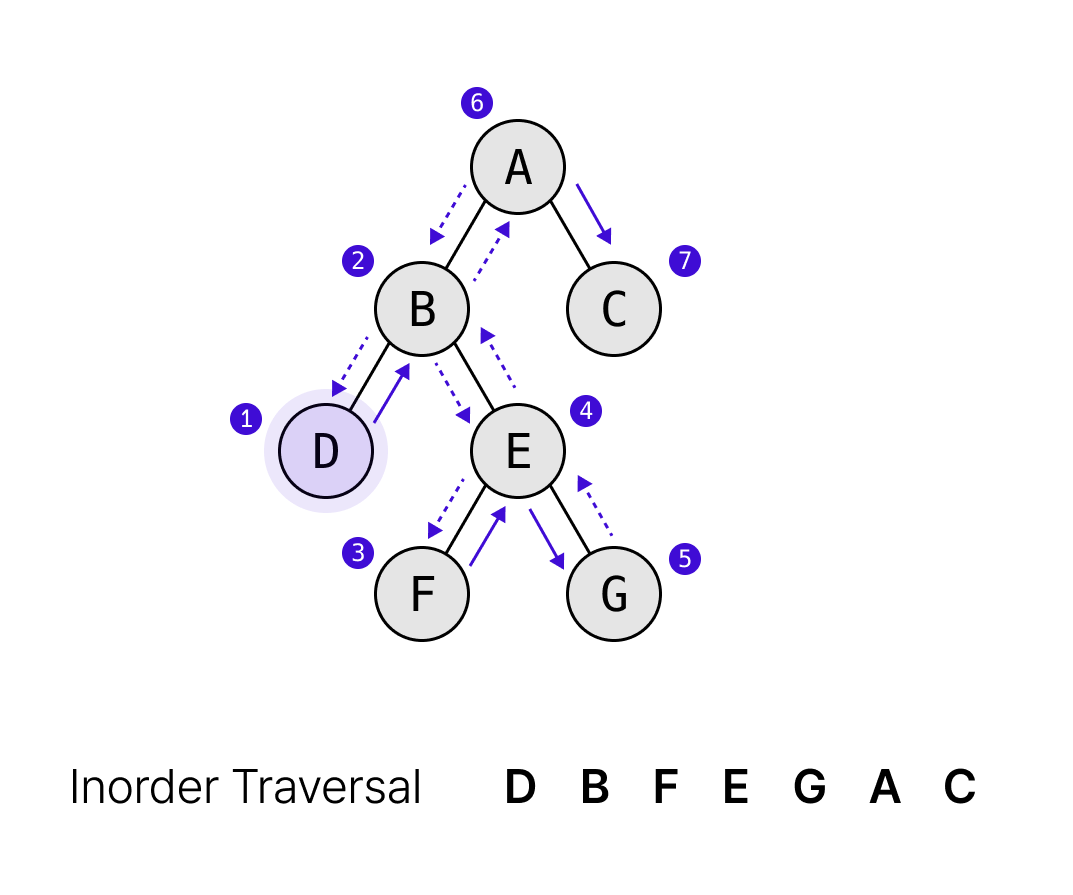
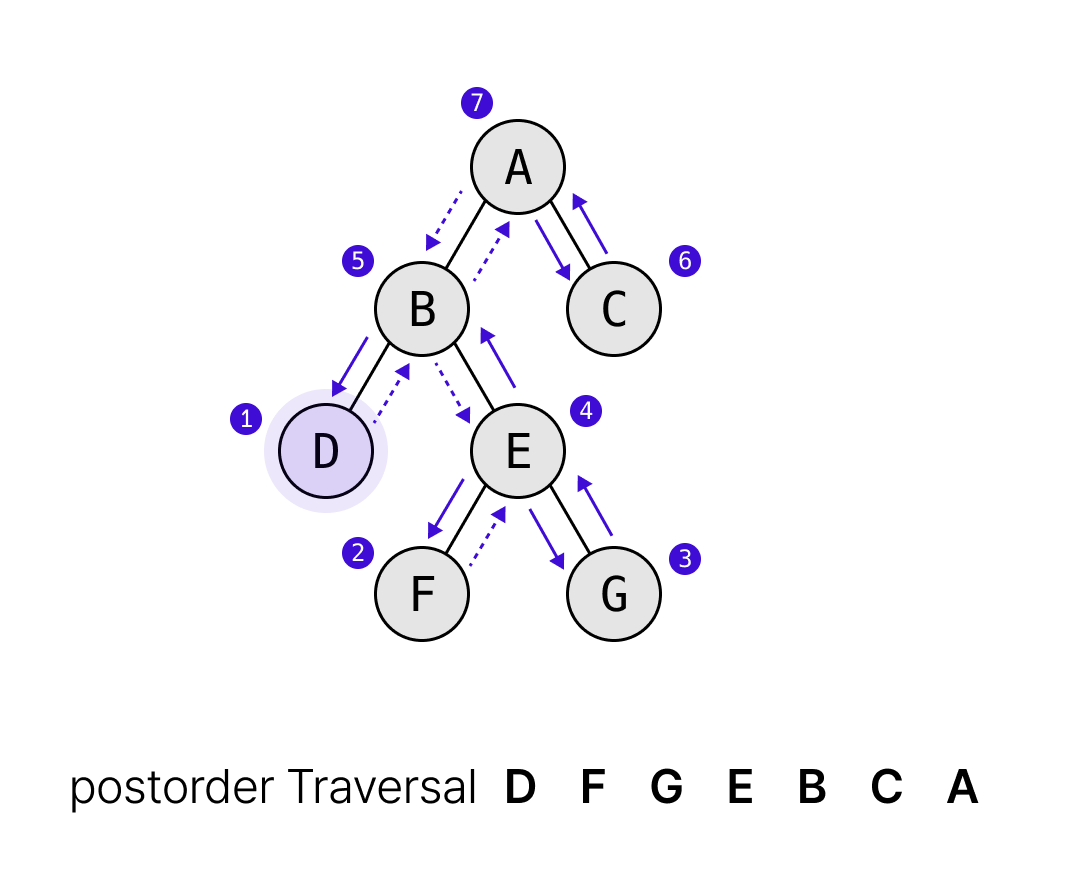
이진트리의 순회는 재귀를 통해 이루어진다.

#include <stdio.h>
#include <stdlib.h>
#include "BinaryTree2.h"

BTreeNode * MakeBTreeNode(void)
{
	BTreeNode * nd = (BTreeNode*)malloc(sizeof(BTreeNode));

	nd->left = NULL;
	nd->right = NULL;
	return nd;
}

BTData GetData(BTreeNode * bt)
{
	return bt->data;
}

void SetData(BTreeNode * bt, BTData data)
{
	bt->data = data;
}

BTreeNode * GetLeftSubTree(BTreeNode * bt)
{
	return bt->left;
}

BTreeNode * GetRightSubTree(BTreeNode * bt)
{
	return bt->right;
}

void MakeLeftSubTree(BTreeNode * main, BTreeNode * sub)
{
	if(main->left != NULL)
		free(main->left);

	main->left = sub;
}

void MakeRightSubTree(BTreeNode * main, BTreeNode * sub)
{
	if(main->right != NULL)
		free(main->right);

	main->right = sub;
}

// 전위 순회 함수
void PreorderTraverse(BTreeNode * bt, VisitFuncPtr action)
{
	if(bt == NULL)
		return;

	action(bt->data); // 전위 순회이므로 루트 노드 먼저 방문
	PreorderTraverse(bt->left, action);
	PreorderTraverse(bt->right, action);
}

// 중위 순회 함수
void InorderTraverse(BTreeNode * bt, VisitFuncPtr action)
{
	if(bt == NULL)
		return;

	InorderTraverse(bt->left, action); 
	action(bt->data); // 중위 순회이므로 루트 노드 중간에 방문
	InorderTraverse(bt->right, action);
}

// 후위 순회 함수
void PostorderTraverse(BTreeNode * bt, VisitFuncPtr action)
{
	if(bt == NULL)
		return;

	PostorderTraverse(bt->left, action);
	PostorderTraverse(bt->right, action);
	action(bt->data); // 후위 순회이므로 루트 노드 마지막에 방문
}

// 노드를 소멸 시키는 함수
void DeleteTree(BTreeNode * bt)
{
	if(bt == NULL)
		return;

	DeleteTree(bt->left);
	DeleteTree(bt->right);

	printf("del tree data: %d \n", bt->data);
	free(bt);
}

여기서 주목해야할 점은 순회 함수는 재귀적으로 이루어 지기 때문에 탈출 조건이 무조건 있어야한다. 

if(bt == NULL)
		return;

이 코드가 탈출 조건이다.

마지막으로 나오는 노드를 소멸 시키는 함수는 반드시 후위 순회로 이루어진다. 그 이유는 루트 노드가 마지막에 소멸되어야 하기 때문이다.

수식 트리(Expression Tree) 의 구현

수식 트리 : 이진 트리를 이용해서 수식을 표현해 놓은 것

수식 트리를 구성하는 방법은 “중위 표기법의 수식” ⇒ “후위 표기법의 수식” ⇒ “수식 트리” 와 같은 과정을 거친다.

여기서 중위 표기법을 후위 표기법으로 바꾸는 과정은 스택(무한 계산기 구현) 에서 진행한 바 있으므로 후위 표기법의 수식을 기반으로 수식 트리 구성해주기만 하면 된다.

  1. 피연산자를 만나면 무조건 스택으로 옮긴다.
  2. 연산자를 만나면 스택에서 두 개의 피연산자를 꺼내어 자식 노드로 연결한다.
  3. 자식 노드를 연결해서 만들어진 트리는 다시 스택으로 옮긴다.
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <ctype.h>
#include "ListBaseStack.h"
#include "BinaryTree2.h"

// 수식 트리를 만드는 함수
BTreeNode * MakeExpTree(char exp[])
{
	Stack stack; // stack 선언
	BTreeNode * pnode; // node 선언

	int expLen = strlen(exp); // 문자열의 길이
	int i;

	StackInit(&stack); // stack 초기화

	for(i=0; i<expLen; i++)
	{
		pnode = MakeBTreeNode(); // node 초기화

		if(isdigit(exp[i]))		// 피연산자라면
		{
			SetData(pnode, exp[i]-'0'); // node에 바로 값을 넣어줌
		}
		else					// 연산자라면
		{
			MakeRightSubTree(pnode, SPop(&stack)); // 스택에서 위에 들어있는 값을 pop 해주어 오른쪽 자식 노드에 넣어줌
			MakeLeftSubTree(pnode, SPop(&stack));  // 스택에서 아래에 들어있는 값을 pop 해주어 왼쪽 자식 노드에 넣어줌
			SetData(pnode, exp[i]); // 피연산자를 자식노드로 가지는 부모노드에 연산자를 넣어줌
		}

		SPush(&stack, pnode); // 스택에 해당 노드를 넣어줌
	}

	return SPop(&stack); 
}

// 수식 트리에 담겨있는 수식을 계산하는 함수
int EvaluateExpTree(BTreeNode * bt)
{
	int op1, op2;

	if(GetLeftSubTree(bt)==NULL && GetRightSubTree(bt)==NULL) // 단말 노드라면
		return GetData(bt); // 바로 값 반환해줌

	op1 = EvaluateExpTree(GetLeftSubTree(bt)); // 왼쪽 서브 트리 계산
	op2 = EvaluateExpTree(GetRightSubTree(bt)); // 오른쪽 서브 트리 계산

	switch(GetData(bt))
	{
	case '+':
		return op1+op2;
	case '-':
		return op1-op2;
	case '*':
		return op1*op2;
	case '/':
		return op1/op2;
	}

	return 0;
}

// 노드에 저장된 데이터를 출력하는 함수
void ShowNodeData(int data)
{
	if(0<=data && data<=9)
		printf("%d ", data); // 피연산자 출력
	else
		printf("%c ", data); // 연산자 출력
}

// 전위 표기법으로 수식 출력
void ShowPrefixTypeExp(BTreeNode * bt)
{
	PreorderTraverse(bt, ShowNodeData);
}

// 중위 표기법으로 수식 출력
void ShowInfixTypeExp(BTreeNode * bt)
{
	InorderTraverse(bt, ShowNodeData);
} 

// 후위 표기법으로 수식 출력
void ShowPostfixTypeExp(BTreeNode * bt)
{
	PostorderTraverse(bt, ShowNodeData);
}

위의 코드는 수식 트리를 구현한 코드로 수식을 수식 트리로 바꾸어 주는 함수, 해당 수식 트리의 값을 반환해주는 함수, 수식 트리를 전위, 중위, 후위 표기법으로 출력하는 함수가 담겨져 있다.

profile
섭승이
초보개발자입니당
이전 포스트

승섭 7/22

다음 포스트

승섭 7/24

post-custom-banner

1개의 댓글

comment-user-thumbnail
happy
2023년 7월 23일

잘 읽었습니다. 좋은 정보 감사드립니다.

답글 달기