Chapter 09. 우선순위 큐(Priority Queue)와 힙(Heap)

우선순위 큐의 이해

“큐”는 연산의 결과로 먼저 들어간 데이터가 먼저 나오는 FIFO 형식이다.

“우선순위 큐” 는 들어간 순서에 상관없이 우선순위가 높은 데이터가 먼저 나온다.

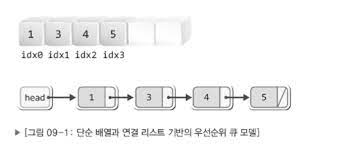
우선순위 큐의 구현 방법은 크게 3가지로 구분 된다.

• 배열을 기반으로 구현하는 방법
• 연결 리스트를 기반으로 구현하는 방법
• 힙(heap)을 이용하는 방법

우선 배열을 기반으로 구현하는 방법의 경우에는 2가지 단점이 있다.

1. 데이터를 삽입 및 삭제하는 과정에서 데이터를 한 칸씩 뒤로 밀거나 한 칸씩 앞으로 당기는 연산을 수반해야 한다.
2. 삽입의 위치를 찾기 위해서 배열에 저장된 모든 데이터와 우선순위의 비교를 진행해야 할 수도 있다.

연결리스트를 기반으로 구현하는 경우에도 단점이 있다.

1. 삽입의 위치를 찾기 위해서 첫 번째 노드에서부터 시작해서 마지막 노드에 저장된 데이터와 우선순위의 비교를 진행해야 할 수도 있다.

따라서 단순 배열도 연결 리스트도 아닌 “힙”이라는 자료구조를 이용해서 우선순위 큐를 구현하는 것이 좋다.

“힙”은 이진 트리이되 완전 이진 트리이다. 그리고 모든 노드에 저장된 값은 자식 노드에 저장된 값보다 크거나 같아야 한다. 즉 루트 노드에 저장된 값이 가장 커야 한다.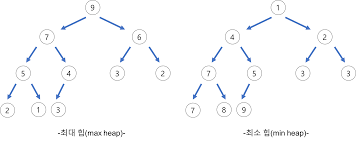

최대 힙 : 루트 노드로 올라갈수록 저장된 값이 커지는 완전 이진 트리

최소 힙 : 루트 노드로 올라갈수록 저장된 값이 작아지는 완전 이진 트리

---

힙의 구현과 우선순위 큐의 완성

힙을 구현하기 위해서는 데이터의 저장과 삭제의 방법을 먼저 알아야 한다.

먼저 데이터의 저장 과정을 ‘최소 힙’을 기준으로 설명하고자 한다.

우선 데이터를 저장할 때 “새로운 데이터는 우선순위가 가장 낮다는 가정하에서 마지막 위치에 저장하고 부모 노드의 우선순위를 비교해서 위치가 바뀌어야 한다면 바꿔주며 바뀐 다음에서 계속해서 부모 노드와 비교한다.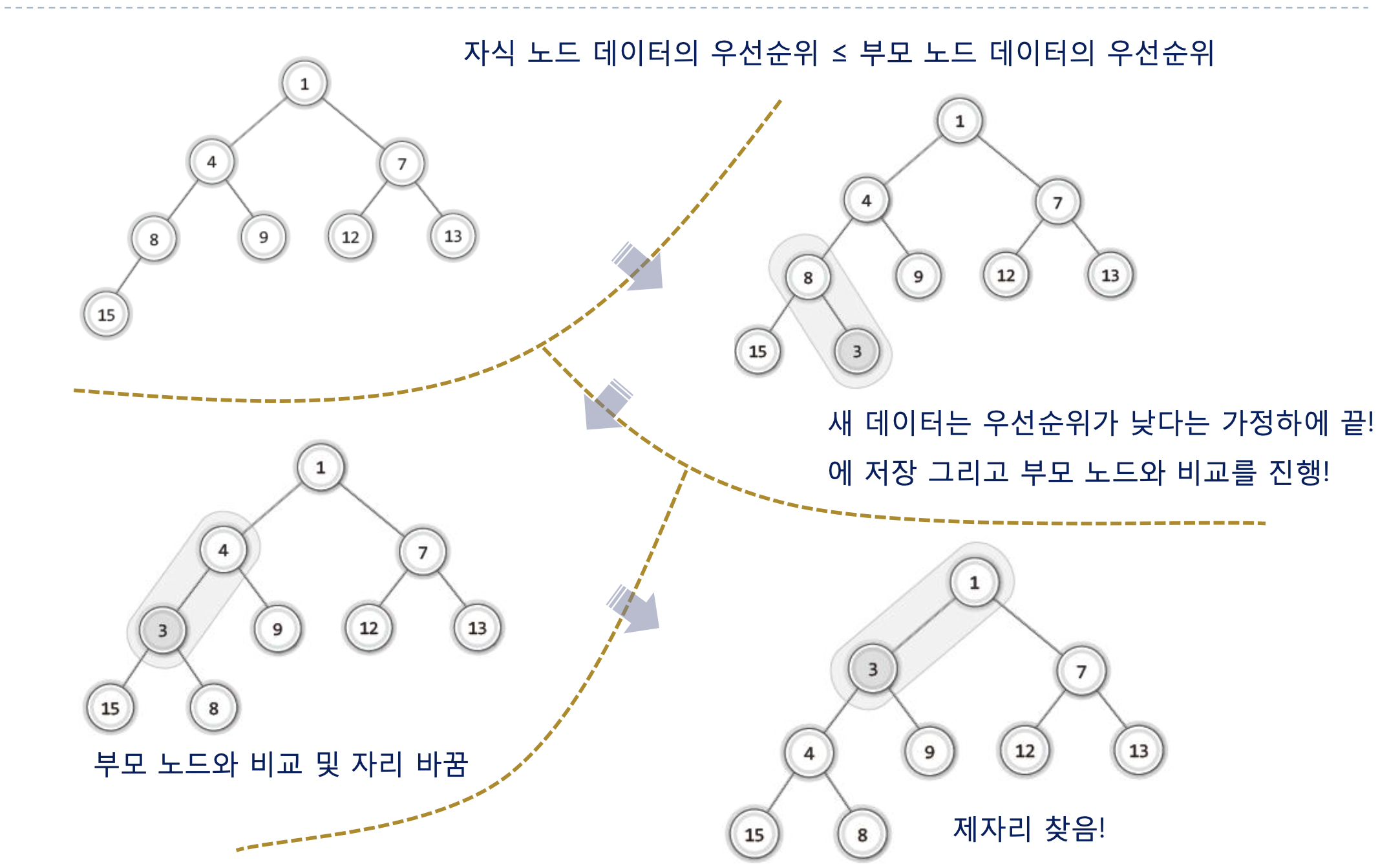

데이터를 삭제할 때는 루트 노드를 삭제한 다음에 이 부분을 어떻게 채울 지에 대한 고민이 필요하다.

“마지막 노드를 루트 노드의 자리로 옮긴 다음에, 자식 노드와의 비교를 통해서 제자리를 찾아가게 한다.” 라는 방식으로 힙에서 데이터 삭제를 할 수 있다.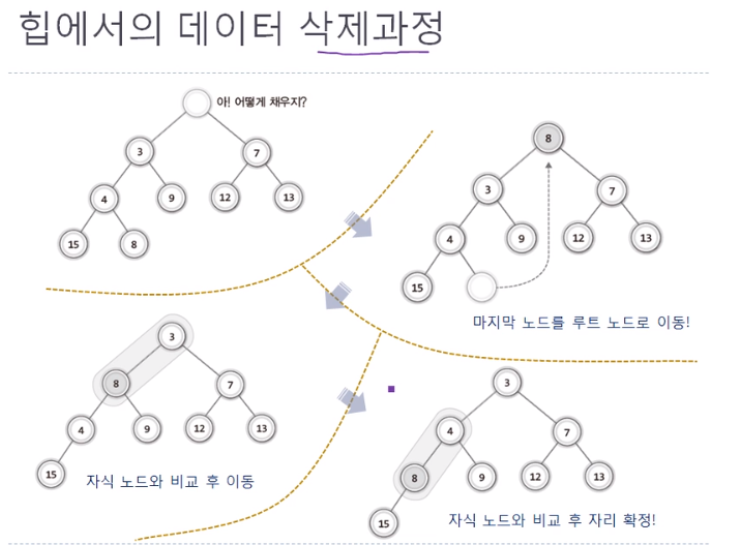

우선순위 큐의 구현에 있어서 단순 배열이나 연결 리스트보다 힙이 더 적합한 이유로는 시간 복잡도를 통해 알 수 있다.

• 배열 기반 데이터 저장의 시간 복잡도 ⇒ O(n)
• 배열 기반 데이터 삭제의 시간 복잡도 ⇒ O(1)
• 연결 리스트 기반 데이터 저장의 시간 복잡도 ⇒ O(n)
• 연결 리스트 기반 데이터 삭제의 시간 복잡도 ⇒ O(1)
• 힙 기반 데이터 저장의 시간 복잡도 ⇒ O(log2n)
• 힙 기반 데이터 삭제의 시간 복잡도 ⇒ O(log2n)

알고리즘 성능에 있어서 O(n) 과 O(log2n)의 차이는 굉장히 크기 때문에 우선순위 큐의 구현에 있어서 힙이 어울린다고 객관적으로 판단이 가능하다.

“힙”을 구현할 때는 배열을 기반으로 구현해야 하는데 그 이유는 다음과 같다.

“연결 리스트를 기반으로 힙을 구현하면, 새로운 노드를 힙의 ‘마지막 위치’에 추가하는 것이 쉽지 않다.”

힙을 구현할 때 알아야 하는 지식

• 힙은 완전 이진 트리이다.
• 힙의 구현은 배열을 기반으로 하며 인덱스가 0인 요소는 비워둔다.
• 따라서 힙에 저장된 노드의 개수와 마지막 노드의 고유번호는 일치한다.
• 노드의 고유번호가 노드가 저장되는 배열의 인덱스 값이 된다.
• 우선순위를 나타내는 정수 값이 작을수록 높은 우선순위를 나타낸다고 가정한다.

#include "UsefulHeap.h"

// 힙의 초기화
void HeapInit(Heap * ph, PriorityComp pc)
{
	ph->numOfData = 0;
	ph->comp = pc; // 우선순위 비교해주는 함수 포인터
}

// 힙이 비었는지 확인
int HIsEmpty(Heap * ph)
{
	if(ph->numOfData == 0)
		return TRUE;
	else
		return FALSE;
}

// 부모 노드의 인덱스 값 반환
int GetParentIDX(int idx) 
{ 
	return idx/2; 
}

// 왼쪽 자식 노드의 인덱스 값 반환
int GetLChildIDX(int idx) 
{ 
	return idx*2; 
}

// 오른쪽 자식 노드의 인덱스 값 반환
int GetRChildIDX(int idx) 
{ 
	return GetLChildIDX(idx)+1; 
}

// 두 개의 자식 노드 중 높은 우선순위의 자식 노드 인덱스 값 반환
int GetHiPriChildIDX(Heap * ph, int idx)
{
	// 자식 노드가 존재하지 않는다면
	if(GetLChildIDX(idx) > ph->numOfData)
		return 0;
	// 자식 노드가 하나만 존재한다면
	else if(GetLChildIDX(idx) == ph->numOfData)
		return GetLChildIDX(idx); // 완전 이진 트리이므로 왼쪽에만 존재

	// 자식 노드가 둘 다 존재한다면
	else
	{
	//	if(ph->heapArr[GetLChildIDX(idx)].pr 
	//				> ph->heapArr[GetRChildIDX(idx)].pr)
		// 오른쪽 자식 노드의 우선순위가 높다면
		if(ph->comp(ph->heapArr[GetLChildIDX(idx)], 
					ph->heapArr[GetRChildIDX(idx)]) < 0)
			return GetRChildIDX(idx); // 오른쪽 자식 노드의 인덱스 값 반환
		// 왼쪽 자식 노드의 우선순위가 높다면
		else
			return GetLChildIDX(idx); // 왼쪽 자식 노드의 인데긋 값 반환
	}
}

// 힙에서 데이터 삽입
void HInsert(Heap * ph, HData data)
{
	int idx = ph->numOfData+1; // 새 노드가 저장될 인덱스 값을 idx에 저장
	
	// 새 노드가 저장될 위치가 루트 노드의 위치가 아니라면 while문 반복
	while(idx != 1)
	{
	//	if(pr < (ph->heapArr[GetParentIDX(idx)].pr))
		// 새 노드와 부모 노드의 우선순위 비교
		if(ph->comp(data, ph->heapArr[GetParentIDX(idx)]) > 0) // 새 노드의 우선순위 높다면
		{
			// 부모 노드를 한 레벨 내림, 실제로 내림
			ph->heapArr[idx] = ph->heapArr[GetParentIDX(idx)];
			// 새 노드를 한 레벨 올림, 실제로 올리지는 않고 인덱스 값만 갱신
			idx = GetParentIDX(idx);
		}
		// 새 노드의 우선순위가 높지 않다면
		else
		{
			break;
		}
	}
	
	ph->heapArr[idx] = data; // 새 노드를 배열에 저장
	ph->numOfData += 1;
}

// 힙에서 데이터 삭제
HData HDelete(Heap * ph)
{
	HData retData = ph->heapArr[1]; // 반환을 위해서 삭제할 데이터 저장
	HData lastElem = ph->heapArr[ph->numOfData]; // 힙의 마지막 노드 저장
 
  // 아래의 변수 parentIdx에는 마지막 노드의 저장될 위치정보가 담긴다.
	int parentIdx = 1; // 루트 노드가 위치해야 할 인덱스 값 저장
	int childIdx;
	
	// 루트 노드의 우선순위가 높은 자식 노드를 시작으로 반복문 시작
	while(childIdx = GetHiPriChildIDX(ph, parentIdx))
	{
	//	if(lastElem.pr <= ph->heapArr[childIdx].pr)
		if(ph->comp(lastElem, ph->heapArr[childIdx]) >= 0) // 마지막 노드와 우선순위 비교
			break; // 마지막 노드의 우선순위가 높다면 반복문 탈출
		
		// 마지막 노드보다 우선순위 높으니, 비교대상 노드의 위치를 한 레벨 올림
		ph->heapArr[parentIdx] = ph->heapArr[childIdx]; 
		parentIdx = childIdx; // 마지막 노드가 저장될 위치정보를 한 레벨 내림
	} // 반복문 탈출하면 parentIdx에는 마지막 노드의 위치 정보 저장됨

	ph->heapArr[parentIdx] = lastElem; // 마지막 노드 최종 저장
	ph->numOfData -= 1;
	return retData;
}

힙을 구현하였으니 우선순위 큐를 구현해야함. 먼저 우선순위 큐 자료구조의 ADT부터 정의한다.

• void PQueueInit(PQueue * ppq, PriorityComp pc);
  • 우선순위 큐의 초기화를 진행한다.
  • 우선순위 큐 생성 후 제일 먼저 호출되어야 하는 함수이다.
• int PQIsEmpty(PQueue * ppq);
  • 우선순위 큐가 빈 경우 TRUE(1)을, 그렇지 않은 경우 FALSE(0)을 반환한다.
• void PEnqueue(PQueue * ppq, PQData data);
  • 우선순위 큐에 데이터를 저장한다.
  • 매개변수 data로 전달된 값을 저장한다.
• PQData PDequeue(PQueue * ppq);