Chapter 10. 정렬 (Sorting) - 1
단순한 정렬 알고리즘
버블 정렬(Bubble Sort) : 이해와 구현
위의 그림은 버블 정렬이 이루어지는 과정을 설명한 그림이다.
#include <stdio.h>
void BubbleSort(int arr[], int n)
{
int i, j;
int temp;
for(i=0; i<n-1; i++)
{
for(j=0; j<(n-i)-1; j++)
{
if(arr[j] > arr[j+1])
{
// 데이터의 교환
temp = arr[j];
arr[j] = arr[j+1];
arr[j+1] = temp;
}
}
}
}
int main(void)
{
int arr[4] = {3, 2, 4, 1};
int i;
BubbleSort(arr, sizeof(arr)/sizeof(int));
for(i=0; i<4; i++)
printf("%d ", arr[i]);
printf("\n");
return 0;
}정렬 알고리즘의 성능 평가
- 비교의 횟수
- 이동의 횟수
실제로 시간 복잡도에 대한 빅-오를 결정하는 기준은 “비교의 횟수”이다. 하지만 “이동의 횟수” 까지 살펴 보면 동일한 빅-오의 복잡도를 갖는 알고리즘 간의 세밀한 비교가 가능하다.
버블 정렬의 비교 횟수는 이중 포문 안에 있는 if문의 실행 횟수를 기준으로 계산하며 버블정렬의 비교연산에 대한 빅-오는 최악의 경우와 최선의 경우 구분 없이 O(n^2)이다.
또한 이동의 횟수는 최선의 경우 이미 정렬되어 있는 상태로 데이터의 이동이 한번도 일어나지 않지만, 최악의 경우 O(n^2)와 같다.
선택 정렬(Selection Sort) : 이해와 구현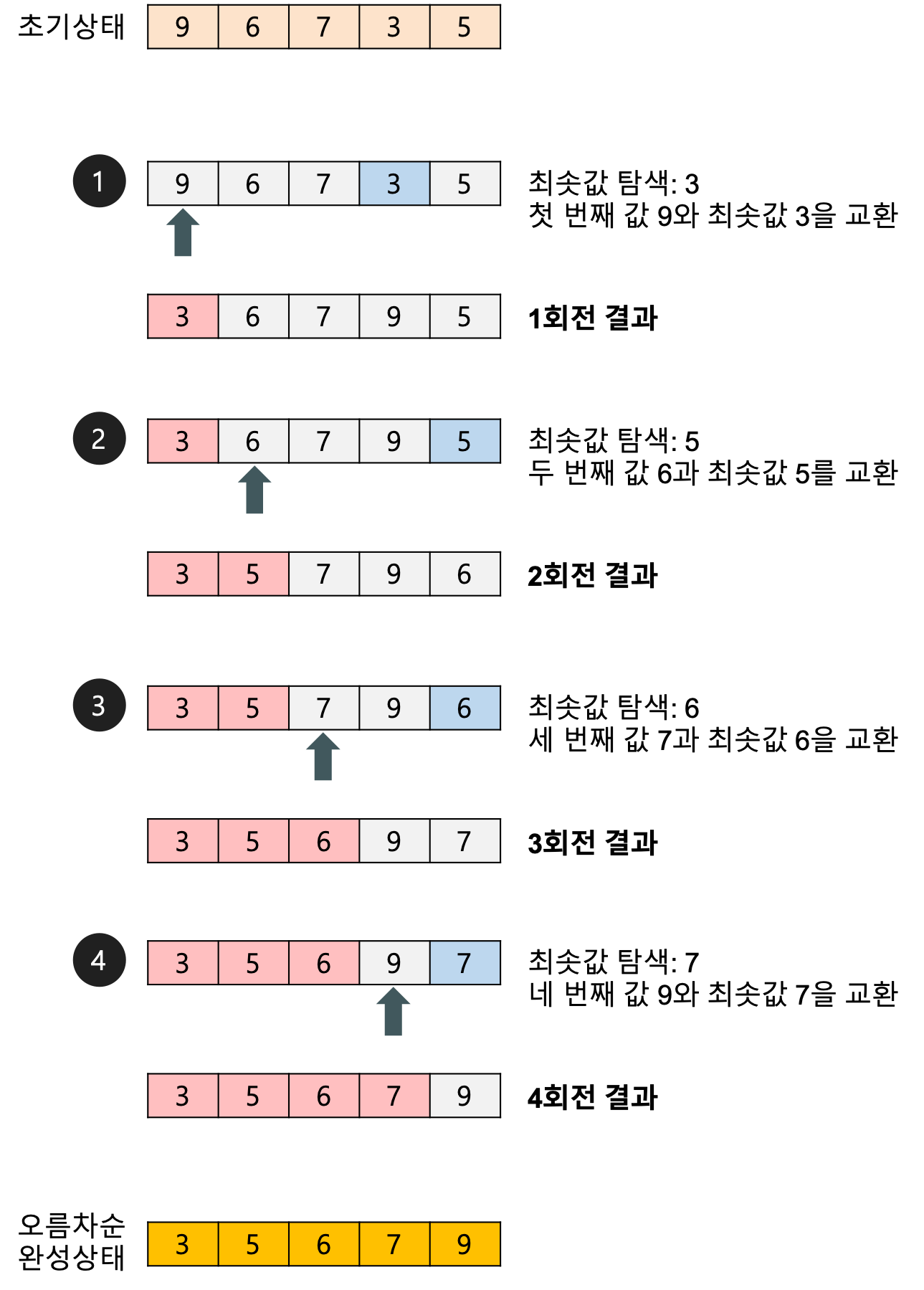
선택 정렬은 정렬 순서에 맞게 하나씩 선택해서 옮기는 옮기면서 정렬이 되게 하는 알고리즘이다.
#include <stdio.h>
void SelSort(int arr[], int n)
{
int i, j;
int maxIdx;
int temp;
for(i=0; i<n-1; i++)
{
maxIdx = i;
for(j=i+1; j<n; j++) // 최솟값 탐색
{
if(arr[j] < arr[maxIdx])
maxIdx = j;
}
// 교환
temp = arr[i];
arr[i] = arr[maxIdx];
arr[maxIdx] = temp;
}
}
int main(void)
{
int arr[4] = {3, 4, 2, 1};
int i;
SelSort(arr, sizeof(arr)/sizeof(int));
for(i=0; i<4; i++)
printf("%d ", arr[i]);
printf("\n");
return 0;
}선택 정렬의 코드만 봐도 버블 정렬과 성능상 큰 차이가 없음을 알 수 있다. 이중포문 안의 if절의 횟수로 비교횟수가 정해지기 때문이다. 따라서 선택 정렬의 빅-오 역시 최악의 경우와 최선의 경우 구분 없이 O(n^2)와 같다.
하지만 이동횟수는 버블 정렬과 다르다. 교환을 하는 코드의 위치가 바깥쪽 for문에 위치해 있기 때문이다. 따라서 이동횟수의 빅-오는 최악, 최선의 경우 구분 없이 O(n)과 같다.
결국 최악의 경우를 놓고 보면 버블 정렬보다 선택 정렬에 좋은 성능을 기대할 수 있지만, 최선의 경우 버블 정렬이 훨신 좋기 때문에 이 둘의 우열을 가리는 것은 무의미하다.
삽입 정렬(Insertion Sort) : 이해와 구현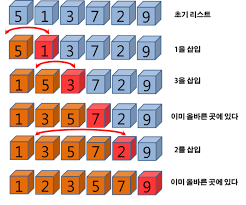
삽입 정렬은 위의 그림과 같이 정렬 대상을 두 부분으로 나눠서, 정렬 안 된 부분에 있는 데이터를 정렬 된 부분의 특정 위치에 삽입해 가면서 정렬을 진행하는 알고리즘이다.
#include <stdio.h>
void InserSort(int arr[], int n)
{
int i, j;
int insData;
for(i=1; i<n; i++)
{
insData = arr[i]; // 정렬 대상을 insData에 저장
for(j=i-1; j>=0 ; j--)
{
if(arr[j] > insData)
arr[j+1] = arr[j]; // 비교 대상 한 칸 뒤로 밀기
else
break; // 삽입위치 찾았으니 탈출
}
arr[j+1] = insData; // 찾은 위치에 정렬 대상 삽입
}
}
int main(void)
{
int arr[5] = {5, 3, 2, 4, 1};
int i;
InserSort(arr, sizeof(arr)/sizeof(int));
for(i=0; i<5; i++)
printf("%d ", arr[i]);
printf("\n");
return 0;
}삽입 정렬은 정렬 대상의 대부분이 이미 정렬되어 있는 경우 매우 빠르게 동작한다. 하지만 삽입 정렬의 빅-오는 최악의 경우 2중포문 안의 if절의 횟수로 따져야 하기 때문에 O(n^2)이 된다.
현재 진행중인 프로젝트에서 search 하는 기능을 개발하고 있는데 막힌 부분과 어떤 방식으로 구현하였는지 메모해놓겠습니다.
// 입력값이 변경될 때마다 필터링 로직을 실행합니다.
const filteredPosts = NEW_POSTS.filter((post) =>
post.title.toLowerCase().includes(searchValue.toLowerCase())
);
{/* 필터링된 결과를 사용하여 NewPostList 컴포넌트에 전달합니다. */}
{searchValue === "" ? null : (
<>
{filteredPosts.length > 0 ? (
<>
<p className="text-t300 text-body4">
총 {filteredPosts.length}개의 게시물을 찾았습니다.
</p>
<hr className="border border-[#F5F5F5] mt-5" />
<NewPostList data={filteredPosts} />
</>
) : (
<p className="text-t300 text-body4">
검색 결과가 없습니다. 다른 검색어로 시도해 보세요.
</p>
)}
</>
)}위의 코드는 Search.tsx 페이지의 일부 코드로 아직 디비 테이블에 데이터가 들어가지 않아서 NewPostList라는 더미데이터를 만들고 해당 더미데이터의 제목에 입력값이 들어가면 해당 더미데이터의 정보를 보여주고 아니면 "검색 결과가 없다" 라고 페이지에 보여주는 구조이다.
이때 input에
<input
type="text"
id="default-search"
className="block w-full h-full text-t500 text-[32px] p-5 outline-none"
placeholder="검색어를 입력해주세요."
required
value={searchValue} // 입력값 상태를 입력칸에 반영합니다.
onChange={(e) => setSearchValue(e.target.value)} // 입력값이 변경될 때마다 상태를 업데이트합니다.
/>이 코드를 넣어주면 해당 주석에 따라서 기능을 수행하게 된다.
