승섭 8/1

균형 잡힌 이진 탐색 트리 : AVL 트리의 이해

이진 탐색 트리의 연산은 O(log2n)의 시간 복잡도를 가진다. 그런데 이러한 이진 탐색 트리는 균형이 맞지 않을 수록 O(n)에 가까운 시간 복잡도를 보인다.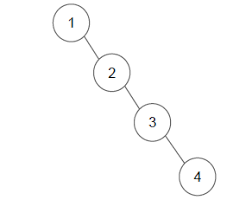

위의 그림과 같을때 2나 3을 루트 노드로 설정해주기만 하면 노드의 수의 가까운 높이를 형성한 트리의 성능을 올릴 수 있다.

AVL트리는 노드가 추가될 때, 삭제될 때 트리의 균형상태를 파악해서 스스로 그 구조를 변경하여 균형을 잡는 멋진 트리이다.

AVL트리에서는 균형의 정도를 표현하기 위해서 ‘균형 인수’ 라는 것을 사용하는데 이 균형인수는 다음과 같이 계산된다.

균형 인수 = 왼쪽 서브 트리의 높이 - 오른쪽 서브 트리의 높이

따라서 AVL 트리는 균형 인수의 절댓값이 2이상인 경우에 균형을 잡기 위한 트리의 재조정을 진행한다.

리밸런싱이 필요한 첫 번째 상태와 LL회전

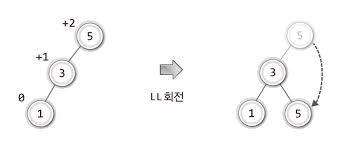
위의 그림에서 왼편을 보면 루트 노드의 균형 인수가 +2 이다. 이러한 상태를 ‘LL상태’라 하며, 이 상태에서 발생한 불균형의 해소를 위해 등장한 리밸런싱 방법을 가리켜 ‘LL회전’이라 한다.

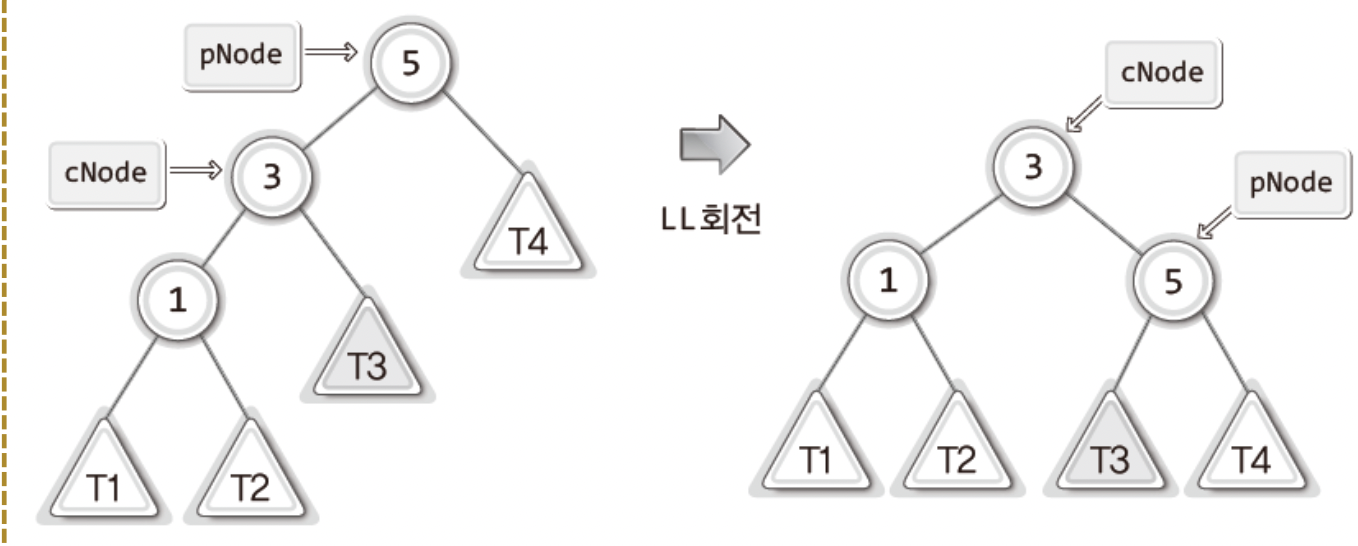
위의 그림처럼 LL회전을 진행하며 이를 코드로 나타내려면 다음 두 문장을 순서대로 실행해야 한다.

ChangeLeftSubTree(pNode, GetRightSubTree(cNode);
ChangeLeftSubTree(cNode, pNode);

리밸런싱이 필요한 두 번째 상태와 RR회전

RR회전과 LL회전의 유일한 차이점은 “방향”이라고 보는데

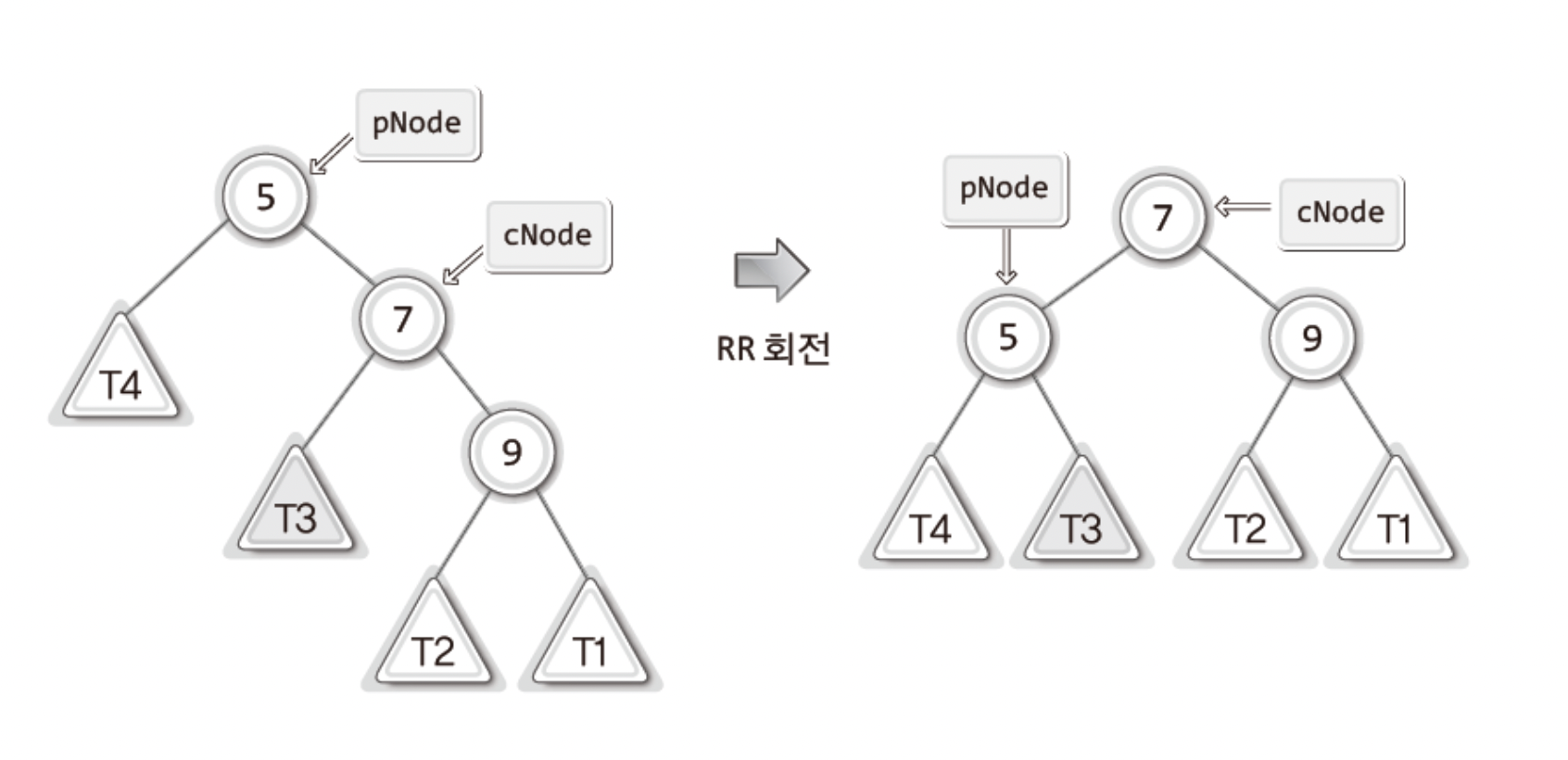
위의 그림을 통해 RR회전이 이루어지면 이를 코드로 나타내면

ChangeRightSubTree(pNode, GetLeftSubTree(cNode));
ChangeLeftSubTree(cNode, pNode);

리밸런싱이 필요한 세 번째 상태와 LR회전

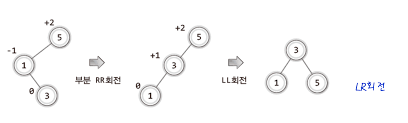
위의 그림에서 제일 왼쪽에 있는 상황을 LL상태라고 하며 부분 RR회전을 해준 뒤 LL회전을 해줌으로서 해결을 할 수 있고 이를 LR회전이라고 한다.

즉 1,3의 노드끼리 RR회전을 해주고 그 다음 LL회전을 해줌으로서 LR회전을 구현할 수 있다.

리밸런싱이 필요한 네 번째 상태와 RL회전

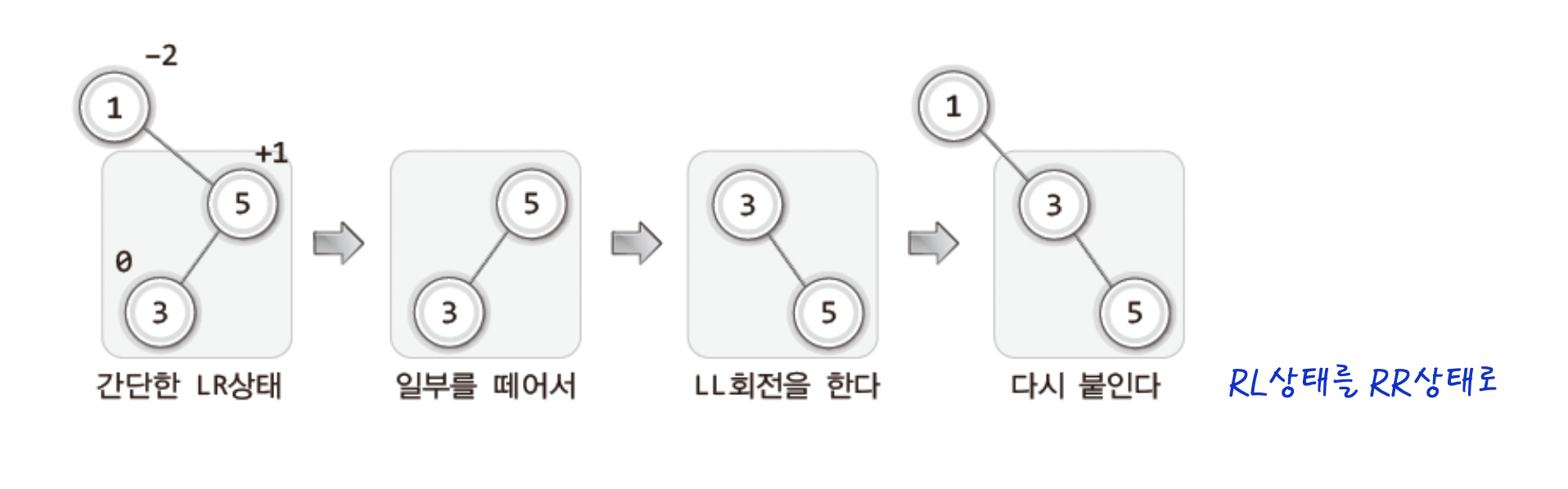
위의 그림을 통해 이해할 수 있다, LR회전과 회전하는 방향만 다를 뿐이다.

---

균형 잡인 이진 탐색 트리 : AVL 트리의 구현

#include <stdio.h>
#include "BinaryTree3.h"

// LL 회전을 담당하는 함수
BTreeNode * RotateLL(BTreeNode * bst)
{
	BTreeNode * pNode; // parent node
	BTreeNode * cNode; // child node

	// pNodedhk cNode가 LL회전을 위해 적절한 위치를 가리키게 한다.
	pNode = bst;
	cNode = GetLeftSubTree(pNode);

	// 실제 LL회전을 담당하는 두 개의 문장
	ChangeLeftSubTree(pNode, GetRightSubTree(cNode));
	ChangeRightSubTree(cNode, pNode);
	
	// LL회전을 인해서 변경된 루트 노드의 주소 값 반환
	return cNode;
}

// RR 회전을 담당하는 함수
BTreeNode * RotateRR(BTreeNode * bst)
{
	BTreeNode * pNode; // parent node
	BTreeNode * cNode; // child node

	// pNode와 cNode가 RR회전을 위해 적절한 위치를 가리키게 한다.
	pNode = bst;
	cNode = GetRightSubTree(pNode);

	// 실제 RR회전을 담당하는 두 개의 문장
	ChangeRightSubTree(pNode, GetLeftSubTree(cNode));
	ChangeLeftSubTree(cNode, pNode);
	
	// RR회전으로 인해서 변경된 루트 노드의 주소 값 반환
	return cNode;
}

// RL 회전을 담당하는 함수
BTreeNode * RotateRL(BTreeNode * bst)
{
	BTreeNode * pNode; // parent node
	BTreeNode * cNode; // child node

	// pNode와 cNode가 RL회전을 위해 적절한 위치를 가리키게 한다.
	pNode = bst;
	cNode = GetRightSubTree(pNode);

	ChangeRightSubTree(pNode, RotateLL(cNode));   // 부분적 LL회전
	return RotateRR(pNode);     // RR 회전
}

// LR 회전을 담당하는 함수
BTreeNode * RotateLR(BTreeNode * bst)
{
	BTreeNode * pNode; // parent node
	BTreeNode * cNode; // child node

	// pNode와 cNode가 LR회전을 위해 적절한 위치를 가리키게 한다.
	pNode = bst;
	cNode = GetLeftSubTree(pNode);
	
	ChangeLeftSubTree(pNode, RotateRR(cNode));   // 부분적 RR회전
	return RotateLL(pNode);     // LL 회전
}

// 트리의 높이를 계산하여 반환
int GetHeight(BTreeNode * bst) 
{
	int leftH;		// left height
	int rightH;		// right height

	if(bst == NULL)
		return 0;

	// 왼쪽 서브 트리 높이 계산
	leftH = GetHeight(GetLeftSubTree(bst));

	// 오른쪽 서브 트리 높이 계산
	rightH = GetHeight(GetRightSubTree(bst));

	// 큰 값의 높이를 반환
	if(leftH > rightH)
		return leftH + 1;
	else
		return rightH + 1;
}

// 두 서브 트리의 "높이의 차"를 반환
int GetHeightDiff(BTreeNode * bst)
{
	int lsh;    // left sub tree height
	int rsh;    // right sub tree height

	if(bst == NULL)
		return 0;

	lsh = GetHeight(GetLeftSubTree(bst));
	rsh = GetHeight(GetRightSubTree(bst));

	return lsh - rsh;
}

// 위에서 정의한 함수들의 사용순서 및 사용시기를 모두 담은 리밸런싱 함수
BTreeNode * Rebalance(BTreeNode ** pRoot)
{
	int hDiff = GetHeightDiff(*pRoot); // 균형 인수 계산

	// 균형 인수가 +2 이상이면 LL상태 또는 LR상태이다
	if(hDiff > 1)     // 왼쪽 서브 트리 방향으로 높이가 2 이상 크다면
	{
		if(GetHeightDiff(GetLeftSubTree(*pRoot)) > 0) // LL상태라면,
			*pRoot = RotateLL(*pRoot); // LL회전을 진행한다.
		else // LR상태라면,
			*pRoot = RotateLR(*pRoot); // LR회전을 진행한다.
	}
	
	// 균형 인수가 -2 이상이면 RR상태 또는 RL상태이다
	if(hDiff < -1)     // 오른쪽 서브 트리 방향으로 높이가 2 이상 크다면
	{
		if(GetHeightDiff(GetRightSubTree(*pRoot)) < 0) // RR상태라면,
			*pRoot = RotateRR(*pRoot); // RR회전을 진행한다.
		else // RL상태라면,
			*pRoot = RotateRL(*pRoot); // RL회전을 진행한다.
	}
	
	return *pRoot;
}