승섭 8/2

섭승이·2023년 8월 2일

개발일기 자료구조

자료구조

목록 보기

12/12

Chapter 13. 테이블(Table)과 해쉬(Hash)

빠른 탐색을 보이는 해쉬 테이블(map)

테이블(Table) 자료구조의 이해

테이블 자료구조의 탐색 연산은 O(1)의 시간 복잡도를 보인다.

“저장되는 데이터는 키(key)와 값(value)의 하나의 쌍을 이룬다.”
“키(key)는 존재하지 않는 값은 저장할 수 없다. 그리고 모든 키는 중복되지 않는다.”

위의 두개의 조건은 테이블의 기본 조건에 해당한다.

배열을 기반으로 하는 테이블

#include <stdio.h>

typedef struct _empInfo
{
	int empNum;    // 직원의 고유번호 : key
	int age;     // 직원의 나이 : value
}EmpInfo;

int main(void)
{
	EmpInfo empInfoArr[1000]; // 직원들의 정보를 저장하기 위해 선언된 배열
	EmpInfo ei;
	int eNum;

	printf("사번과 나이 입력: ");
	scanf("%d %d", &(ei.empNum), &(ei.age));
	empInfoArr[ei.empNum] = ei;    // 단번에 저장!

	printf("확인하고픈 직원의 사번 입력: ");
	scanf("%d", &eNum);

	ei = empInfoArr[eNum];    // 단번에 탐색!
	printf("사번 %d, 나이 %d \n", ei.empNum, ei.age);
	return 0;
}

위의 코드를 통해 “직원의 고유번호를 인덱스 값으로 하여, 그 위치에 데이터를 저장한다” 라는 사실을 알 수 있다.

테이블에 의미를 부여하는 해쉬 함수와 충돌문제

예제에서 보인 테이블과 관련하여 지적한 문제점 두 가지를 정리하면 다음과 같다.

직원 고유번호의 범위가 배열의 인덱스 값으로 사용하기에 적당하지 않다.
직원 고유번호의 범위를 수용할 수 있는 매우 큰 배열이 필요하다.

이 두 가지 문제를 동시에 해결해주는 것이 바로 “해쉬 함수”이다.

int GetHashValue(int empNum)
{
	return empNum % 100;
}

다음과 같은 함수를 해쉬함수라고 부르며 길이가 100인 배열을 선언했다고 가정할때 8자리의 수로 이루어진 직원의 고유번호를 마지막 2자리로 판단하도록 만들어 주는 것이다.

좋은 해쉬 함수란 “충돌”이 발생할 확률이 낮다는 것을 의미한다. 따라서 좋은 해쉬 함수는 키의 일부분을 참조하여 해쉬 값을 만들지 않고, 키 전체를 참조하여 해쉬 값을 만들어 낸다.

충돌(Collision) 문제의 해결책

선형 조사법(Linear Probing)과 이차 조사법(Quadratic Probing)

선형 조사법 : 충돌이 발생했을 때 그 옆자리가 비었는지 살펴보고, 비었을 경우 그 자리에 대신 저장하는 것
이차 조사법 : 선형 조사법의 단점을 보완하는 방법으로 보다 좀 멀리서 빈 공간을 찾는 것

선형 조사법은 충돌의 횟수가 증가함에 따라서 “클러스터 현상”, 쉬운 표현으로 특정 영역에 데이터가 집중적으로 몰리는 현상이 발생한다는 단점이 있다.

선형 조사법에서 키가 9인 데이터를 삭제할 때 테이블의 상태를 EMPTY가 아닌 DELETED로 바꾸는데 그 이유로 만약 키가 2인 데이터의 탐색을 진행하기 위해서는 %7의 해쉬 함수를 거치고, 그 결과로 얻은 2를 인덱스 값으로 하여 탐색을 진행하게 된다. 만약에 그 위치의 슬롯 상태가 EMPTY라면, 데이터가 존재하지 않는다고 판단하여 탐색을 종료하게 된다. 그 옆자리를 확인해야하기 때문에 DELETED 상태로 두는 것이다.

따라서 우리는 다음 두 가지 사실을 추가로 정리해야 한다.

선형, 이차 조사법과 같은 충돌의 해결책을 적용하기 위해서는 슬롯의 상태에 DELETED를 포함시켜야 한다.
선형, 이차 조사법을 적용하였다면, 탐색의 과정에서도 이를 근거로 충돌을 의심하는 탐색의 과정을 포함시켜야 한다.

이중 해쉬(Double Hash)

이차 조사법의 문제점 : 해쉬 값이 같으면, 충돌 발생시 빈 슬롯을 찾기 위해서 접근하는 위치가 늘 동일하다.

따라서 이중 해쉬 방식을 이용해 이를 해결할 수 있다.

1차 해쉬 함수 → 키를 근거로 저장위치를 결정하기 위한 것
2차 해쉬 함수 → 충돌 발생시 몇 칸 뒤를 살필지 결정하기 위한 것

1차 해쉬 함수 h1(k) = k % 15

2차 해쉬 함수 h2(k) = 1 + (k % 7)

먼저 1을 더한 이유는 2차 해쉬 값이 0이 되는 것을 막기 위해서이다.

7로 나누어 주는 이유는 15보다 작은 소수중 하나를 선택한 것이다.

15보다 작은 값으로 결정하는 이유 : 가급적 2차 해쉬 값이 1차 해쉬 값을 넘어서지 않게 하기 위함
소수로 결정하는 이유 : 소수를 선택했을 때 클러스터 현상의 발생 확률을 현저히 낮춘다는 통계 근거

이중 해쉬는 이상적인 충돌 해결책으로 알려져 있다.

체이닝(Chaining)

체이닝이랑 무슨 일이 있어도 자신의 자리에 저장을 한다는 의미로 충돌이 발생해도 자신의 자리에 들어가겠다는 의미이다.

따라서 2차원 배열 또는 연결리스트로 구현이 가능하다. 하지만 2차원 배열을 메모리 낭비가 심하고 충돌의 최대 횟수를 결정해야 하는 부담이 있기 때문에 보통 연결리스트로 구현을 많이 한다.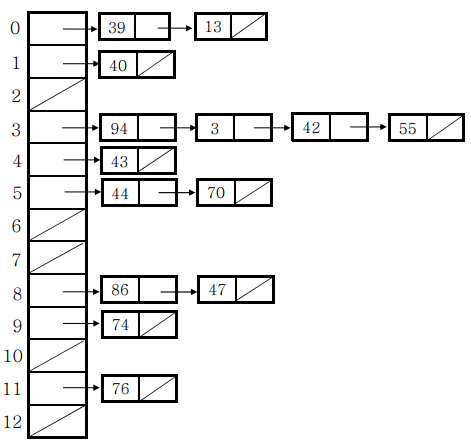

체이닝의 구현을 위한 두가지 방법

슬롯이 연결 리스트의 노드 역할을 하게 하는 방법
연결 리스트의 노드와 슬롯을 구분하는 방법

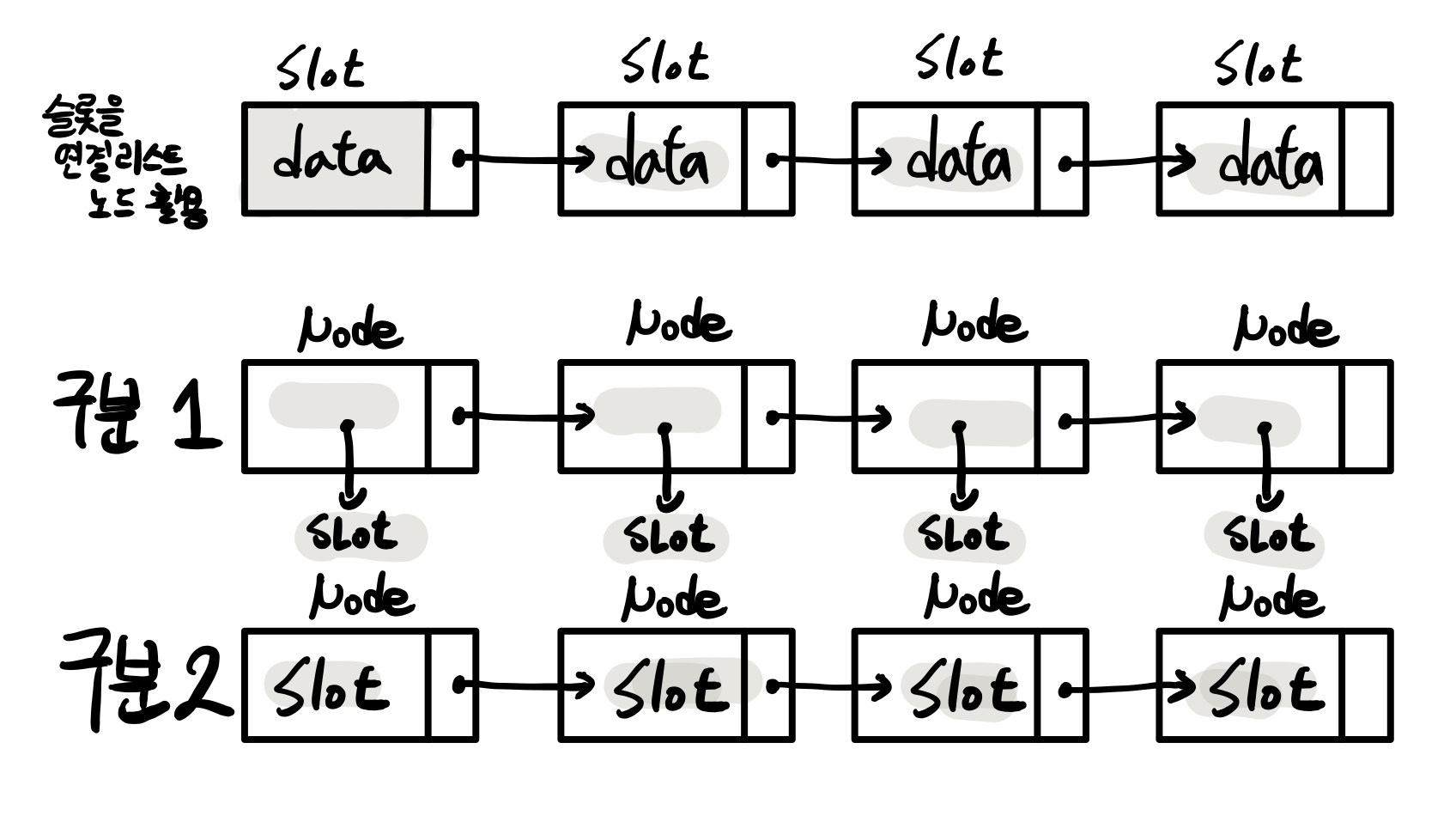
아래의 코드는 구분 2로 구현한 코드이다.

#include <stdio.h>
#include <stdlib.h>
#include "Table2.h"
#include "DLinkedList.h"

void TBLInit(Table * pt, HashFunc * f)
{
	int i;

	for(i=0; i<MAX_TBL; i++)
		ListInit(&(pt->tbl[i]));

	pt->hf = f;
}

void TBLInsert(Table * pt, Key k, Value v)
{
	int hv = pt->hf(k);
	Slot ns = {k, v};
	
	if(TBLSearch(pt, k) != NULL)       // 키가 중복되었다면
	{
		printf("≈∞ ¡ﬂ∫π ø¿∑˘ πﬂª˝ \n");
		return;
	}
	else
	{
		LInsert(&(pt->tbl[hv]), ns);
	}
}

Value TBLDelete(Table * pt, Key k)
{
	int hv = pt->hf(k);
	Slot cSlot;

	if(LFirst(&(pt->tbl[hv]), &cSlot))
	{
		if(cSlot.key == k)
		{
			LRemove(&(pt->tbl[hv]));
			return cSlot.val;
		}
		else
		{
			while(LNext(&(pt->tbl[hv]), &cSlot))
			{
				if(cSlot.key == k)
				{
					LRemove(&(pt->tbl[hv]));
					return cSlot.val;
				}
			}
		}
	}

	return NULL;
}

Value TBLSearch(Table * pt, Key k)
{
	int hv = pt->hf(k);
	Slot cSlot;

	if(LFirst(&(pt->tbl[hv]), &cSlot))
	{
		if(cSlot.key == k)
		{
			return cSlot.val;
		}
		else
		{
			while(LNext(&(pt->tbl[hv]), &cSlot))
			{
				if(cSlot.key == k)
					return cSlot.val;
			}
		}
	}

	return NULL;
}

섭승이

초보개발자입니당

이전 포스트