AI 부트캠프 27일차

학습목표

1. 머신러닝모델을 만들 때 학습과 테스트 데이터를 분리 해야 하는 이유
2. 다중선형회귀
3. 과적합/과소적합을 일반화 관점에서 설명
4. 편향/분산의 트레이트오프 개념을 이해하고 일반화 관점에서 설명

Warm-up : 질문

1. 회귀모델을 만들 때 기준모델을 어떻게 정의하나요? 이 과정이 왜 중요할까요?

예측 모델을 만들기 전에 간단하게 최소한의 성능을 나타내는 기준이 되는 모델

2. 회귀분석이 무엇인지 간단하게 설명해 보세요.

관찰된 연속형 변수들에 대해 두 변수 사이의 모형을 구한뒤 적합도를 측정해 내는 분석 방법

Warm-up : How to Calculate R Squared Using Regression Analysis

$\sum(\hat{y}-\bar{y}) = 0$, $\sum(y-\bar{y}) = 0$
-> 제곱하는이유

$\hat{y}$ : estimated value

• $R^2$은 1에 가까울 수록 좋은 fit
  $R^2=1$ : perfect fit (실젯값$y$과 예측값$\hat{y}$이 같음)
  $R^2=0$ : no relationship

Warm-up : Standard Error of the Estimate used in Regression Analysis (Mean Square Error)

($R^2$외에) goodness of fit을 예측하는 또 다른 방법

$n$ : number of observations

R Squared와 Standard Error of the Estimate

• R Squared (평균까지의 거리 비교)
  compare the distance between the actual values to the mean
  with the estimated values to the mean
• Standard Error of the Estimate
  compare estimated and actual values

MSE(Mean Squared Error)

정답에 가까울수록 작은값

Warm-up : Training and testing

*ealier data : train, later data : test
(반대로 하면 사전관찰편견(Look-ahead bias) 발생 할 수 있음)

1. Xtrain과 ytrain을 통해 Machine Learning을 하고 model을 만듦
2. Xtest을 model에 적용해서 y을 도출
3. y을 ytest와 비교(일치할수록 좋은 model)

훈련/테스트 데이터를 나누는 이유

test over the same data we trained on
-> train data와 test data 결과 일치
-> test data에 신뢰성 없음
-> 데이터를 train, test의 두 세트로 나눔

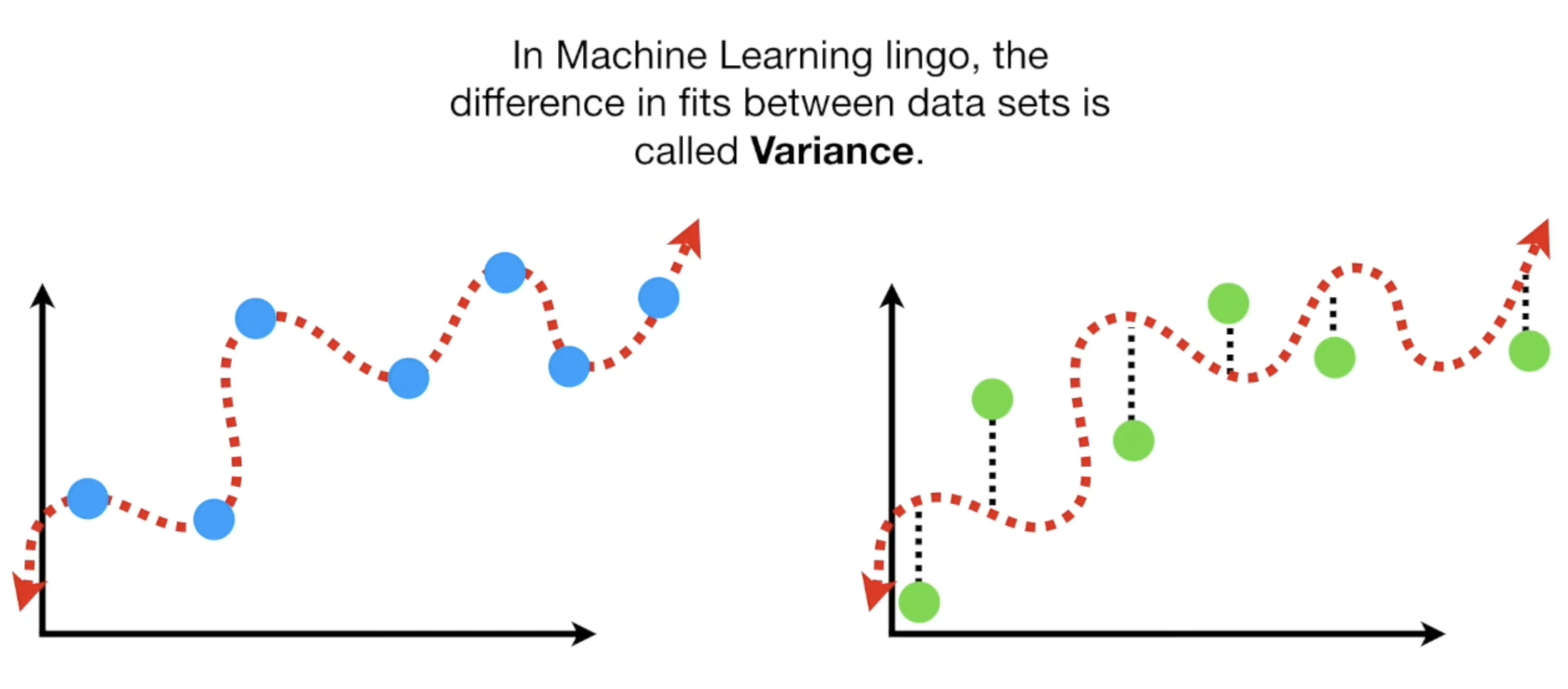
Warm-up : Machine Learning Fundamentals: Bias and Variance

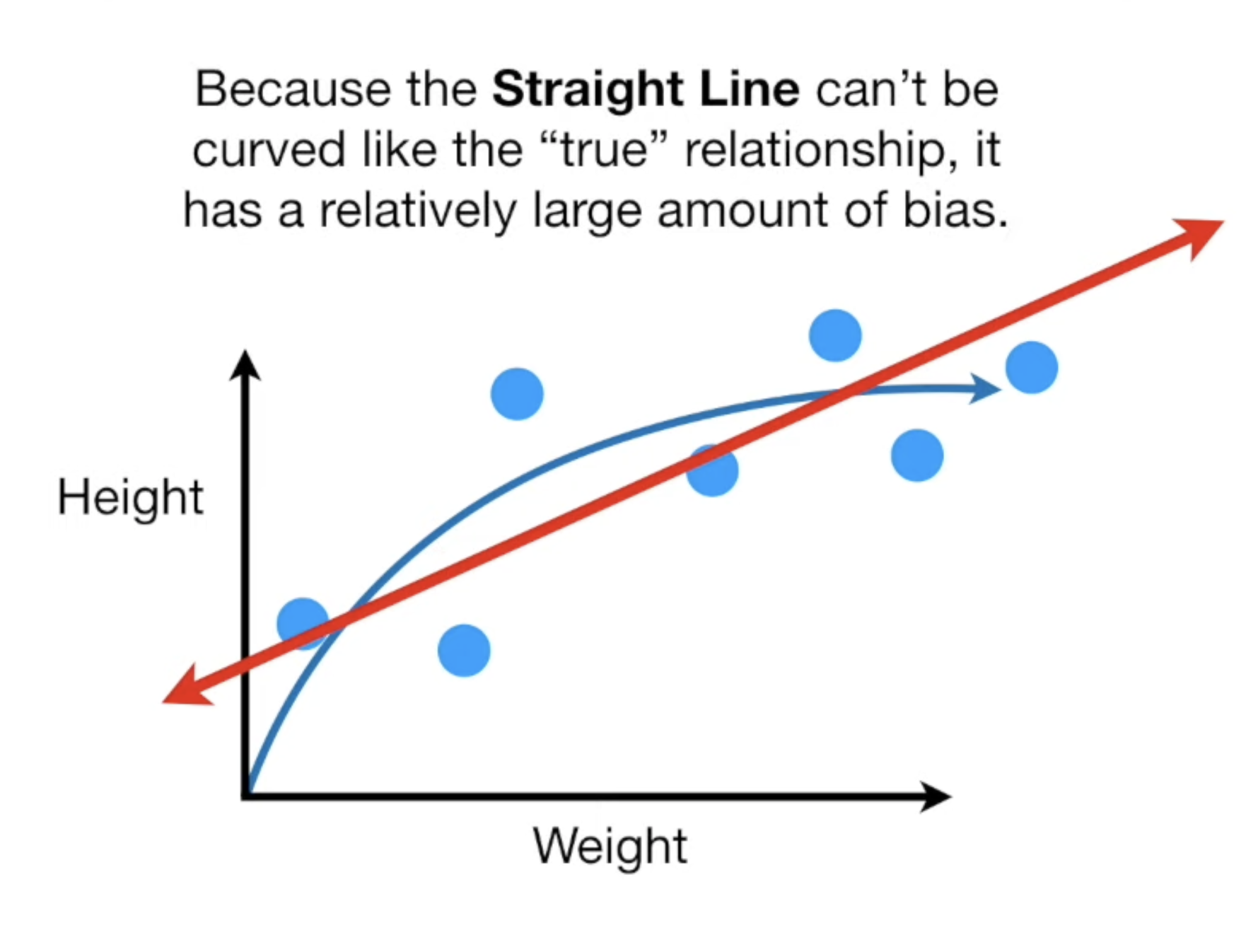
Suiggly Line vs Straight Line

• Suiggly Line
  low bias : flexible, can adapt to the curve in the relationship
  
  high variability : vastly different Sums of Squares for different datasets
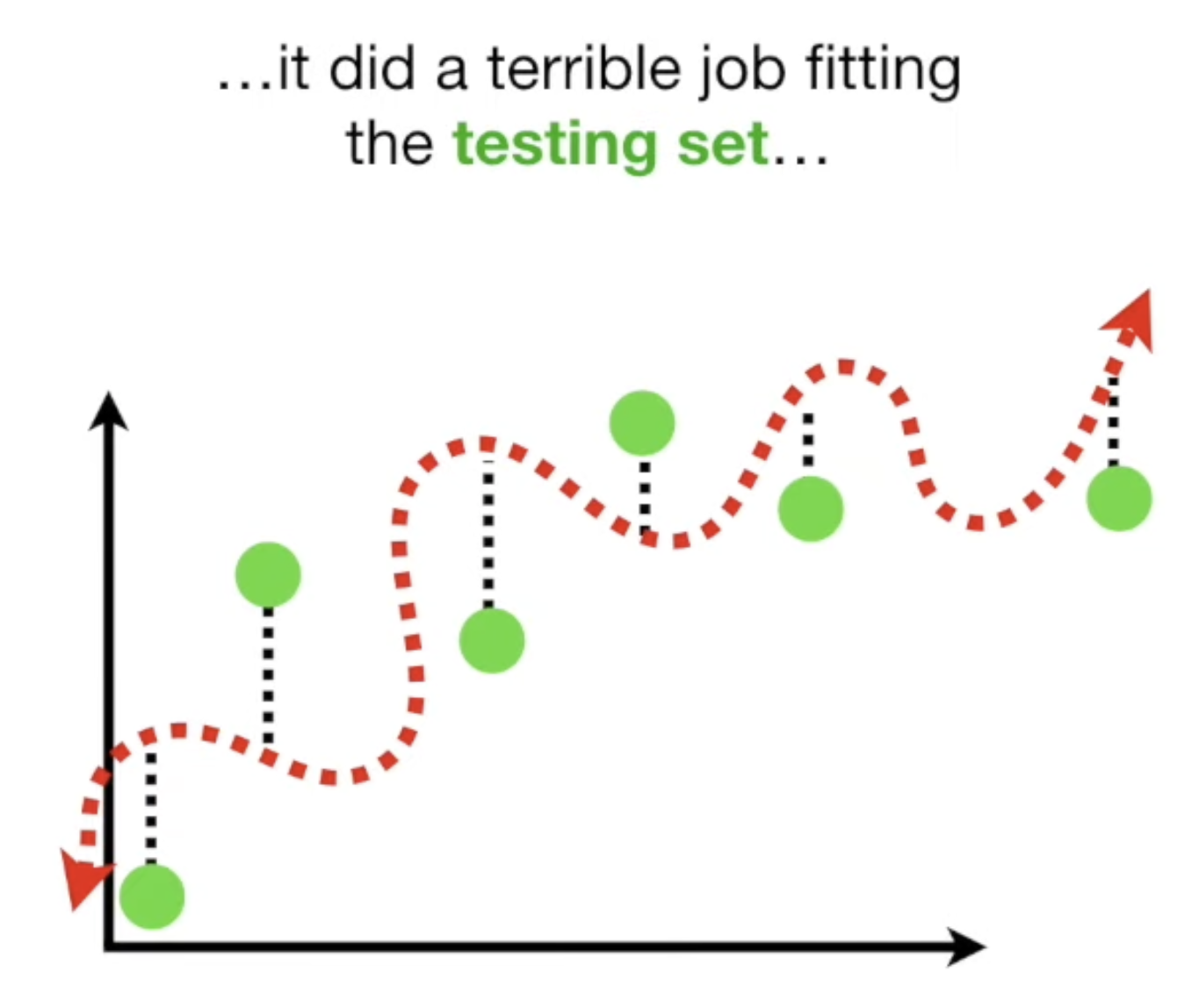
  (Because of high variability) hard to predict how well the Squiggly Line will perform with future data sets

overfit

fits the training set really well, but not the testing set

• Straight Line
  high bias : cannot capture the cure in the relationship
  low variance : Sums of Squares are similar for different datasets
  good predictions (and not great predictions)

• finding the sweet spot between simple and complicated models
  : regularization, boosting and bagging

Warm-up : Getting Started with Plotly in Python

학습/테스트 데이터 분리

훈련(train) 데이터를 잘 맞추는 모델이 아니라,
학습에 사용하지 않은 테스트(test) 데이터를 얼마나 잘 맞추는지 모델이 필요

학습에 사용하는 데이터와 모델을 평가하는데 사용하는 데이터가 달라야
모델의 예측 성능을 제대로 평가할 수 있다

학습/테스트 데이터 분리 방법

무작위가 일반적

시계열 데이터

과거에서 미래를 예측하려고 하는 경우
과거를 훈련 데이터로, 미래를 테스트 데이터로

다중선형회귀모델

1. 기준모델 (특성feature 없음)
2. 단순선형회귀 모델을 만들고 (특성feature 한 개 사용)
3. 2개 이상의 특성feature들을 사용하는 다중선형회귀모델

1 -> 2-> 3 순서대로 mae(오류)가 줄어둠

회귀모델 평가지표(evaluation metrics)

MSE(Mean Squared Error)

가장 많이 사용

• 단점

1. (제곱해서) 단위스케일이 변하기 때문에, 오류의 정도를 확인하기 어려움
2. 이상치에 너무 큰 값이나 작은 값이 주는 영향 큼
   -> 이상치에 다른 평가지표들보다 민감하다

MAE(Mean Absolute Error)

단위 스케일 동일 -> 오류를 직관적으로 판단 가능

RMSE (Root Mean Squared Error)

$\sqrt{MSE}$
MSE에 루트 -> 단위 스케일을 맞춤
MSE의 단점을 개선

R-squared (Coefficient of determination)

결정계수 $R^2$

회귀모델의 설명력을 표현하는 지표
$R^2=1$ : 데이터에 대한 설명력이 높다

• SSE(Sum of Squares Error, 관측치와 예측치 차이)
  $\sum_{i=1}^{n}\left(y_{i}-\hat{y}_{i}\right)^{2}$
• SSR(Sum of Squares due to Regression, 예측치와 평균 차이)
  $\sum_{i=1}^{n}\left(\hat{y}_{i}-\bar{y}_{i}\right)^{2}$
• SST(Sum of Squares Total, 관측치와 평균 차이)
  $\sum_{i=1}^{n}\left(y_{i}-\bar{y}_{i}\right)^{2} = SSE + SSR$

과적합(Overfitting)과 과소적합(Underfitting)

선형회귀모델

장점 : 다른 ML 모델에 비해 상대적으로 학습이 빠르고 설명력이 강함
단점 : 과소적합(underfitting)이 잘 일어남

일반화(generalization)

일반화 오차 : 테스트데이터에서 만들어내는 오차
일반화가 잘 된 모델 : 훈련데이터에서와같이 테스트데이터에서도 좋은 성능을 내는 모델

머신러닝과정 중에서 과적합은 피할 수 없는 문제
모델이 너무 훈련데이터에 과하게 학습(과적합)을 하지 않도록

일반화가 잘된 모델을 만드는 것이 목적

아무리 좋은 모델이더라도 데이터가 충분하지 않으면 일반화X
-> 그러나 대부분의 경우 데이터가 충분하지 않은 상황에서 예측 필요
-> 과적합, 과소적합 바탕으로 좋은 모델을 선택
-> 최적의 복잡도를 가지는 모델을 선택

과적합

모델이 필요 이상으로 복잡, 훈련데이터의 noise도 학습
-> test data에서 오차가 커짐

(표본이 가지고 있는 이상치나, 선에서 벗어난 잔차들까지 다 선이 가져갈 수 있도록 회귀모델을 만드는 것

주어진 데이터를 기반으로 학습한 뒤 새로운 데이터의 특성을 예측하고자 할 때에, 주어진 데이터의 특성을 너무 세세하게 반영하여서 새로운 데이터를 유연하게 파악하지 못하게 되는 문제)

훈련데이터에만 특수한 성질을 과하게 학습해 일반화를 못해
테스트데이터에서 오차가 커지는 현상

과소적합

모델이 너무 간단, 훈련데이터의 일반적인 성질들을 충분히 학습X
-> train data에서 조차도 안좋은 성능

련데이터에 과적합도 못하고 일반화 성질도 학습하지 못해,
훈련/테스트 데이터 모두에서 오차가 크게 나오는 경우

분산/편향 트레이드오프

과적합/과소적합은 오차의 편향(Bias)과 분산(Variance)개념과 관계 있음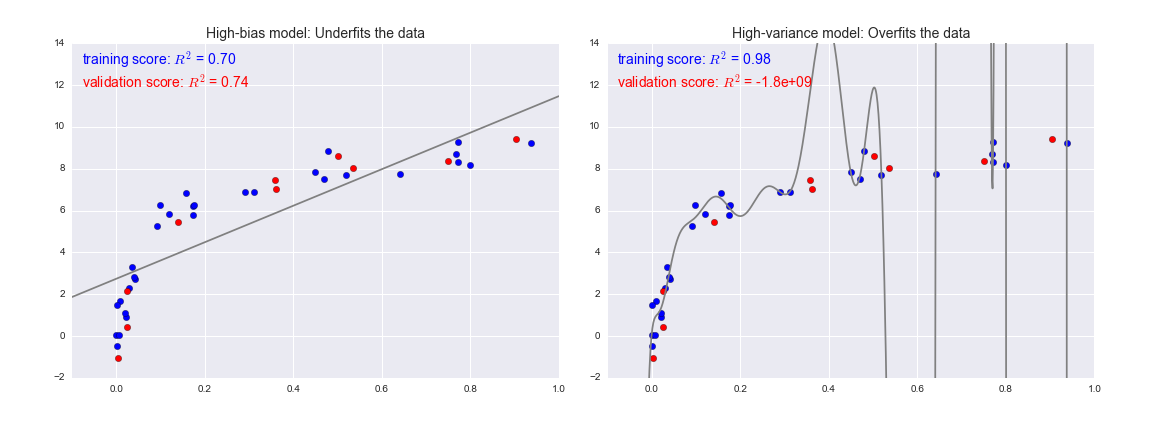high variance(데이터 셋의 종류에 따라 예측값 분산이 높을 때)= 과적합
high bias = 과소적합
*low variance : 여러 데이터셋에서 오차가 비슷한 것

• The Dangers of Under-fitting and Over-fitting

모델이 복잡해질 수록 훈련데이터 성능은 계속 증가
검증데이터 성능은 어느정도 증가하다가 증가세가 멈추고 오히려 낮아짐
-> 과적합이 일어나는 시점, 더 복잡한 모델은 불필요

어느 정도 이상으로 복잡도가 올라가면(특성을 많이 사용할수록) 과적합(high variance)
-> 일반화 성능 감소
ex) 모델 복잡도(차수degrees)가 올라갈 수록 과적합 되어 훈련 $R^2$ 값이 좋아지지만 테스트 $R^2$ 값은 줄어듦

MSE

reducible, irreducible 에러로 나누어 표현
reducible 에러 : Bias 에러 + Variance 에러

${\displaystyle \operatorname {E} _{D}{\Big [}{\big (}y-{\hat {f}}(x;D){\big )}^{2}{\Big ]}={\Big (}\operatorname {Bias} _{D}{\big [}{\hat {f}}(x;D){\big ]}{\Big )}^{2}+\operatorname {Var} _{D}{\big [}{\hat {f}}(x;D){\big ]}+\sigma ^{2}}$

${\displaystyle \operatorname {Bias} _{D}{\big [}{\hat {f}}(x;D){\big ]}=\operatorname {E} _{D}{\big [}{\hat {f}}(x;D){\big ]}-f(x)}$

${\displaystyle \operatorname {Var} _{D}{\big [}{\hat {f}}(x;D){\big ]}=\operatorname {E} _{D}[{\big (}\operatorname {E} _{D}[{\hat {f}}(x;D)]-{\hat {f}}(x;D){\big )}^{2}]}$

데이터의 노이즈, 데이터의 오류에 의한 에러(데이터 자체의 오류) : $\sigma^2$
-> 데이터 자체를 수정하지 않은 이상 어떤 모델을 써도 발생하는 오류

선형회귀모델

종속변수와 독립변수가 선형관계가 아니더라도, 각 독립변수들이 선형결합으로 연결
-> 다중 선형 회귀 모델
-> 선형 모델

• 비선형회귀모델
  -> 최소제곱법으로 fitting 할 수 없는 모델
  -> 회귀변수가 비선형일 때

다항회귀모델(polynomial regression)

Sklearn의 PolynomialFeatures 사용해서 구현
-> 다항 특성(polynomial features)을 방정식에 추가
*특성들의 상호작용을 보여줘서 상호작용특성(interaction features)이라고도 부름

과제관련 : How to select features