- 링크 : https://huggingface.co/papers/2505.24726
- 출간일 : 2025.05
- 저자 : Shelly Bensal∗ Umar Jamil∗ Christopher Bryant Melisa Russak Kiran Kamble Dmytro Mozolevskyi Muayad Ali Waseem AlShikh
1. Abstract
- 핵심 아이디어
- LLM이 문제에 실패하면 자기 성찰(self-reflection)을 작성한 뒤 다시 시도
- 다음 시도가 성공하면 모델이 작성한 self-reflection token에만 보상을 부여
- Reflect → Retry → Reward 구조
- Reflect : 모델이 실패한 이유를 자기 성찰 텍스트로 작성
- Retry : 성찰을 포함한 상태로 동일한 문제 재시도
- Reward : 시도가 성공하면 성찰 텍스트에 보상
- 이 구조를 반복하며 일반적인 사고력 강화
- 성능 향상
- 수학 방정식(math equation writing)에 대해 34.7% 성능 향상 (최고 사례)
- 함수 호출(function calling)에 대해 18.1% 성능 향상 (최고 사례)
- 자기 성찰 훈련을 한 소형 모델(1.5B ~ 7B)이 10배 이상 큰 모델보다 좋은 성능을 보이기도 함
2. Introduction
- 그동안의 문제점
- 그동안 LLM은 많은 발전을 해왔음
- 하지만 그러한 발전에도 불구하고 여전히 사각지대가 존재하며, 한번 성공했다고 해서 비슷한 유형의 테스크 또한 성공할거라는 보장은 없음
- 그동안의 대안
- 가장 직접적인 해결책은 해당 실패 사례에 대한 데이터로 재학습 또는 파인튜닝을 하는것 → 하지만 적절한 데이터셋이 없거나 생성이 어려운 경우가 많음
- 대안으로는 모델이 self-reflect을 하도록 프롬프트를 만들어 주는 방법이 있다.
- 대표적인 예시가 CoT이고 성능을 올려주는게 입증되었음
- 이 접근방식의 핵심적인 장점은 추가적인 훈련 데이터가 필요하지 않음
- 하지만 그 효과는 reasoning/reflection 프롬프트의 품질에 민감함
- 가장 직접적인 해결책은 해당 실패 사례에 대한 데이터로 재학습 또는 파인튜닝을 하는것 → 하지만 적절한 데이터셋이 없거나 생성이 어려운 경우가 많음
- 제안
- 모델이 첫 시도에서 테스크를 실패하면, self-reflection을 생성하고 이것을 두번째 시도에 사용하는 방식
- 만약 모델의 두번째 시도에서 성공하면, 정답이 아닌 self-reflection 토큰에 보상을 지급
- 이 방식의 장점은 작업별 데이터를 필요로 하지 않고, 대신 실수를 통해 개선 전략을 학습하게 만듦
- 특히, 성공/실패에 대한 이진 피드백만 있어도 적용 가능하다는 것이 큰 장점
3. Related Work
- Self-Reflection 관련 연구
- Self-reflection 또는 introspection은 모델이 스스로 자신의 reasoning을 검토하고 수정하는 방식
- 일반적으로는 다음의 과정을 따름:
- 답변 생성 → 피드백(비판 또는 자기 성찰) 생성 → 해당 피드백을 바탕으로 답변 수정
- 대표적인 사례로는 Chain-of-Thought(CoT) 방식이 있으며
arithmetic, commonsense reasoning, QA 등에서 성능 향상이 입증됨 - 다양한 방식이 존재:
- 실패했을 때만 self-reflect하거나, 모든 응답에 적용하기도 함
- 피드백은 점수, 자연어 설명, 외부 주석 등 다양한 형식 가능
- 피드백 제공 주체는 사람, 외부 모델, 또는 LLM 스스로일 수 있음
- 한계점:
- 모델이 스스로의 오류를 인식하지 못할 수 있음
- 반복할수록 효과가 줄어들 수 있음
- 쉬운 문제나 고성능 모델에서는 오히려 성능 저하 가능성 있음
- RL 기반 개선 방법 (GRPO 중심)
- 기존에는 PPO(Proximal Policy Optimization) 같은 강화학습 방식이 자주 사용됨
- 본 논문에서는 GRPO (Group Relative Policy Optimization)를 채택함
- critic 없이 여러 응답을 비교해 상대적으로 좋은 응답에 보상을 부여하는 방식
- 응답 전체가 끝난 후에야 보상을 주는 작업에 적합 (e.g. 수학 문제, 함수 호출)
- GRPO는 최근 여러 연구에서 self-correction, 도구 사용, 수학 문제 등 복잡한 작업에 효과적임이 확인됨
4. Reflect, Retry, Reward
- Mechanism
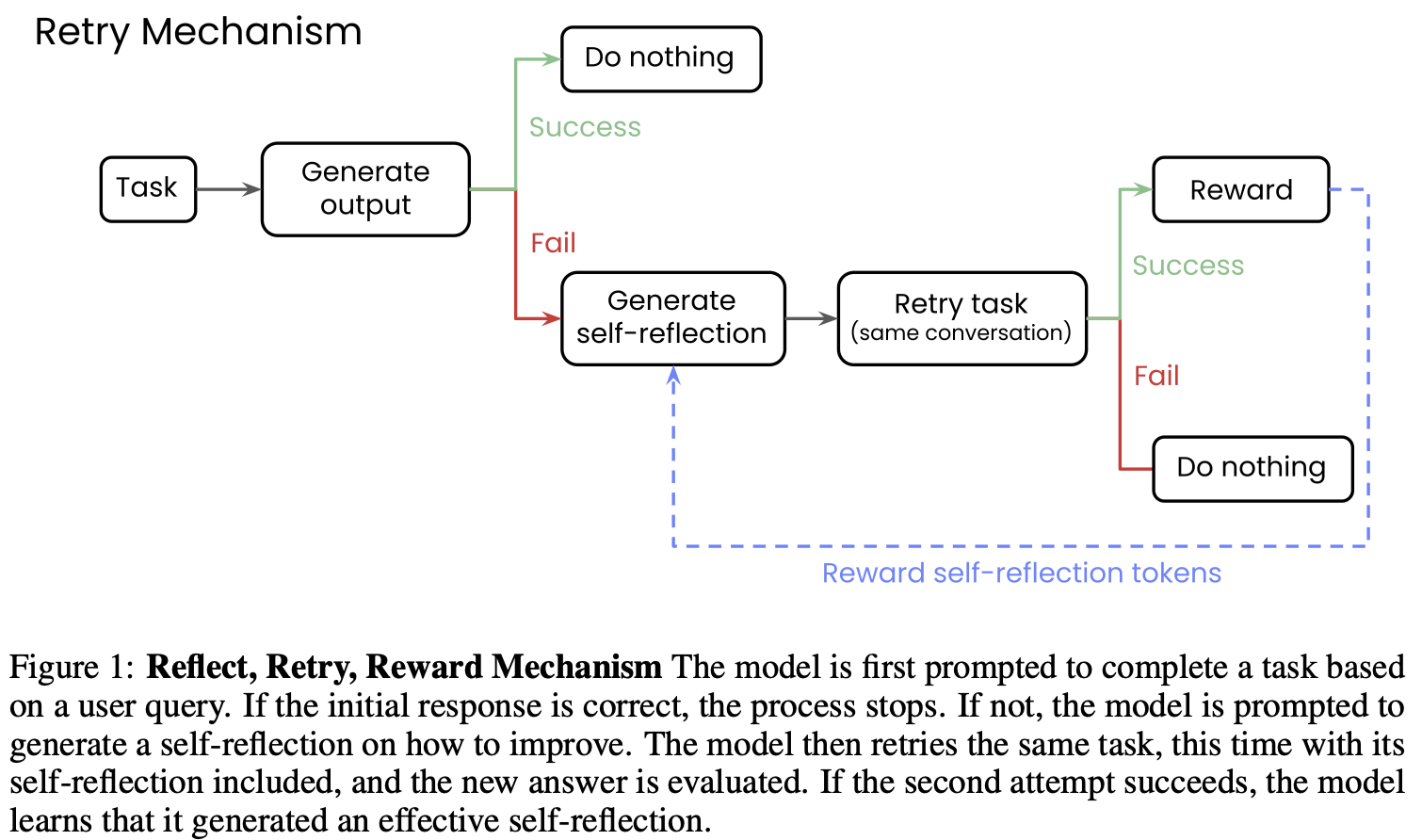
- ✅ 성공할 경우
- 결과를 그대로 유지하며, 추가 조치는 하지 않음
- ❌ 실패한 응답의 경우:
- 모델이 어떤 점이 잘못됐는지 self-reflection을 작성하도록 프롬프트 설정
- 이는 응답이 성공인지 실패인지 자동으로 평가하는 validator(검증자)를 전제로 한다는 점에 유의해야 함
Validator(검증자)에 대한 설명
- 모델의 응답이 성공/실패인지 자동으로 판단하려면 validator(검증자)가 필요함
- 일부 작업은 정답 레이블 없이도 validator를 만들 수 있음
예시:
- API 호출: 유효한 응답이 반환되었는가?
- 수학 문제: 결과가 목표값과 일치하는가?
- 코드 생성: 코드가 실제로 실행되는가? - 하지만 일부 작업은 정답 레이블(gold-standard answers)이 꼭 필요함
→ validator만으로는 성공 여부 판단이 어려운 경우도 있음
- 🔁 모델은 self-reflection을 대화 히스토리에 포함해 동일한 테스크를 다시 시도
- ❌ 두 번째 시도도 실패한 경우:
- 해당 self-reflection은 도움이 되지 않은 것으로 간주하고 아무런 보상도 주지 않음
- ✅ 두 번째 시도에서 성공한 경우:
- 정답 응답에는 보상을 주지 않음
- 오직 self-reflection 토큰에만 GRPO 방식으로 보상
- 이유: 특정 문제 풀이보다 전반적인 self-reflection 능력을 향상시키기 위함
5. Experiments
- function calling과 math equations의 경우로 실험을 진행함
5-1. Function Calling
- APIGen 데이터셋을 사용
- 사용자 쿼리(평문)
- 사용 가능한 도구 목록 + 각 도구의 파라미터 (JSON)
- 올바르게 포맷된 함수 호출(JSON)
- 총합 60,000개의 고품질 데이터
- 데이터셋 특성
- 총 4,211개의 고유 도구
- 도구당 평균 2.3개의 파라미터
- 쿼리당 평균 2.8개의 도구 중 선택하여 사용(최소 1, 최대 8)
- 정답 기준
- 정확한 도구 선택 + 정확한 파라미터와 값
- 평가 모델
- 실험에서 평가한 모델
- Qwen2 (1.5B, 7B Instruct)
- Llama3.1 (8B Instruct)
- Phi3.5-mini Instruct
- 비교용 대형 모델
- Qwen2-72B
- Llama3.1-70B
- Palmyra X4
- 실험에서 평가한 모델
- 모델별 프롬프트 최적화
- 모델마다 도구 호출 방식이 다름
- 서로 다른 프롬프트 템플릿으로 실험하고 가장 성능 좋은 포맷 채택
→ self-reflection 생성을 위한 프롬프트 (Reflect → Retry → Reward 중 Reflect 단계)
5-2. Countdown Math Equations
- DeepMind Countdown Dataset 사용
- 기존 CoT 논문에서도 사용된 수학 문제 데이터셋
- 입력 숫자들을 이용해 목표 숫자를 만들도록 유도하는 계산 문제
- 예시 문제
- 입력: [4, 73, 4, 23]
- 사용 가능 수식 : (+, -, *, /)
- 목표: 76
- 정답 기준
- 모델이 생성한 식을 실제로 계산했을 때 목표값과 정확히 일치해야 정답
- 평가 모델
- 실험에서 평가한 모델
- Qwen2 (1.5B, 7B Instruct)
- Llama3.1 (8B Instruct)
- Phi3.5-mini Instruct
- 비교용 대형 모델
- Qwen2-72B
- Llama3.1-70B
- Palmyra X4
- 실험에서 평가한 모델
→ self-reflection 생성을 위한 프롬프트 (Reflect → Retry → Reward 중 Reflect 단계)
5-3. A Dataset of Failures
- 목적: self-reflection 효과를 더 면밀히 분석하기 위해, 모델이 실패한 케이스만 모은 데이터셋 구성
- 구성 방식
- Function Calling 및 Countdown Math 실험에서 1차 시도에 실패한 문제만 수집
- 해당 문제들에 대해 self-reflection을 생성하고 두 번째 시도를 평가
- 활용 목적
- self-reflection이 실패를 얼마나 잘 보완하는지 확인 가능
- 실패 유형 및 분포 분석에 유용
5-4. Multi-Step GRPO
- 기존 GRPO의 한계
- 기존 방식은 1회 self-reflection + 1회 retry만 허용
- 그러나 많은 경우 한 번의 reflection만으로는 충분치 않음
- 개선 방식
- 실패 시마다 새로운 self-reflection 생성 → 재시도
- 총 4번까지 반복 시도 가능
- 보상 기준
- 성공한 시도의 마지막 self-reflection에만 보상 부여
- 이전 실패 reflection에는 보상 없음
6. Experimental Results
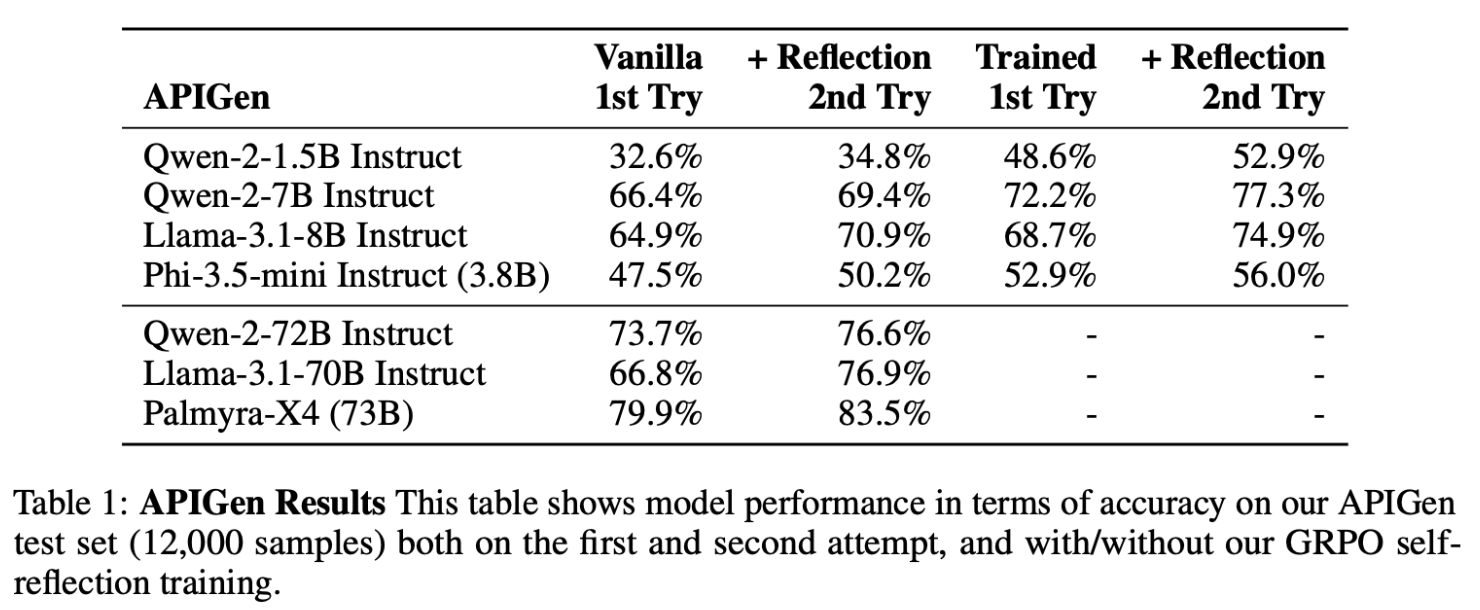
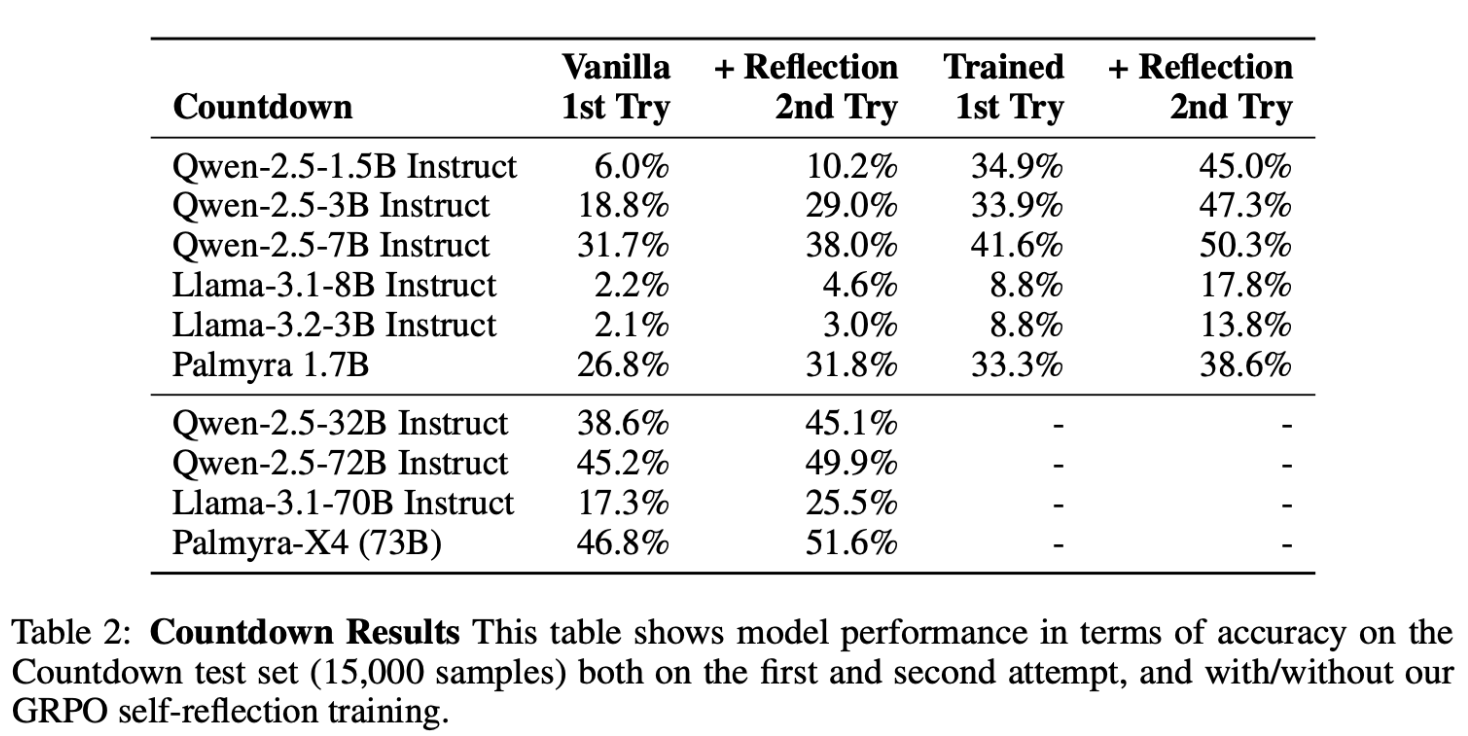
- 실험 테이블
- Table 1: APIGen 데이터셋 (12,000개 샘플)
- Table 2: Countdown Math 데이터셋 (15,000개 샘플)
- APIGen 실험 주요 결과
- 첫 시도에서는 모델 크기와 성능이 비례함
- self-reflection을 포함한 두 번째 시도에서 평균 4.5% 향상
- GRPO 학습 이후, 대부분 모델이 1회 시도만으로도 기존 2회 시도보다 더 나은 성능 달성
- 이는 self-reflection 학습이 모델의 전반적인 reasoning 능력을 강화했기 때문으로 해석됨
- GRPO 학습 이후에도 self-reflection을 활용하면 추가로 평균 4.7% 향상
- Qwen2-7B 모델이 GRPO 학습을 통해 Qwen2-72B(vanilla) 모델보다 우수한 성능 달성
- Countdown Math 실험 주요 결과
- 전체적으로 성능이 낮았으며, 특히 Llama 모델 계열의 성능 저조
- Llama-3.1-70B 모델조차 Qwen-2.5-3B보다 성능이 낮았음
- 성능 향상 패턴은 Function Calling(APIGen)과 유사했지만 향상 폭은 더 큼
- GRPO 학습 전 self-reflection으로 평균 5.3% 향상
- GRPO 학습 후 self-reflection으로 평균 8.6% 향상
- 성능 향상이 큰 이유는 모델의 초기 성능이 낮아 학습 여지가 컸기 때문
- 전체적으로 성능이 낮았으며, 특히 Llama 모델 계열의 성능 저조
6-1 Better Self-Reflections
- Figure 2를 통해, GRPO 학습 전후 self-reflection의 질적 차이를 비교함
- GRPO 학습 이후의 self-reflection은 더 짧고 간결하며, 반복이 줄어듦
- 이는 인간이 선호하는 방식과도 유사하지만, verbose한 CoT 방식과는 대조적임
- "언제 간결한 출력이 더 효과적인가?"는 향후 연구 과제로 남겨둠
6-2 Low Catastrophic Forgetting
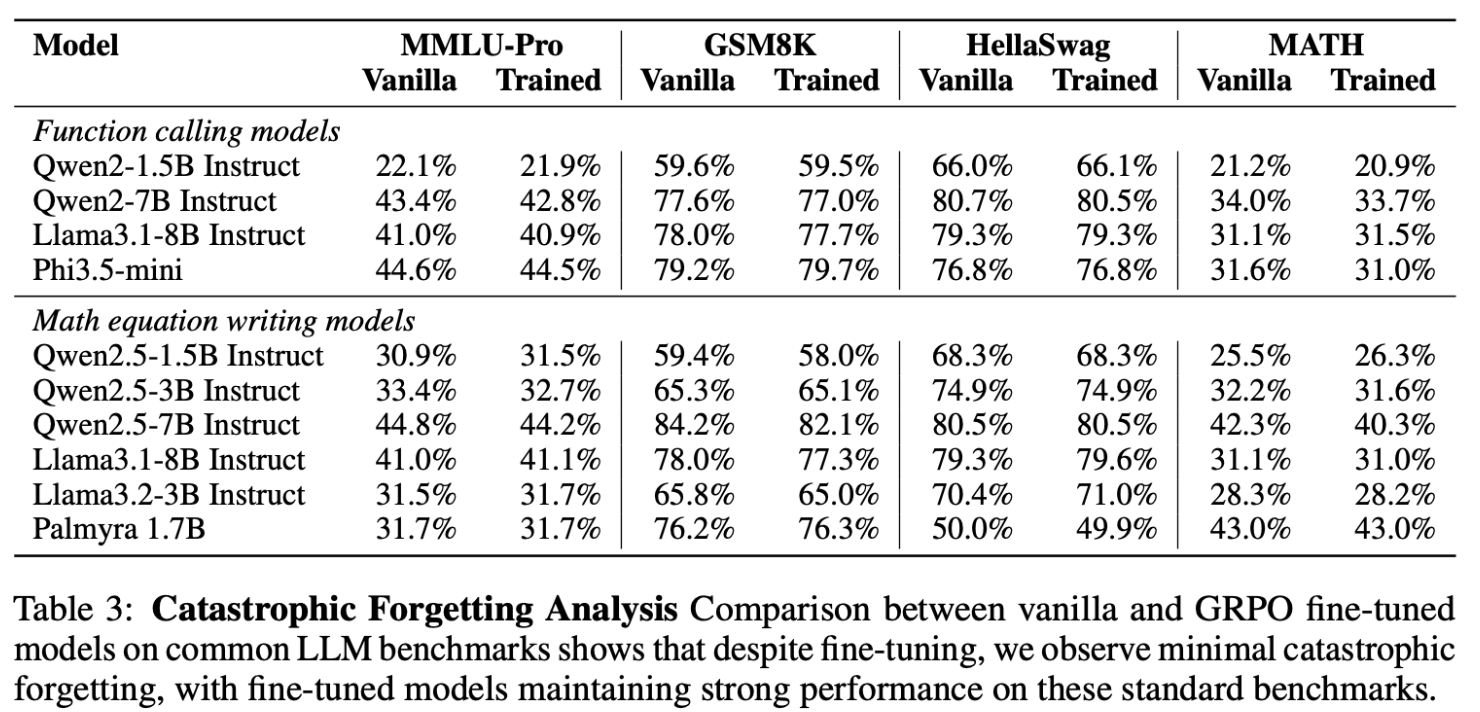
- Self-reflection 학습이 다른 작업(task) 능력에 부정적 영향을 주는지 확인하기 위해 다양한 태스크(MMLU-Pro, GSM8K, HellaSwag, MATH)로 평가함
- 대부분 성능 변화는 1% 미만으로 안정적이었고, 일부 모델은 오히려 성능이 향상됨
- Qwen-2.5-1.5B 모델은 MMLU-Pro(+0.6%), MATH(+0.8%) 향상
- 결론적으로, 본 방법은 catastrophic forgetting 없이 적용 가능함
7. Conclusion
- 핵심 성과
- self-reflection으로 LLM 성능 대폭 향상 (이진 검증기만 필요)
- 전체적으로 함수 호출 9.0%, 수학 방정식 16.0% 성능 개선
- 소형 모델이 대형 모델 능가: Qwen-7B(훈련) > Qwen-72B(미훈련)
- 주요 발견
- self-reflection이 필요 없는 첫 시도에서도 성능 향상
- 전반적 추론 능력 개선 효과 (치명적 망각 없음)
- 검증 가능한 태스크에 적합 (코딩, 수학, API 호출 등)
8. Limitations
- 검증기 정의의 어려움
- 모든 태스크에 이진 성공/실패 검증기 정의가 어려움
- 해결책: 정답 레이블 활용 또는 대형 모델을 validator(검증자)로 사용
- 모델 제약사항
- 기본 능력 필요: 태스크 수행 + self-reflection + self-correction
- 실패 사례: Llama3.2-3B는 함수 호출 self-correction 실패
- 적용 범위 한계
- 객관적 검증 가능한 태스크에만 적용
- 창의적/주관적 태스크에는 직접 적용 어려움
