0.코드를 저장한 깃허브 주소
https://github.com/guraudrk/bootcampcode_Deeplearning_pytorch
1.DNN (Deep Neural Network)
신경망 구성요소
dnn과 mlp와 ann이 서로 같은 것이다.
이들을 선형회귀 함수들을 사용하는 것이다.
2.train 프로세스
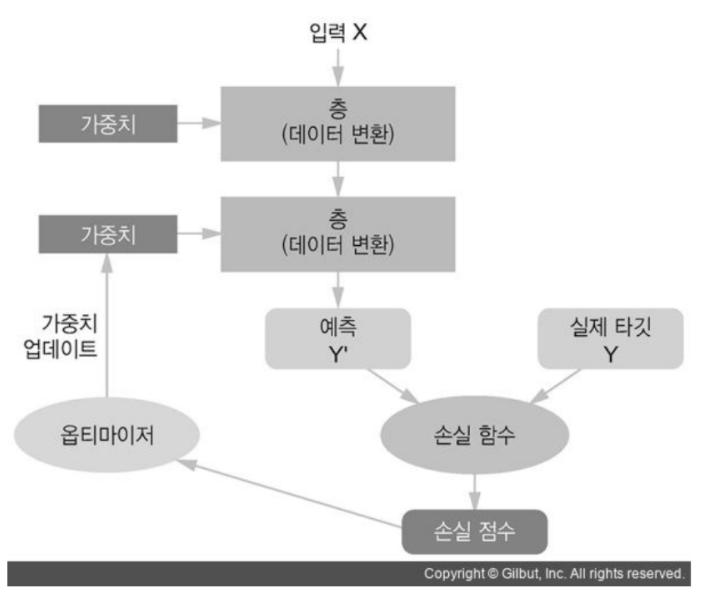
위의 그림을 잘 보도록 하자.
위의 그림에는 특기할만한 특징이 있다.
모델,손실함수,옵티마이저 등이 있다는 것이다.
3.역활
model/network
기존 데이터의 패턴을 학습해 새로운 데이터를 추론하기 위한 알고리즘.
loss function
학습 할 때 모델이 추론한 결과와 정답 간의 손실을 계산한다.
optimizer
학습할 때 loss function이 계산한 loss를 기반으로
loss가 줄어들도록 모델들의 parameter들을 업데이트해서 모델의 성능을 최적화한다.
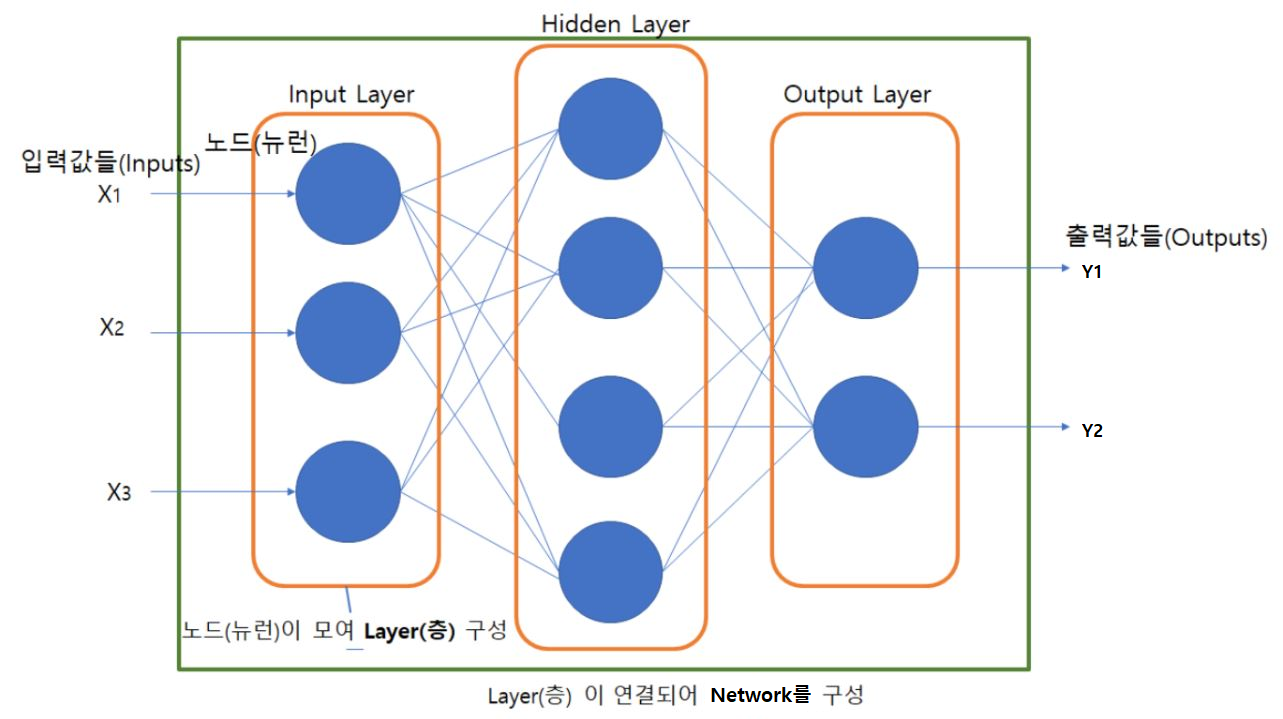
4.unit, node, neuron
input data를 입력받아 처리 후 출력하는 데이터 처리하는 함수이다.
은닉층 unit 들을 입력으로부터 추론을 위한 주요 특성들을 찾아 출력한다.
출력층의 유닛들은 추론 결과를 출력한다.
input data의 feature들에 가중치를 곱하고 편향을 더한 결과를
activation 함수에 넣어 출력하는 계산을 처리한다.
4.레이어/층
네트워크 모델의 각 처리단계를 정의한 함수이다.
실제 처리를 담당하는 unit들을 모아놓은 구조이다.
입력층, 출력층, 은닉층이 있다.
대부분 층들은 학습을 통해 최적화할 parameter를 가진다.
그런데 이 중 parameter 가 없는 층도 있다.
layer들을 연결한 것을 network이라고 한다.
딥러닝은 layer들을 깊게 쌓은 것을 말한다.
목적이나 구현 방식에 따라 다양한 종류들의 layer 들이 있다.
Fully Connected Layer (Dense layer)
추론 단계에서 주로 사용
Convolution Layer
이미지 Feature extraction으로 주로 사용
Recurrent Layer
Sequential(순차) 데이터의 Feature extraction으로 주로 사용
Embedding Layer
Text 데이터의 Feature extraction으로 주로 사용
5.모델
layer를 연결한 것이 딥러닝의 모델이다.
이전 레이어의 출력을 input으로 받아 처리한 뒤 output으로 출력하는 레이어들을 연결한다.
적절한 구조를 찾는 것은 공학적이기보다는 경험적인 접근이 필요하다.
6.활성 함수(Activation Function)
각 유닛이 입력과 weight간에 가중합을 구한 뒤 출력결과를 만들기 위해 거치는 함수이다.
문제에 맞추서 이 활성 함수를 정하는 것이 중요하다.
많은 함수 중에서 ReLU 함수를 주로 사용한다.
ReLU 말고도 sigmoid라는 함수를 한번 보자.
7.시그모이드 함수
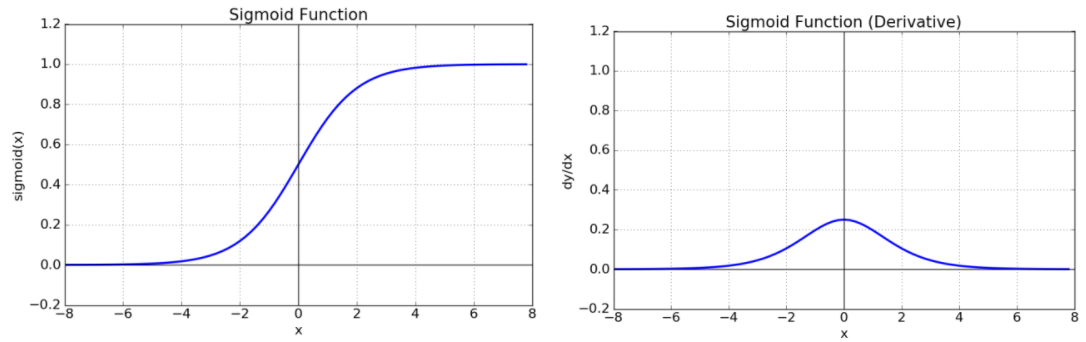
아래는 시그모이드 함수의 특징을 간단명료하게 설명한 것이다.
1.출력값의 범위가 0부터 1까지이다.
2.초기 딥러닝의 은닉층의 활성함수로 많이 사용되었다.
3.층을 깊게 쌓을 경우 기울기 소실(gradient가 0이 되어서 가중치들이학습이 안되는 현상)이라는 문제를 발생시켜 학습이 안되는 문제가 있다.
4.이진 분류를 위한 활성함수로 사용이 된다. 이는 출력값이 0,1밖에 없기 때문이다.
이 외에도 Hyperbolic tangent,Softmax 등의 활성화 함수들이 있다.
8.ReLU 함수
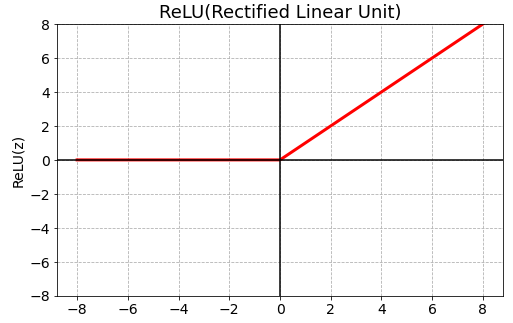
기울기 소실 문제를 어느 정도 해결이 되었다.
0이하의 값들에 대해 뉴런이 죽는 단점이 있다.
가장 많이 쓰이는 함수이다.
기울기 소실 문제를 해결했기 때문이다.
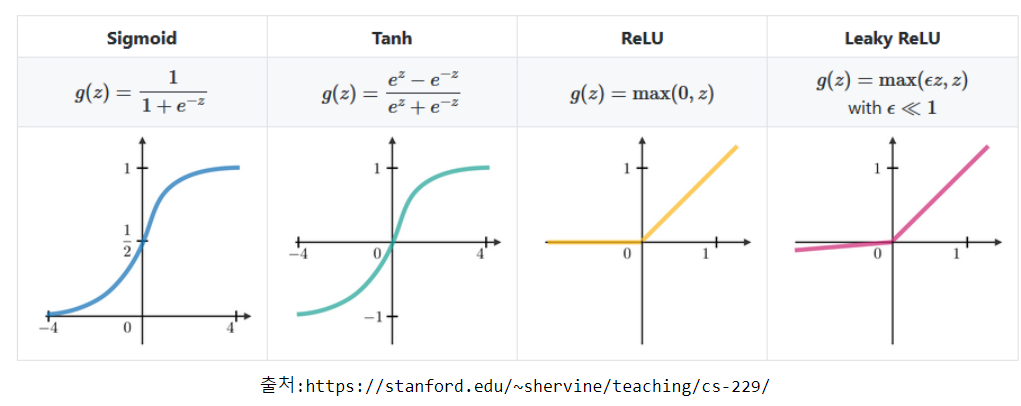
9.여러가지 함수들의 그래프
그래프 뿐만 아니라 식들을 알 수 있으므로 그림을 잘 보도록 하자.
10.손실함수
MODEL이 출력한 예측값과 실제 데이터간의 차이를 계산하는 함수이다.
중요한 것은 해결하려는 문제의 종류에 따라 표준적인 Loss Function이 있다는 것이다.
11.분류의 종류
2가지가 있다.
1.이진 분류(Binary classification)
2.다중 클래스 분류(Multi-class classification)
복잡한 식과 설명이 있는데, 필자는 이를 단순화할 것이다.
이진 분류 ---- 말해 yes or no
다중 클래스 분류 ----- n지선다형
12.회귀
연속형 값을 예측한다.
뭐 예를 들면 주가를 예측한다거나, 부동산의 가격을 예측한다거나이다.
(필자는 광교 고오급 아파트 오너가 될 것이다.----정말 쓸데 없는 사담 ^^)
뭐 암튼 연속된 값을 예측한다고 볼 수 있다.
Mean squared error 를 loss function으로 사용한다.
식은 대강 이렇게 된다.
𝐿𝑜𝑠𝑠(𝑦̂ (𝑖),𝑦(𝑖))=12(𝑦̂ (𝑖)−𝑦(𝑖))2
(𝑦(𝑖)
: 실제 값(Ground Truth), 𝑦̂ (𝑖)
: 모델이 예측한 값)
13.문제별로 출력레이어 Activation 함수, Loss 함수 등이 정해져 있다.
어떤 상황에서 어떤 것을 쓸 것인지 파악만 해 두고, 쓸 때 잘 쓰는 것이 중요하다.
14.경사하강법
최적화를 위해 파라미터들에 대한 Loss function의 Gradient값을 구해 Gradient의 반대 방향으로 일정크기 만큼 파라미터들을 업데이트 하는 것을 경사하강법이라고 한다.
사실 이렇게 딱딱하게 보는 것 보다는 식으로 직접 보는 것이 좋다.
𝑊𝑛𝑒𝑤=𝑊−𝛼∂∂𝑊𝐿𝑜𝑠𝑠(𝑊)
𝑊:파라미터𝛼:학습률
15.오차역전파
딥러닝 학습시 파라미터를 최적화 할 때 추론한 역방향으로 loss를 전달하여 단계적으로 파라미터들을 업데이트한다.
Loss에서부터(뒤에서부터) 한계단씩 미분해 gradient 값을 구하고 이를 Chain rule(연쇄법칙)에 의해 곱해가면서 파라미터를 최적화한다.
출력에서 입력방향으로 계산하여 역전파(Back propagation)라고 한다.
추론의 경우 입력에서 출력 방향으로 계산하며 이것은 순전파(Forward propagation)이라고 한다.
16.파라미터 업데이트 단위
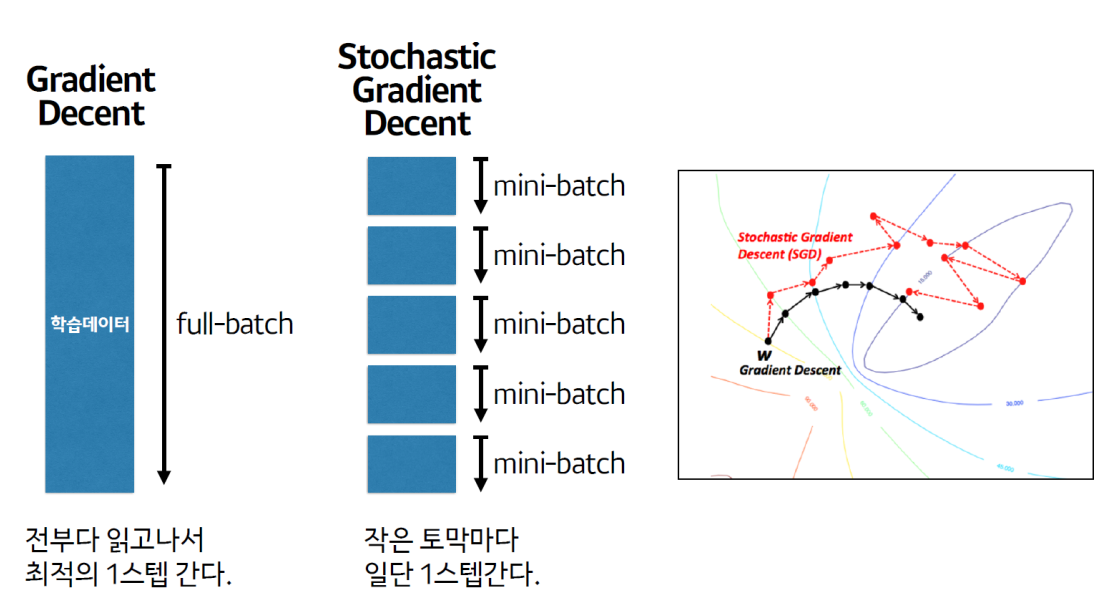
1.Batch Gradient Decent (배치 경사하강법)
전부 다 읽고 나서, 최적의 1스텝을 간다.
안정적이라는 장점이 있으나, 속도가 느리다.
약간 돌다리를 두들겨서 건너는 느낌이라 그렇다.
2.Mini Batch Stochastic Gradient Decent (미니배치 확률적 경사하강법)
작은 토막마다 일단 1스텝을 간다.
계산은 빠른 장점이 있으나 그 과정이 중구난방일 수 있다.
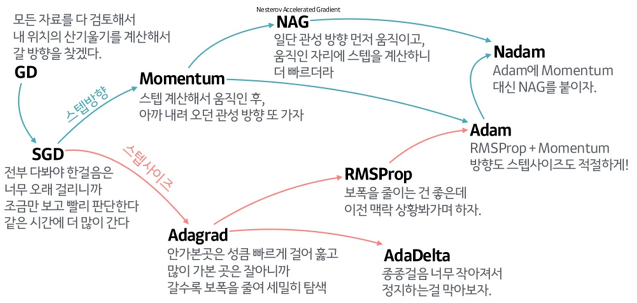
17.주요 옵티마이저
여러가지 옵티마이저가 있다.
잡다한 것들이 굉장히 많은데, 우리는 이 중
adam,sgd 같은 것을 보면 된다. 다 세세하게 알 필요는 없다.
18.심심할 때 아래의 사이트를 보면서 딥러닝에 대한 개념을 익히자.
