
• PFH(포인트 특징 히스토그램)
• FPFH(빠른 포인트 특징 히스토그램)
• RSD(반경 기반 표면 설명자)
• 3DSC(3D 형상 컨텍스트)
• SHOT(방향 히스토그램 서명)
• NARF(정렬 정렬 방사형 기능)
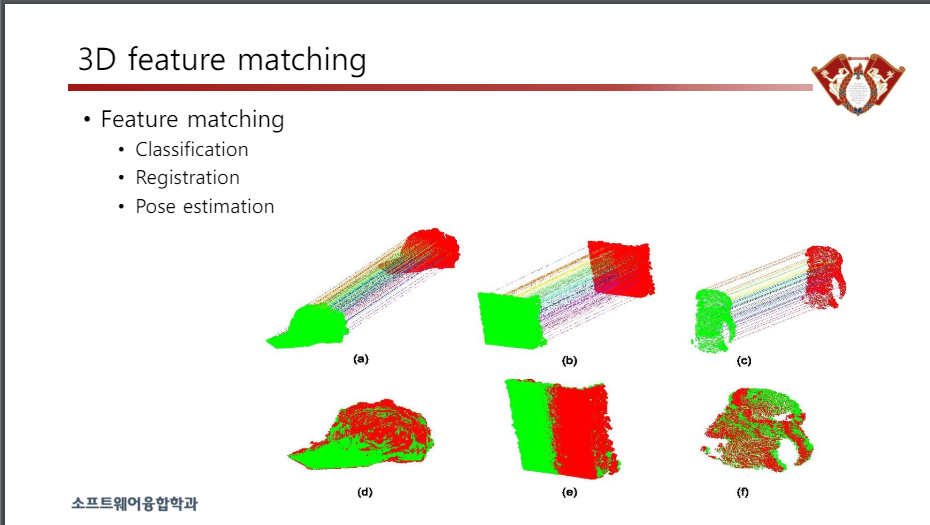
3D 특징 매칭
• 기능 매칭
• 분류
• 등록
• 포즈 추정
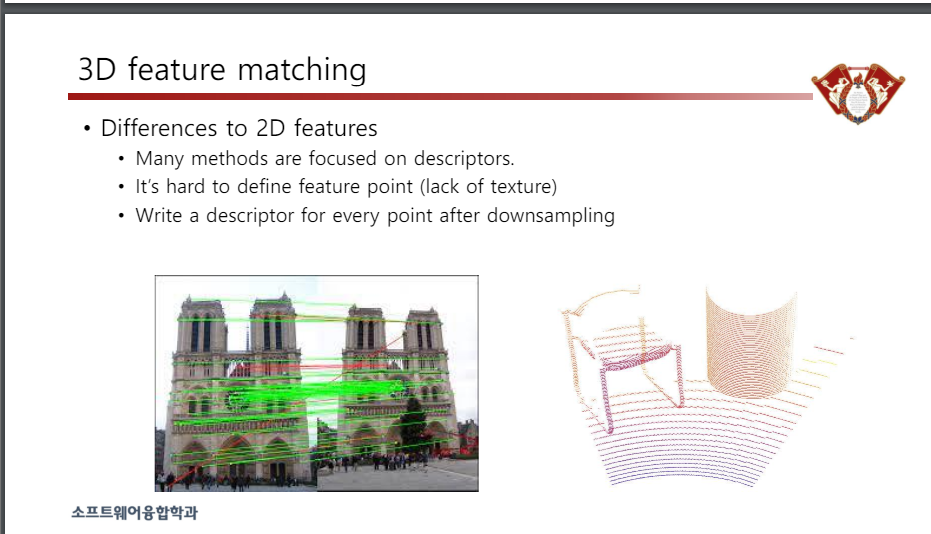
2D 기능과의 차이점
• 많은 방법이 설명자에 중점을 둡니다.
• 특징점 정의가 어렵다(텍스처 부족)
• 다운샘플링 후 모든 포인트에 대한 설명을 작성합니다.
2D Feature 와 3D Feature 의 차이점
3D point cloud 는 2D 이미지와 다르게 Feature point 를 정의하기가 어렵습니다.
3D point cloud 를 다룰 때는 Feature Point 를 추출하지 않습니다. 이미지에는 Harris Corner, DOG, FAST 등으로 Feature 를 추출하는데, 3D point cloud 에서는 왜 Feature Point 를 추출하지 않는 것일까요 ?
이미지는 어떤 값으로든 2차원 행렬이 가득 차있고, 따라서 이미지들은 Texture 가 풍부하다고 할 수 있습니다.
2차원 이미지에서는 Feature 를 찾기가 쉽고, Feature 들이 많이 나옵니다. 따라서 2차원 이미지에서는 Feature 를 뽑는 것이 유의미한 행위입니다.
하지만 Point Cloud 에서는 컬러값이 없기 때문에 Feature 를 뽑는 것이 매우 어려울 뿐 아니라 충분할 만큼 많은 양의 Feature 가 뽑히지도 않습니다.
따라서 대부분의 알고리즘들은 3D point cloud 에서 특징점을 뽑기보다는 포인트들의 Descriptor 를 만드는 것에 집중되어 있습니다.
그런데, Descriptor 라는 것은 "어떤 포인트가 기준으로 주어졌을 때 , 주어진 포인트들에 대해 Descriptor" 를 만드는 것이기 때문에 "특징점을 뽑지 않으면 어떻게 Descriptor 를 만드는 것일까 ? " 라는 생각을 할 수 있습니다.
대답은 다음과 같습니다.
모든 Point 들에 대해서 Descriptor 를 다 만듭니다.

• 3D 기능(설명자)은 다음과 같아야 합니다.
• 변화에 강함
• 강체 변환은 형상에 영향을 주어서는 안 됩니다.
• 소음에 강함
• 노이즈를 유발하는 측정 오류로 인해 특징 추정이 크게 변경되어서는 안 됩니다.
• 해상도 불변
• 다른 밀도로 샘플링한 경우(예: 다운샘플링 수행 후) 결과는 동일하거나 유사해야 합니다.
3D Descriptor 의 조건
Robust to transformations
Point Cloud 가 Rotation / Translation 되어도 같은 위치에서 Feature 가 뽑혀야 합니다.
가까이서 찍던 멀리서 찍던 같은 점에 대해서는 늘 같은 Descriptor 가 나와야 합니다.
Robust to noise
Resolution invariant
Point Cloud 는 보통 Downsampling 을 해서 많이 사용하는데, Downsampling 을 하여도 동일한 Descriptor 가 나와야 합니다.

• 로컬 설명자는 개별 포인트에 대해 계산됩니다.
• 객체가 무엇인지에 대한 개념은 없으며 단지 해당 지점 주변의 로컬 기하학이 어떻게 되는지를 설명합니다.
• 특징 포인트
• 다운샘플링 및 나머지 모든 포인트 선택
포인트 클라우드의 경우, 가지고 있는 정보는 "어떤 포인트와 다른 포인트 간의 기하학적 관계" 뿐입니다.
따라서 요약하자면 다음과 같습니다.
- Point Cloud Descriptor 를 다룰 때, Feature Extraction 은 하지 않는다.
- 모든 포인트들에 대해서 Descriptor 를 만든다.
- Descriptor 는 Point 들 간의 Geometry 를 이용해서 만든다.

PFH (Point Feature Histogram)
• 지점 주변의 기하학적 정보를 캡처합니다.
• 주변 법선의 방향 차이 분석
• 알고리즘은 근처의 모든 지점을 쌍으로 연결합니다.
• 고정 좌표계는 법선으로부터 계산됩니다.
• 법선 간의 차이는 3개의 각도 변수로 인코딩될 수 있습니다.
• 3개의 각도 변수 + 점 사이의 유클리드 거리
• 모든 인접 쌍이 계산 → 히스토그램으로 비닝
PFH (Point Feature Histogram)
이것은 Point Cloud Descriptor 중의 원조격이라고 할 수 있는 알고리즘입니다. 이 알고리즘은 점과 그 점 주변에 있는 포인트들 간의 기하학적 관계를 통해서 정보를 취득합니다.
이때 주변 포인트와의 관계를 통해서 얻을 수 있는 정보는 Normal 정보 (법선 벡터)입니다.
포인트들 마다 normal 벡터의 방향이 조금씩 다르기 때문에, 이 normal 방향의 차이점을 분석해서 어떤 점에 대한 Descriptor 를 만드는 것이 PFH 입니다.

• 법선 벡터 추정
• 가장 간단한 방법을 사용하는 것은 1차 3D 평면 피팅을 기반으로 합니다.
• 𝑃𝑘: p와 k-이웃으로 구성된 포인트 클라우드.
• 법선 벡터 𝑛는 𝑃𝑘로 구성된 평면에 수직입니다.
• 고유값이 가장 작은 고유벡터가 법선벡터이다 𝑛
• 구형 좌표로 표시:

모든 점들에 대해서 normal vector 를 구한 것

PFH 알고리즘은 Vicinity (일정 반경 내에 있는, 이웃하는 점들) 내의 모든 점을 pair 로 구해서, normal 의 차이점을
(3가지 각도에 관련한 값) + (포인트들 간의 Euclidean 거리)
로 나타냅니다. 이를 Quadreplet 이라고 합니다.
그리고 이렇게 얻은 Quadreplet 에 대한 Histogram 을 만듭니다
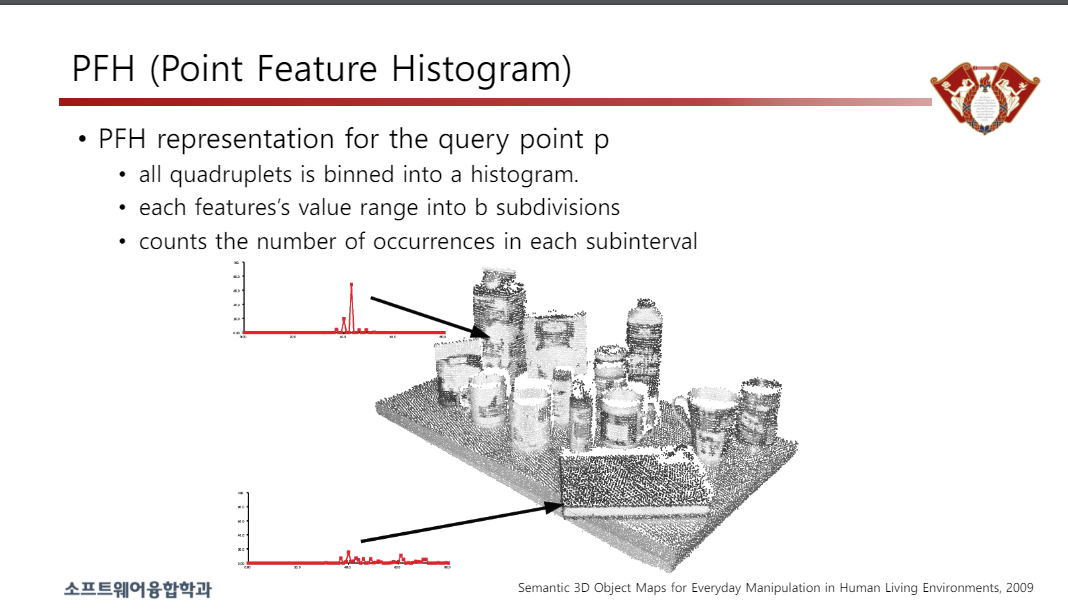
• 쿼리 포인트 p에 대한 PFH 표현
• 모든 네 쌍둥이는 히스토그램으로 분류됩니다.
• 각 기능의 값 범위를 b개로 세분화
• 각 하위 간격의 발생 횟수를 계산합니다.
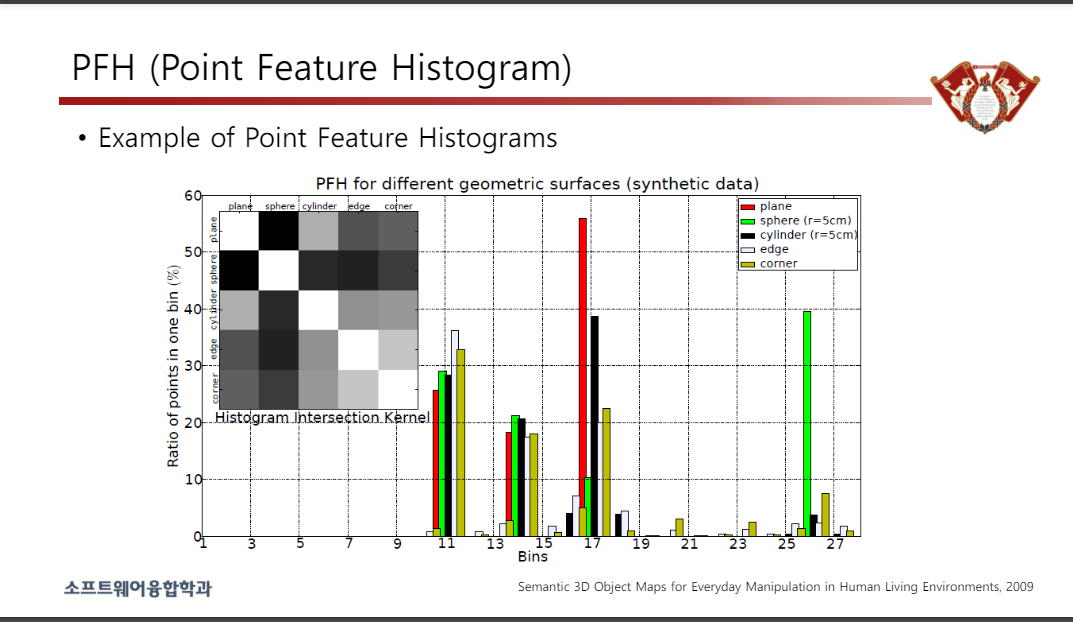

FPFH (Fast Point Feature Histogram)
• PFH는 정확한 결과를 제공하지만 단점이 있습니다.
• 실시간으로 수행하기에는 계산 비용이 너무 많이 듭니다.
• 𝑂(𝑛𝑘의 복잡성2).
• FPFH는 PFH의 복잡성을 줄입니다.
• 𝑂(𝑛𝑘)의 복잡성.
• FPFH는 𝑝𝑞의 모든 이웃을 완전히 상호 연결하지 않습니다.
• FPFH에는 r 반경 구 외부의 추가 점 쌍이 포함되어 있습니다.

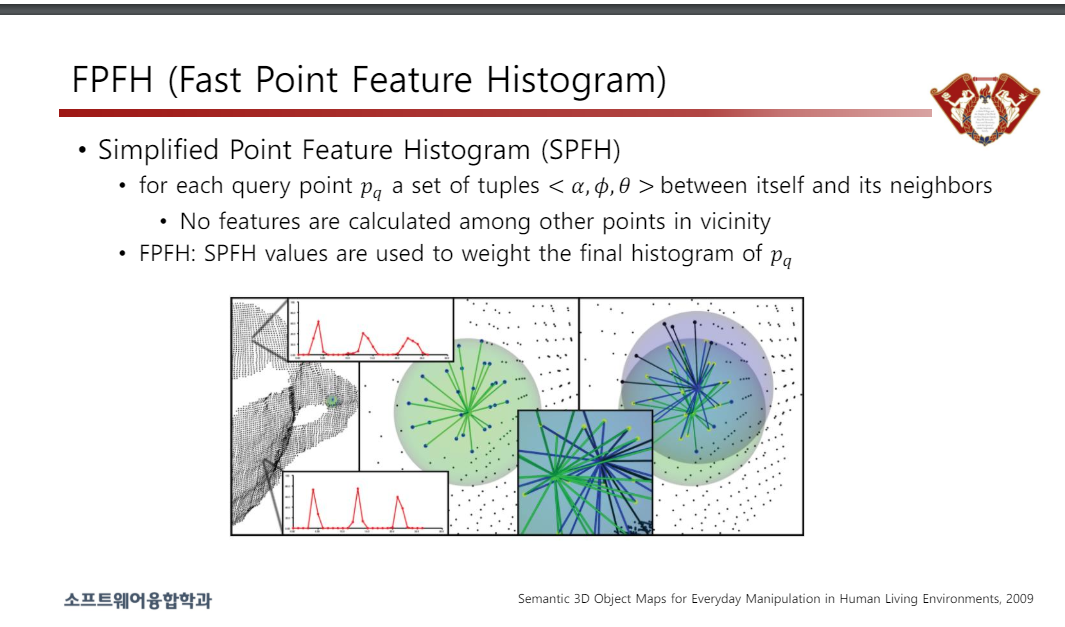
• 단순화된 포인트 특징 히스토그램(SPFH)
• 각 쿼리 포인트 𝑝𝑞에 대해 자신과 이웃 사이의 튜플 세트 < 𝛼,𝜙, 𝜃 >
• 주변의 다른 지점 간에는 어떤 특징도 계산되지 않습니다.
• FPFH: SPFH 값은 𝑝𝑞의 최종 히스토그램에 가중치를 부여하는 데 사용됩니다.
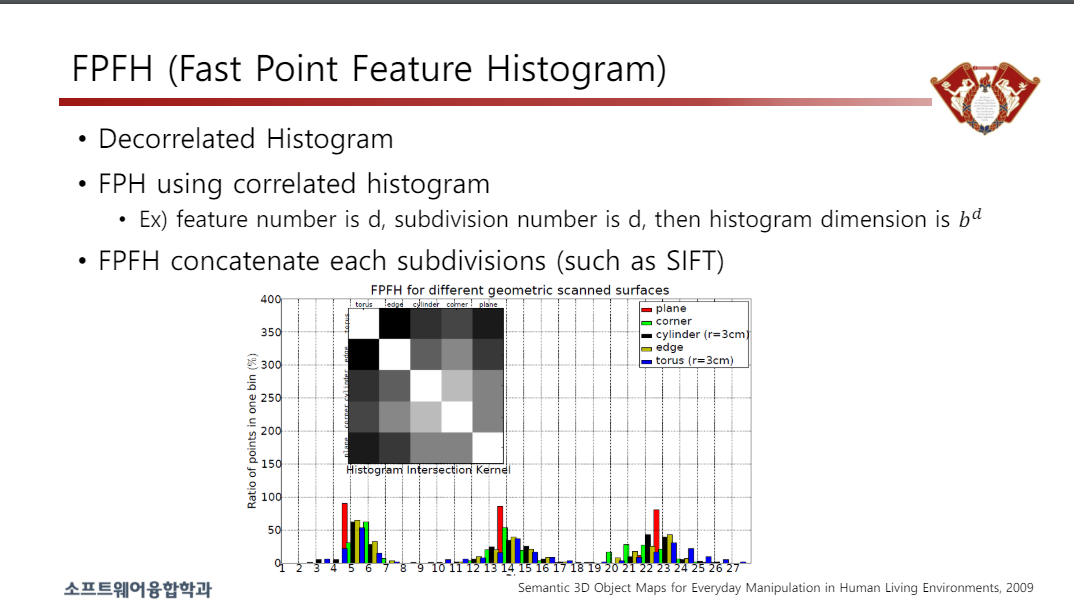
• 장식관련 히스토그램
• 상관 히스토그램을 사용한 FPH
• 예) 특징번호는 d, 분할번호는 d, 히스토그램 차원은 𝑏𝑑
• FPFH는 각 하위 구분(예: SIFT)을 연결합니다.
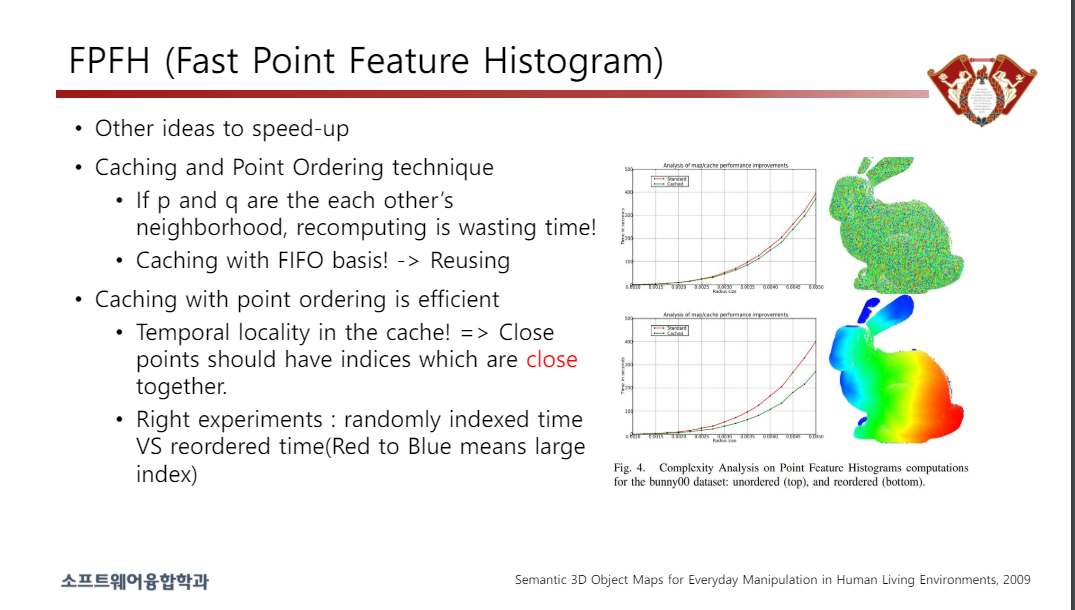
속도를 높이는 다른 아이디어
• 캐싱 및 포인트 주문 기술
• p와 q가 서로 이웃이라면 재계산은 시간 낭비입니다!
• FIFO 기반 캐싱! -> 재사용
• 포인트 순서를 사용한 캐싱이 효율적입니다.
• 캐시의 시간적 지역성! => 가까운 지점은 서로 가까운 인덱스를 가져야 합니다.
• 올바른 실험: 무작위로 색인된 시간 VS 재정렬된 시간(빨간색에서 파란색으로 갈수록 큰 색인을 의미)
3DSC
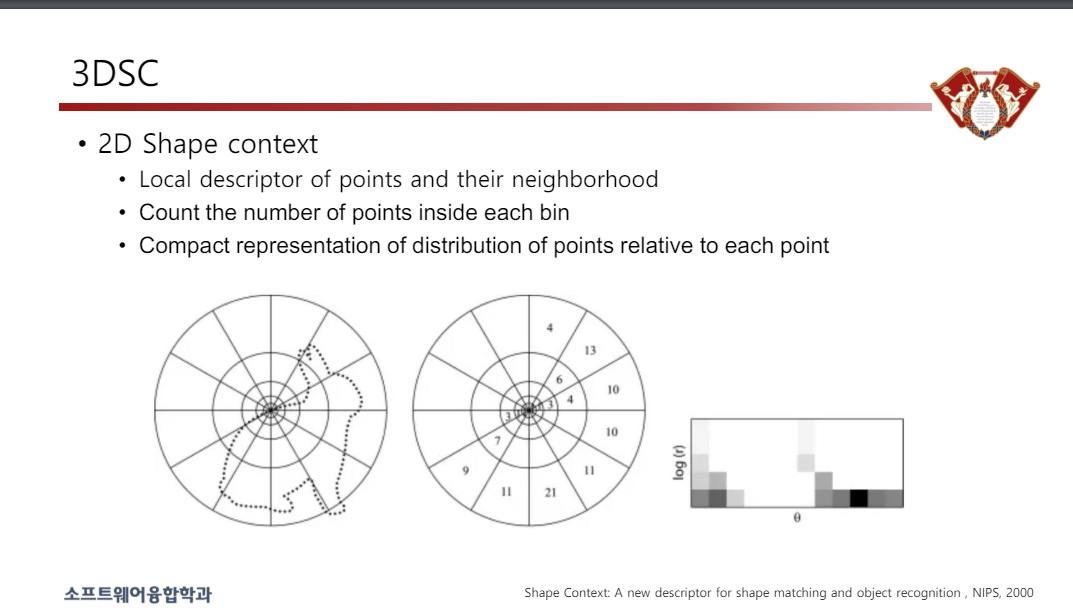
• 2D 도형 컨텍스트
• 지점과 주변 지역에 대한 지역 설명
• 각 저장소 내부의 포인트 수를 계산합니다.
• 각 포인트에 대한 포인트 분포를 간결하게 표현
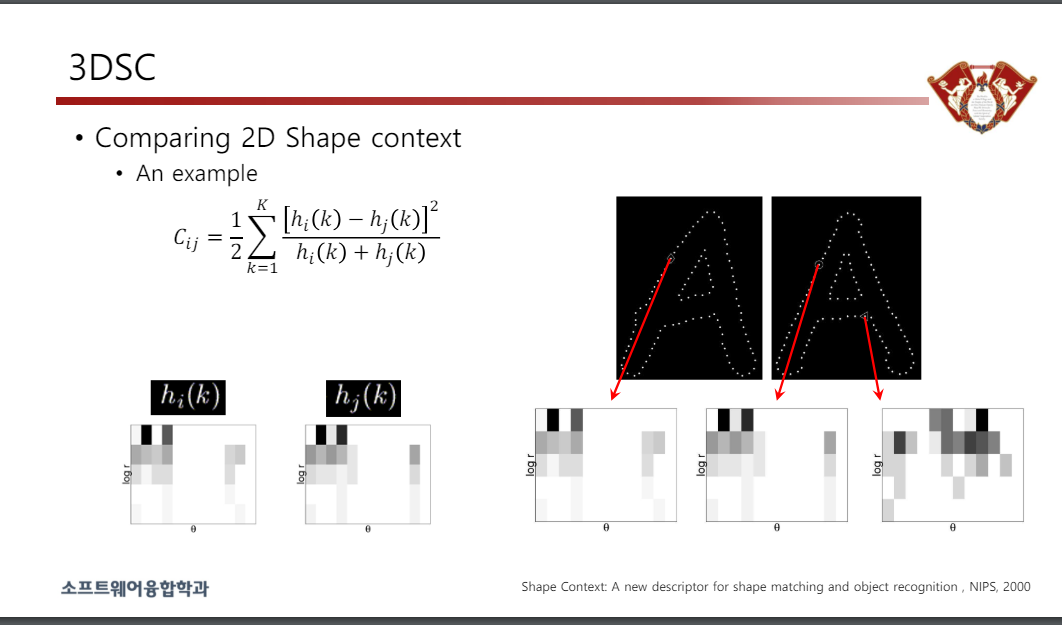
• 2D Shape 컨텍스트 비교

• 3D 도형 컨텍스트
• 3D Shape Context는 기존 2D 대응물을 3차원으로 확장하는 설명자입니다.
• 해당 구의 "북극" → 법선 벡터
• 평면 내 회전에 불변하지 않음
• 구는 3D 영역 또는 저장소로 나누어집니다.
• 2개 좌표(방위각 및 고도각): 동일한 간격
• 방사형 치수: 로그 간격

SHOT
• 방향 히스토그램 서명
• 구형 지지 구조를 사용하여 토폴로지(표면)에 대한 정보를 인코딩합니다.
• 모든 볼륨에 대해 1차원 로컬 히스토그램이 계산됩니다. → 회전 불변
• 구는 32개의 저장소 또는 볼륨으로 나뉩니다.
• 방위각을 따라 8개 분할
• 고도를 따라 2개
• 반경을 따라 2개
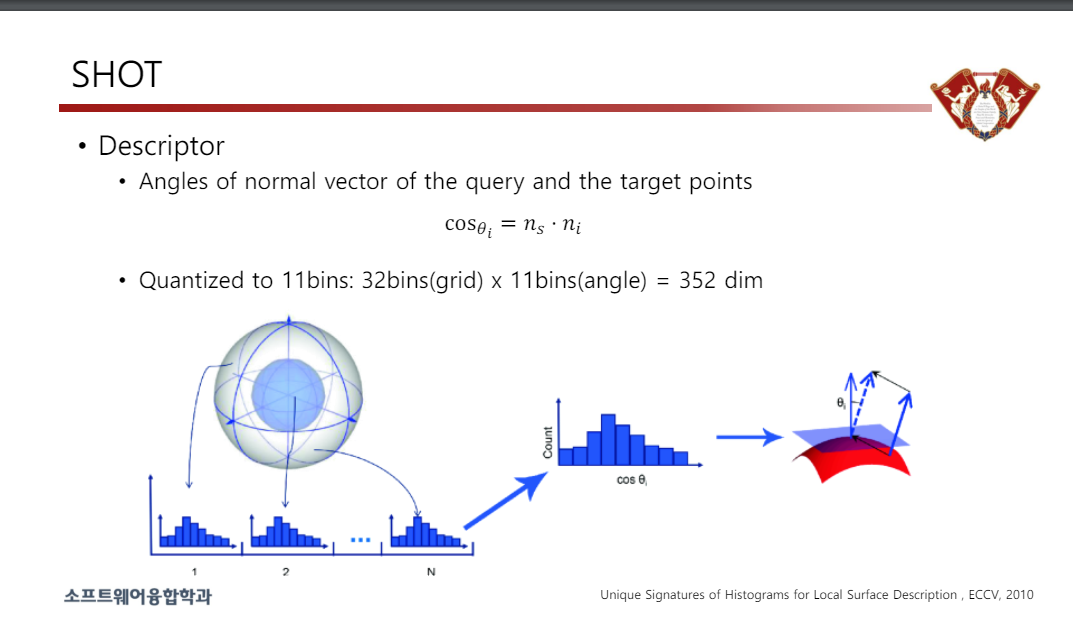
• 설명자
• 쿼리와 대상점의 법선 벡터 각도
• 11bin으로 양자화: 32bins(grid) x 11bins(angle) = 352 dark


NARF
• 법선 정렬 방사형 특징
• 객체 인식을 위한 3D 범위 이미지 기능
• 깊이 이미지 기반 방법
• 깊이를 나타내는 픽셀 값이 있는 2D 이미지
• 국경 추출 가능
• 경계선과 거리(픽셀) 값의 변화를 사용하여 핵심 포인트를 식별합니다.
• 핵심 포인트는 규모에 따라 변하지 않으며 카메라 방향에 영향을 받습니다.
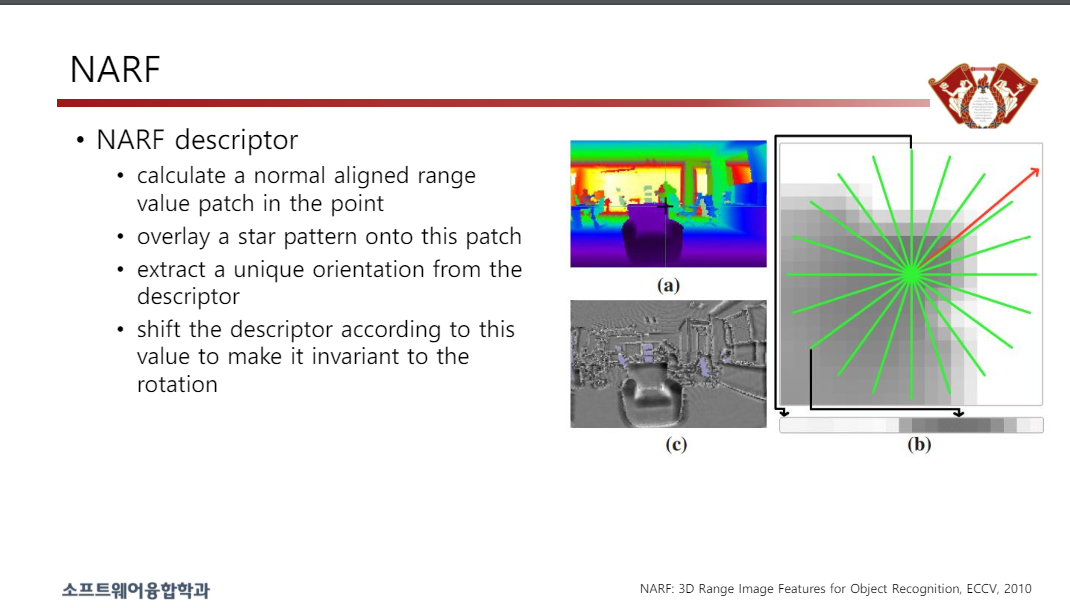
• NARF 설명자
• 포인트에서 일반 정렬 범위 값 패치를 계산합니다.
• 이 패치에 별 패턴을 오버레이합니다.
• 설명자에서 고유한 방향을 추출합니다.
• 이 값에 따라 설명자를 이동하여 회전에 불변하도록 만듭니다.