
1. 기하학적 변환(T2.6)
2. 이미지 등록(T2.6)
3. RANSAC(무작위 표본 합의)

1. Geometric Transformations
✓ 기하학적 변환
✓ 아핀 변환
✓ 관점 변환
✓ 기하변환: 1) & 2)단계
✓ 변환 행렬을 얻는 방법은 무엇입니까?
✓ 출력 이미지의 크기

◆ 이미지의 픽셀 공간 배열을 수정합니다.
◆ 두 가지 기본 작업으로 구성됩니다.
1) 좌표변환
★ (x, y) & (x', y')를 각각 입력 및 출력 이미지의 좌표라고 합니다.
★ 그러면 출력 좌표는 다음과 같이 계산될 수 있습니다:
2) 강도 보간
★ 공간적으로 변환된 이미지 픽셀에 강도 값을 할당합니다.

◆ Translation (이동변환)
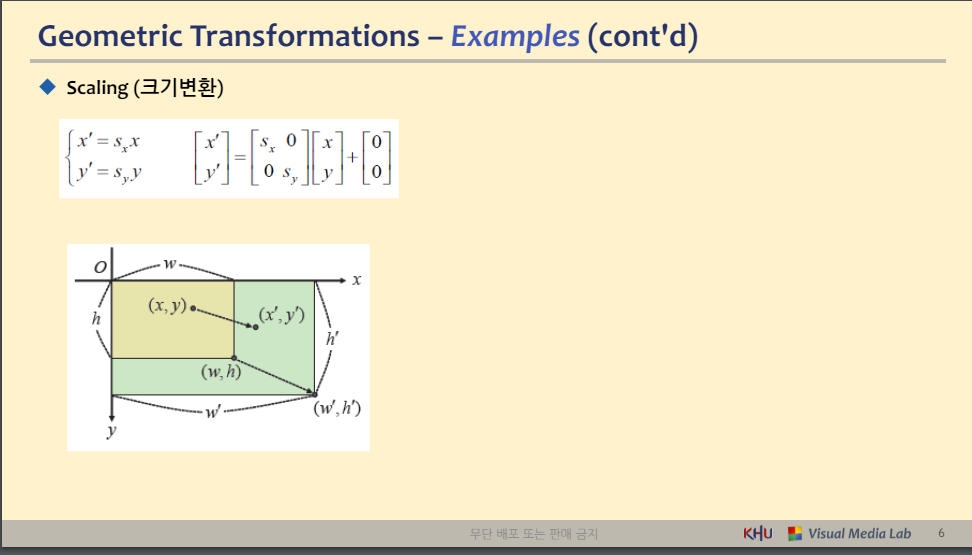
◆ Scaling (크기변환)
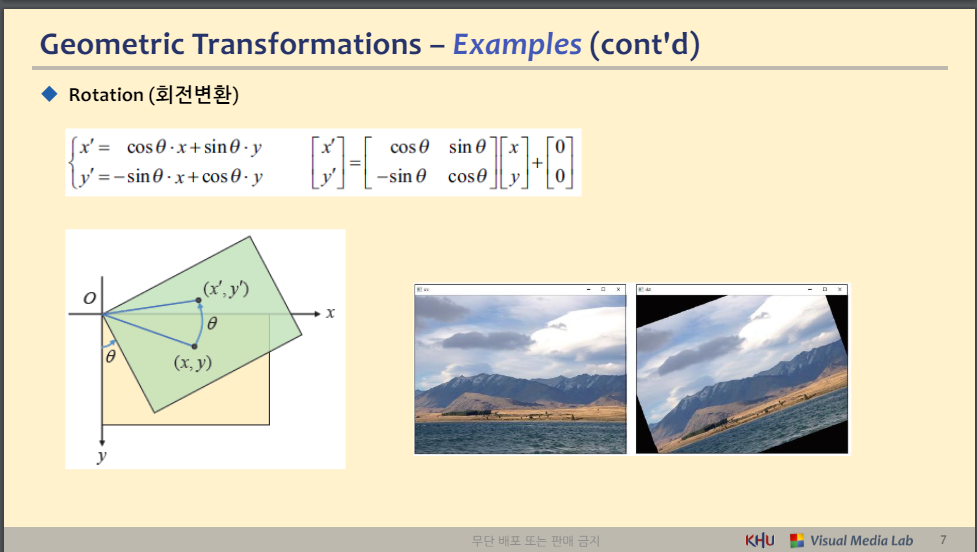
◆ Rotation (회전변환)

◆ Flipping (대칭변환)

◆ Shear (전단변환)

◆ 이동, 크기 조정, 회전, 반사(뒤집기), 기울이기 등이 포함됩니다.
◆ 이는 두 가지 형태로 표현될 수 있습니다.
1) 선형변환 + 오프셋(변환)
2) 아핀 매트릭스
◆ 6개 매개변수의 값을 결정하려면 최소 3쌍의 대응점이 필요합니다.

◆ 예: 동일성, 크기 조정, 반사, 회전

◆ 예: 평행이동, 수직 및 수평 전단

Affine Transformation – Property
◆ Affine 변환은 다음을 유지합니다.
⚫ 직선
⚫ 비행기
⚫ 병렬성
⚫ 평행선분의 길이 비율
◆ 다음 사항이 반드시 보존되는 것은 아닙니다.
⚫ 거리 및 각도
⚫ 참조) 직교 변환으로 거리와 각도 유지
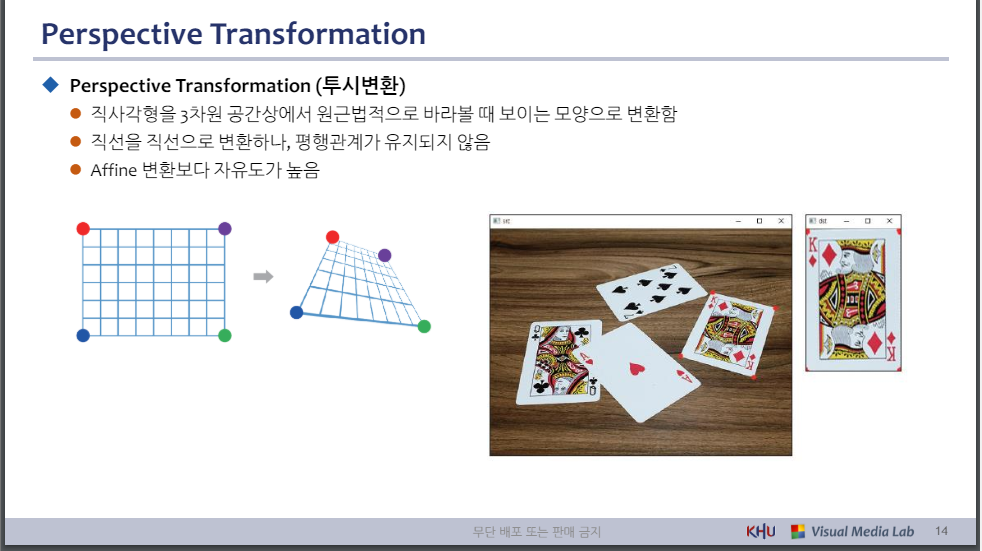
◆ Perspective Transformation (투시변환)

⚫ 투시 변환은 8개의 파라미터로 표현할 수 있음

Other Geometric Transform Models
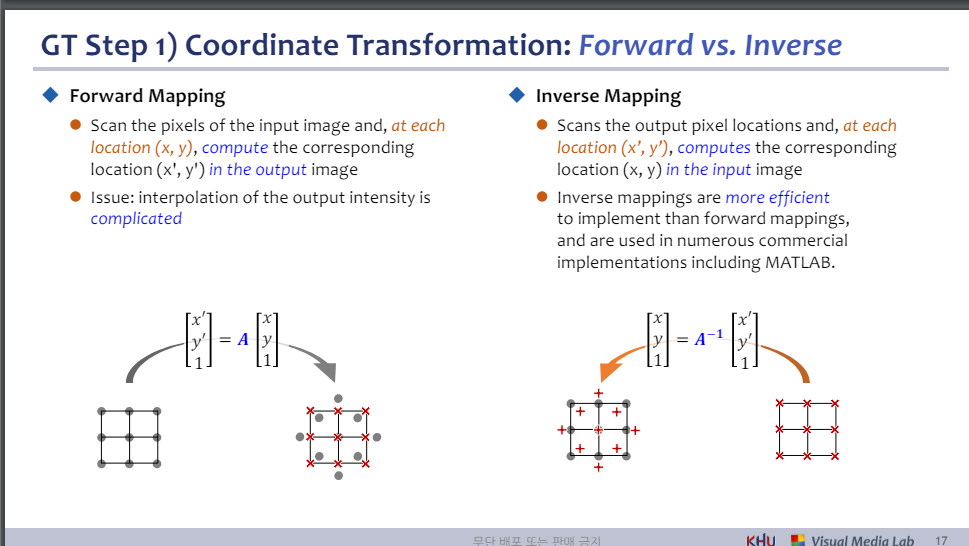
GT Step 1) Coordinate Transformation: Forward vs. Inverse
◆ 포워드 매핑
⚫ 입력 이미지의 픽셀을 스캔하고 각 위치(x, y)에서 출력 이미지의 해당 위치(x', y')를 계산합니다.
⚫ 문제: 출력 강도의 보간이 복잡함
◆ 역 매핑
⚫ 출력 픽셀 위치를 스캔하고 각 위치(x', y')에서 입력 이미지의 해당 위치(x, y)를 계산합니다.
⚫ 역 매핑은 순 매핑보다 구현이 더 효율적이며 MATLAB을 포함한 수많은 상용 구현에 사용됩니다.

GT Step 2) Intensity Interpolation
◆ ... 다양한 강도 보간 기술에 대해서는 "이미지 크기 조정" 강의를 참조하십시오.
그림 2.40 회전(-21˚) 및 보간
(a) 문자 T의 541 X 421 이미지
(b) 최근접 이웃 보간
(c) 이중선형 보간.
(d) 쌍삼차 보간.
(e)-(h) 확대된 섹션

How to Get the Transformation Matrix?
◆ (x', y') & (x, y)를 각각 입력 이미지와 참조 이미지의 연결점 좌표라고 합니다.
◆ 아핀 근사(6-매개변수 모델):
⚫ 두 이미지 모두에 3쌍의 기준점이 있는 경우 6개의 알려지지 않은 계수를 해결할 수 있습니다.
◆ 이중선형 근사(8개 매개변수 모델):
⚫ 두 이미지 모두에 4쌍의 기준점이 있으면 8개의 알려지지 않은 계수를 풀 수 있습니다.

Size of the Output Image
◆ 출력 이미지가 포함된 공간 직사각형의 크기가 원본 이미지의 직사각형보다 클 경우가 있습니다.
⚫ 예. 그림 2.41(b)
◆ 이 문제를 해결하기 위한 두 가지 옵션이 있습니다.
⚫ 그림 2.41(c)와 같이 회전된 이미지를 원본 이미지 크기와 동일하게 자릅니다. 또는
⚫ 그림 2.41(d)와 같이 전체 회전된 원본을 포함하는 더 큰 이미지를 유지합니다.
◆ 참고: 정의되지 않은 영역을 채우고 싶을 수도 있습니다.
⚫ 예. 그림 2.41(c)와 (d)의 검은색 픽셀
그림 2.41 (a) 디지털 이미지. (b) 회전된 이미지.
(c) 회전된 이미지는 원본 이미지와 동일한 영역에 맞게 잘립니다.
(d) 회전된 이미지 전체를 수용하기 위해 이미지가 확대되었습니다.
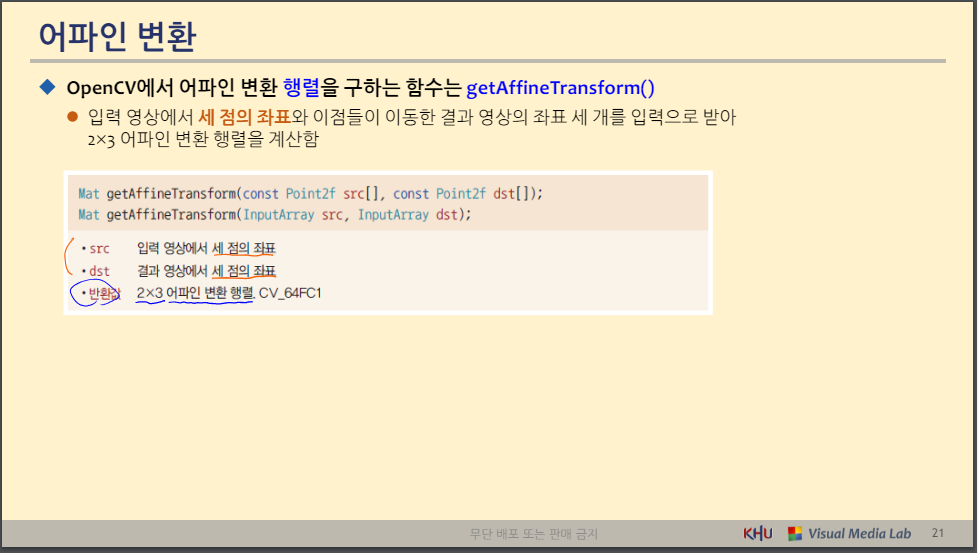
어파인 변환
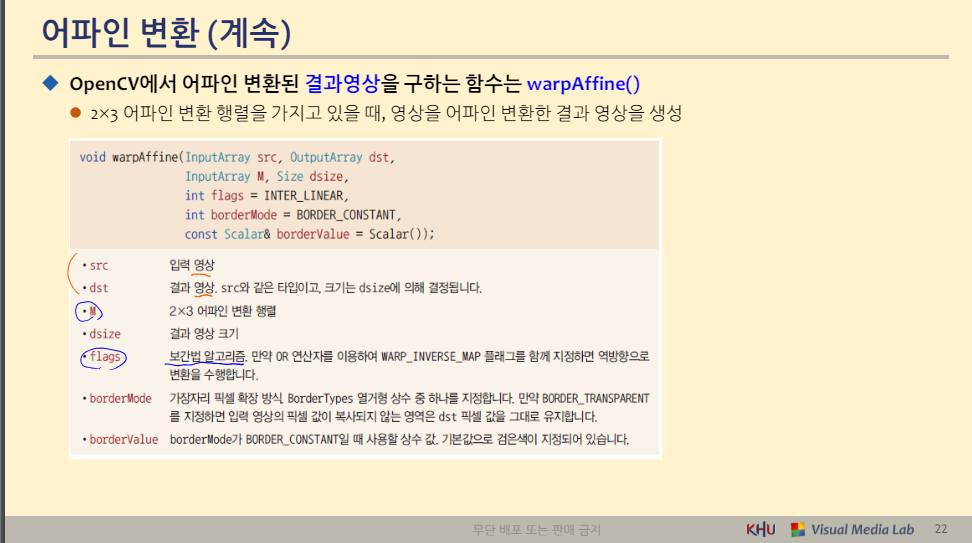
◆ OpenCV에서 어파인 변환된 결과영상을 구하는 함수는 warpAffine()
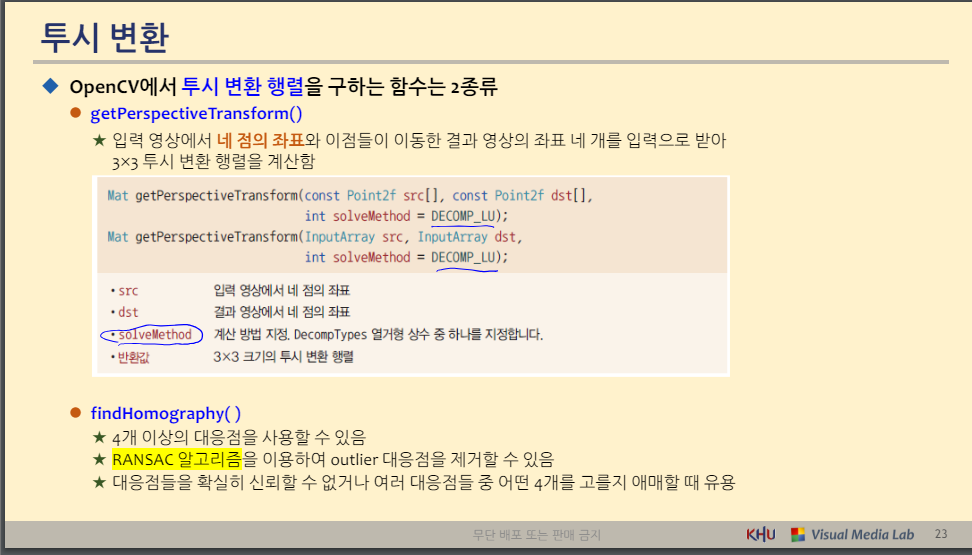
◆ OpenCV에서 투시 변환 행렬을 구하는 함수는 2종류
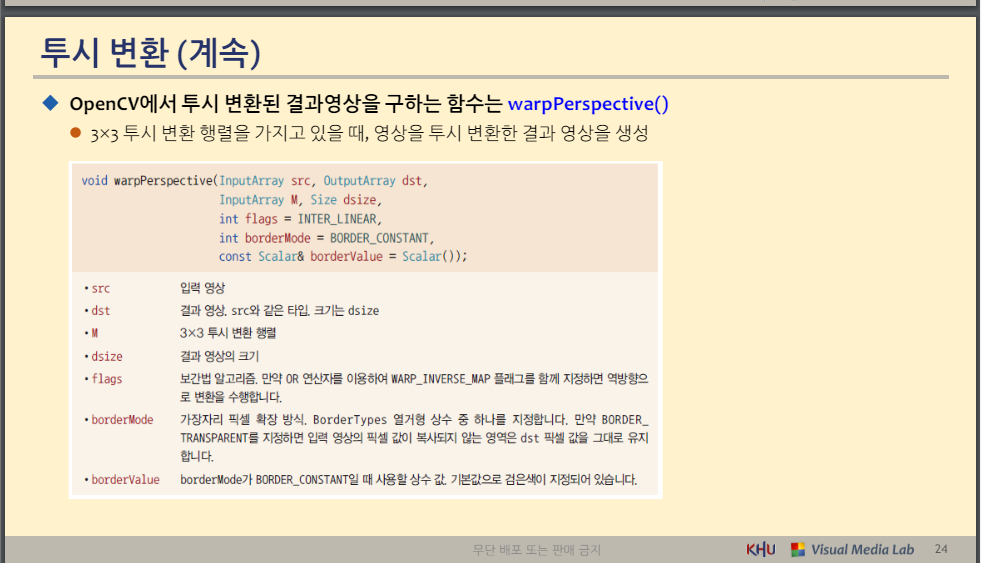
◆ OpenCV에서 투시 변환된 결과영상을 구하는 함수는 warpPerspective()

- Image Registration
✓ 정의
✓ 동점(Key Point)
✓ 기하학적 변환 추정
✓ 결과가 만족스럽지 못한 경우
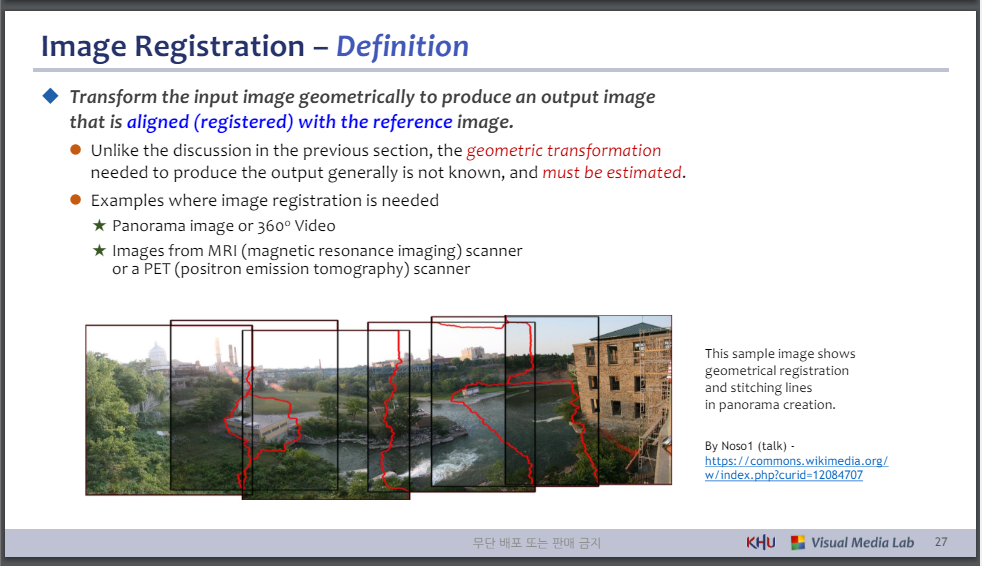
Image Registration – Definition
◆ 입력 이미지를 기하학적으로 변환하여 참조 이미지와 정렬(등록)된 출력 이미지를 생성합니다.
⚫ 이전 섹션의 논의와 달리 출력을 생성하는 데 필요한 기하학적 변환은 일반적으로 알려져 있지 않으며 추정해야 합니다.
⚫ 이미지 등록이 필요한 예시
★ 파노라마 이미지 또는 360o 비디오
★ MRI(자기공명영상) 스캐너 또는 PET(양전자방출단층촬영) 스캐너의 이미지
이 샘플 이미지는 파노라마 생성 시 기하학적 등록 및 스티칭 선을 보여줍니다.

Image Registration – Step 1) Tie Points Selection
◆ 타이 포인트(일명 컨트롤 포인트 또는 키 포인트)
⚫ 결점은 입력 및 참조 이미지에서 위치가 정확하게 알려진 해당 지점입니다.
⚫ 대화형(즉, 수동)으로 선택하거나 일부 알고리즘을 사용하여 자동으로 감지할 수 있습니다.
⚫ 일부 이미징 시스템에는 기준점 설정을 위한 가이드로 사용할 수 있는 일련의 알려진 지점이 있습니다.
◆ 핵심 포인트 탐지 알고리즘의 예:
⚫ 해리스 코너와 가우스 오브 해리스 코너의 차이점.
⚫ SIFT(Scale-Invariant Feature Transform) 및
SURF(강력한 기능 가속화).
★ 이 제품은 특허를 받았으며 상업적인 사용이 제한되어 있습니다.

Image Registration – Step 2) Estimating Geometric Transform
◆ (x', y') & (x, y)를 각각 입력 이미지와 참조 이미지의 기준점 좌표라고 합니다.
◆ Affine approximation (6-parameter model):
⚫ 두 이미지 모두에 3쌍의 기준점이 있는 경우 6개의 알려지지 않은 계수를 해결할 수 있습니다.
◆ Bilinear approximation (8-parameter model):
⚫ 두 이미지 모두에 4쌍의 기준점이 있으면 8개의 알려지지 않은 계수를 풀 수 있습니다.

Image Registration – Step 3) Intensity Interpolation

Image Registration – When the Results is Unsatisfactory..
◆ 보다 복잡한 모델 채택
⚫ 사변형보다 더 복잡한 영역을 사용하고 최소 제곱 알고리즘으로 피팅된 다항식과 같은 더 복잡한 모델을 사용하는 것이 가능합니다.
⚫ 문제를 해결하는 데 필요한 제어점의 수와 모델의 정교함은 기하학적 왜곡의 심각도에 따라 달라집니다.
◆ 또는 하위 이미지 기반 처리를 사용하세요.
1) 더 많은 수의 동점점을 선택합니다.
2) 4개의 연결점 그룹으로 형성된 사각형을 하위 이미지로 처리합니다.
3) 사변형 내의 모든 픽셀이 변환되면서 각 하위 이미지를 처리합니다.

Image Registration – Example
그림 2.42 이미지 등록.
(a) 참조 이미지.
(b) 입력(기하학적으로 왜곡된 이미지).
해당 동점은 모서리 근처에 작은 흰색 사각형으로 표시됩니다.
(c) 등록된(출력) 이미지(테두리의 오류 참고).
(d) (a)와 (c)의 차이점으로 더 많은 등록 오류가 표시됩니다.

- RANSAC
✓ 정의
✓ 동점(Key Point)
✓ 기하학적 변환 추정
✓ 결과가 만족스럽지 못한 경우

RANSAC (Radom Sample Consensus)
◆ 랜삭
⚫ 이상치가 포함된 관측 데이터 세트에서 수학적 모델의 매개변수를 추정하는 반복적 방법
⚫ 알고리즘 (일정 횟수 반복)
1. 원본 데이터의 무작위 하위 집합을 선택합니다. 이 부분 집합을 가상의 inliers라고 부릅니다.
2. 모델은 가상의 인라이어 세트에 맞춰집니다.
3. 일부 모델별 손실 함수에 따라 추정된 모델에 잘 맞는 (원본 데이터의) 모든 데이터 포인트를 합의 세트(즉, 모델의 인라이어 세트)라고 합니다.
4. 충분히 많은 데이터 포인트가 합의 세트의 일부로 분류된 경우 추정 모델은 상당히 양호합니다.
5. 합의 세트의 모든 구성원을 사용하여 모델을 재추정함으로써 모델을 개선할 수 있습니다.