
- 정현파
- 복소지수
- 정현파의 주파수 표현
- 정현파의 합
- 분석 및 합성
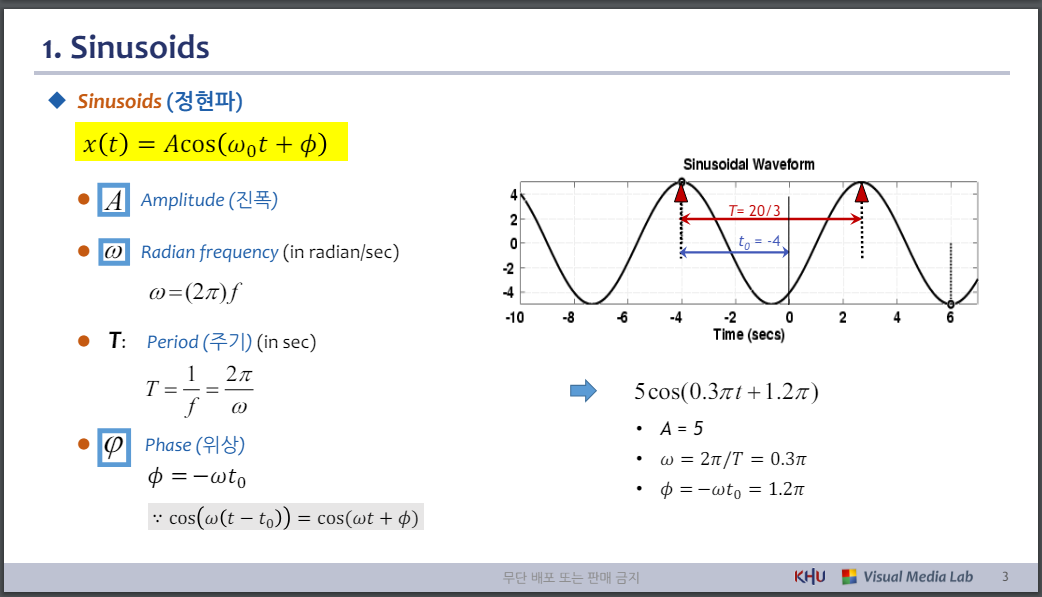
◆ Sinusoids (정현파)
⚫ Amplitude (진폭)
⚫ 라디안 주파수(라디안/초)
⚫ T: Period (주기) (in sec)
⚫ Phase (위상)

◆ 기본 삼각 항등식

◆ 복소수 표현
⚫ 직교형: z = x + jy
⚫ 극형: 𝒓∠𝜽
★ r : z의 크기(|z|)
★ q : z(인수 z)의 위상(인수)

⚫ Euler’s Formula:
⚫ Inverse Euler Formulas

◆ 복소지수
⚫ 이전 형식(예: 데카르트 및 극좌표)보다 더 나은 표현
⚫ 곱셈과 나눗셈에 좋습니다

◆ 정현파는 두 개의 복소 지수로 분해될 수 있습니다.
◆ 이를 주파수 표현 또는 신호의 주파수 스펙트럼이라고 합니다.


◆ Consider a complex exponential signal :

◆ 자연신호는 정현파의 합으로 표현될 수 있습니다.
◆ 따라서 복소수 지수의 합으로도 나타낼 수 있습니다.
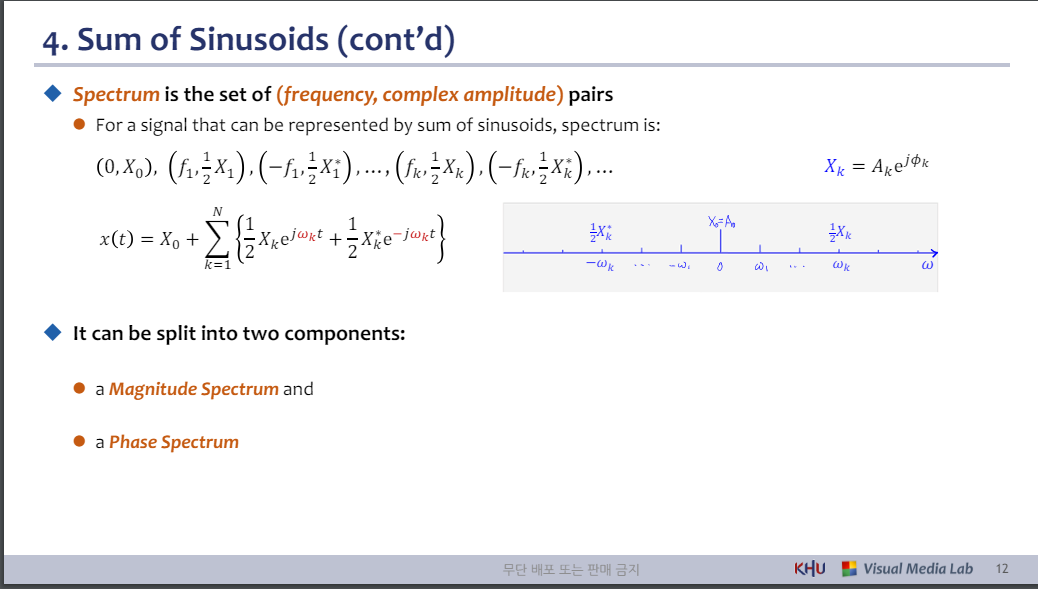
◆ 스펙트럼은 (주파수, 복소 진폭) 쌍의 집합입니다.
⚫ 정현파의 합으로 표현될 수 있는 신호의 경우 스펙트럼은 다음과 같습니다.
◆ 두 가지 구성 요소로 나눌 수 있습니다.
⚫ 크기 스펙트럼 및
⚫ 위상 스펙트럼

◆ 실제 신호의 공액 대칭
⚫ 공역대칭:
★ 각 음의 주파수 성분의 복소 진폭은 해당 양의 주파수 성분의 복소 진폭의 공액 복소수입니다.
⚫ 실수 신호 x(t)의 스펙트럼은 공액 대칭입니다.
★ 𝑓𝑘 및 −𝑓𝑘의 회전 페이저가 반대 방향으로 회전하고 결합하여 실제 신호를 형성
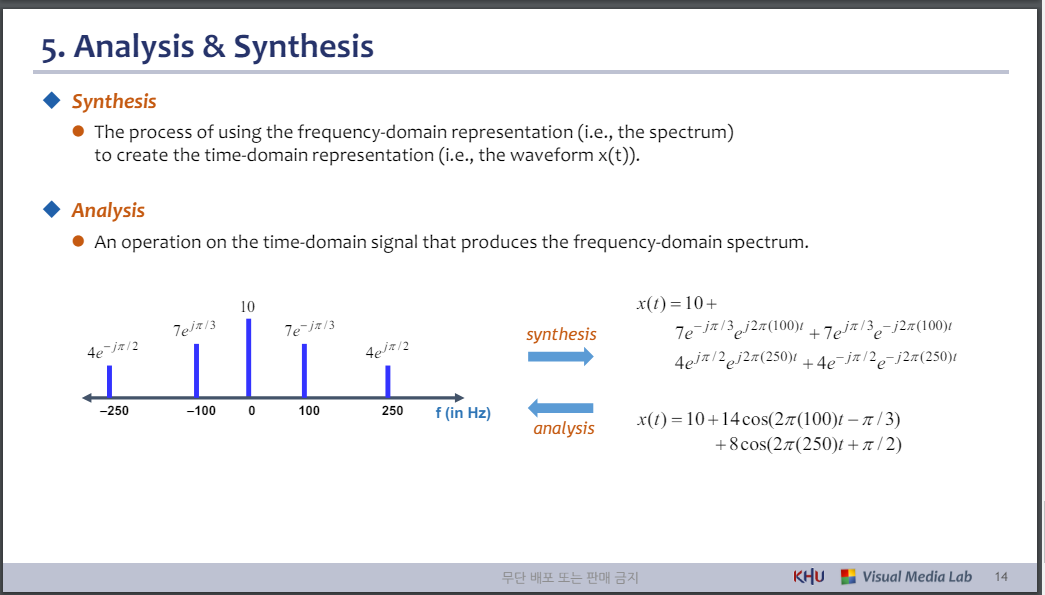
◆ 합성
⚫ 주파수 영역 표현(즉, 스펙트럼)을 사용하여 시간 영역 표현(즉, 파형 x(t))을 만드는 프로세스입니다.
◆ 분석
⚫ 주파수 영역 스펙트럼을 생성하는 시간 영역 신호에 대한 작업입니다.
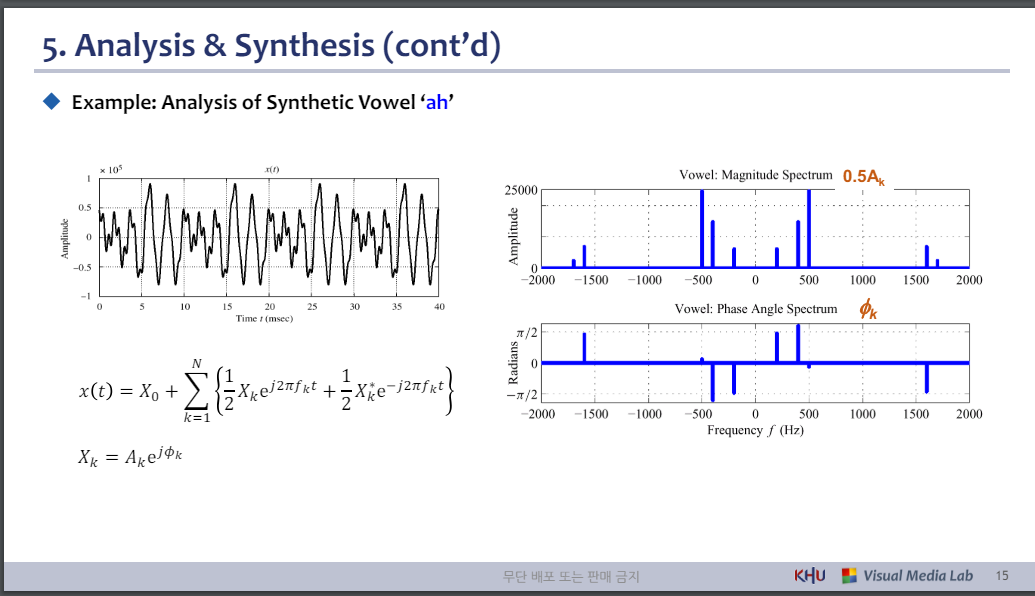
◆ 예시: 합성모음 '아' 분석