Lec.10b Fourier Transform & Sampling

1. 연속시간 푸리에 변환(CTFT)
▪ 연속시간 푸리에 급수
▪ 연속시간 푸리에 변환
▪ 2차원 푸리에 변환

2. 샘플링 및 재구성
   ▪ 이상적인 샘플링 및 재구성
   ▪ 섀넌 샘플링 정리
   ▪ 주파수 영역의 샘플링 및 재구성

1. 연속시간 푸리에 급수
2. 연속시간 푸리에 변환
3. 2차원 푸리에 변환

1. Continuous-Time Fourier Series

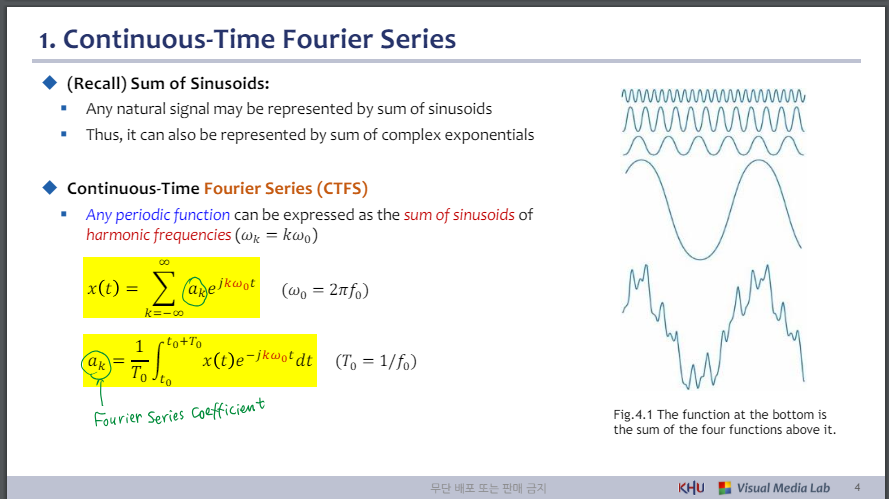
◆ (재현) 정현파의 합:
▪ 모든 자연 신호는 정현파의 합으로 표현될 수 있습니다.
▪ 따라서 복소수 지수의 합으로 나타낼 수도 있습니다.
◆ 연속시간 푸리에 급수(CTFS)
▪ 모든 주기 함수는 고조파 주파수의 정현파 합으로 표현될 수 있습니다(𝜔𝑘 = 𝑘𝜔0).

2. Continuous-Time Fourier Transform

◆ 연속시간 푸리에 변환(CTFT)
⚫ 주기적이지 않은 함수는 연속 주파수의 정현파 적분으로 표현될 수 있습니다.

3. 2-D Fourier Transform

2. Sampling & Reconstruction

1. 이상적인 샘플링 및 재구성
2. 섀넌 샘플링 정리
3. 주파수 영역에서의 샘플링 및 재구성
4. 샘플링이 충분하지 않습니까?

1. Sampling & Reconstruction

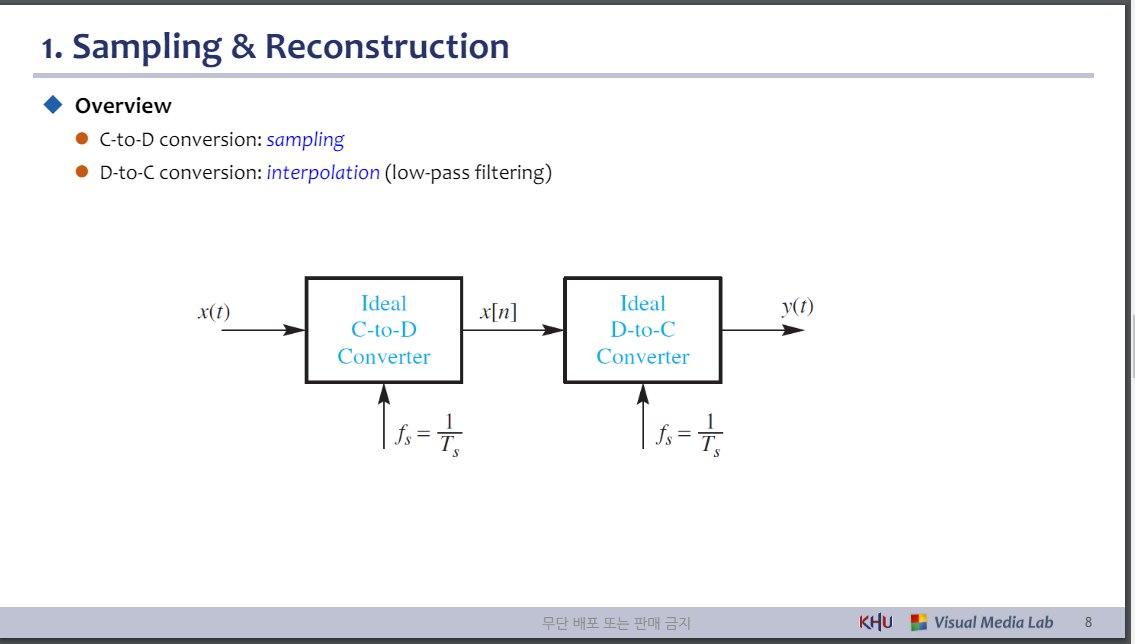
◆ 개요
⚫ C-to-D 변환: 샘플링
⚫ D-to-C 변환: 보간(저역 통과 필터링)

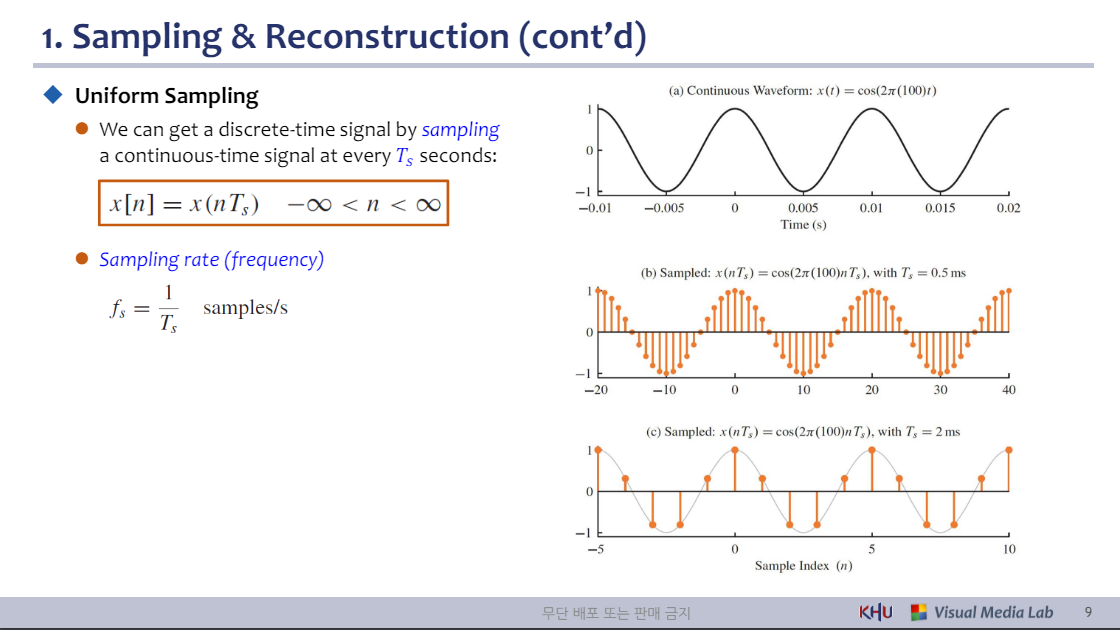
◆ 균일 샘플링
⚫ 매 𝑇𝑠초마다 연속시간 신호를 샘플링하여 이산시간 신호를 얻을 수 있습니다.
⚫ Sampling rate (frequency)

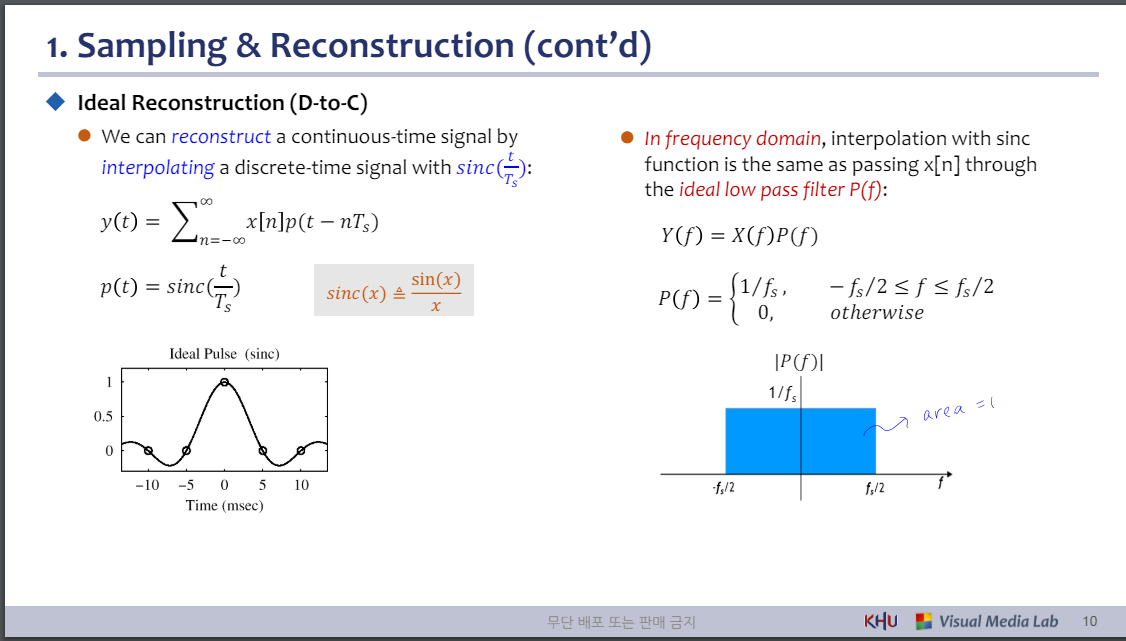
◆ 이상적인 재건(D-to-C)
⚫ 𝑠𝑖𝑛𝑐()를 사용하여 이산시간 신호를 보간하여 연속시간 신호를 재구성할 수 있습니다.

⚫ 주파수 영역에서 sinc 함수를 사용한 보간은 이상적인 저역 통과 필터 P(f)를 통해 x[n]을 전달하는 것과 동일합니다.

2. Shannon Sampling Theorem

2fmax의 최소 샘플링 속도를 나이퀴스트 속도라고 합니다.
⚫ 예 1: 오디오 CD 샘플링 속도는 44.1kHz입니다(가청 사운드 < 20kHz).
⚫ 예 2: 정현파 → 주기당 2개 이상의 샘플이 필요합니다.

3. Sampling & Reconstruction in Frequency Domain
   ◆ FT of Sampled Signal

그림 4.6
(a) 대역 제한 함수의 푸리에 변환에 대한 예시적인 스케치.
(b)–(d) 각각 오버샘플링, 비판적 샘플링 및 언더샘플링 조건에서 해당 샘플링된 함수를 변환합니다.

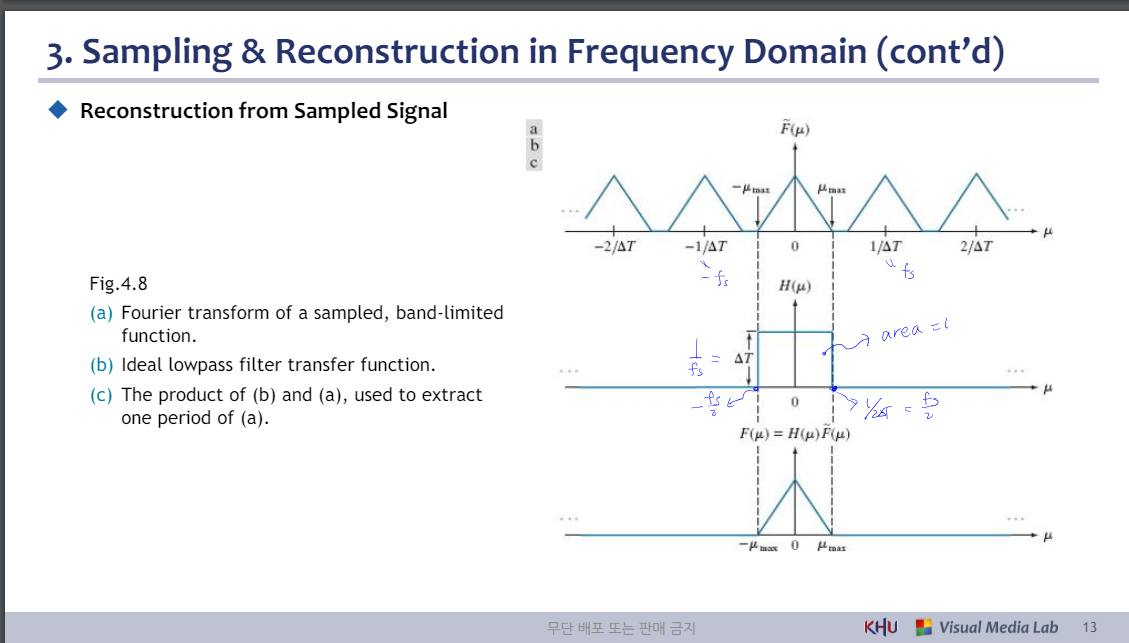
◆ Reconstruction from Sampled Signal
그림 4.8
(a) 샘플링된 대역 제한 함수의 푸리에 변환.
(b) 이상적인 저역통과 필터 전달 함수.
(c) (a)의 한 기간을 추출하는 데 사용되는 (b)와 (a)의 곱입니다.

4. Not Enough Sampling?

⚫ 샘플링 속도가 충분하지 않습니까?
★ 이런 일이 발생하면 완벽한 재구성이 어렵거나 불가능해집니다.
▪ 앨리어싱이 발생할 수 있습니다!

★ 앨리어싱을 방지하려면:
예를 들어 저역통과 필터를 사용하여 입력 신호 대역폭을 𝑓𝑠Τ2보다 작게 만듭니다.