1. 디지털 이미지를 위한 2차원 DFT
2. 주파수 영역 필터링
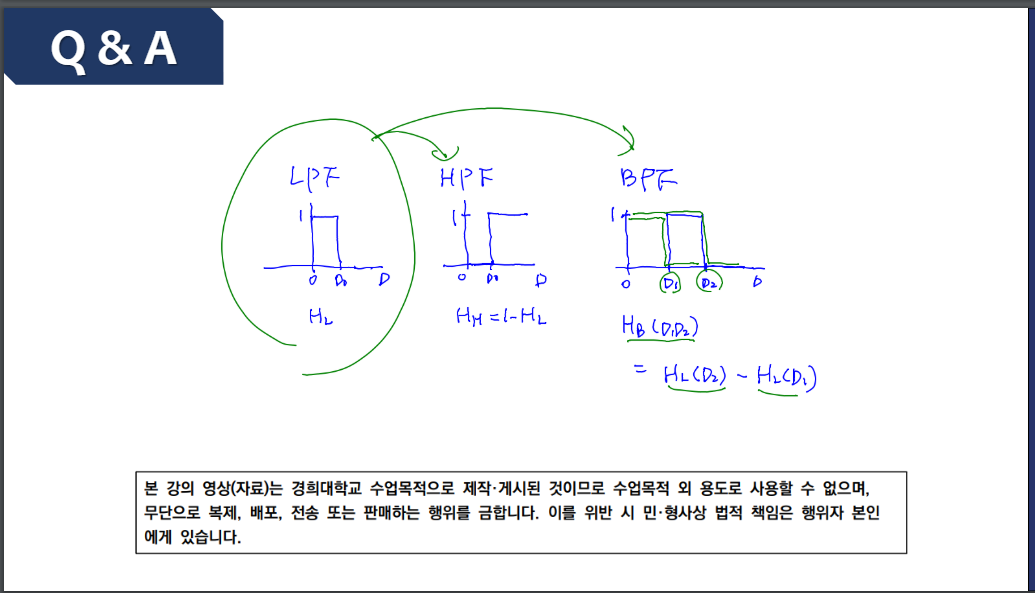
▪ 주파수 영역 필터링(T4.7)
▪ 저역통과 주파수 영역 필터(T4.8)
▪ 고역 주파수 도메인 필터(T4.9)

✓ 정의
✓ 주기성
✓ 크기 및 위상
✓ DC 구성요소
✓ 번역 및 회전
✓ 센터링
✓ 예시
✓ 속성 및 쌍 요약

2-D DFT for Digital Images – Definition
◆ 2-D DFT
• 때로는 문헌에서 IDFT 대신 DFT 앞에 1/MN 상수가 있는 것을 발견할 수 있습니다.
• 때때로 이 상수의 제곱근이 정변환 및 역변환 앞에 포함되어 보다 대칭적인 쌍을 생성합니다.
• 일관되게 사용된다면 이러한 공식은 모두 정확합니다.
디지털 이미지를 위한 2차원 DFT – 주기성
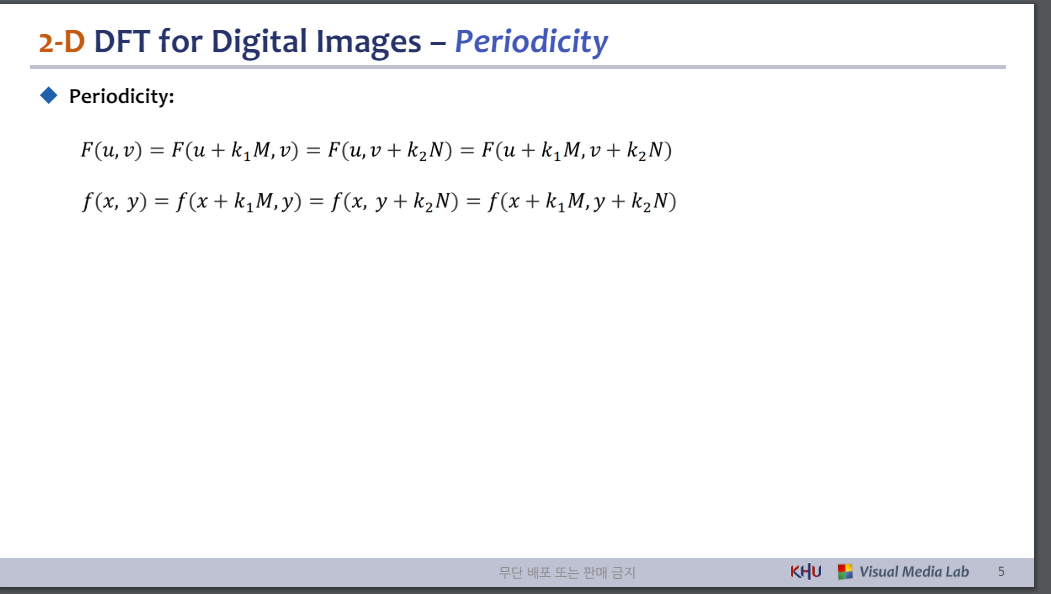
◆ Periodicity:

디지털 이미지를 위한 2D DFT – 크기 및 위상
◆ 크기 및 위상각
▪ 크기 및 위상
▪ 전력 스펙트럼 밀도(PSD)
◆ 실제 신호의 경우
디지털 이미지를 위한 2차원 DFT - DC 구성요소
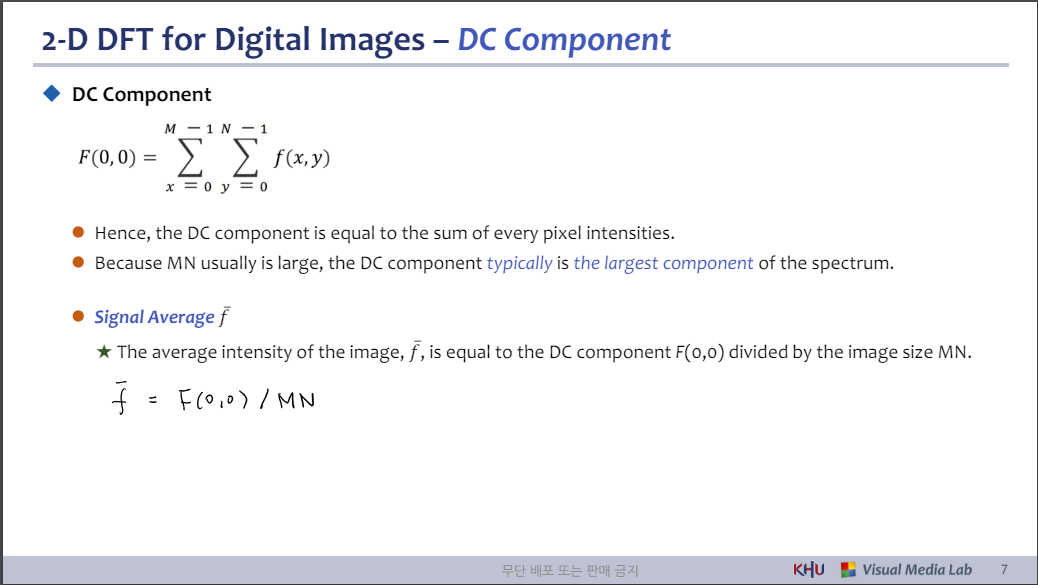
◆ DC Component
⚫ 따라서 DC 성분은 모든 픽셀 강도의 합과 같습니다.
⚫ MN은 일반적으로 크기 때문에 DC 구성 요소는 일반적으로 스펙트럼의 가장 큰 구성 요소입니다.
⚫ 신호 평균 𝑓ҧ
★ 이미지의 평균 강도 𝑓ҧ는 DC 구성 요소 F(0,0)를 이미지 크기 MN으로 나눈 값과 같습니다.

디지털 이미지를 위한 2차원 DFT - 변환 및 회전
◆ Translation
◆ Rotation

2-D DFT for Digital Images – Centering
◆ 스펙트럼 중심 맞추기
그림 4.22 푸리에 변환을 중심에 두기.
(a) 무한한 수의 기간을 보여주는 1차원 DFT.
(b) F(u)를 계산하기 전에 f(x)에 (-1)x를 곱하여 얻은 이동된 DFT.
(c) 무한한 수의 기간을 보여주는 2차원 DFT. 점선 직사각형 내의 영역은 Eq.로 얻은 데이터 배열 F(u,v)입니다. (4-67) 이미지 f(x,y)를 입력으로 사용합니다. 이 배열은 4개의 분기 기간으로 구성됩니다. (d) F(u,v)를 계산하기 전에 f(x,y)에 (-1)x+y를 곱하여 얻은 이동된 배열. 이제 데이터에는 (b)와 같이 하나의 완전한 중앙 집중 기간이 포함됩니다.
2-D DFT for Digital Images – Example (Centering)
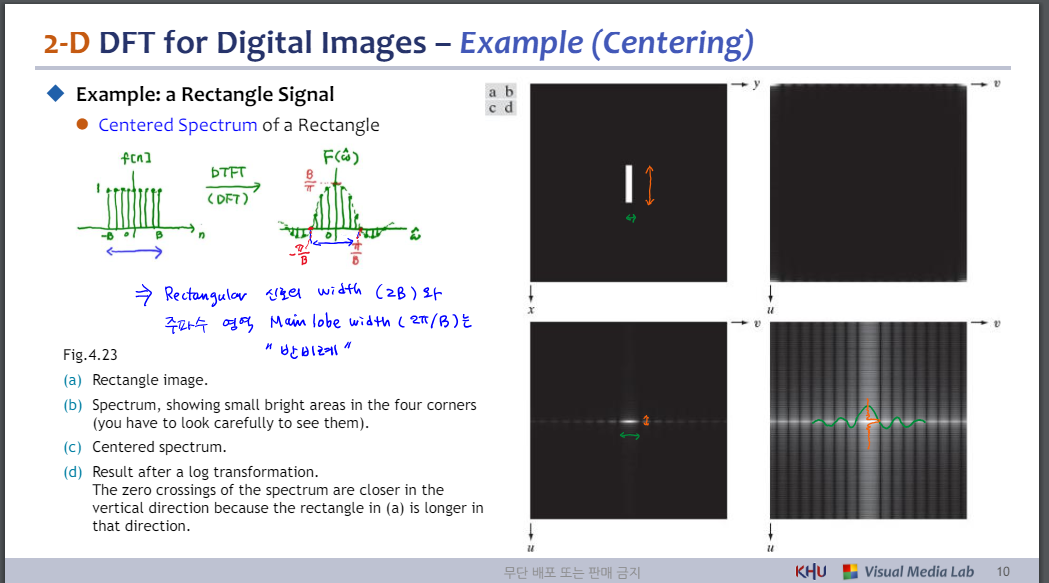
◆ 예: 직사각형 신호
⚫ 직사각형의 중심 스펙트럼
그림 4.23
(a) 직사각형 이미지.
(b) 스펙트럼, 네 모서리에 작고 밝은 영역이 표시됩니다(보려면 주의 깊게 관찰해야 합니다).
(c) 중심 스펙트럼.
(d) 로그 변환 후의 결과. (a)의 직사각형이 수직 방향으로 더 길기 때문에 스펙트럼의 영점 교차점은 수직 방향으로 더 가깝습니다.

2-D DFT for Digital Images – Example (Translation & Rotation)
◆ Example: a Rectangle Signal (cont’d)
⚫ Translation & Rotation
그림 4.24
(a) 그림 4.23(a)의 직사각형이 번역되었습니다. 변환된 직사각형의 스펙트럼은 그림 4.23(a)의 원본 이미지 스펙트럼과 동일합니다.
(b) 해당 스펙트럼.
(c) 회전된 직사각형.
(d) 해당 스펙트럼.

2-D DFT for Digital Images – Properties Summary
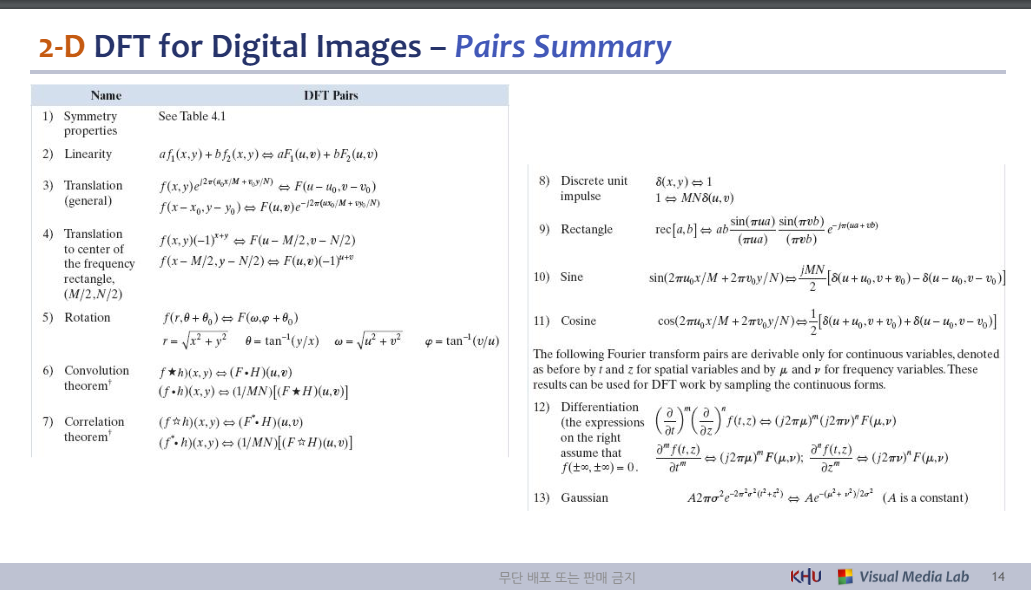
2-D DFT for Digital Images – Pairs Summary

-
Frequency Domain Filtering
-
주파수 영역 필터링(T4.7)
-
저역통과 주파수 영역 필터(T4.8)
-
고역 주파수 영역 필터(T4.9)

1. 주파수 영역 필터링 – 직관
◆ 직관: 크기 스펙트럼
⚫ 크기 스펙트럼은 스펙트럼이 생성된 이미지의 총 강도 특성에 대한 몇 가지 유용한 지침을 제공합니다.
그림 4.28 (a) 손상된 집적 회로의 SEM 이미지. (b) (a)의 푸리에 스펙트럼.

◆ 직관: 주파수 영역 필터링
그림 2.45
(a) 정현파 간섭으로 인해 이미지가 손상되었습니다.
(b) 간섭으로 인한 에너지 폭발을 보여주는 푸리에 변환의 크기.
(c) 에너지 폭발을 제거하는 데 사용되는 마스크.
(d) 수정된 푸리에 변환의 역을 계산한 결과.
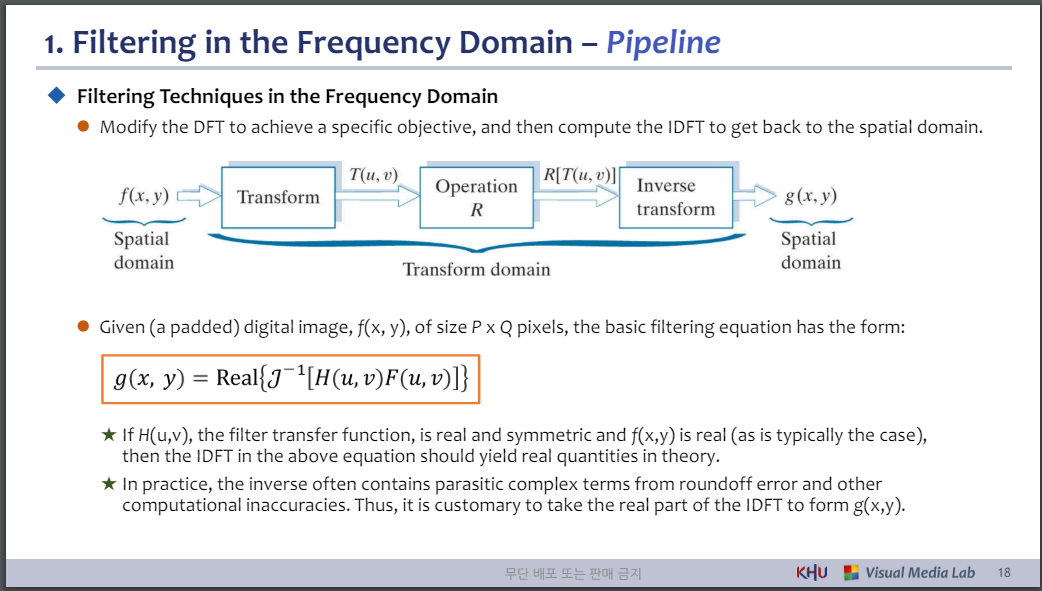
1. 주파수 영역 필터링 - 파이프라인
◆ 주파수 영역의 필터링 기법
⚫ 특정 목표를 달성하기 위해 DFT를 수정한 다음 IDFT를 계산하여 공간 영역으로 돌아갑니다.
⚫ P x Q 픽셀 크기의 (패딩된) 디지털 이미지 f(x, y)가 주어지면 기본 필터링 방정식의 형식은 다음과 같습니다.
★필터 전달 함수인 H(u,v)가 실수이고 대칭이고 f(x,y)가 실수(일반적인 경우)인 경우 위 방정식의 IDFT는 이론상 실수를 산출해야 합니다.
★실제로 역함수에는 반올림 오류 및 기타 계산 부정확성으로 인한 기생 복소 항이 포함되는 경우가 많습니다. 따라서 IDFT의 실수 부분을 취하여 g(x,y)를 형성하는 것이 일반적입니다.

- Filtering in the Frequency Domain – Zero Padding
◆ 2차원 이산 컨벌루션 정리
⚫ 2차원 원형 컨볼루션
⚫ Fourier Transform
⚫ 순환 컨볼루션에는 제로 패딩이 필요합니다
그림 4.27
왼쪽 열: 공간 컨볼루션
오른쪽 열: 원형 컨볼루션.
(j)의 실선은 DFT를 사용하여 얻을 수 있는 결과입니다.
이 잘못된 결과는 제로 패딩을 사용하여 해결할 수 있습니다.

- Filtering in the Frequency Domain – Algorithm
◆ 주파수 영역 필터링 단계
M x N 크기의 입력 이미지 f(x, y)가 주어지면:
① [Padding] 제로 패딩, 미러 패딩, 복제 패딩을 이용하여 P x Q (P=2M, Q=2N) 크기의 패딩된 이미지 fp (x, y)를 형성합니다.
② [중앙화] fp(x, y)에 (−1)(𝑥+𝑦)을 곱하여 DFT를 P x Q 주파수 직사각형의 중앙에 배치합니다.
③ [DFT] 2단계 이미지의 DFT F(u, v)를 계산합니다.
④ [필터링] 요소별 곱셈을 이용하여 G(u, v)= H(u, v)F(u, v)의 곱을 만든다.
▪ H(u, v)는 (P/2,Q/2)에 중심이 있는 P x Q 크기의 실수 대칭 필터여야 합니다.
⑤ [IDFT] G(u,v)의 IDFT를 계산하여 필터링된 이미지 gp(x,y)(크기 P x Q)를 얻습니다.
⑥ [추출] gp(x, y)의 왼쪽 상단 사분면 영역을 추출하여 입력 영상과 동일한 크기의 최종 필터링 결과 g(x, y)를 구합니다.

그림 4.35
(a) M X N 이미지, f.
(b) 패딩된 이미지, 크기 P X Q의 fp.
(c) fp에 (-1)x+y를 곱한 결과.
(d) F의 스펙트럼.
(e) P X Q 크기의 중심 가우스 저역 통과 필터 전달 함수 H.
(f) 생성물 HF의 스펙트럼에 (-1)x+y를 곱합니다.
(g) gp의 처음 M행과 N열을 추출하여 얻은 최종 결과 g.
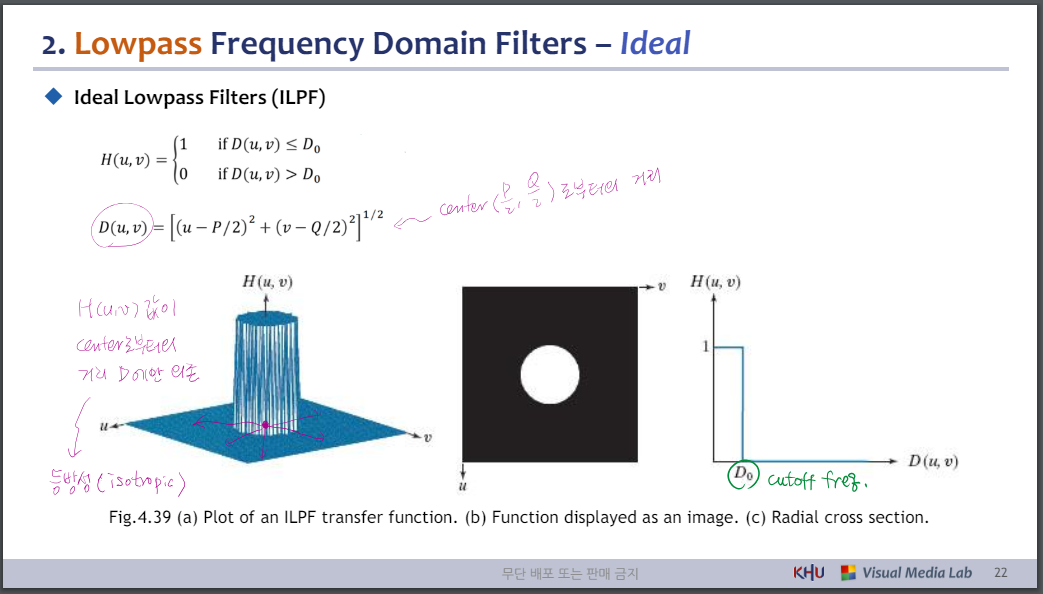
- 저역 통과 주파수 도메인 필터 - 이상적
◆ Ideal Lowpass Filters (ILPF)
그림 4.39 (a) ILPF 전달 함수의 플롯. (b) 이미지로 표시되는 기능입니다. (c) 방사형 단면.

◆ ILPF의 공간 커널
그림 4.42 (a) 주파수 영역 ILPF 전달 함수. (b) 해당 공간 도메인 커널 기능.
(c) (b)의 중심을 통과하는 수평선의 강도 프로파일.
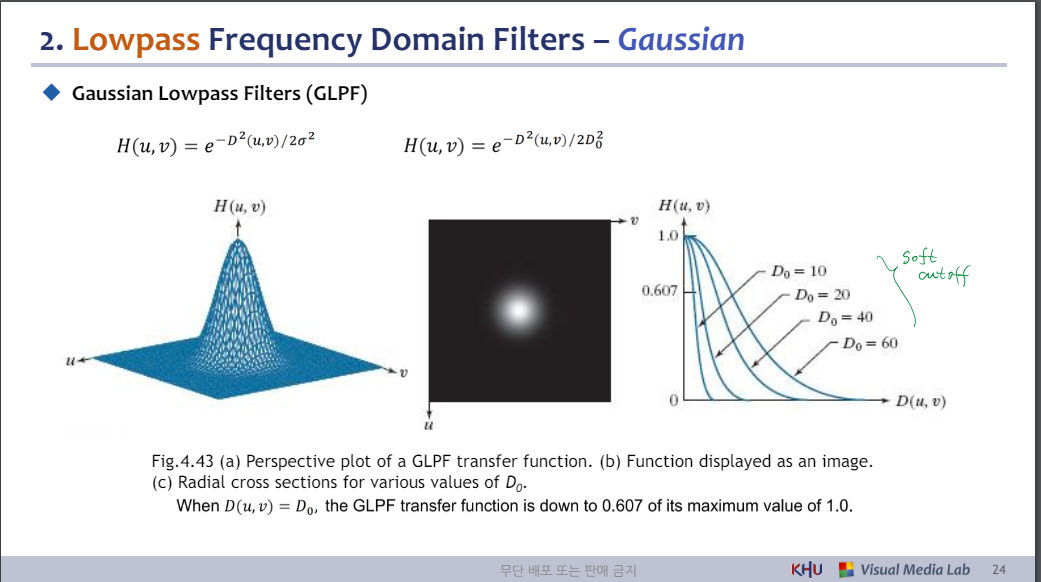
◆ Gaussian Lowpass Filters (GLPF)
그림 4.43 (a) GLPF 전달 함수의 투시도. (b) 이미지로 표시되는 기능입니다.
(c) 다양한 D0 값에 대한 방사형 단면

◆ Examples: GLPF
그림 4.44
(a) 크기 688 X 688 픽셀의 원본 이미지.
(b)-(f) 반경 10, 30, 60, 160 및 460 픽셀에서 차단 주파수를 갖는 GLPF를 사용한 필터링 결과.
제로 패딩의 특징인 검은색 테두리를 피하기 위해 미러 패딩을 사용했습니다.
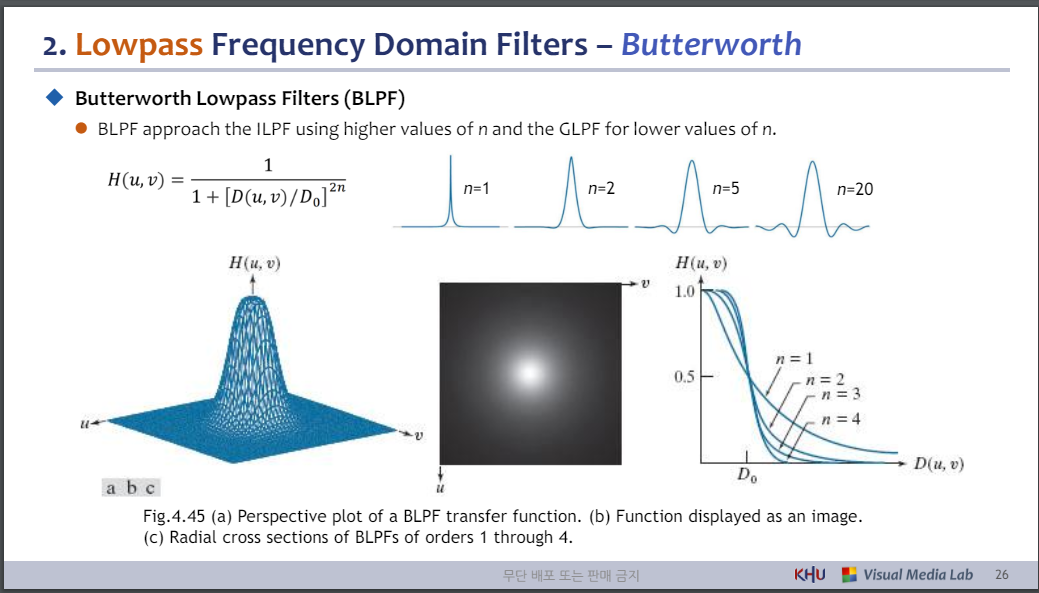
- 저역 통과 주파수 영역 필터 – 버터워스
◆ 버터워스 저역통과 필터(BLPF)
⚫ BLPF는 더 높은 n 값을 사용하고 GLPF를 더 낮은 n 값에 사용하여 ILPF에 접근합니다.
그림 4.45 (a) BLPF 전달 함수의 투시도. (b) 이미지로 표시되는 기능입니다.
(c) 1~4차 BLPF의 방사형 단면.

- 저역통과 주파수 영역 필터 - 비교
◆ ILPF, GLPF, BLPF 비교(n=2.25) 결과
⚫ 세 가지 필터 모두의 차단 주파수는 160픽셀로 설정되어 있습니다.
⚫ 첫 번째 이미지에서 ILPF의 출력인 '울리는 아티팩트'를 관찰하세요.
링잉 아티팩트의 주요 원인은 신호가 대역 제한되거나 저역 통과 필터를 통과하기 때문입니다.
시간 영역 측면에서 이러한 유형의 링잉의 원인은 ILPF의 임펄스 응답인 sinc 함수의 잔물결입니다. 수학적으로 이를 깁스 현상이라고 합니다.
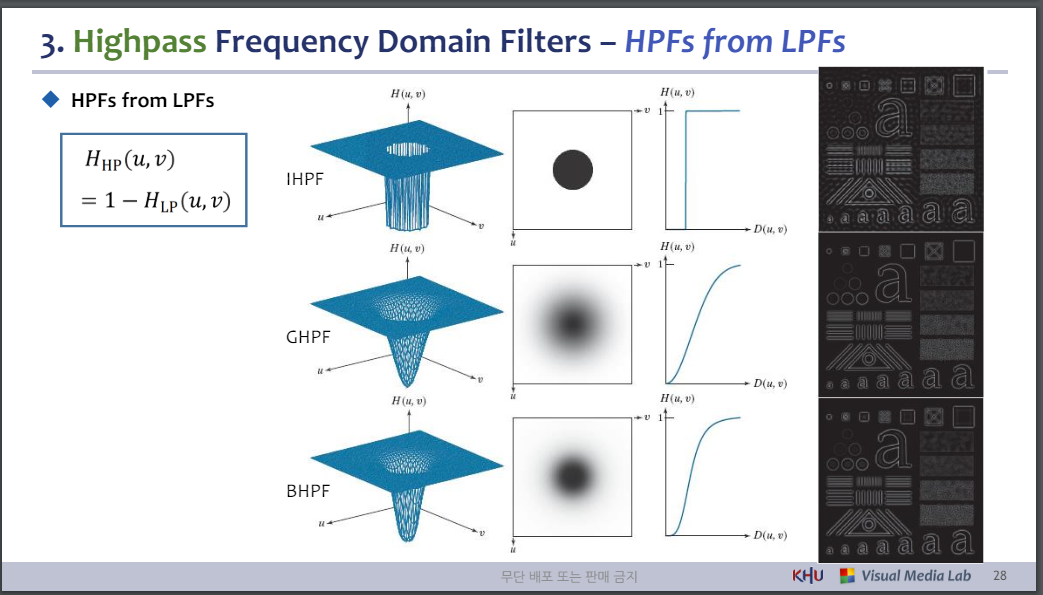
3. 고역 통과 주파수 도메인 필터 - LPF의 HPF
◆ HPFs from LPFs

- 고역 통과 주파수 도메인 필터 - 이미지 샤프닝
◆ HPF를 이용한 이미지 샤프닝
⚫ 언샵 마스킹 불러오기 (강의 04)
⚫ Unsharp mask로 HPF된 입력신호를 사용하면 Sharpening 된 영상을 얻을 수 있음