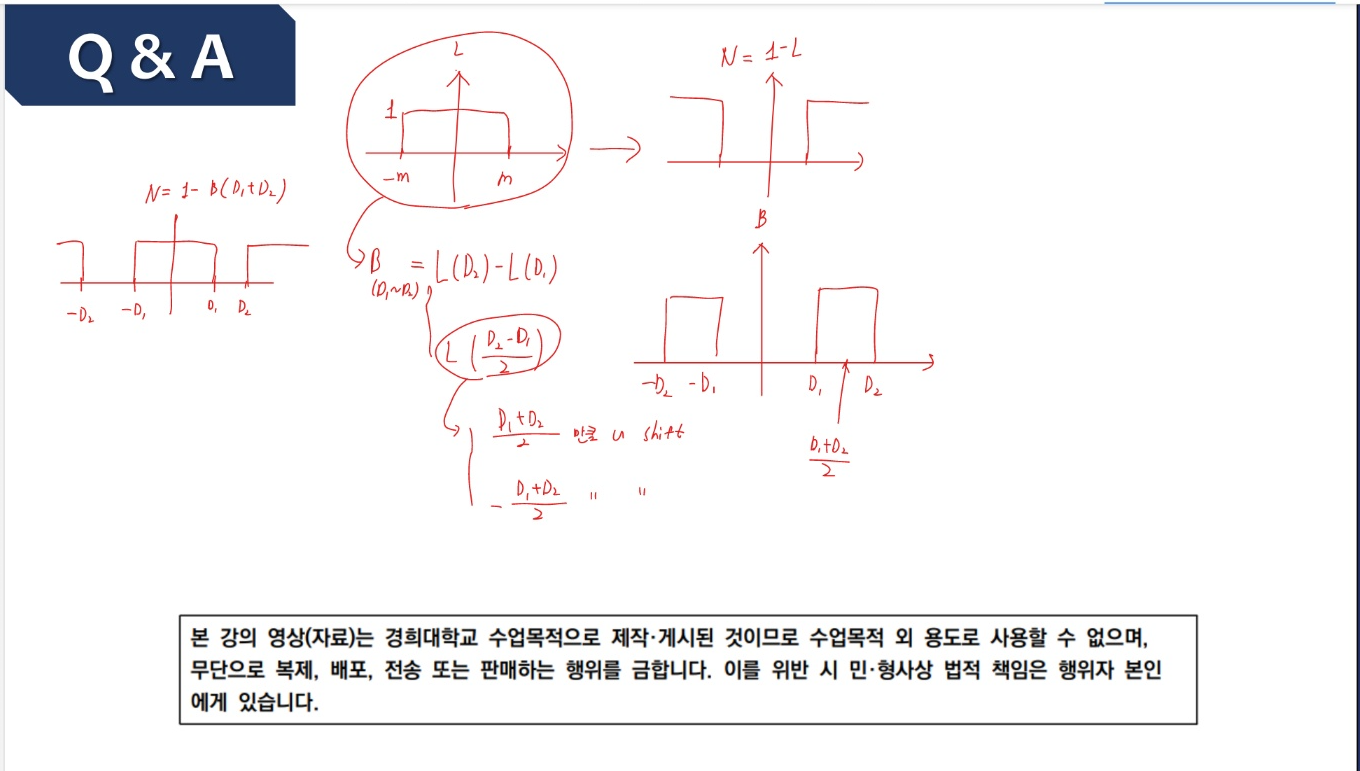
❹ 1부. (검토) 1-D LTI 시스템
❹ 2부. 공간 도메인 필터링(T3.4~3.6, T10.2)
❹ 3부. 이미지 노이즈 제거(T5.1~5.3)

Part III. Image Denoising
1. 영상 저하 및 복원 모델(T5.1)
2. 잡음 모델(T5.2)
3. 잡음 매개변수 추정(T5.2)
4. 공간 필터링을 사용한 노이즈 제거(T5.3)
5. 노치 필터링을 이용한 주기적인 노이즈 감소
1. Image Degradation & Restoration Model
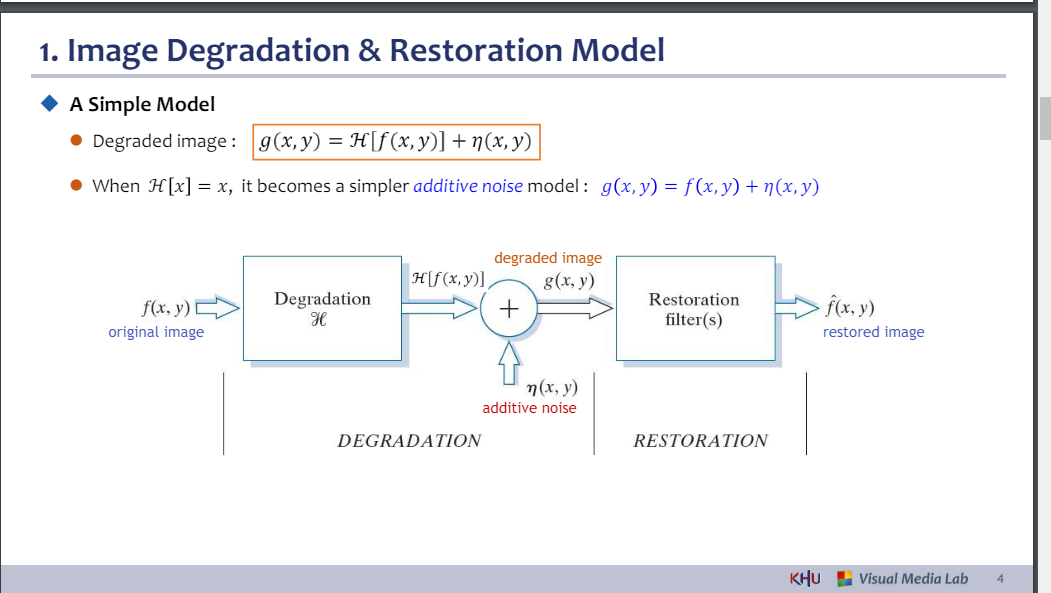
◆ 간단한 모델
⚫ 저하된 이미지 :
⚫ ℋ 𝑥 = 𝑥이면 더 간단한 추가 노이즈 모델이 됩니다.

- Noise Models
◆ 소음원
⚫ 디지털 이미지의 주요 노이즈 원인은 이미지 획득 및/또는 전송 중에 발생합니다.
★ CCD 카메라로 이미지를 획득할 때 조도와 센서 온도는 결과 이미지의 노이즈 양에 영향을 미치는 주요 요소입니다.
★ 무선 네트워크를 사용하여 전송된 이미지는 번개나 기타 대기 장애로 인해 손상될 수 있습니다.
⚫ 공간적으로 주기적인 노이즈를 제외하고,
1) 소음은 공간 좌표와 무관합니다.
2) 노이즈는 이미지 자체와 관련이 없습니다.
(즉, 픽셀 값과 노이즈 성분 값 사이에는 상관관계가 없습니다.)
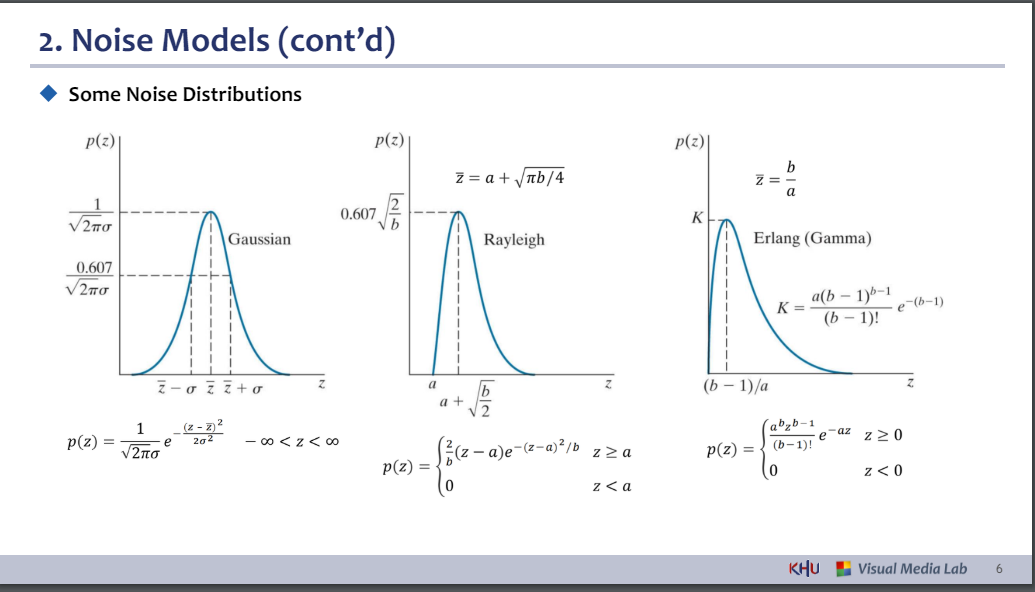
◆ Some Noise Distributions

◆ Some Noise Distributions (cont’d)

◆ 소음 부패 상황의 예
⚫ 가우시안 노이즈는 조명 불량이나 고온으로 인한 전자 회로 노이즈, 센서 노이즈 등의 요인으로 인해 이미지에 발생합니다.
⚫ 레일리 밀도는 범위 이미징에서 노이즈 현상을 특성화하는 데 도움이 됩니다.
⚫ 지수 밀도와 감마 밀도는 레이저 이미징에 적용됩니다.
⚫ 임펄스 노이즈는 이미징 중에 잘못된 스위칭과 같은 빠른 과도 현상이 발생하는 상황에서 발견됩니다.
⚫ 균일한 밀도는 아마도 실제 상황을 가장 잘 설명하지 못할 것입니다.
★ 그러나 균일한 밀도는 시뮬레이션에서 광범위하게 사용되는 수많은 난수 생성기의 기초로 매우 유용합니다.
★ 균일한 양자화 프로세스는 원래 신호에 균일한 노이즈를 추가하는 것으로 모델링될 수 있습니다.
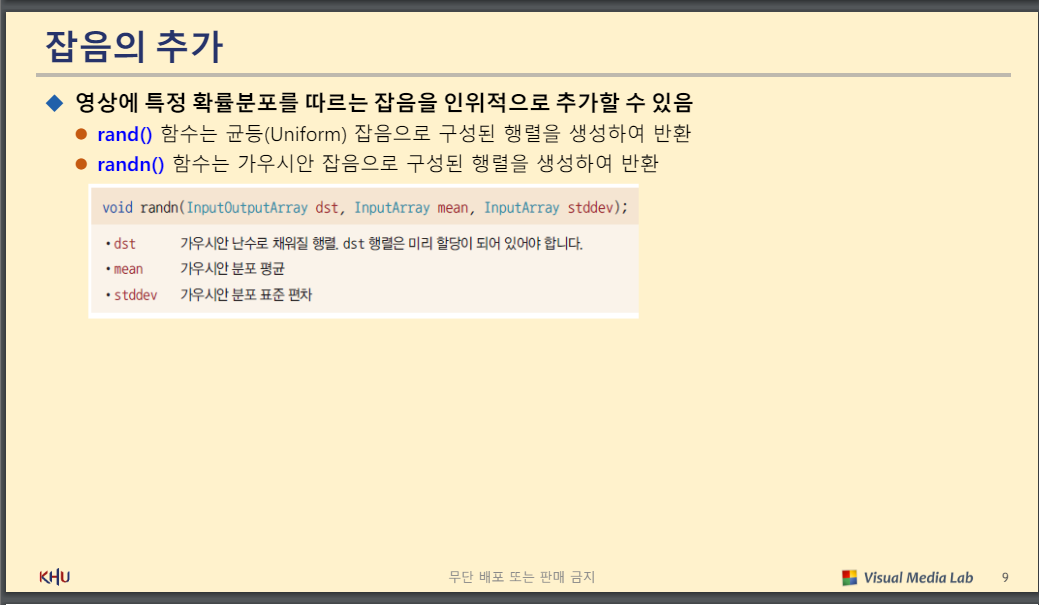
잡음의 추가

◆ 어떤 유형의 소음이 발생합니까?
⚫ 노이즈가 있는 이미지의 히스토그램을 검사합니다(노이즈가 없는(실측) 버전에 대해 알 수 있다고 가정)

◆ 주기적 노이즈 → 푸리에 스펙트럼 조사
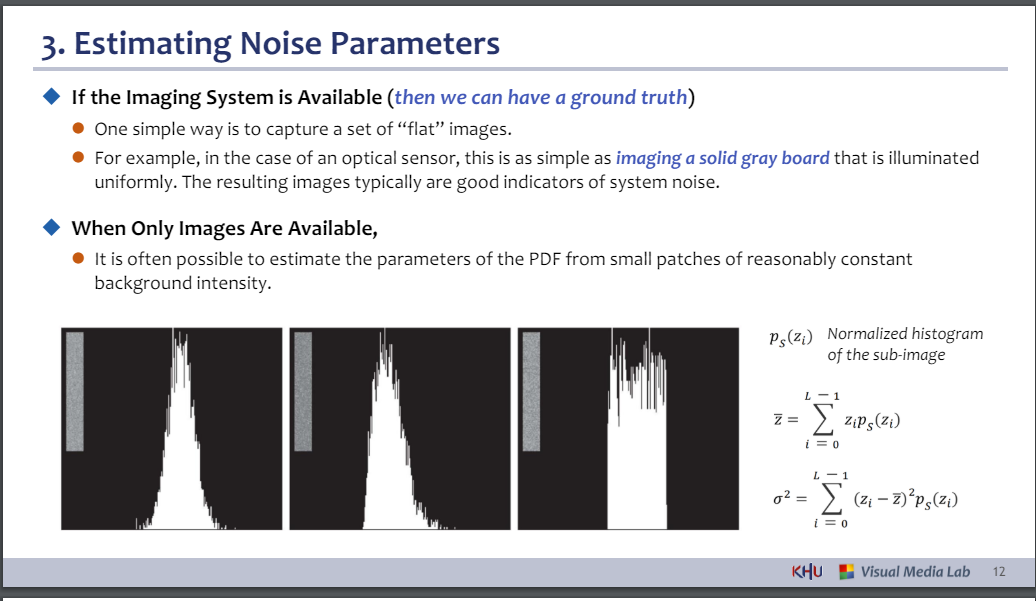
- Estimating Noise Parameters
◆ 이미징 시스템을 사용할 수 있는 경우(실측 정보를 얻을 수 있음)
⚫ 간단한 방법 중 하나는 "평평한" 이미지 세트를 캡처하는 것입니다.
⚫ 예를 들어 광학 센서의 경우 균일하게 조명되는 단단한 회색 보드를 이미징하는 것만 큼 간단합니다. 결과 이미지는 일반적으로 시스템 노이즈를 나타내는 좋은 지표입니다.
◆ 이미지만 사용할 수 있는 경우,
⚫ 합리적으로 일정한 배경 강도의 작은 패치에서 PDF의 매개변수를 추정하는 것이 가능한 경우가 많습니다.
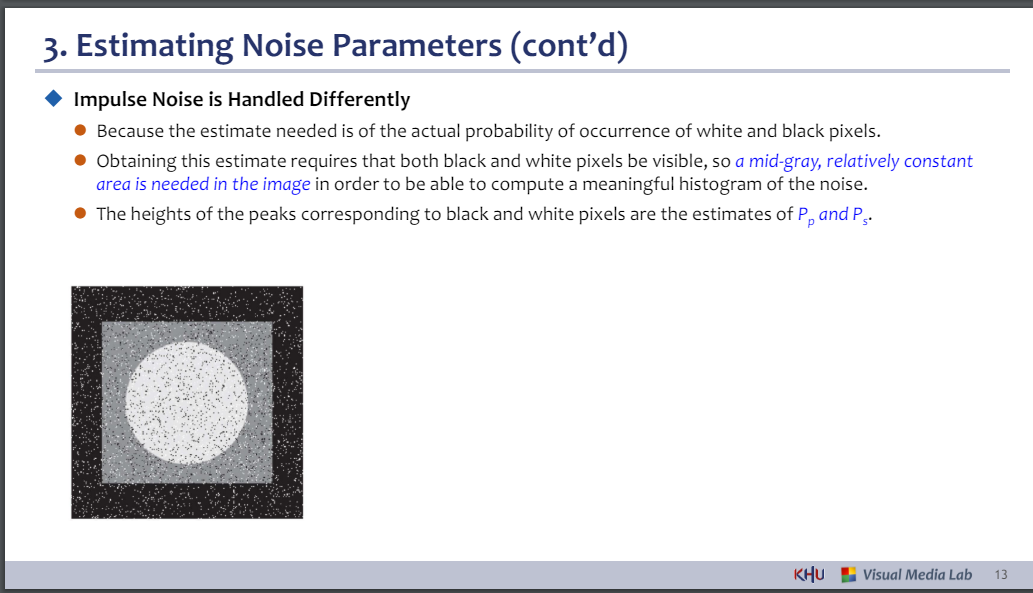
◆ 임펄스 노이즈는 다르게 처리됩니다.
⚫ 필요한 추정치는 흰색과 검은색 픽셀이 발생할 실제 확률이기 때문입니다.
⚫ 이 추정값을 얻으려면 검은색과 흰색 픽셀이 모두 표시되어야 하므로 의미 있는 노이즈 히스토그램을 계산하려면 이미지에 중간 회색의 비교적 일정한 영역이 필요합니다.
⚫ 흑백 픽셀에 해당하는 피크의 높이는 Pp 및 Ps의 추정치입니다.
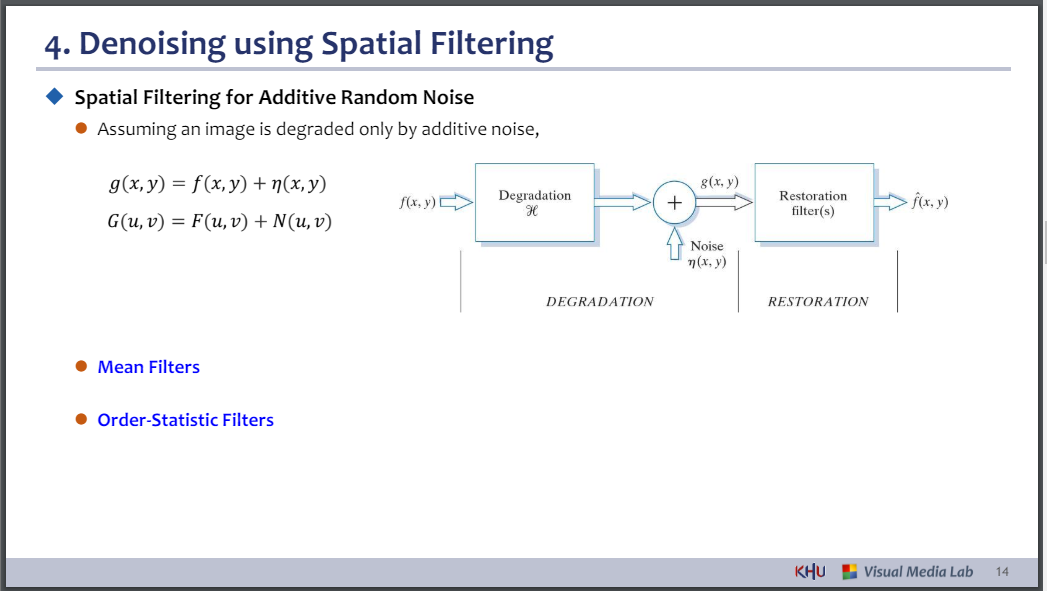
- Denoising using Spatial Filtering
◆ 추가 랜덤 노이즈에 대한 공간 필터링
⚫ 이미지가 부가적인 노이즈에 의해서만 저하된다고 가정하면,
⚫ 평균 필터
⚫ 주문 통계 필터

◆ Mean Filters
⚫ (Arithmetic) Mean Filter ⚫ Geometric Mean Filter
⚫ Harmonic Mean Filter ⚫ Contraharmonic Mean Filter
Q > 0은 후추 소음을 제거합니다.
Q < 0은 솔트 노이즈를 제거합니다.
반고조파 필터는 Q = 0이면 산술 평균 필터로 감소하고 Q = -1이면 고조파 평균 필터로 감소합니다.



- Denoising using Spatial Filtering (cont’d)

◆ Order-Statistic Filters
⚫ Median Filter ⚫ Max & Min Filters
⚫ Midpoint Filter ⚫ Alpha-Trimmed Mean Filter
d의 범위는 0에서 mn-1까지일 수 있습니다.
d = 0일 때 알파 트리밍 필터는 산술 평균 필터로 축소됩니다.
d = mn-1을 선택하면 필터는 중앙값 필터가 됩니다.

4. Denoising using Spatial Filtering (cont’d)

4. Denoising using Spatial Filtering (cont’d)

5. Periodic Noise Reduction Using Notch Filtering
◆ 주기적인 소음
⚫ 주기적인 노이즈의 매개변수는 일반적으로 푸리에 스펙트럼을 검사하여 추정됩니다.
★ 주기적인 노이즈는 시각적 분석으로도 종종 감지할 수 있는 주파수 스파이크를 생성하는 경향이 있습니다.
⚫ 또 다른 접근 방식은 이미지에서 직접 노이즈 성분의 주기성을 추론하는 것이지만 이는 단순한 경우에만 가능합니다.