이번 포스터에서 알아볼 내용은 두 개의 이미지 간에 호모그래피 행렬을 계산하는 개념과 유효하지 않은 매치를 구분하는 어려움에 대한 것 입니다.
이러한 문제를 해결하기 위해 RANSAC (랜덤 샘플 일치) 알고리즘을 소개하고 그 일반적인 작동 원리를 설명하겠습니다. 또한 RANSAC를 사용하여 Line fitting의 예시와 함께 그 효과를 알아보겠습니다.
Q. RANSAC을 사용하는 이유?
Computer Vision에서 두 이미지 사이의 Homography matrix를 계산할 때, 일치하는 특징을 사용하게 됩니다. 하지만 이렇게 찾아낸 특징 pair들이 실질적으로 같은 지는 확신할 수 없습니다. 겉보기에 같아 보여도 3D에서 나온 것이기에 확신은 불가합니다. 즉, 동일한 3D지점에서의 투영인지를 모르기에, 모든 일치하는 특징들을 찾아내는 데에는 한계가 존재합니다.
=> 따라서 이렇게 유효하지 않은 것을 걸러내고 정확한 Homography matrix를 계산하기 위해 나온 것이 RANSAC:random sample consensus입니다!
아래와 같이 matching을 시켰을 때, Outlier들을 찾아내는 것 입니다.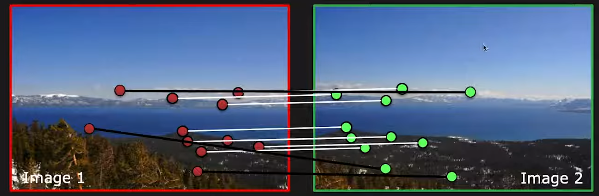
RANSAC는 1980년대 초기에 개발된 다목적 알고리즘으로, 이상치를 포함하는 여러 문제에 적용할 수 있습니다. 이상치의 수가 전체 데이터의 50% 미만인 경우에 잘 작동합니다.
RANSAC의 핵심 단계는 다음과 같습니다.
1) 주어진 데이터 집합에서 최소한의 데이터 포인트 (s)를 무작위로 선택합니다. (주로 s=4)
2) 이러한 무작위 샘플을 사용하여 우리의 모델인 호모그래피 행렬을 만들어 냅니다.
3) 지정된 임계값 (epsilon) 내에서 모델에 맞는 전체 데이터 포인트 (M : inliers)의 수를 세어봅니다.
4) 이러한 1-3 단계를 N번 반복하며 매번 다른 무작위 샘플을 선택합니다.
5) 최종적으로 가장 많은 inliers(모델에 맞는 데이터 포인트)를 가진 모델(homography matrix)을 선택합니다.
++ 추가적으로 선택한 모델을 사용하여 예측 결과를 개선하고자 할 경우, 인라이어를 사용하여 모델을 재계산합니다.
Ransac Example
1) Line Fitting
RANSAC를 사용하여 데이터 집합이 주어지면 데이터에 선을 맞추는 것이 목표입니다. 전통적인 방법인 최소 제곱 맞춤을 사용한다면, 아래와 같은 그림은 이상치 때문에 부정확한 선이 나올 수 있습니다. 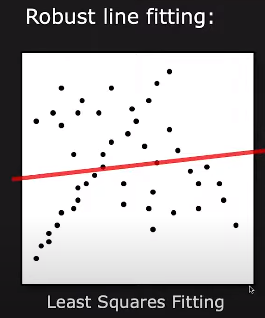
그러나 RANSAC는 반복적으로 무작위 점 쌍을 선택하고 동일한 클러스터에 속하는 인라이어를 식별합니다. 가장 많은 인라이어를 가진 모델을 선택함으로써 RANSAC는 이상치가 있는 상황에서도 올바른 선을 견고하게 추정할 수 있는 것 입니다.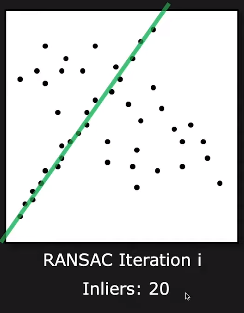
정리하자면, 기존 호모그래피 행렬 계산할 때, 유효하지 않은 일치를 선정하는데에 대한 어려움이 존재했었습니다. 이를 RANSAC 알고리즘을 사용하여 컴퓨터 비전 작업에서 이상치 문제를 효과적으로 해결한 것 입니다.
참고 : https://www.youtube.com/watch?v=EkYXjmiolBg&list=PL2zRqk16wsdp8KbDfHKvPYNGF2L-zQASc&index=5
