Homography는 Computer Vision 이미지 처리에서 중요한 역할을 하는 transformation matrix입니다. Homography는 주로 특정 projection지점을 통해 하나의 평면에서 다른 평면으로 점들을 매핑합니다. 이번 포스터에서는 이와 관련해서 계산하는 과정을 알아보겠습니다.
1. Image Stitching and Homography
이미지 스티칭은 파노라마와 같이 여러 이미지들을 결합하여 연속적이고 자연스럽게 만드는 과정입니다.
Q. 이를 달성하기 위해 Homography가 어떻게 작용될까요?
예를 들어 3D 세계에서 다양한 시점에서 이미지를 촬영하는 상황을 가정하겠습니다.
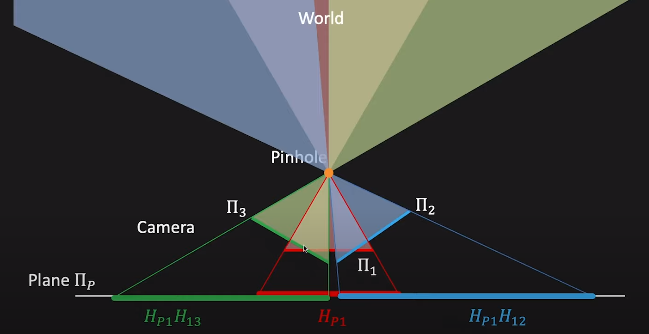
각 이미지는 central point를 기준으로, 각각의 Image Plane(π1,π2,π3)에 떨어집니다.
그리고 이들을 하나의 "평면 P"로 매핑하고 싶은 것 입니다.
(이 평면 P는 모든 다른 이미지 평면과 동일한 central point를 공유한다고 가정)
여기서 Homography의 역할이 나옵니다!
Homography?
"호모그래피"는 이러한 이미지 평면 간의 변환 매트릭스입니다.
이 행렬을 사용하면 이미지를 원하는 방식으로 변환하고 조합할 수 있고, 그렇기에 파노라마 이미지를 만들거나 확장된 시야를 제공하는 등의 작업을 수행할 수 있습니다.
Image mapping
1) 첫 번째 이미지는 "평면 1"에서 "평면 P"로의 Homography H1p를 사용하여 매핑됩니다.
2) 두 번째 이미지는 "평면 2"에서 "평면 1"로의 Homography H2,1을 사용하여 "평면 1"로 먼저 매핑되고, 그 다음에는 H1p를 사용하여 "평면 P"로 매핑됩니다.
3) 세 번째 이미지도 비슷한 방식으로 "평면 3"에서 "평면 1"로의 호모그래피를 사용하여 "평면 1"로 매핑하고, 다시 H1p를 사용하여 "평면 P"로 매핑됩니다.
Central Projection
중요한 점은 모든 이미지가 "동일한 central point"를 공유한다는 것입니다. 쉽게 말해, 카메라가 동일한 지점에서 서로 다른 방향으로 회전하지 않았다는 가정입니다. 이것이 호모그래피를 사용하여 다른 이미지 평면 간에 매핑할 수 있는 이유입니다.
모든 이미지를 단일 Plane P로 매핑
이 과정을 통해 우리는 서로 다른 이미지 평면에 있는 모든 이미지를 단일한 "평면 P"로 매핑할 수 있습니다. 이러한 방식으로, 호모그래피를 이용하여 서로 다른 이미지 간에 변환이 가능하고, 이것은 이미지 스티칭과 같은 작업에서 중요한 역할을 합니다. 여러 이미지를 조합하여 더 큰 이미지나 파노라마를 만들 때, 호모그래피를 통해 이미지들을 원하는 평면에 정확하게 정렬할 수 있습니다.
Q. 과정은 이해했는데, 왜 굳이 Plane 1에 mapping한 후 Plane P로 mapping할까?
결론부터 말해면, 이미지 2를 먼저 평면 1로 매핑하고, 그런 다음 평면 1을 평면 P로 매핑함으로써, 이미지 2의 왜곡 및 카메라의 위치와 방향 정보를 보존할 수 있기 때문입니다!
먼저 이미지 2를 평면 1로 매핑하면 이미지 2를 이미지 1과 동일한 좌표 공간으로 옮길 수 있습니다. 이렇게 이미지 1과 이미지 2는 동일한 좌표 공간에서 정렬되고, 이를 평면 P로 이동하게 되면 왜곡이 더 적게 발생합니다.
즉, 카메라의 위치와 방향 정보를 고려하고, 이미지를 먼저 중간 평면(평면 1)으로 매핑한 다음 평면 1에서 평면 P로 매핑함으로써 왜곡 보존과 이미지의 정확한 정렬을 가능하게 하는 것이 더 효과적입니다!
2. Computing Homography
이제 실질적으로 호모그래피를 계산하는 과정을 알아보겠습니다.
아래와 같이 두 개의 이미지(Source Image & Desination Image)가 있을 때, 두 이미지의 특징을 일치시키는 점을 가장 잘 정렬하는 최적의 homography H를 찾는 것이 목표입니다.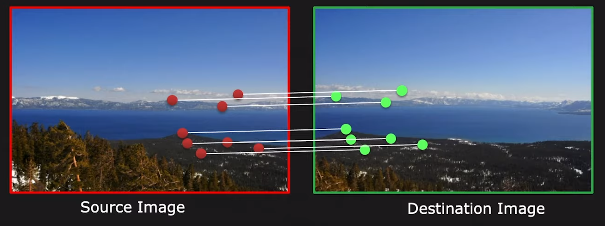
식을 살펴보면 Source Image의 point [xs, ys, 1]을 Destination Image의 [xd, yd, 1]로 연결짓고 싶은 것 입니다.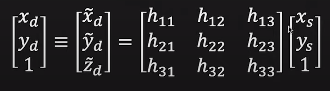
Q. How many unknowns?
이제 이 시스템을 풀어서 H를 구하려고 하는데, H는 스케일 계수가 있기에 8개의 파라미터를 가지고 있다는 점에 유의하는 것이 중요합니다.
Q. How many minimum pairs of matching points?
H를 안정적으로 추정하려면 일반적으로 일치하는 쌍을 4개 이상 사용하는 것이 좋습니다.
계산을 살펴보면 아래와 같이 표현할 수 있습니다.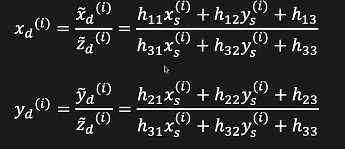
이를 정리하면 아래와 같고, Known과 unKnown을 구별하여 결국 구하고자 하는 식은 Ah=0으로 최종적인 목표를 구할 수 있게 됩니다.(||h||=1)
이 식을 least squares로 풀어 내어 min||Ah||^2 st ||h||=1을 수행하면 되는 것 입니다! 여기서 ||Ah||^2=(Ah)T(Ah)=hTATAh 이기에 Loss ft을 아래와 같이 정의하게 됩니다.
loss ft의 minimum을 구하기 위해 미분을 수행하면 이와 같은 식을 얻을 수 있으며, 이는 결국 Eigenvalue Problem을 푸는 것과 같이 됩니다!
즉, Eigenvalue로 넘어온 순간 Eigenvector h with smallest eigenvalue λ of matrix ATA가 loss ft을 최소화하는 것 입니다.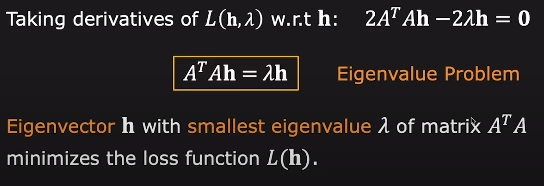
이제 전체 상세한 흐름을 살펴보겠습니다.
1) 각 이미지에 SIFT(Scale-Invariant Feature Transform) 기능 검출기를 적용하여 특징점을 찾습니다.
2) 이 두 이미지 사이에서 매칭되는 특징점을 찾습니다.
최소한 네 개의 매칭 특징점이 필요하지만, 보통 더 많은 매칭 페어를 사용하여 호모그래피 추정을 더 견고하게 만듭니다.3) 모든 매칭 페어의 좌표를 사용하여 호모그래피 계산에 사용할 수 있는 큰 행렬 A를 만듭니다.
4) 행렬 A의 특이값 분해(SVD)를 수행하여 A의 가장 작은 특이값에 해당하는 특이벡터를 찾습니다. 이것이 우리가 찾는 호모그래피 행렬입니다!
5) 찾은 호모그래피 행렬의 요소를 재배열하여 3x3 행렬로 변환하고 이를 사용하여 이미지를 원하는 대상 이미지 평면에 매핑할 수 있습니다.
참고 : https://www.youtube.com/watch?v=l_qjO4cM74o&list=PL2zRqk16wsdp8KbDfHKvPYNGF2L-zQASc&index=4
