Image Stitching - Geometric Image Transformations: Understanding 2x2 Matrix Transformations

이번 포스터에서는 image stitching의 기하학적 이미지 변환 중 2x2 matrix transformation을 중심으로 image manipulation에 대해 작성하겠습니다.

1. Image Manipulation Categories

크게 두 가지 카테고리가 있습니다.

첫 번째로는 1) image filtering 입니다.
이것은 입력 이미지 f(x, y)와 출력 이미지 g(x, y)를 가지며 변환을 적용하지만 이미지의 범위나 밝기 및 색상만을 변경합니다. 그렇기에 이 경우 이미지의 밝기 값을 변환하여 이미지를 생성하며 이미지의 모양은 변경하지 않습니다.
예를 들어 픽셀 처리 및 합성 등의 기술이 이 범주에 속합니다.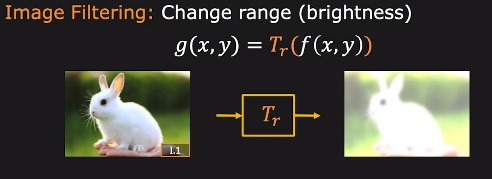

두 번째는 2) image warping 입니다.
이미지 왜곡이라고 하며, 이미지의 영역을 변형하여 이미지의 모양을 수정하는 것 입니다.

그렇기에 Tr(:range), Td(:domain) transformation이 있으며, 이렇게 두 가지를 기준으로 살펴보겠습니다.

2. Global Geometric Transformations

기하학적 변환으로는 이미지 전체에 일관되게 적용되며 일반적으로 몇 가지 매개변수로 설명할 수 있습니다.

1) 이동 : 이미지를 이동
2) 회전 : 이미지를 회전
3) 스케일링 : 이미지를 확대 or 축소
4) 아핀 변환 : 선과 평행성을 보존하는 (하지만 거리와 각은 반드시 그렇지는 않은) 기하 변환
5) 투영 변환 : 말 그대로 이미지를 투영시켜 변환
6) 기하학적 왜곡 : 영상의 좌표에 기하학적인 연산을 가해서 변환된 새로운 좌표를 얻는 것(위의 내용들이 포함되기는 합니다.)

3. 2x2 trasnformation

이번 포스터에서는 2x2 matrix만 다루기에 이 2x2행렬 변환을 살펴보겠습니다.

쉽게 말해 P1=(x1, y1)을 2x2 Transformation T에 의해 P2=(x2,y2)로 보내는 것 입니다.

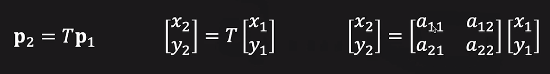
우선 스케일링(Stretching or Squishing)을 알아보겠습니다.
x1 -> ax1 = x2
y1 -> by1 = y2
로 보내고 싶은 것 입니다.
그렇기에 S = [[a, 0], [0, b]] 로 설정한 후 [x2, y2] = S[x1, y1] 으로 구할 수 있습니다. S matrix가 invertible하기에 다시 Inverse인 [[1/a, 0], [0, 1/b]]를 취해 복구시킬 수도 있습니다!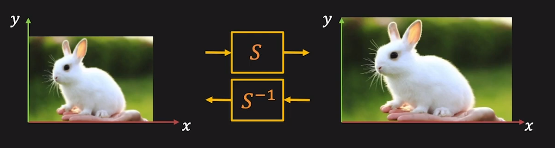

두 번째로 회전을 알아보겠습니다.
x1 = rcos(Φ), y1 = rsin(Φ) -> Θ만큼 rotate하여, x2 = rcos(Φ+Θ), y2 = rsin(Φ+Θ) 로 변경하고 싶은 것 입니다.

이 경우에는 R = [[cosΘ, -sinΘ], [sinΘ, cosΘ]] 로 설정할 수 있으며, inverse로 [[cosΘ, sinΘ], [-sinΘ, cosΘ]] 를 취해 구할 수 있습니다.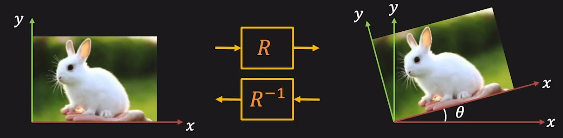

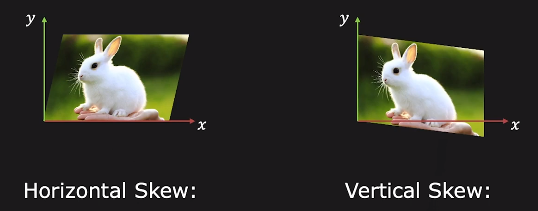
세 번째로 Skewing입니다.

Horizontal Skew는
x2 = x1 + mxy1
y2 = y1
즉, [[1, mx], [0, 1]] 을 통해 구할 수 있습니다.

Verical Skew도 마찬가지로
x2 = x1
y2 = myx1 + y1
[[1, 0], [mx, 1]]을 통해 구할 수 있습니다.

마지막으로 반사가 있습니다.

y축에 대해 mirror을 취하면
x2 = -x1
y2 = y1
[[-1, 0], [0, 1]] 을 통해 mirroring을 할 수 있습니다.

y=x에 대해서는
x2 = y1
y2 = x1
으로 [[0, 1], [1, 0]]을 통해 구할 수 있습니다.

이 2x2 matrix transformation은 중요 특성 몇 가지를 가지고 있습니다.

• 원점은 변환 후에도 원점에 매핑됩니다.
• 이미지의 선들은 변환 후에도 선으로 매핑됩니다.
• 이미지의 평행한 선들은 변환 후에도 평행하게 유지돕니다.
• 마지막으로 가장 중요한 특성으로, 합성의 폐쇄성입니다.
  즉, P1이 P2로 변환되고 P2가 P3로 변환되면 P1에서 P3로 직접 변환을 나타내는 변환 T13을 T23와 T12의 조합으로 표현할 수 있다는 점 입니다.

이렇게 image stitching에서의 2x2 geometric image transformation을 알아보았습니다. 다음 포스터에서는 3x3 matrix transformation을 알아보겠습니다.

참고 : https://www.youtube.com/watch?v=K2XLXlyPqCA&list=PL2zRqk16wsdp8KbDfHKvPYNGF2L-zQASc&index=2