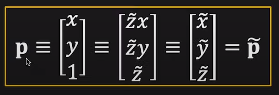Image Stitching - Geometric Image Transformations: Understanding 3x3 Matrix Transformations

이번 포스터에서는 image stitching의 기하학적 이미지 변환 중 3x3 matrix transformation과 Homogeneous 좌표에 대해 작성하겠습니다.

1. Translation

먼저 이미지를 x 방향으로 tx 만큼, y 방향으로 ty 만큼 이동시키는 것을 생각해 보겠습니다.
x2 = x1 + tx
y2 = y1 + ty
로 작성할 수 있는데, 이 부분은 2x2 transformation matrix로 표현하는데 한계가 존재합니다.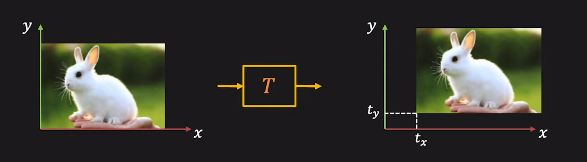

따라서 이를 극복하기 위해 하나의 차원을 추가시켜 2x2 transformation matrix를 사용합니다. 여기서 Homogeneous Coordiantes 내용이 나오게 됩니다.

2. Homogeneous Coordinates

이 Homogeneous 좌표는 2D point p(x, y)를 3D tilde point (xtilde, ytilde, ztilde) 로 확장하는 방법입니다.

여기서 표현되는 z tilde는 정규화를 위해 사용되는 가상좌표로, 3D에서 다시 2D로 갈 때는 x=xtilde/ztilde, y=ytilde/ztilde 로 표현됩니다.

Homogeneous Coordinates의 기하학적 의미?
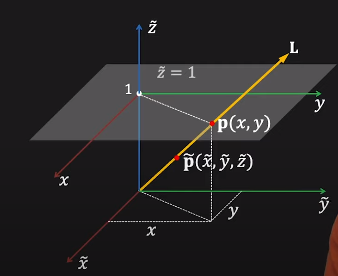
2차원 상에 있던 p(x, y)를 3차원으로 옮겨 z=1로 p(x, y, z=1) point를 생각해 봅니다.
여기서 p와 origin point가 이어지는 line L을 만듭니다. 이 L을 지나는 origin pt를 제외한 모든 point들이 Homogeneous Coordinates를 의미하는 것 입니다.
즉 이 p는 아래와 같이 나타낼 수 있고, 좌표가 어떻게 확장된 공간에서의 동일한 점을 나타내는 데 사용된다는 개념을 이해할 수 있습니다.

3. 3x3 translation matrix

위에서 살펴본 바와 같이 이제는 3차원으로 생각할 수 있게 됩니다.

아래와 같이 3x3행렬을 통해 초반에 언급한 한계점을 해결할 수 있습니다.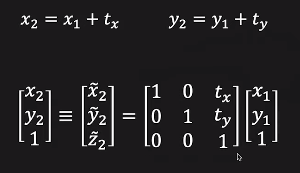

3x3 변환 행렬은 위에서 구한 바와 같은 단순한 이동만 가능한 것일까요?
=> 그렇지 않습니다. 우리가 2x2 변환 행렬로 할 수 있었던 모든 작업들은 물론, 3x3 변환 행렬을 사용해서도 수행할 수 있습니다.

• 확대/축소 (Scaling): 이미지의 크기를 변경하는 변환입니다. 처음에는 확대와 축소 중 일부를 사용했었습니다.

• 비틀기 (Skewing): 직사각형을 평행사변형으로 변환시키는 것입니다.

• 이동 (Translation): 이미지를 이동시키는 변환입니다.

• 회전 (Rotation): 이미지를 회전시키는 변환 등도 가능합니다.

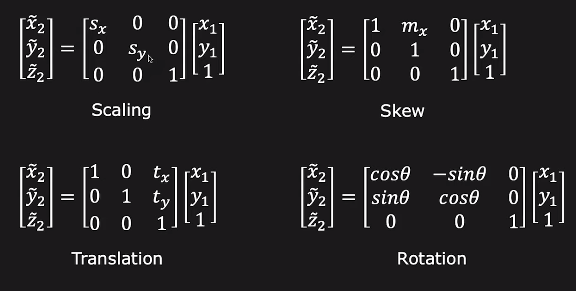
이미지를 비틀고, 그런 다음 이동하고, 크기를 조절하고, 회전시키려면 이러한 변환을 순차적으로 적용할 필요가 없습니다.

=> 다시 말해, 각 변환을 계산하고 그 변환들을 순서대로 곱하면, 단일 3x3 변환 행렬로 나타낼 수 있다는 것 입니다! 이렇게하여 원하는 순서대로 여러 변환을 한 번에 적용할 수 있습니다.

4. Affine Transformation

위에서 말한 모든 변환은 아핀 변환이라는 범주 안에 있으며, 아핀 변환의 일반적인 형태는 다음과 같습니다.

x1y1z1를 3x3 행렬과 곱하면 x2y2,1로 나타납니다. 여기서 특징은 3x3 행렬의 마지막 행은 항상 [0, 0, 1]로 구성되어 있습니다. 이것이 아핀 변환의 특징이며, 여기서는 총 6개의 매개변수가 있습니다.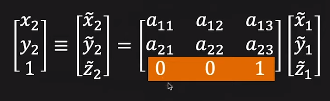

아핀 변환의 중요한 특징은 다음과 같습니다:

1) 원점은 반드시 원점으로 매핑되지 않을 수 있습니다.
이는 이미 이동이나 translation에 의해 원점이 이동되기 때문입니다.

2) 직선은 직선으로 매핑됩니다.
즉, 직선은 변환 후에도 직선으로 남습니다.

3) 평행한 직선은 평행을 유지합니다.
이미지에서 객체 간의 상대적인 위치와 각도를 유지하는 데 도움이 됩니다.

4) Closed under composition
즉, 아핀 변환들을 연속해서 적용할 수 있으며, 그 결과는 또 다른 아핀 변환이 됩니다.

5. Projective Transformation

Q. 만약 마지막 행을 [0, 0, 1]로 제한하지 않는다면 어떻게 될까요?

3x3 변환 행렬의 마지막 행을 제한하지 않고 임의로 정의할 수 있는 경우, 이것을 Projective matrix라고 부르며, homography라고 합니다.

이 Projective matrix는 한 평면을 다른 평면으로 매핑합니다.

여기서 특별한 점이 있습니다.
"모든 점은 평면에서 다른 평면으로 이동하지만 중요한 한 점을 통과합니다."
이것이 homography가 하는 일입니다.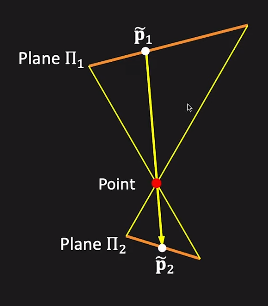

이것이 이미지 처리와 컴퓨터 비전 분야에서 중요한 이유입니다!

카메라는 평면을 pinhole을 통해 이미지로 매핑하는 것과 같은 projective transformation이라는 것을 의미합니다. 따라서 주어진 장면이 이미지 평면에 매핑될 때 이것은 호모그래피에 의해 주어진다는 것을 의미하게 됩니다.

추가적으로 projective transformation의 흥미로운 점은 homogeneous coordinates를 사용하기에 어떤 scalar를 곱해도 동등하다는 것 입니다.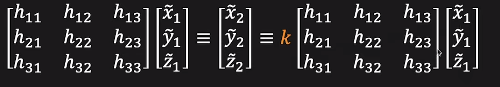

그렇기에 또한 하나의 파라미터 값을 1로 고정시킨다면 파라미터의 개수를 8개로 축소 시킬 수 있습니다.

마지막으로, Projective Transformation의 특징은 다음과 같습니다:

1) 원점이 반드시 원점으로 매핑되지 않습니다.

2) 직선은 직선으로 매핑됩니다.

3) 평행한 직선은 평행하지 않을 수 있습니다.

4) 변환은 합성 가능합니다.

특히, 평행한 직선이 평행하지 않게 되는 것이 중요한데, 이것이 소실점 (vanishing point)을 생성하는 원리입니다.

참고 : https://www.youtube.com/watch?v=B8kMB6Hv2eI&list=PL2zRqk16wsdp8KbDfHKvPYNGF2L-zQASc&index=3